Уравнение движения материальной точки
Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.
Имеет смысл говорить только о движении в некоторой системе отсчета.
Система отсчета. Системы координат
Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.
В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:
- сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
- цилиндрическая система с координатами p , z , α ;
- на полярной плоскости с параметрами r , φ .
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.
Кинематическое уравнение движения материальной точки
Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.
При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.
Это возможно при использовании кинематического уравнения движения:
Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.
Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:
x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .
Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.
Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.
Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:
r = r ( t ) , φ = φ ( t ) ( 3 ) .
Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как
q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .
Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.
Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:
Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.
Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.
Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.
Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.
Дано: x = 0 , 4 t 2 , t = 4 c
Найти: υ x ( t ) , S — ?
Решение
При решении необходимо учитывать зависимость скорости от времени:
υ x = υ 0 x + a x t .
Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:
x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .
Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .
После подстановки данных в уравнение:
Определим точки, изобразим график:
υ x = 0 , t = 0 , υ x = 4 , t = 5
Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:
Координатный способ задания движения точки
Рассматривается движение точки М в неподвижной системе отсчёта OXYZ (рис. 2.1). Единичные векторы (орты) i, j, k показывают положительные направления отсчёта координат X, Y, Z. Движущаяся точка описывает в пространстве некоторую линию, которую называют траекторией движения точки. По виду траектории все движения точки делятся на прямолинейные и криволинейные. Положение точки М в неподвижной системе отсчёта (НСО) определяется тремя координатами X, Y, Z. При движении точки М её координаты изменяются с течением времени. Следовательно, коорди 
наты X, Y, Z движущейся точки М являются функциями времени t.
Систему трёх уравнений X = f1(t); Y = f2(t); Z = f3(t) называют уравнениями движения точки в пространстве в декартовых координатах.

Пример: X = 10·t 2 + 1; Y = 7·t 3 + t 2 + 1; Z = 10·sin(p·t). Действительно, имея эти уравнения, можно для любого момента времени найти значения соответствующих координат X, Y, Z и по ним определить положение точки в пространстве в этот момент времени.
Движение точки М на плоскости (рис. 2.2) определяется двумя уравнениями: X = f1(t); Y = f2(t). Эти выражения называют уравнениями движения точки на плоскости в декартовой системе отсчёта.
Пример. Заданы уравнения движения точки в плоскости OXY. X = 3·t 2 + t 2 + t; Y = 7·cos(p·t).
Уравнения движения, определяющие координаты точки в любой момент времени, рассматривают как параметрические уравнения траектории точки. При исключении параметра t из уравнений движения получают уравнение траектории точки в координатной форме (Y = f(t)).

Пример. Заданы уравнения: X = 4·t (см); Y = 16·t 2 – 1 (см) движения точки в плоскости OXY. Определить вид траектории движения точки, построить её график и найти положение точки на траектории движения в момент времени t1 = 0,5 с.
Решение. Из уравнения X = 4·t находим t = X/4. Значение времени t подставляем в уравнение Y = 16·t 2 – 1. Получаем
Y = 16·(X/4) 2 – 1 = X 2 – 1.
Выражение Y = X 2 – 1 есть уравнение параболы (y= a·x 2 +b·x+c) с вершиной в точке с координатами (0, – 1). В момент времени t1 = 0,5 с определяем координаты:
Y(t1) = 16·(t1) 2 – 1 = 16·(0,5) 2 – 1 = 3 см >0.
Показываем положение точки на траектории её движения (рис. 2.3).
Пример. Дано: X = 3·sin(p·t), см (1); Y = 3·cos(p·t), см (2); t1 = 0,25 c. Определить вид траектории движения точки и её положение на траектории движения в момент времени t1.
Решение. Уравнения движения точки представим в следующем виде: (X) 2 = (3·sin(p·t)) 2 (1 I ); (Y) 2 = (3·cos(p·t)) 2 (2 I ). Для решения используем тригонометрическую формулу sin 2 (α) + cos 2 (α) = 1.
Складывая левые и правые части уравнений (1 I ) и (2 I ), получим (X) 2 + (Y) 2 = 3 2 ·(sin 2 (p·t) + cos 2 (p·t)) = 3 2 ·1 или (X) 2 + (Y) 2 = 3 2 . Известно, что уравнение (X) 2 + (Y) 2 = R 2 есть уравнение окружности радиусом R с центром в начале координат. Таким образом, точка 
движется по окружности радиусом R = 3 см (рис. 2.4).
Определяем положение точки на траектории движения в момент времени t1.
X(t1) = 3·sin(p·t1) = 3·sin(p·0,25) = 3·0,707 = 2,121 см > 0.
Y(t1) = 3·cos(p·t1) = 3·cos(p·0,25) = 3·0,707 = 2,121 см > 0.
Показываем точку на траектории её движения (см. рис. 2.4).
ВНИМАНИЕ! Если точка не попадает на траекторию её движения, то:
1) неверно определен вид траектории движения;
2) неверно рассчитаны значения координат X(t1), Y(t1).
Прямолинейное движение точки М определяется одним уравнением движения X = f(t).
Пример. Дано: X = 10·t 2 + sin(2·p·t) + 3, см (рис. 2.5).
Определить положение точки на траектории движения в начальный момент времени t0 = 0 и в момент времени t1 = 1 c.
Решение.
X(t0) = 10·(t0) 2 + sin(2·p·t0) + 3 = 10·0 2 + sin(2·p·0) + 3 = 3 см > 0.
X(t1) = 10·(t1) 2 + sin(2·p·t1) + 3 = 10·1 2 + sin(2·p·1) + 3 = 13 см > 0.
Значения координат X(t0), X(t1) наносим на рис. 2.5.
Динамика: Конспект лекций по курсу «Теоретическая механика» (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат)
Страницы работы
Содержание работы
для студентов II курса
Предлагаемый конспект лекций содержит только выборочные сведения из динамики. Многие понятия и теоремы не рассматриваются, а те, которые рассматриваются, приводятся без строгого доказательства или даже вообще без доказательства. Желающим познакомится более детально с положениями динамики, необходимо обратится к академическим учебникам. Термины, введенные в статике и кинематике, сохраняют свое значение и в динамике.
В настоящем конспекте материал изложен в том порядке и в том объеме, как он читается на лекциях в Воронежском филиале.
В конспекте принято обозначать определение терминов и основных понятий теоретической механики курсивом, причем сам термин пишется ЗАГЛАВНЫМИ буквами. В конце конспекта приводится отдельно список терминов и основных определений с указанием страницы, на которой приводится определение этого термина.
Когда формулируется какое-либо правило или рекомендация, которая имеет важное значение, они могут быть выделены ЗАГЛАВНЫМИ буквами.
Заголовки основных разделов выделены ЖИРНЫМИ ЗАГЛАВНЫМИ буквами, а заголовки подразделов ОБЫЧНЫМИ ЗАГЛАВНЫМИ или шрифтом с подчеркиванием. Также с подчеркиванием приведены слова «аксиома» и «теорема», когда они предшествуют формулировке. Сама формулировка приводится жирными строчными буквами.
В тексте встречаются ссылки на теоремы и аксиомы, рассмотренные ранее в статике или кинематике. В этом случае в ссылке присутствует заглавная буква, указывающая на раздел теоретической механики, в котором рассматривалась эта теорема или аксиома, а также ее порядковый номер в разделе. Иногда присутствует просто ссылка на раздел с указанием страницы, где был рассмотрен соответствующий вопрос.
Д И Н А М И К А
ДИНАМИКА изучает поведение материальных тел как результат их взаимодействия с другими телами.
Так как мерой взаимодействия является сила, то поведение сил и изменение характеристик движения во времени должны быть взаимосвязаны.
Все задачи динамики можно условно разделить на две категории:
— зная характеристики движения, определить силы, вызвавшие такое движение (ПРЯМАЯ ЗАДАЧА);
— зная силы, определить характеристики движения (ОБРАТНАЯ ЗАДАЧА).
При рассмотрении статики силы считались постоянными величинами, в динамике будем учитывать, что сила – величина переменная.
Аксиома Д1. Сила – это вектор.
Следовательно, с силами можно проделывать те же операции, что и с векторами, т.е. складывать, вычитать, проектировать, умножать на скаляр или другой вектор и т.д.
Аксиома Д2. Любое материальное тело можно представить как совокупность конечного числа материальных точек.
Аксиома Д3. Если силы, действующие на материальную точку, уравновешены или вовсе отсутствуют, то эта точка сохраняет состояние покоя или движется равномерно и прямолинейно (по инерции).
Движение равномерное и прямолинейное называется ИНЕРЦИОННЫМ ДВИЖЕНИЕМ.
Система координат, в которой выполняется аксиома Д1, называется ИНЕРЦИОННАЯ СИСТЕМА ОТСЧЕТА. Не все системы координат являются инерционными, поэтому чтобы пользоваться теоремами и законами динамики, необходимо побеспокоиться о правильном выборе системы координат. На практике следует учитывать, что безусловно инерционной можно считать только систему координат с центром в центре масс Солнца и осями, направленными на удаленные внегалактические объекты. Систему координат, располагающуюся на поверхности земли, можно считать инерционной весьма условно. При этом погрешность расчетов подавляющего большинства задач о движении тел вблизи поверхности Земли будет достаточно мала.
Аксиома Д4. Если на материальную точку действует сила, то эта точка будет двигаться с ускорением, прямо пропорциональным этой силе. Коэффициент пропорциональности между силой 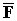
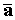
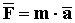
Поскольку в теоретической механике рассматриваются тела, движущиеся со скоростями только гораздо меньше скорости света, то МАССУ можно СЧИТАТЬ ПОСТОЯННОЙ ВЕЛИЧИНОЙ.
Возьмем две материальные точки с различными массами, например m1>m2, и подействуем на каждую из них одной и той же силой 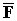
Видим, что чем больше масса точки, тем медленнее она будет двигаться под действием одной и той же силы при прочих равных условиях.
ИНЕРТНОСТЬ – это способность тел сопротивляться попыткам изменить их состояние.
МАССА ЯВЛЯЕТСЯ МЕРОЙ ИНЕРТНОСТИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛ. Чем больше масса, чет труднее привести тело в движение, но и труднее затем остановить его.
Аксиома Д5. Две материальные точки действуют друг на друга с силами равными по величине, лежащими на одной прямой и направленными в разные стороны (действие равно противодействию).
УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ
Рассмотрим движение материальной точки.
Пусть на нее действуют силы 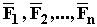
http://helpiks.org/3-65462.html
http://vunivere.ru/work98100