Уравнения эйлера пример вращение свободного тела

Динамические уравнения Эйлера

Динамические уравнения Эйлера

• Динамическое уравнение Эйлера для вращения объекта вокруг неподвижной точки под действием силы можно вывести из теоремы об изменении момента движения. Согласно этой теореме, dKoldt = L ^>, (10) Где Ko — момент движения тела относительно неподвижной точки от вращения тела относительно инерциальной системы отсчета. D> | = X — векторная сумма моментов Т внешней силы, действующей на тело (рис. 135). Среди внешних сил есть сила реакции в фиксированной точке.

Когда снаряд находится в движении, его центр тяжести движется так, как если бы в нем была сосредоточена вся масса тела и к нему были приложены все действующие на снаряд внешние силы. Людмила Фирмаль

Когда (10) представляется проекцией на инерциальную (фиксированную) координатную ось, моменты, которые меняются со временем, в зависимости от конкретного случая основных (3) и (4) главных осей, через Kx, Ku, K В том числе обычное уравнение инерции. Это расчет, который уже должен знать движение тела, и сам должен определяться силой, данной. Чтобы избежать этого, Эйлер предложил проецировать вектор (10) на движущуюся ось координат, прикрепленную к вращающемуся телу.

• Для таких осей момент инерции не зависит от времени. Подготовьте векторное уравнение (10) для проекции на оси подвижных координат, закрепленных на движущемся объекте. По этой причине абсолютная производная по времени от момента движения должна быть выражена как относительная производная по формуле Бора. + К. Болезнь.

Это связано с тем, что система перемещения осей координат имеет ту же угловую скорость, что и само тело, с которым эти оси связаны. Представлено векторное поколение для удобства проецирования Удалить вектор в виде определителя, затем развернуть до элементов первой строки, т.е. | J K I шхко = тсс шу юг = / (шу ^ 1-шхх) + | к * к, кг я + j (azKx-axKz) + H (axKy-ayKx), (12) где i, j и H — единичные векторы, ориентированные вдоль осей координат движущейся системы координат.

В разделе упражнений будет показано, что систему векторов можно всегда привести к таким двум векторам, из которых Ъдин лежит на произвольной прямой, не параллельной главному вектору. Людмила Фирмаль

Используйте уравнение (I) для выражения теоремы об изменении момента движения (10) в следующем виде: Рисунок 135 В проекции на ось подвижной координаты, прикрепленной к вращающемуся телу, с учетом (10 ‘) — (12), ^ + — (15) sog = f cos6 4-f, Это представляет проекцию угловой скорости вращения объекта на движущиеся координатные оси, прикрепленные к объекту через углы Эйлера f, 6, f и их производные по времени.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

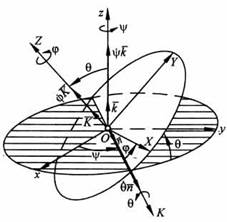
Вращение твердого тела вокруг неподвижной точки. Углы Эйлера

Движение твердого тела называетсявращением вокруг неподвижной точки, если во все время движения одна и та же точка твердого тела остается неподвижной. Вращение твердого тела вокруг неподвижной точки называют сферическим движением, поскольку траектория любой точки тела располагается на поверхности сферы с центром в неподвижной точке тела.

Положение тела, как правило, определяется углами Эйлера: углом прецессии , углом нутации , углом собственного вращения .

Линию OK пересечения координатных плоскостей Оху (на рис. изображена в виде заштрихованного овала) и OXY (ограничена белым овалом) назовем линией узлов. Тогда угол прецессии у определяет положение линии узлов ОК относительно неподвижной координатной оси Ох. Для изменения этого угла тело должно вращаться вокруг неподвижной оси Oz, называемой осью прецессии. Угол нутации определяет положение подвижной оси OZ относительно неподвижной Oz и равен углу между этими осями. Изменение угла сопровождается вращением тела вокруг линии узлов ОК, называемой осью нутации. Наконец, угол собственного вращения характеризует вращение тела вокруг оси OZ, называемой осью собственного вращения. В подвижной плоскости OXY это угол между линией узлов ОК и подвижной осью ОХ.

Положительное направление отсчета углов Эйлера , и противоположно направлению движения часовой стрелки, если смотреть на поворот тела с положительных направлений осей Oz, ОК и OZ соответственно.

Уравнения вращения твердого тела вокруг неподвижно точки: .

Скорости и ускорения точек тела при его вращении вокруг неподвижной точки.

Скорости и ускорения точек твердого тела при его свободном движении.

Переносное движение — поступательное движение вместе с полюсом. (Ve)

Относительное движение — вращательное движение относительно полюса. (Vr)

vM = dρ/dt = dr0/dt + dr/dt = v0 + ωr = (vM)e + (vM)r

a = dv/dt = dv0/dt + (dω/dt)*r + ω(dr/dt) = a0 + ε*r+ ω*r = a0 + a(вр) + а(ос) = (аМ)е + (аМ)r

(все что идет ниже, может не относиться к этому вопросу)

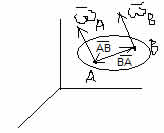
1) Полюс — т. А: vB = vA + ωS*AB

2) Полюс — т. В: vA = vB + ωB*BA = vB — ωB*AB

1) + 2) : (vB + vA) = (vA + vB) + ω*AB- ωB*AB

Сложное движение точки. Основные понятия.

Движение точки, исследуемое одновременно в основной и подвижной (подвижных) системах отсчета, называется сложным. В простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти движения.

Рассмотрим сложное движение точки M, перемещающейся по отношению к подвижной системе O’XYZ, связанной с некоторым телом Qy которое в свою очередь совершает свободное движение по отношению к основной, условно неподвижной системе Oxyz.

Движение точки М по отношению к неподвижной системе отсчета Oxyz называется абсолютным, или сложным, состоящим из относительного движения по отношению к подвижной системе O’XYZ и переносного — движения подвижной системы отсчета O’XYZ по отношению к неподвижной системе Oxyz.

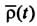
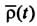
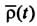
Положение точки М в подвижной системе координат O’XYZ характеризует радиус-вектор с началом в точке О’. Траектория точки М в подвижной системе отсчета называетсяотносительной траекторией и представляет собой годограф радиус-вектора . Скорость движения точки М по отношению к осям подвижной системы координат называетсяотносительной скоростью и обозначается Vr. Вектор Vr определяет скорость изменения с течением времени радиус-вектора в подвижной системе O’XYZ и поэтому выражается его относительной, или локальной, производной по времени, .
Ускорение точки М в этом движении называется относительным ускорением и обозначается аr. Вектор аr характеризует скорость изменения вектора относительной скорости Vr в подвижной системе O’XYZ и поэтому выражается относительной, или локальной, производной по времени от Vr: .

Движение подвижной системы O’XYZ по отношению к неподвижной Oxyz является для точки М переносным движением, а скорость и ускорение той неизменно связанной с подвижной
системой отсчета точки А, с которой в данный момент времени совпадает точка М, называют переносными скоростью и ускорением точки М и обозначают Ve и ае.

Переносные скорость и ускорение точки М определяются по формулам: , где вектора Vo’ и ao’ — скорость и ускорение точки О’ подвижной системы координат.