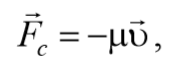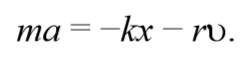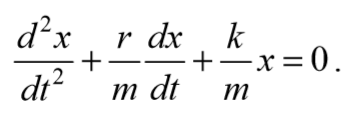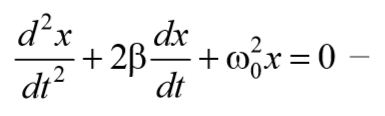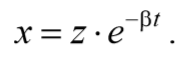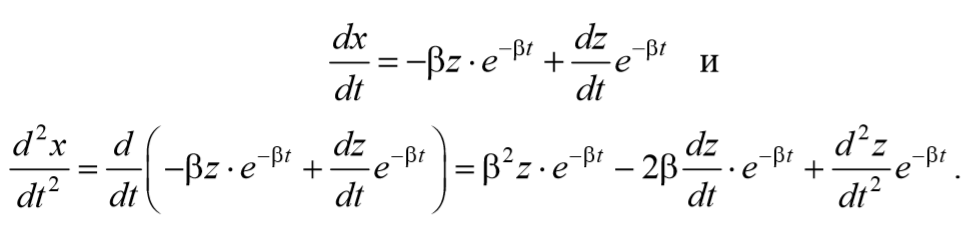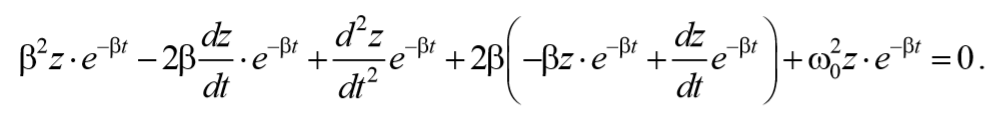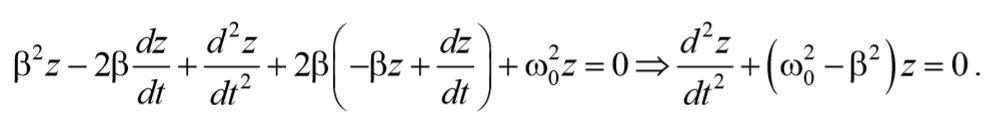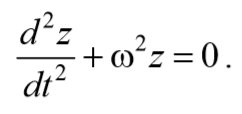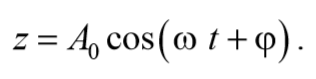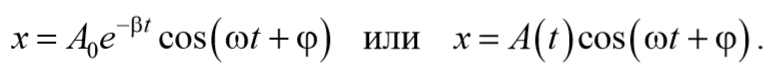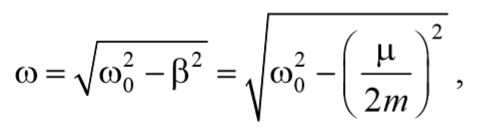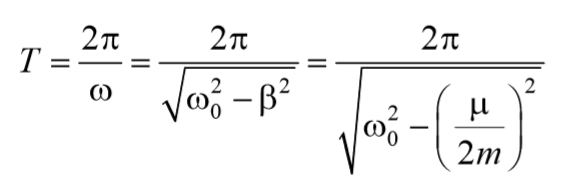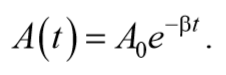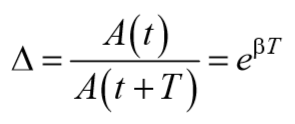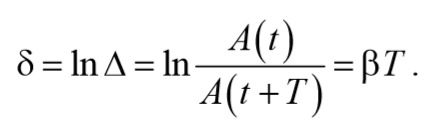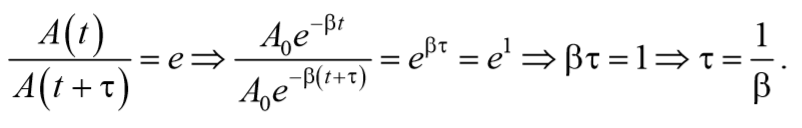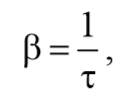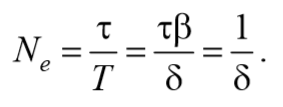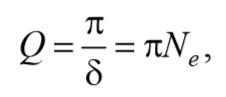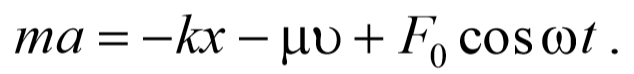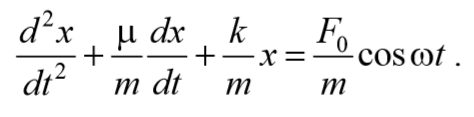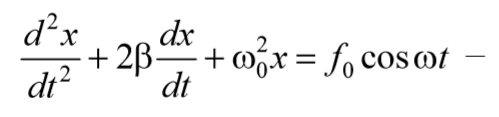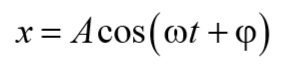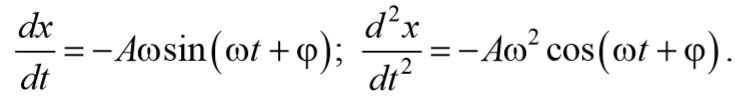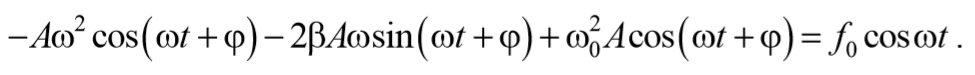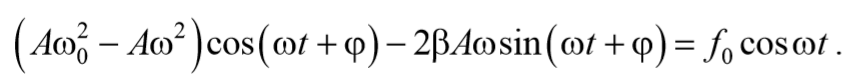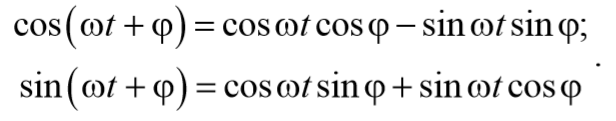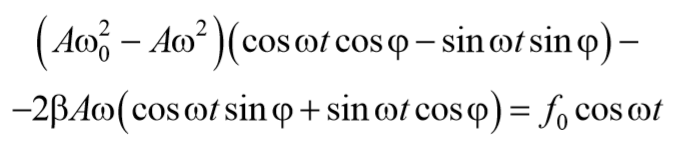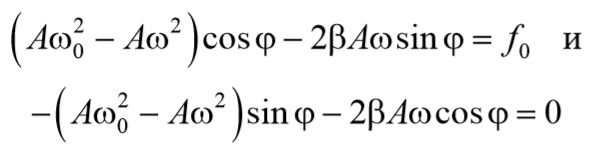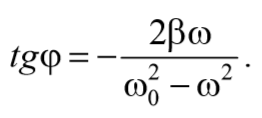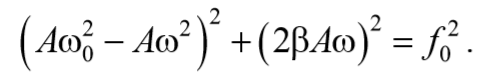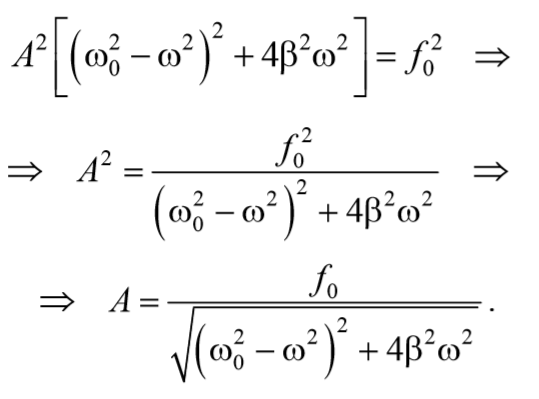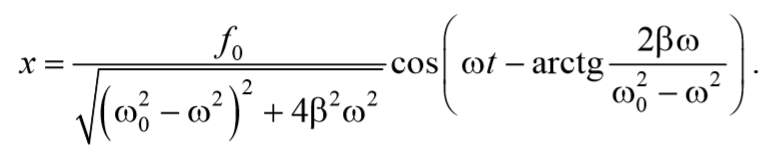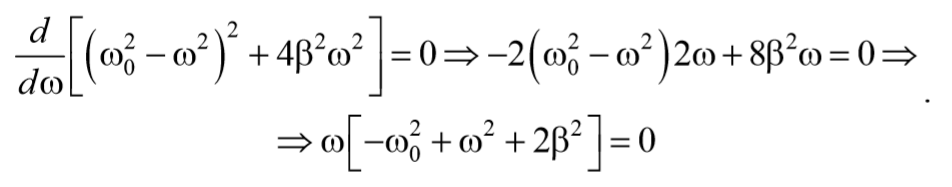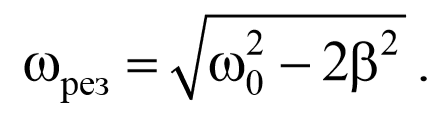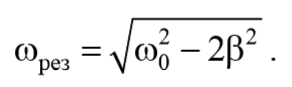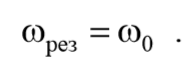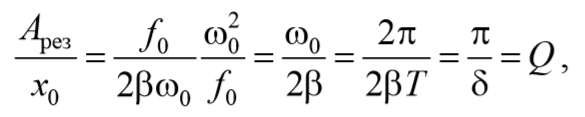Уравнения гармонических затухающих и вынужденных колебаний

Лекция №8. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.6. Затухающие гармонические колебания.

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающие колебания − это колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления, вызывающая затухание, зависит от скорости колебательного движения, т. е. ее можно считать прямо пропорциональной скорости

где μ − постоянная, называемая коэффициентом сопротивления.

Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления. Тогда второй закон Ньютона для гармонических колебаний при наличии сил сопротивления имеет вид

Учитывая , что a= $$d^2x\over dt^2$$ , а υ= $$dx\over dt$$ и разделив на массу m , получим

Применив обозначения $$ = ω_0<^2>$$ , $$ <μ\over m>= 2β$$ и $$ = f_0$$ получим

дифференциальное уравнение затухающих колебаний . Отметим, что ω₀ представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды. Эта частота называется собственной частотой .

Для решения уравнения (5.6.4) сделаем подстановку

Проведем замену переменных

Подставим (5.6.5 и 5.6.6) в выражение (5.6.4)

Преобразуем , сократив на e -βt

Рассмотрим случай, когда сопротивление среды настолько мало, что ω₀ 2 -β 2 >0 есть величина положи мы можем ввести тельная, и обозначение ω₀ 2 -β 2 =ω 2 , после чего уравнение (5.6.8) примает вид

В случае большого сопротивления среды ω₀ 2 -β 2 , движение становится непериодическим.

Решение уравнения (5.6.8) можно записать в виде

Окончательно, подставляя последнее уравнение в выражение (5.6.5), получаем общее решение дифференциального уравнения затухающих колебаний (5.6.4)

В соответствии с видом полученной функции движение можно рассматривать как гармоническое колебание с частотой

и амплитудой, изменяющейся по закону

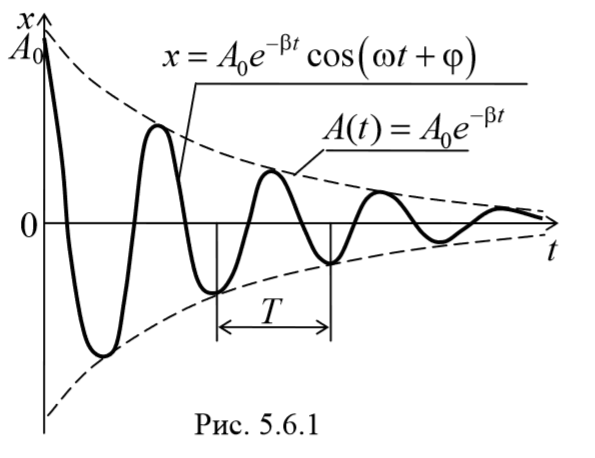
На рисунке показан график данной функции. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Верхняя из пунктирных кривых дает график функции A(t) , причем величина A₀ представляет собой амплитуду в начальный момент времени. Начальное смещение зависит от A₀ и также от начальной фазы φ , т.е. x₀=A₀cosφ .

5.7. Коэффициент затухания и логарифмический декремент затухания.

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно

и называется декрементом затухания .

Для характеристики системы обычно используется колебательной логарифмический декремент затухания , т.е. логарифм декремента затухания

Скорость затухания колебаний определяется величиной называем коэффициентом затухания $$β=<μ\over 2m>$$ .

Найдем время, называемое временем релаксации τ , за которое амплитуда уменьшается в e раз

т. е. коэффициент затухания обратен по величине промежутку времени, за который амплитуда колебаний уменьшается в e раз.

За время релаксации τ система успевает совершить $$N_e=<τ\over T>$$ колебаний

Следовательно, $$δ=<1\over N_e>$$ логарифмический декремент затухания обратно пропорционален по величине числу колебаний, за которые амплитуда колебаний уменьшается в e раз.

Для характеристики колебательной системы используется величина

которая называется добротностью колебательной системы.

Величина Q , пропорциональная числу колебаний, совершаемых системой за время, в течение которого амплитуда колебаний уменьшается в e раз.

5.8. Вынужденные колебания.

До сих пор мы рассматривали свободные колебания, когда выведенная из положения равновесия система совершает колебания будучи предоставленной самой себе. Рассмотрим колебательную систему, которая подвергается действию внешней силы, изменяющейся по гармоническому закону F=F₀cosωt . Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями . В этом случае уравнение второго закона Ньютона имеет вид

Учитывая , что a= $$d^2x\over dt^2$$ , а υ= $$dx\over dt$$ и разделив на массу m , получим

Применив обозначения $$ = ω_0<^2>$$ , $$ <μ\over m>= 2β$$ и $$ = f_0$$ получим

дифференциальное уравнение вынужденных колебаний.

Будем искать решение уравнения (5.8.3) в виде

предполагая, что результирующее колебание будет совершаться с частотой внешней вынуждающей силы.

Подставим (5.8.4) и (5.8.5) в уравнение (5.8.3)

Чтобы уравнение (69) обратилось в тождество необходимо, чтобы коэффициенты при cosωt и sinωt были равны нулю.

Из выражения (71) получаем

Возведем в квадрат уравнения (70) и сложим

Подставив полученные выражения (71) и (73) в выражение (64) получим уравнение вынужденных колебаний

5.9. Резонанс.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы называется резонансом , а соответствующая частота − резонансной частотой.

Найдем резонансную частоту. Амплитуда вынужденных колебаний будет max, когда выражение $$(ω_0<^2>-ω^2)^2 + 4β^2ω^2$$ в уравнении $$A=-ω^2)^2 + 4β^2ω^2>>$$ (5.8.13) будет минимальным.

Продифференцируем это выражение по ω и приравняем к нулю

Полученное уравнение имеет три решения: ω=0 и ω=± $$\sqrt <ω_0<^2>-2β^2>$$ . 2 . Первое решение соответствует максимуму знаменателя. Из остальных двух решений отрицательное не имеет физического смысла (частота не может быть отрицательной). Таким образом, резонансная циклическая частота

Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе

Из последнего уравнения (5.9.3) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при β=0 ), совпадала бы с собственной частотой колебаний системы ω₀

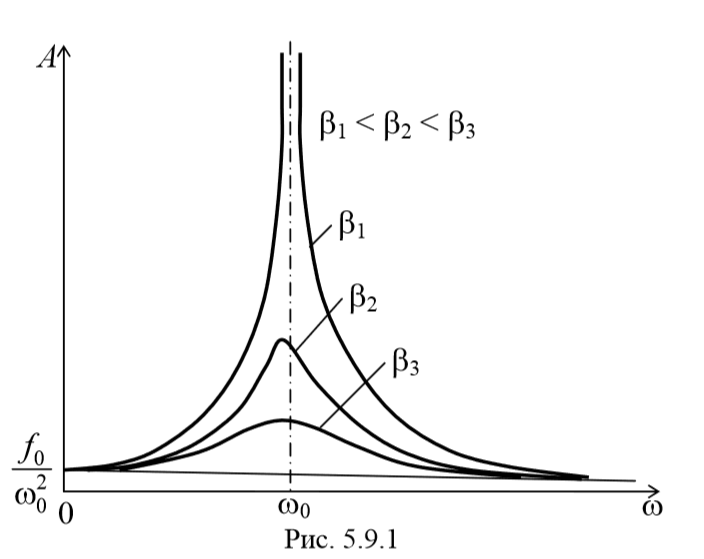
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 5.9.1. В соответствии с (5.9.2) и (5.9.3), чем меньше параметр β , тем выше и правее лежит максимум данной кривой. Изображенная на рис. 5.9.1 совокупность графиков функций (5.8.13), соответствующих различным значениям параметра β , называется резонансными кривыми .

При стремлении ω к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному f₀ω₀ 2 . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F₀

При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.

Наконец, отметим, что чем меньше β , тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум. При малом затухании (т. е. β ) амплитуда при резонансе приближенно равна A_pes≈f₀/2βω₀ . Разделим это выражение на смещение x₀ из положения равновесия под действием постоянной силы F₀ , равное x₀=f₀/ω_p 2 . В результате получим

где δ = βТ – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).

Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.

Гармоническое колебание. Уравнение. Автоколебания. Механический резонанс

Содержание:

Предмет:	Физика
Тип работы:	Реферат
Язык:	Русский
Дата добавления:	04.06.2019

Данный тип работы не является научным трудом, не является готовой работой!
Данный тип работы представляет собой готовый результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала при самостоятельной подготовки учебной работы.

Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!

По этой ссылке вы сможете найти много готовых тем для рефератов по физике:

Посмотрите похожие темы возможно они вам могут быть полезны:

Введение:

Механические колебания: гармонические, затухающие и вынужденные колебания Колебания называются процессами, которые отличаются различной степенью повторяемости (колебание маятника часов, колебания струны или ножки камертона, напряжение между пластинами конденсатора в радиосвязи, функция сердца).

В зависимости от физической природы повторяющегося процесса различаются колебания: механические, электромагнитные, электромеханические и т. Д. Будем рассматривать механические колебания. Колебания, происходящие в отсутствие трения и внешних сил, называются внутренними; их частота зависит только от свойств системы. Простейшими являются гармонические колебания, то есть такие колебания, в которых колеблющаяся величина (например, отклонение маятника) изменяется во времени в соответствии с законом синуса или косинуса.

Дифференциальное уравнение гармонического колебания

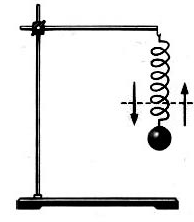
Рассмотрим простейшую колебательную систему: шар массы m подвешен на пружине. В этом случае сила упругости F1 уравновешивает силу тяжести mg. Если вы переместите шар на расстояние x, то на него будет действовать большая сила упругости (F1 + F). Изменение силы упругости в соответствии с законом Гука пропорционально изменению длины пружины или смещению шарика х: F = -kx, (1) где k — жесткость пружины. Знак «-» отражает тот факт, что смещение и сила имеют противоположные направления.

Сила F обладает следующими свойствами: она пропорциональна смещению шара из положения равновесия; оно всегда направлено в положение равновесия.

В нашем примере сила по своей природе эластична. Может случиться так, что сила другого происхождения обнаруживает один и тот же паттерн, то есть оказывается, что она равна — kx. Силы такого типа, неэластичные по своей природе, но сходные по свойствам с силами, возникающими при малых деформациях упругих тел, называются квазиупругими.

Поскольку k и m являются положительными величинами, их отношение может быть приравнено к квадрату определенного значения 0, то есть мы можем ввести обозначение.

Таким образом, движение шара под действием силы вида описывается линейным однородным дифференциальным уравнением второго порядка.

Подстановкой легко проверить, что решение уравнения имеет вид

где (0 t + 0) = — фаза колебаний; 0 — начальная фаза при t = 0; 0 — круговая частота колебаний; А это их амплитуда.

Итак, смещение x изменяется со временем в соответствии с законом косинуса.

Следовательно, движение системы под действием силы вида f = — kx является гармоническим колебанием.

Гармоническая Энергия

Выясним, как со временем меняются кинетическая Еk и потенциальная Еп энергия гармонического колебания. Кинетическая энергия равна:

Мы находим потенциальную энергию из формулы потенциальной энергии для упругой деформации и используя (3):

Сложив (4) и (5) с учетом соотношения, получим:

Таким образом, полная энергия гармонической вибрации остается постоянной в отсутствие сил трения, во время колебательного процесса кинетическая энергия переходит в потенциал и наоборот.

Затухающие колебания

Колебания, возникающие в системе в отсутствие внешних сил (но при наличии потерь на трение или излучение), называются свободными. Частота свободных колебаний зависит от свойств системы и интенсивности потерь.

Наличие трения приводит к затуханию колебаний. Колебания с уменьшающейся амплитудой называются затухающими.

Мы ограничимся рассмотрением малых колебаний, тогда скорость системы будет мала, а на низких скоростях сила сопротивления пропорциональна величине скорости:

где r — коэффициент сопротивления среды. Знак «-» связан с тем, что Ftr и V имеют противоположные направления.

Решение этого уравнения существенно зависит от знака разности: 2 = 02 -2, где — круговая частота затухающих колебаний.

Пунктирная линия показывает изменение амплитуды: A = A0e-t.

Период затухающих колебаний зависит от коэффициента трения и равен:

При небольшом сопротивлении среды (2 2) период практически равен. С увеличением коэффициента затухания период колебаний увеличивается.

Из формулы, выражающей закон уменьшения амплитуды колебаний, мы можем убедиться, что отношение амплитуд, отделенных друг от друга интервалом в один период (T), остается постоянным на протяжении всего процесса затухания. Действительно, амплитуды колебаний, разделенные интервалом в один период.

Это соотношение называется декрементом затухания.

Величина натурального логарифма часто принимается за меру затухания.

Это значение называется логарифмическим декрементом ослабления за период.

При сильном затухании 2> 02 из формулы следует, что период колебаний является мнимой величиной. Движение в этом случае имеет апериодический (непериодический) характер — система, выведенная из положения равновесия, возвращается в положение равновесия без колебаний. Какой из этих методов система приходит в равновесие, зависит от начальных условий.

Вынужденные вибрации. Резонанс

Вынужденные колебания — это те, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (силы воздействия). Пусть движущая сила изменяется со временем по гармоническому закону: f = F0 cos t, где F0 — амплитуда, круговая частота движущей силы.

При составлении уравнения движения необходимо учитывать, помимо движущей силы, также те силы, которые действуют в системе при свободных колебаниях, то есть квазиупругую силу и силу сопротивления среды.

Разделив это уравнение на m и переместив члены из dx и d2x в левую сторону, мы получим неравномерное линейное дифференциальное уравнение второго порядка:

где коэффициент ослабления, собственная частота системы.

Явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты движущей силы к собственной частоте колеблющегося тела называется резонансом, колебания, возникающие в этом случае, являются резонансными, а их частота называется резонансным колебанием.

Автоколебания

Системы, которые автоматически регулируют подачу энергии от внешнего источника, называются автоколебательными, а происходящие в них непрерывные периодические процессы называются автоколебаниями. Такими системами являются часы, электрический звонок, ламповый генератор электромагнитных волн и т. Д.

Разложение колебаний в гармонический спектр. Использование гармонического анализа для обработки диагностических данных

Сложение гармонических колебаний, направленных вдоль одной прямой.

Есть случаи, когда тело вовлечено одновременно в несколько колебаний, происходящих вдоль одного и того же или вдоль разных направлений.

Рассмотрим сложение двух гармонических колебаний одного и того же направления, одинаковой частоты и с одинаковыми амплитудами, но с разными начальными фазами 01 и 02. Смещение x колеблющегося тела будет суммой смещений x1 и x2:

x = x1 + x2 = Acos (0t + 01) + Acos (0t + 02).

Используя формулу, известную из тригонометрии для суммы косинусов двух углов, имеем:

то есть получается гармоническое колебание той же частоты с начальной фазой и амплитудой Ares.

Как видно, амплитуда Ares результирующего колебания зависит от разности фаз добавленных колебаний.

Рассмотрим два крайних случая:

Колебания происходят в фазе, то есть 01 = 02, а затем и Ares = 2A.

Если амплитуды не равны, Arez = A1 + A2.

Колебания происходят в противофазе, то есть 01 = 02, затем. Следовательно, Ares = 0. Если амплитуды не равны, например, A1> A2, то Ares = A1 — A2.

Таким образом, при сложении двух одинаково направленных гармонических колебаний одного и того же периода и с одинаковыми амплитудами получается гармоническое колебание одного и того же периода с амплитудой, которое в зависимости от соотношения фаз добавленных колебаний может изменяться от двойного значение, если колебания происходят по фазе до нуля, если они находятся в противофазе.

При сложении гармонических колебаний с разными частотами результирующее колебание не будет гармоническим, а будет сложным.

Начальные колебания.
Результирующие колебания.

Комплексное колебание и его гармонический спектр

Согласно теореме Фурье любое сложное колебание может быть представлено как сумма простых (гармонических) колебаний (гармоник), периоды или частоты которых кратны основному периоду или частоте сложного колебания.

Множество простых колебаний, в которые можно разложить это сложное колебание, называется его гармоническим спектром.

В гармоническом спектре сложного колебания указаны частоты и амплитуды всех его простых колебаний. Обычно спектр представлен в виде графика, на горизонтальной оси которого нанесены частоты; затем для каждой из частот простых колебаний, имеющихся в спектре, создается ордината, соответствующая амплитуде этого колебания. Если гармонический спектр сложной вибрации содержит лишь небольшое количество простых колебаний, а его график состоит из отдельных ординат, то такой спектр называется линейчатым спектром.

Если спектр содержит простые колебания почти всех частот в определенных пределах, то он называется сплошным и его график строится в виде непрерывной огибающей кривой.

Установление гармонического спектра является основным методом анализа сложных колебаний. Этот анализ проводится с использованием специальных инструментов — анализаторов гармоник. Они также используются в медицине при исследовании, например, колебаний биопотенциалов головного мозга и т. д. Многие процессы человеческого организма носят периодический характер: сердечные сокращения, дыхание, наполнение кровеносных сосудов и т. Д.

Сложение взаимно перпендикулярных вибраций

В результате сложения двух взаимно перпендикулярных колебаний другого периода тело движется по сложным фигурам, форма которых зависит от соотношения периодов, амплитуд и начальных фаз добавленных колебаний и которые называются фигурами Лиссажу.

Механические волны, их виды и скорость распространения

Колебательная система может отдавать энергию во внутреннюю среду. Эта передача энергии становится возможной благодаря тому, что частицы самой среды представляют собой миниатюрные колебательные системы. Молекулы среды связаны между собой силами, законы которых в определенных границах подобны законам сил упругости. Если одна из частиц оказывается удаленной из положения равновесия, то силы, действующие на нее со стороны соседних частиц, заставляют ее снова вернуться в устойчивое положение. Однако, согласно закону равенства действия и реакции, соседние частицы также будут подвержены действию смещающих сил и, в свою очередь, будут удалены из стабильного положения. Таким образом, каждое возмущение, однажды возникшее в определенной части среды, будет постепенно распространяться, захватывая частицы все дальше и дальше от места начального возмущения.

Колебательный процесс, обусловленный взаимодействием частиц, будет распространяться в среде с определенной конечной скоростью. Процесс распространения колебаний в среде называется волновым движением или просто волной. Для нашего случая это будет упругая или механическая волна.

Различают продольные и поперечные волны. Форма распространяющихся в среде волн существенно зависит от упругих свойств среды.

Волна, распространяющаяся в том же направлении, в котором происходят колебания частиц среды, называется продольной волной.

Продольные волны генерируются в телах с объемной эластичностью, то есть противодействуют объемной деформации сжатия. Это характерно для всех тел, поэтому они образуются в любой среде: твердой, жидкой, газообразной. Продольные волны, в частности, включают в себя звук, инфразвук и ультразвук.

Волна, в которой колебательное движение перпендикулярно направлению распространения колебаний, называется поперечной.

Поперечные упругие волны образуются только в твердых телах, которые имеют упругую форму, то есть сдвиговые деформации (например, сейсмические волны в земной коре во время землетрясений; волны, движущиеся вдоль растянутой струны; крутильные волны, вызванные попеременно скручиванием и раскручиванием конца длинной стержень) противодействовать сдвиговым деформациям.

Продольные и поперечные колебания частиц среды, несущей волну, являются частными случаями волнового процесса. Существуют и другие волны, в которых колебательные движения состоят из одновременных продольных и поперечных смещений. Это набухающие волны, поверхность.

Волновое уравнение

Рассмотрим поперечную волну. В поперечной волне частицы среды не сдвигаются в направлении распространения волны. Но колебания каждой последующей частицы среды запаздывают по фазе относительно предыдущих частиц. В результате гребни и впадины волны, видимые глазу, движутся в направлении распространения волны. Это наблюдается наблюдателем как движение волны.

Под скоростью волны понимают скорость, с которой одинаковые фазы колебаний частиц движутся в среде. Эта скорость называется фазовой скоростью волны. Скорость волны зависит от упругих свойств (а также плотности) среды.

Расстояние между двумя ближайшими точками среды, колебания которых происходят в одной и той же фазе, называется длиной волны или расстоянием, на которое колебания в среде распространяются за время, равное одному периоду колебаний. Он численно равен произведению скорости V распространения волны на период T или отношению скорости распространения волны к частоте колебаний:

Поскольку скорость распространения волны зависит от свойств среды, длина волны при переходе волны из одной среды в другую изменяется, хотя частота колебаний остается неизменной.

Кроме того, при колебаниях A или T волна характеризуется формой колебаний частиц в волне. Как и вибрации, волны делятся на простые (гармонические) и сложные.

Колебания, возбужденные в одной точке в однородной изотропной среде, распространяются от нее равномерно во всех направлениях, такая волна называется сферической. Если источник колебаний имеет значительную плоскую поверхность, то волна от него будет распространяться в направленном потоке, перпендикулярном поверхности источника; такая волна называется плоскостью.

Составляем уравнение плоской гармонической волны, которое позволяет определить смещение S точки B среды на любом расстоянии x от начальной точки A в направлении распространения волны в любое время. Пусть для начальной точки A уравнение колебаний: SA = A стоимость.

Точка B колеблется с фазовой задержкой на угол 0 = t0, соответствующий временному интервалу t, в течение которого волна проходит расстояние x между точками A и B. Тогда для точки B уравнение колебаний будет иметь вид:

SB = A cos (t — 0) = A cos (t — t0) = A cos (t — t0)

Подставляя значение t0 =, где V — скорость распространения волны, получаем:

Заменив в уравнении V = и = 2, тогда:

Таким образом, смещение точек S среды в упругой волне является функцией двух переменных: времени t и расстояния x точки от центра возбуждения колебаний, то есть S = f1 (x, t) ,

Если выбрать определенный момент времени (t1 = const), то уравнение дает зависимость смещения от расстояния x: St = f2 (x), то есть величину смещений точек среды вдоль направление х в данный момент времени t1. График этой зависимости (как снимок волны) называется волновым графиком. Для простой (гармонической) волны график имеет форму синусоидальной волны или волны косинуса.

Связь между смещением S точки, ее координатой x и временем t, выраженная в дифференциальной форме, называется волновым уравнением.

Чтобы составить уравнение плоской волны, находим частные производные второго порядка смещения S по времени t и координате x:

Таким образом, вторая производная временного смещения пропорциональна второй производной координатного смещения. Коэффициент пропорциональности равен квадрату скорости распространения волны V. Это дифференциальное уравнение плоской волны, распространяющейся в направлении оси x со скоростью V (см. Формулу 17). Он в наиболее общем виде описывает распространение волнового процесса.

Основные характеристики (амплитуда, период или частота, длина волны и форма волны) продольной волны, ее уравнение и графика аналогичны поперечной.

Энергетические характеристики волны

Гармонический спектр механических колебаний

Во время движения волны происходит передача энергии, которая состоит из кинетической и потенциальной энергий вибрирующих частиц среды. Более того, потенциальная энергия обусловлена деформацией вещества при взаимном смещении частиц. В отличие от колебаний свободного тела в волне, нет взаимного перехода кинетической и потенциальной энергии частиц. Мгновенные значения одной и другой энергии изменяются одновременно (по фазе) в соответствии с изменением смещения частиц.

Мгновенные значения энергии каждой частицы среды изменяются во времени с удвоенной частотой колебаний, и в каждый момент времени эти значения для разных частиц различны. Однако среднее значение энергии за период колебаний для всех частиц одинаково и составляет.

Значение, численно равное средней энергии Esr, передаваемой волной в единицу времени t через заданную поверхность S, перпендикулярную направлению распространения волны, называется потоком энергии через эту поверхность и измеряется в единицах мощности — Вт.

Поток энергии на единицу поверхности называется плотностью потока энергии и измеряется в Вт / м2. Плотность потока энергии также называется интенсивностью волны.

Плотность потока энергии, переносимого волной, можно рассматривать как вектор, совпадающий по направлению с вектором скорости волны.

Вектор, показывающий направление распространения волны и равный потоку энергии, проходящему через единичную область, перпендикулярную этому направлению, называется вектором Умова.

Вектор Умова для упругой волны зависит от плотности среды, квадрата амплитуды колебаний частицы, квадрата частоты колебаний и скорости распространения волны.

Николай Алексеевич Умов (1846–1915) — исследователь потока энергии. Идеи о движении энергии были изложены в его диссертации «Уравнения движения энергии в телах», которую он защищал в 1874 году на физико-математическом факультете Московского университета. И только спустя десять лет английский физик Пойнтинг пришел к тем же выводам о движении энергии. Имя Умова вошло в историю физики

Энергетические характеристики волны

Гармонический спектр механических колебаний

Из формулы следует, что мгновенные значения энергии каждой частицы среды изменяются во времени с удвоенной частотой колебаний, и в каждый момент времени эти значения для разных частиц различны.

Заключение

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Механические колебания

теория по физике 🧲 колебания и волны

Колебательное движение очень распространено. Заставить колебаться можно любое тело, если приложить к нему силу — однократно или постоянно. К примеру, если подтолкнуть качели, они начнут качаться вперед-назад, и такое движение будет приблизительно повторяться до тех пор, пока качели полностью не остановятся.

Другой пример колебательного движения — тело, подвешенное к пружине. Если его потянуть вниз и отпустить, то за счет сил упругости оно сначала поднимется вверх, а затем снова опустится вниз, затем движения вверх-вниз будут повторяться. Со временем они прекратятся под действием силы сопротивления воздуха.

Колебаниями можно назвать даже движение гири, которую поднимается тяжелоатлет вверх, а затем опускает в низ. При этом он будет прикладывать к гире силу постоянно. Гиря будет колебаться до тех пор, пока к нему будет прикладываться эта сила.

Колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.

Механические колебания — это колебательные движения, совершаемые физическим телом в механической системе.

Механическая система — совокупность материальных точек (тел), движения которых взаимосвязаны между собой.

Какими бывают колебания?

Напомним, что в механической системе выделяют два вида сил:

Внутренние силы — это силы, которые возникают между телами внутри системы. Примером внутренних сил служат силы тяготения между телами солнечной системы.
Внешние силы — силы, которые действуют на тела системы со стороны тел, которые в эту систему не входят. Примером внешней силы может стать сила ветра, под действием которой шарик, подвешенный к опоре за нить, отклоняется в сторону порыва ветра.

Свободные колебания

Свободные колебания — колебания, происходящие в системе под действием внутренних сил после того, как эта система выведена из положения равновесия.

Колебательная система — механическая система, в которой возможно совершение свободных колебаний.

Свободные колебания в колебательной системе могут возникнуть только при наличии двух условий:

После выведения из равновесия в колебательной системе появляются силы, направленные в сторону положения равновесия. Эти силы стремятся возвратить систему в положение равновесия.
Трение между телами колебательной системы относительно мало. В противном случае колебания либо сразу затухнут, либо не начнутся совсем.

Примеры свободных колебаний:

колебания шарика на дне сферической чаши;
движение качелей после однократного толчка;
колебания груза на пружине после ее растяжения;
колебания струны после ее отклонения.

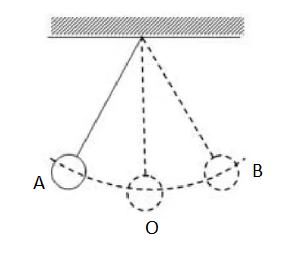
Примером колебательной системы также служит математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити. В действительности такого маятника не существует. Это идеализированная модель реального маятника, примером которого служит тяжелый шарик, подвешенный на длинной нити. В этом случае размером шарика и растяжением нити можно пренебречь.

В колебательную систему математического маятника входят:

нить;
тело, привязанное к нити;
Земля, в поле тяжести которой находится привязанное к нити тело.

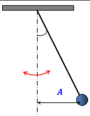
В положении равновесия (точка О) шарик висит на нити и покоится. Если его отклонить от положения равновесия до точки А и отпустить, под действием силы тяжести шарик приблизится к положению равновесия. Так как к этому моменту шарик обретет скорость, он не сможет остановиться и приблизится к точке В. Затем он снова вернется в точку А через положение равновесия в точке О. Шарик будет колебаться, пока не затухнут под действием возникающей силы сопротивления воздуха.

Вынужденные колебания

Вынужденные колебания — колебания тел под действием внешних периодически изменяющихся сил.

Примерами вынужденных колебаний служат:

движение поршня в цилиндре;
раскачивание ветки дерева на ветру;
движение иглы швейной машинки;
движение качелей под действием постоянных толчков.

Затухающие и незатухающие колебания

Затухающие колебания — колебания, которые со временем затухают. При этом максимальное отклонение тела от положения равновесия с течением времени уменьшается.

Колебания затухают под действием сил, препятствующих колебательному движению. Так, шарик в сферической чаше перестает колебаться под действием силы трения. Математический маятник и качели перестают совершать колебательные движения за счет силы сопротивления воздуха.

Все свободные колебания являются затухающими, так как всегда присутствует трение или сопротивление среды.

Незатухающими колебаниями могут быть только те, которые совершаются под действием периодической внешней силы (вынужденные колебания). Так, ветка будет раскачиваться до тех пор, пока дует ветер. Когда он перестанет дуть, колебания ветки со временем затухнут. Иголка швейной машинки будет совершать колебательные движения до тех пор, пока швея вращает ручку привода. Когда она перестанет это делать, иголка сразу остановится.

Динамика колебательного движения

Для того чтобы описать количественно колебания тела пол действием силы упругости пружины или колебания шарика, подвешенного на нити, воспользуемся законами механики Ньютона.

Уравнение движения тела, колеблющегося под действием сил упругости

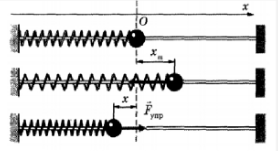
Рассмотрим колебательное движение шарика, вызванное силой упругости, возникшей при растяжении горизонтальной пружины вдоль оси Ох.

Согласно II закону Ньютона произведение массы тела на ускорение равно равнодействующей всех сил приложенных к телу. Поскольку сила трения пренебрежимо мала, мы можем считать, что в этой механической системе действует единственная сила — сила упругости. Учтем, что шарик колеблется вдоль одной прямой, и выберем одномерную систему координат Ох. Тогда:

m a x = F x у п р

Согласно закону Гука, проекция сила упругости прямо пропорциональная смещению шарика из положения равновесия (точки О). Смещение равно координате x шарика, причем проекция силы и координаты имеют разные знаки. Это связано с тем, что сила упругости всегда направлена к точке равновесия, в то время как расстояние от этой точки во время движения увеличивается в обратную сторону. Отсюда делаем вывод, что сила упругости равна:

F x у п р = − k x

где k — жесткость пружины.

Тогда уравнение движения шарики принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Так как масса шарики и жесткость пружины для данной колебательной системы постоянны, отношение k m . . — постоянная величина. Отсюда делаем вывод, что проекция a x ускорения тела прямо пропорциональна его координате x, взятой с противоположным знаком.

Пример №1. Груз массой 0,1 кг прикрепили к пружине школьного динамометра жесткостью 40 Н/м. В начальный момент времени пружина не деформирована. После того, как груз отпускают, возникают колебания. Чему равна максимальная скорость груза?

Максимальной скорости груз достигнет при максимальном его отклонении от положения равновесия — в нижней точке траектории. Учтем, что тело движется вниз под действием силы тяжести. Но в то же время на него действует сила упругости, которая возникает в пружине и нарастает до тех пор, пока не становится равной по модулю силе тяжести. Применив III закон Ньютона получим:

∣ ∣ ∣ → F т я ж ∣ ∣ ∣ = ∣ ∣ ∣ → F у п р ∣ ∣ ∣

где y m a x — максимальное отклонение груза от положения равновесия. В этой точке скорость тела будет максимальная. Для нахождения этой величины используем формулу из кинематики:

y m a x = v 2 m a x − v 2 0 2 g . .

Начальная скорость равна нулю. Отсюда:

y m a x = v 2 m a x 2 g . .

m g = k v 2 m a x 2 g . .

Максимальная скорость равна:

v m a x = g √ 2 m k . . = 10 √ 2 · 0 , 1 40 . . ≈ 0 , 71 ( м с . . )

Уравнение движения математического маятника

Ниже на рисунке представлен математический маятник. Если мы выведем из положения равновесия шарик и отпустим, возникнет две силы:

сила тяжести, направленная вниз;
сила упругости, направленная вдоль нити.

При колебаниях шарика также будет возникать сила сопротивления воздуха. Но так как она очень мала, мы будем ею пренебрегать.

Чтобы описать динамику движения математического маятника, удобно силу тяжести разложить на две составляющие:

→ F т = → F τ + → F n

Причем компонента → F τ направлена перпендикулярно нити, а → F n — вдоль нее.

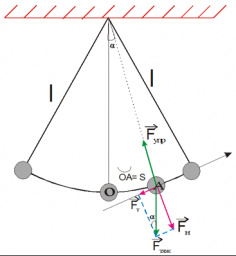
Компонента → F τ представляет собой проекцию силы тяжести в момент, когда нить маятника отклонена от положения равновесия (точки О) на угол α. Следовательно, она равна:

→ F τ = − → F т sin . α = − m g sin . α

Знак «–» мы здесь поставили по той причине, что компоненты силы тяжести → F τ и α имеют противоположные знаки. Ведь если отклонить шарик на угол α>0, то составляющая → F τ будет направлена в противоположную сторону, так как она будет пытаться вернуть шарик в положение равновесия. И ее проекция будет отрицательной. Если же шарик отклонить на угол α → F τ будет направлена в обратную сторону. В этом случае ее проекция будет положительной.

Обозначим проекцию ускорения маятника на касательную к его траектории через a τ . Эта проекция характеризует быстроту изменения модуля скорости маятника. Согласно II закону Ньютона:

m a τ = − m g sin . α

Разделим обе части выражения на массу шарика m и получим:

При малом отклонении нити маятника от вертикали можно считать, что sin . α ≈ α (при условии, что угол измерен в радианах). Тогда:

Внимание! Чтобы перевести градусы в радианы, нужно умножить градусы на число π и поделить результат на 180. К примеру 2 о = 2∙3,14/180 рад., или 2 о = 0,035 рад.

При малом отклонении также дугу ОА мы можем принять за длину отрезка OA, который мы примем за s. Тогда угол α будет равен отношению противолежащего катета (отрезка s) к гипотенузе (длине нити l):

Так как ускорение свободного падения и длина нити для данной колебательной системы постоянны, то отношение g l . . — тоже постоянная величина.

Это уравнение похоже на то уравнение, которое мы получили для описания колебательного движения шарика под действием силы упругости. И оно также позволяет сделать вывод, что ускорение прямо пропорционально координате.

Пример №2. Определить длину нити, если шарик, подвешенный к ней, отклонится на 1 см. При этом нить образовала с вертикалью угол, равный 1,5 о .

При отклонениях на малый угол мы можем пользоваться следующей формулой:

Чтобы найти длину нити, нужно выразить угол α в радианах:

1 , 5 ° = 3 , 14 · 1 , 5 180 . . ≈ 0 , 026 ( р а д )

Тогда длина нити равна:

l = s α . . = 0 , 01 0 , 026 . . ≈ 0 , 385 ( м ) = 38 , 5 ( с м )

Основные характеристики колебательного движения

Амплитуда — максимальное отклонение тела от положения равновесия. Обозначается буквой A, иногда — x_max. Единиц измерения — метр (м).

Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с).

Частота — количество колебаний, совершенных в единицу времени. Обозначается как ν («ню»). Единица измерения — 1/секунда, или секунда –1 , или герц (1/с, или с –1 , или Гц).

Период и частота колебаний связаны между собой следующей формулой:

Период колебаний также можно вычислить, зная количество совершенных колебаний N за время t:

Поскольку частота — это величина, обратная периоду колебаний, ее можно выразить в виде:

Пример №3. Определить частоту колебаний груза, если суммарный путь, который он прошел за 2 секунды под действием силы упругости, составил 1 м. Амплитуда колебаний равна 10 см.

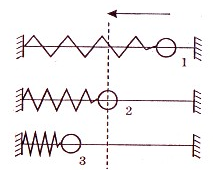
Во время одного колебания груз проходит расстояние, равное 4 амплитудам. Посмотрите на рисунок. Положение равновесия соответствует состояние 2. Чтобы совершить одно полное колебание, сначала груз отводят в положение 1. Когда его отпускают, он проходит путь 1–2 и достигает положения равновесия. Этот путь равен амплитуде колебаний. Затем он продолжает движение до состояния 3. И в это время он проходит расстояние 2–3, равное еще одной амплитуде колебаний. Чтобы вернуться в исходное положение (состояние 1), нужно снова проделать путь в обратном направлении: сначала 3–2, затем 2–1.

Следовательно, количество колебаний равно отношению пройденного пути к амплитуде, помноженной на 4:

Так как мы знаем, что эти колебания совершались в течение 2 секунд, для вычисления частоты мы можем использовать формулу:

ν = N t . . = s 4 A t . . = 1 4 · 0 , 1 · 2 . . = 1 , 25 ( Г ц )

В таблице представлены данные о положении шарика, колеблющегося вдоль оси Ох, в различные моменты времени.

Каков период колебаний шарика?

Алгоритм решения

Решение

Из таблицы видно, что амплитуда колебаний равна 15 мм. Следовательно, максимальное отклонение в противоположную сторону составляет –15 мм. Расстояние между двумя максимальными отклонениями от положения равновесия шарика равно половине периода колебаний. Этим значения в таблице соответствует время 1 и 3 секунды соответственно. Следовательно, разница между ними — половина периода. Тогда период будет равен удвоенной разнице во времени:

T = 2 ( t 2 − t 1 ) = 2 ( 3 − 1 ) = 4 ( с )

pазбирался: Алиса Никитина | обсудить разбор | оценить

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остается растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия?

Для каждой величины определите соответствующий характер изменения:

1)	увеличивается
2)	уменьшается
3)	не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Потенциальная энергия пружины определяется формулой:

где k — коэффициент жесткости пружины, а x — ее удлинение. Величина x была максимальной в нижней точке траектории. Когда пружина начинает сжиматься, она уменьшается. Так как потенциальная энергия зависит от квадрата x прямо пропорционально, то при уменьшении этой величины потенциальная энергия пружины тоже уменьшается.

Кинетическая энергия тела определяется формулой:

В нижней точке траектории скорость шарика была равна нулю. Но к этому времени потенциальная энергия пружины достигла максимума. Она начинает с ускорением поднимать шарик вверх, сжимаясь. Следовательно, скорость растет. Так как кинетическая энергия зависит от квадрата скорости тела прямо пропорционально, то при увеличении скорости этой величины кинетическая энергия шарика тоже увеличивается.

Потенциальная энергия тел в поле тяжести земли определяется формулой:

Масса и ускорение свободного падения шарика — постоянные величины. Следовательно, потенциальная энергия зависит только от расстояния до поверхности земли. Когда пружина поднимает шарик, расстояние между ним и землей увеличивается. Так как потенциальная энергия зависит от расстояния прямо пропорционально, то при его увеличении потенциальная энергия шарика тоже растет.

pазбирался: Алиса Никитина | обсудить разбор | оценить

В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.

Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.

А) Потенциальная энергия пружины в момент времени 1,0 с максимальна.

Б) Период колебаний шарика равен 4,0 с.

В) Кинетическая энергия шарика в момент времени 2,0 с минимальна.

Г) Амплитуда колебаний шарика равна 30 мм.

Д) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.

Алгоритм решения

Проверить истинность каждого утверждения.
Выбрать 2 верных утверждения.

Решение

Согласно утверждению «А», потенциальная энергия пружины в момент времени 1,0 с максимальна. Потенциальная энергия пружины максимальна, когда она отклоняется от положения равновесия на максимальную возможную величину. Из таблицы видно, что в данный момент времени ее отклонение составило 15 мм, что соответствует амплитуде колебаний (наибольшему отклонению от положения равновесия). Следовательно, утверждение «А» — верно.

Согласно утверждению «Б», период колебаний шарика равен 4,0 с. Один период колебаний включает в себя 4 фазы. В течение каждой фазы шарик на пружине проделывает путь, равный амплитуде. Следовательно, мы можем найти период колебаний, умножив время одной фазы на 4. В момент времени t = 0 с, шарик находился в положении равновесия. Первый раз он отклонился на максимальную величину (15 мм) в момент времени t = 1,0 с. Значит, период колебаний равен 1∙4 = 4 с. Следовательно, утверждение «Б» — верно.

Согласно утверждению «В», кинетическая энергия шарика в момент времени 2,0 с минимальна. В этот момент времени, согласно данным таблицы, шарик проходит положение равновесия. В этом положении скорость шарика всегда максимальна. Поэтому кинетическая энергия, которая зависит от квадрата скорости прямо пропорционально, минимальной быть не может. Следовательно, утверждение «В» — неверно.

Согласно утверждению «Г», амплитуда колебаний шарика равна 30 мм. Амплитуда колебаний — есть расстояние от положения равновесия до точки максимального отклонения шарика. В данном случае оно равно 15 мм. Следовательно, утверждение «Г» — неверно.

Согласно утверждению «Д», полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна. Полная механическая энергия колебательной системы — это совокупность кинетической и потенциальной энергий. И при отсутствии сил трения она остается величиной постоянной. Она лишь превращается из одного вида энергии в другую. Следовательно, утверждение «Д» — неверно.

pазбирался: Алиса Никитина | обсудить разбор | оценить

источники:

http://natalibrilenova.ru/garmonicheskoe-kolebanie-uravnenie-avtokolebaniya-mehanicheskij-rezonans/

http://spadilo.ru/mexanicheskie-kolebaniya/