Уравнения гельмгольца в комплексной форме

Тема 5. волновые уравнения для векторов ЭМП

Однородные и неоднородные волновые уравнения для векторов ЭМП. Уравнения Даламбера. Решение однородных уравнений Даламбера. Сферическая волна. Волновой фронт. Волновые уравнения Гельмгольца.

Плоские волны как частные решения волновых уравнений. Плоская волна как предельный случай сферической волны. Решения волновых уравнений для гармонических полей в виде плоских и сферических волн.

Плоские ЭМВ в однородной изотропной среде. Отличие понятий «волна» и «колебание». Свойства плоской волны, структура и ориентация векторов ЭМП. Коэффициенты фазы и ослабления. Длина волны. Фазовая скорость, скорость распространения энергии, групповая скорость.

Характеристическое и волновое сопротивления. Ослабление ЭМВ, глубина проникновения ЭМП в вещество.

Указания к теме

Решением волновых уравнений являются функции координат и времени, которые описывают ЭМВ, распространяющиеся в свободном пространстве, направляющих системах и других устройствах. Необходимо получить четкое представление о таких понятиях, как фазовая поверхность (волновой фронт) и ее форма, однородная и неоднородная волна, затухающая волна.

Следует выучить определения длины волны, коэффициентов затухания и фазы, групповой и фазовой скоростей, волнового и характеристического сопротивлений, глубины проникновения ЭМВ в вещество.

Основные сведения

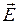
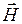
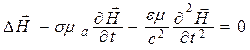
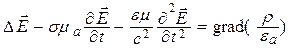
Для анализа распространяющихся ЭМВ из системы уравнений Максвелла в дифференциальной форме целесообразно вывести уравнения, которые зависят либо только от , либо только от . Если параметры среды (s, e, m) не зависят от координат и времени, то после преобразований получим [1–6]

; (5.1)

. (5.2)

Как показали расчеты и эксперименты, константа с ( 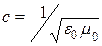) для ЭМП удивительным образом совпадает со значением скорости света в вакууме. Из этого был сделан вывод о том, что ЭМВ и свет имеют одну и ту же природу. В пространстве без потерь ЭМВ распространяются со скоростью света.

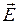
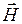
Уравнения (5.1) и (5.2) называют волновыми уравнениями Ж. Д’Аламбера [5, 12]. Если правая часть равна нулю, то уравнение называют однородным, а если нет – неоднородным. При отсутствии электрических зарядов (r = 0) уравнения (5.1) и (5.2) практически совпадают, что подтверждает равноправие векторов и у распространяющегося в пространстве ЭМП.

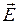
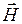
Несмотря на кажущуюся независимость уравнений (5.1) и (5.2), следует помнить о том, что у переменного ЭМП векторы и связаны уравнениями Максвелла и не могут существовать друг без друга.

Волновые уравнения в комплексной форме имеют вид

; , (5.3)

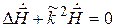
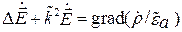
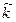
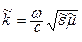
где – волновое число:

. (5.4)

Уравнения (5.3) называют волновыми уравнениями Г. Гельмгольца. При отсутствии потерь проводимости (s = 0) исчезают вторые слагаемые в уравнениях (5.1) и (5.2), а также в (5.3)–(5.4) возможно упрощение:

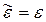
Рассмотренные уравнения называются волновыми потому, что их решениями являются волны и, в частности, ЭМВ.

Фазовым фронтом волны называют поверхность, проходящую через точки с одинаковыми фазами, по форме этой поверхности определяется название волны (сфера – сферическая ЭМВ, плоскость – плоская и т. д.) [1–3].

Решение однородного волнового уравнения для плоских волн

. (5.5)

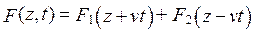
Каждое из слагаемых выражения (5.5) описывает возмущения F₁ и F₂, исходящие из точки z₀ в момент t = 0 и к моменту времени t приходящие в точку z = z₀ – vt для F₁ и в точку z = z₀ + vt для F₂ со скоростью v [1].

Для сферических волн решение волнового уравнения имеет вид:

. (5.6)

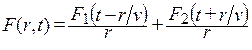
Первое слагаемое выражения (5.6) представляет собой сферическую волну, расходящуюся от источника. Второе слагаемое часто отбрасывают, поскольку волна, движущаяся внутрь источника, обычно не рассматривается [1].

В отличие от выражения (5.5) амплитуда сферической волны (5.6) уменьшается при удалении от источника как 1/r (мощность – как 1/r 2 ), что связано с тем, что мощность изотропного источника распределяется по расходящимся сферам (4.10).

Таким образом, даже при отсутствии потерь в пространстве плотность потока мощности сферической волны уменьшается с расстоянием как 1/r 2 .

На большом расстоянии от источника ЭМВ (в дальней зоне антенны) сферический волновой фронт в области приемной антенны можно аппроксимировать плоскостью, подобно тому, как земную поверхность считают плоской при малых высотах и на дистанциях, много меньших расстояния прямой видимости.

Плоская ЭМВ – идеализированная волна, имеющая плоский фазовый фронт (z = const), у которой существуют две взаимно перпендикулярные составляющие и , зависящие только от координаты z и расположенные в плоскости, перпендикулярной z. ЭМВ называется однородной, если ее амплитуда постоянна во всех точках фазового фронта, и неоднородной, если ее амплитуда зависит от координат точек фазового фронта.

В дальнейшем будем считать, что направление распространения ЭМВ совпадает с осью z. Уравнения Максвелла в комплексной форме для составляющих векторов плоской волны в ДСК имеют вид

; ; ; . (5.7)

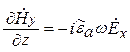
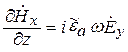
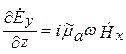
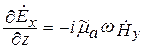
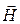
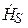
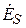
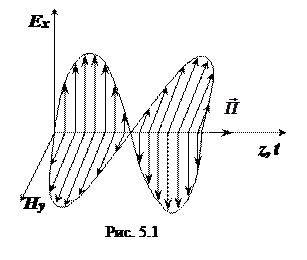
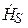
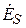
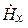
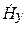
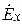
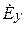
Из формул (5.7) следует, что и взаимно перпендикулярны. (Это можно доказать, рассмотрев скалярное произведение векторов [11].) В дальнейшем будем обозначать координаты этих векторов и , подчеркивая их поперечную направленность и расположение в плоскости x0y.

Зная или , можно легко найти другую поперечную составляющую и перейти к обычным координатам ( , , , ).

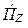
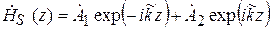
Вектор Пойнтинга в данном случае имеет только продольную составляющую (рис. 5.1). Решение уравнений (5.3) имеет вид

. (5.8)

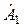
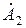
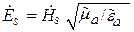
Первое слагаемое выражения (5.8) соответствует прямой волне, второе слагаемое – обратная волна, и – комплексные амплитуды данных бегущих волн (для – аналогично). Подставляя выражение (5.8) в (5.7), получим

. (5.9)

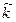
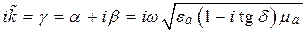
Запишем связь волнового числа ( ) с комплексным коэффициентом распространения (g) для среды без магнитных потерь :

, (5.10)

Уравнение плоской волны с учетом (5.10) можно записать в виде

. (5.11)

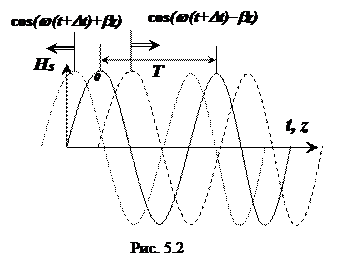
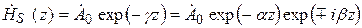
Для мгновенных значений из выражения (5.11) получаем

. (5.12)

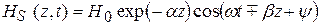
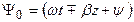
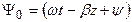
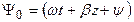
Направление распространения ЭМВ можно определить из анализа зависимости полной фазы (5.12) от времени. Зафиксировав волновой фронт в какой-то момент времени, получаем, что если , то в следующий момент времени ЭМВ сместится в положительном направлении оси z, а при волновой фронт будет двигаться в отрицательном направлении оси z(рис. 5.2) [1].

Из анализа формул (5.10)–(5.12) очевидно, что a– это коэффициент затухания, а b – коэффициент фазы.

Подставляя формулу (5.12) в (5.1), после решения уравнений относительно a и b получаем

, (5.13)

. (5.14)

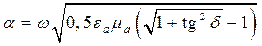
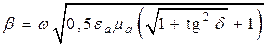
Множитель 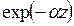в выражениях (5.10)–(5.12) показывает затухание при распространении ЭМВ вдоль оси z. Чем больше a, тем больше затухание.

Ослаблением (A) ЭМВ по полю называют величину (A_P = A 2 – ослабление ЭМВ по мощности)

, . (5.15)

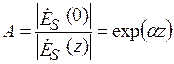
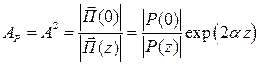
На практике часто используют ослабление в децибелах (дБ):

. (5.16)

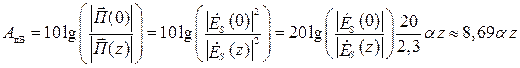
С ослаблением непосредственно связана глубина проникновения ЭМП в вещество (D° ), называемая также толщиной поверхностного слоя (скин-слоя, но это понятие логичнее использовать для металлов):

. (5.17)

При прохождении слоя вещества z =D° амплитуда ЭМП ослабляется в е (е = 2,718…) раз, и соответственно в следующий слой (рис. 5.3) проходит лишь 1/е 2 мощности ЭМП. Получается, что в поверхностном слое D° концентрируется 86,5% энергии ЭМП, в слое 2D° – 98,2%,а в слое 3D° – 99,8%.

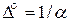
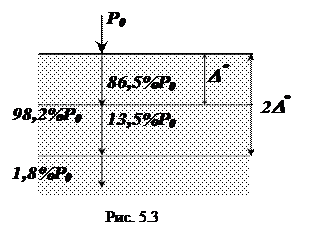
Таким образом, зная коэффициент затухания, можно определить область преимущественной концентрации энергии ЭМВ в веществе.

В случае диэлектриков толщина поверхностного слоя значительна, в то время как для проводников на ВЧ и ОВЧ она составляет доли миллиметра [1].

Параметры ЭМВ. Длиной волны l называется расстояние между двумя фронтами ЭМВ, различающимися по фазе на 2p (360°):

. (5.18)

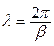
Фазовой скоростью v_ф называется скорость перемещения фазового (волнового) фронта ЭМВ. При анализе выражения (5.12) ранее были определены направление движения и скорость фронта ЭМВ

. (5.19)

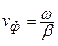
Фазовая скорость может изменяться в любых пределах (может быть больше с!), поскольку не является скоростью переноса энергии [1].

Групповой скоростью v_гр называют скорость движения фронта (например, максимума) огибающеймодулированного сигнала.

Информационный сигнал не является монохроматическим, он занимает полосу частот. Каждая спектральная составляющая может иметь свою скорость распространения, что в диспергирующих средах приводит к искажениям сигнала.

Понятие «групповая скорость» вводится для сред с малыми потерями, поэтому при Dw v_ф ( 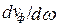>0).

При Dw/w₀ ® 0 период огибающей стремится в бесконечность, понятие «группа волн» распространяется на весь сигнал, и в итогеv_гр ® v_Э.

Групповая скорость узкополосного сигнала – это скорость передачи энергии, она не может быть выше скорости света.

Характеристическое сопротивление (Z_с) [41] ЭМВ равно отношению амплитуд поперечных составляющих электрического и магнитного полей

. (5.21)

При комплексном Z_с отстает или опережает по фазе вектор на некоторый угол. На рис. 5.5 вектор опережает на 90° (π/4), а на рис. 5.1 данные векторы синфазны.

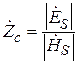
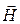
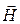
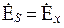
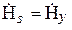
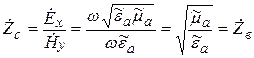
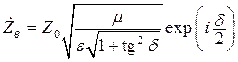
Определим характеристическое сопротивление плоской волны. Пусть , а , тогда из формул (5.7) следует:

, . (5.22)

Получается, что характеристическое сопротивление [41]зависит только от параметров среды. Z_в называют волновым сопротивлением среды. Следует отметить, что стандартом [41] рекомендуется термин «характеристическое сопротивление». Для ЭМВ, распространяющейся в некоторой среде, Z_c = Z_в.

Волновое сопротивление вакуума Z₀ (s = 0, e = m = 1) :

377,0 Ом. (5.23)

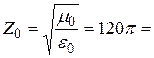
Тогда выражение (5.22) можно записать в виде

. (5.24)

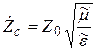
Список рекомендуемой литературы:[1, гл. 6–7, с. 30–38; 2, с. 50–56; 3, гл. 6–7, с. 27–34; 4, с. 26–33; 5, с. 26–30; 6, с. 116–123, 128–142, 198–205; 7, с. 67–82, 250–259; 8, с. 62–68; 9, с. 69–74; 10, с. 68–73; 11, с. 67–69, 130–139; 12, с. 182–194; 13, с. 140–149, 174–177, 187–190; 15, с. 302–307].

Контрольные вопросы и задания

1. Почему рассматриваемые в этой теме уравнения называются волновыми?

2. Чем волна отличается от колебания?

3. Чем отличаются волновые уравнения Д’Аламбера и Гельмгольца?

4. Следует ли из волновых уравнений независимость электрической и магнитной составляющих ЭМП?

5. Можно ли считать свет ЭМ волной?

6. Какие упрощения возможны в волновых уравнениях для сред без потерь?

7. Можно ли по виду электрической или магнитной составляющей плоской ЭМВ определить расположение другой составляющей ЭМП и направление распространения ЭМВ?

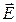
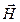
8. При каких условиях волновые уравнения для векторов и идентичны?

9. Каково простейшее решение системы уравнений Максвелла?

10. Дайте определение волнового фронта.

11. Почему плотность потока энергии сферической волны уменьшается при удалении от источника даже в пространстве без потерь?

12. Какие упрощения в анализе ЭМП дает понятие «плоская волна»? В каких практических случаях допустимо ЭМВ считать плоской?

13. Чем отличаются однородные и неоднородные плоские волны?

14. Дайте определение коэффициентам затухания и фазы плоской ЭМВ.

15. Чем отличается волновое число k от g ?

16. Какова пространственная структура плоской ЭМВ?

17. Как определить направление распространения ЭМВ?

18. Как с помощью понятия толщины поверхностного слоя можно оценить область преимущественной концентрации ЭМП?

19. Дайте определение основным характеристикам ЭМВ.

20. Чем групповая скорость отличается от фазовой?

21. Может ли фазовая скорость иметь бесконечное значение?

22. Чем волновое сопротивление отличается от характеристического?

23. Является ли групповая скорость скоростью передачи энергии?

24. Что такое дисперсия? Приведите примеры дисперсионных сред.

25. Укажите условие неискаженной передачи сигнала.

26. Чем нормальная дисперсия отличается от аномальной?

Уравнения гельмгольца в комплексной форме

Волновой оптикой называют раздел физической оптики, изучающей явления, в которых проявляется волновая природа света. В этом разделе в кратком изложении сформулированы основные теоретические положения волновой оптики и приведены наиболее важные соотношения и уравнения, положенные в основу всего дальнейшего рассмотрения. 1.2.1. Волновое уравнение По своей физической природе световые волны являются волнами электромагнитными. Поэтому волновая оптика непосредственно основывается на уравнениях Максвелла.

Уравнения Максвелла связывают вектор напряженности электрического поля E и вектор электрической индукции D с вектором напряженности магнитного поля H и вектором индукции B . В отсутствие токов и свободных электрических зарядов они имеют вид:

где и — соответственно электрическая и магнитная постоянные, и — относительные соответственно диэлектрическая и магнитная проницаемости среды.

Подставим величину (1.2.6) в уравнение (1.2.2) и, предполагая, что величина не зависит от пространственных координат, возьмем ротор от левой и правой частей этого уравнения

Используя уравнения (1.2.1) и (1.2.5), а также принимая во внимание, что

можно переписать уравнение (1.2.7) в виде

Присутствующий в соотношениях (1.2.8), (1.2.9) оператор является вектором с компонентами . Если величина постоянна в пространстве, градиент обращается в нуль, и уравнение (1.2.9) принимает вид волнового уравнения

Применяя операцию к обеим частям уравнения (1.2.1), можно получить аналогичное уравнение для

Из (1.2.11) следует, что каждая декартова компонента Y w (x,y,z,t) вектора или B удовлетворяют скалярному волновому уравнению

где величина v имеет физический смысл скорости света в среде с параметрами e и m

Частным решением уравнения (1.2.12) может служить плоская волна произвольной формы, распространяющаяся в направлении n . Если в каждой точке пространства величина меняется во времени по гармоническому закону, то плоская волна может быть описана выражением

где w — циклическая частота, а — амплитуда.

Вводя волновой вектор , модуль которого равен k =2 p / l , выражению (1.2.14) можно придать вид

В расчетах удобно пользоваться комплексным представлением плоской гармонической волны

В комплексной форме могут быть представлены также расходящиеся и сходящиеся сферические волны, которые имеют соответственно вид

Поскольку нас интересует преимущественно монохроматическое излучение, то есть излучение определенной частоты, мы будем в дальнейшем опускать экспоненциальный множитель

Если зависимость от времени представляется в форме (1.2.19), то дифференцирование по времени заменяется умножением на -i w и волновое уравнение (1.2.12) принимает вид

где под Y следует понимать комплексную амплитуду волны. Уравнение (1.2.20) называется приведенным волновым уравнением Гельмгольца. В нашем курсе это уравнение играет фундаментальную роль. В последующих разделах нам придется неоднократно к нему обращаться в процессе анализа особенностей распространения волновых пучков в различных средах и оптических системах.

До сих пор обсуждение касалось волнового уравнения (1.2.12), полученного как частный случай уравнения (1.2.9). Поскольку первое из них является существенно более простым и удобным, возникает вопрос о возможности его применения также для случая неоднородных сред. Для ответа на этот вопрос следует определить, в каких случаях можно пренебречь вторым членом в уравнении (1.2.9). Доминирующими членами в уравнении (1.2.9) являются первый член в левой части и член в правой части, порядок величин которых одинаковый. Возьмем отношение второго члена левой части уравнения (1.2.9) к члену, стоящему в правой части

Несложный анализ, выполненный в [8], показывает, что порядок R определяется соотношением

где , — значения относительной диэлектрической проницаемости в двух близких точках, разделенных расстоянием , e — ее среднее значение. Выбирая = l , получаем

Для того чтобы пренебречь вторым членом в левой части уравнения (1.2.9), необходимо потребовать выполнения условия R e на расстоянии длины волны должно быть много меньше 1. Для большинства неоднородных оптических сред такое условие хорошо выполняется, что позволяет ограничиваться решением уравнения (1.2.10) вместо (1.2.9). Только на границе раздела двух областей с различными диэлектрическими проницаемостями, например, на границе между стеклянными линзами и воздухом, величина R становится большой. Однако даже в этих случаях следует решать уравнение (1.2.10) или (1.2.12), так как оно справедливо всюду, кроме границы раздела сред. На практике обычно решают волновое уравнение в различных однородных областях и сшивают эти решения посредством граничных условий.

1.2.2. Теория дифракции по Кирхгофу В основе волновых представлений о распространении когерентого излучения лежит теория дифракции. Под дифракцией света обычно понимают отклонения от простых законов распространения света, описываемых геометрической оптикой. Дифракцию можно наблюдать, когда на пути распространения света находятся непрозрачные препятствия или когда свет проходит через отверстия в экранах. С дифракцией непосредственно связан физический механизм, обуславливающий перераспределение интенсивности в поперечном сечении пространственно-неоднородных лазерных пучков при их распространении в свободном пространстве. В большинстве случаев при описании дифракции можно не учитывать поляризации световой волны. Поэтому в основу теории дифракции мы положим скалярное уравнение Гельмгольца (1.2.20).

Пусть в пространстве распространяется монохроматическая волна

амплитуда которой Y ( x,y,z ) удовлетворяет уравнению Гельмгольца (1.2.20). Окружим точку наблюдения Р произвольной поверхностью S ( рис . 1.2.1.).

Определим возмущение в точке Р в зависимости от возмущения на границе выделенной области. Воспользуемся для этого известной теоремой Грина

где c — некоторая вспомогательная величина, которая также как и Y имеет непрерывные частные производные первого и второго порядков внутри объема V , ограниченного поверхностью S , и на самой поверхности S . Потребуем также, чтобы функция c удовлетворяла уравнению (1.2.20). Операция в формуле (1.2.25) означает дифференцирование по внутренней нормали к поверхности S . В качестве вспомогательной функции c рассмотрим функцию , где r — расстояние между произвольной точкой объема V и точкой Р (радиус-вектор r будем считать направленным от точки Р , как от начала координат). Функция c представляет собой функцию изменения амплитуды поля точечного источника (т.е. так называемую функцию Грина свободного пространства). Для того чтобы эта функция удовлетворяла условиям теоремы Грина, нужно исключить из области V точку Р , где функция c обращается в бесконечность. С этой целью окружим точку Р сферой бесконечно малого радиуса R и исключим ее из области V . Тогда формула (1.2.25) примет вид

Здесь означает объем V без объема сферы, — площадь сферы. Поскольку функции Y и c удовлетворяют уравнению Гельмгольца, то объемный интеграл в выражении (1.2.26) равен нулю. Тогда из (1.2.26) следует, что

При выводе соотношения (1.2.27) мы перешли от интегрирования по поверхности к интегрированию по телесному углу W . Таким образом, возмущение в точке Р будет равно

Выражение (1.2.28) известно как дифракционный интеграл Кирхгофа-Гюйгенса.

Дифракционный интеграл (1.2.28) широко используется при решении многих дифракционных задач. Следует, однако, иметь в виду, что возможны и другие математические подходы к анализу дифракции. Они, прежде всего, связаны с выбором другой вспомогательной функции c . В частности, функция c может быть выбрана так, чтобы она обращалась в ноль на поверхности S . Такой подход в какой-то степени упрощает задачу, так как в выражении (1.2.28) обращается в ноль член, содержащий . Однако цена этого упрощения состоит в усложнении функции c .

Для большинства оптических задач выполняется условие

тогда, пренебрегая производной от по сравнению с производной от , формулу (1.2.28) можно записать в виде

Рассмотрим классическую для теории дифракции задачу о прохождении плоской волны через отверстие площадью А в бесконечном непрозрачном экране ( рис. 1.2.2). Будем считать, что поверхность, по которой происходит интегрирование, включает экран и бесконечную

полусферу радиуса , ограничивающую пространство справа от экрана. Обозначим координаты точки Р как , , , угол наклона волнового вектора k плоской волны и оси z через g , а угол, задающий направление на точку Р , через a . Из рис . 1.2.2 следует, что

С помощью формул (1.2.32) и (1.2.33) интеграл (1.2.30) можно переписать в виде

В таком виде этот интеграл известен как формула (интеграл) Френеля-Кирхгофа. В выражении (1.2.34) мы ограничились интегрированием лишь по площади отверстия, считая, что интеграл по бесконечной полусфере обращается в ноль. Последнее утверждение выглядит вполне обоснованным, если предположить, что падающая волна представляет собой очень длинный, но все же конченый цуг волн. Конечный же цуг волн не может достичь бесконечной полусферы за конечное время, тем самым интеграл по поверхности этой полусферы равен нулю.

Более точный математический анализ показывает, что интеграл по бесконечной полусфере стремится к нулю, если выполняется так называемое условие Зоммерфельда, согласно которому

Гораздо боле уязвимым предположением является использованное при получении формулы (1.2.34) второе предположение о равенстве нулю функции Y и ее производной на непрозрачном экране. Дело в том, что равенство нулю решения волнового уравнения и его производной на любом конечном интервале приводит к обращению его в ноль во всем объеме. Однако, несмотря на явный математический изъян, формула (1.2.34) приводит к результатам, хорошо согласующимся с данными экспериментов.

Во многих практических случаях, когда отверстие в экране мало и точка Р располагается вблизи оси, можно считать, что

Одновременно, если экран освещается волной, падающей на него перпендикулярно, можно положить, что

Тогда формула (1.2.34) преобразуется в выражение

которое является математическим обобщением принципа Гюйгенса-Френеля. Из него видно, что недостаточно просто предполагать, как это делал в свое время Гюйгенс, что падающая волна выполняет роль источника сферических волн с амплитудами, пропорциональными амплитуде падающей волны в каждой точке. Необходимо потребовать, чтобы фаза вторичного источника отставала от фазы падающей волны на (из-за наличия в правой части (1.2.37) множителя -i).

Поскольку в большинстве практических случаев выполняются соотношения

можно построить выражение для величины r , ограничиваясь первыми двумя членами ее разложения в ряд Тейлора

Используя это выражение, получим следующее приближение для формулы Френеля-Кирхгофа (1.2.34):

Принято говорить о двух случаях применения интеграла (1.2.40): дифракции Френеля и дифракции Фраунгофера. Дифракция Френеля имеет место, когда поле рассчитывается на небольшом расстоянии от отверстия и член , появляющийся в показателе степени экспоненты, следует принимать во внимание. Дифракция же Фраунгофера наблюдается вдали от отверстия, когда этот член пренебрежительно мал.

Вторичные сферические волны, излучаемые каждой точкой в плоскости отверстия, являются в определенном смысле абстракцией и вводятся в приведенном выше подходе к решению дифракционных задач, главным образом, для удобства описания. Более физический подход развит в работах Зоммерфельда. Зоммерфельд рассматривал высказанную еще в 1802 г. Томасом Юнгом идею, заключающуюся в следующем: наблюдаемое поле является суперпозицией падающей волны, прошедшей через отверстие без искажения, и дифрагированной волны, источником которой служит край отверстия. Однако на этом подходе мы подробно останавливаться не будем.

1.2.3. Дифракция Френеля Анализ дифракции Френеля в общем случае или применительно к прохождению света через сколь-нибудь сложные неоднородные структуры представляет собой непростую задачу. Поэтому мы ограничимся рассмотрением дифракции Френеля на квадратном отверстии со стороной l . Представим выражение (1.2.40) в виде произведения двух интегралов, считая углы g и a пренебрежимо малыми:

Интегралы существенно упрощаются после замены переменных

и переходят в следующие интегралы

где пределы интегрирования определяются соотношениями

Интегралы Ф(x’) и Ф(y’) можно выразить через табулированные функции, известные под названием интегралов Френеля. Последние определяются выражениями

Наконец, подставляя (1.2.45) в (1.2.41), получаем распределение комплексного поля

и соответствующее распределение интенсивности

Для интерпретации этих выражений удобно воспользоваться графическим построением, которое называется спиралью Корню; спираль Корню ( рис. 1.2.3) представляет собой совместный график зависимости C( a ) и S ( a ) от параметра a .

Заметим, что величину C( a )+iS( a ) можно считать комплексным фазором, соединяющим начало координат с точкой a на спирали. Следовательно, величина представляет собой фазор, определяемый участком спирали между точками x 1 и x 2. Используя подобный графический метод, можно вычислить значение выражений (1.2.46) и (1.2.47) в каждой точке дифракционной картины.

1.2.4. Дифракция Фраунгофера. Элементы фурье-оптики Скалярную теорию дифракции можно облечь в иную форму, если применить двумерный анализ Фурье. В дальнейшем мы воспользуемся тем, что при фурье-анализе распределения светового поля в любой плоскости пространственные составляющие его фурье-образа можно отождествить с плоскими волнами, идущими в разных направлениях. Складывая амплитуды этих волн и учитывая их фазовые набеги, можно вычислить амплитуду поля в любой интересующей нас точке пространства. Раздел физической оптики, в котором для описания преобразований структуры светового поля используется двумерный анализ Фурье, называется фурье-оптикой. Особенно удобно использовать аппарат фурье-оптики для характеристики дифракции Фраунгофера.

Пусть в некоторой плоскости < x,y,0 >задана комплексная амплитуда световой волны, распространяющейся в положительном направлении оси z. Рассмотрим трансформацию поля волны при ее распространении. Выясним сначала, какой физический смысл имеет фурье-образ функции .

В плоскости < x,y ,0>двумерный фурье-образ функции Y имеет вид

С помощью фурье-образа функцию y можно представить в виде совокупности простых экспоненциальных функций

Из формулы (1.2.16) следует, что для комплексной амплитуды плоской волны справедливо выражение

где a , b , g — направляющие косинусы нормали к фронту плоской волны, причем . Тем самым комплексную экспоненциальную функцию , входящую в выражение (1.2.42), можно рассматривать как плоскую волну с направляющими косинусами

и комплексной амплитудой, равной , где , . Таким образом, можно считать, что выражение (1.2.42) задает угловой спектр возмущения в плоскость, параллельную первоначальной, но смещенную от нее на расстояние z, ее угловые составляющие сохранят свои амплитуды. Все изменения сведутся лишь к изменению фаз угловых составляющих спектра, поскольку плоские волны, распространяясь под разными углами, проходят разные расстояния. Иная ситуация будет иметь место, если на пути распространения волны будут находиться какие-либо препятствия.

Предположим, что на пути распространения волны с угловым спектром находится экран с амплитудным коэффициентом пропускания t(x,y). В плоскости непосредственно за экраном распределение поля можно записать в виде

где — поле падающей волны. По теореме свертки — важнейшей теореме анализа Фурье, — для углового спектра пропущенной экраном волны будет справедливо выражение

где Т — фурье-образ функции t(x,y).

Если на экран перпендикулярно падает плоская волна единичной амплитуды, то ее угловой спектр будет определяться d -функцией

В этом случае (1.2.46) упрощается

Таким образом, для рассмотренного частного случая угловой спектр дифрагированной волны представляет собой фурье-образ функции пропускания t(x,y). Как правило, помещение на пути распространения волны какой-либо ограничивающей апертуры приводит к существенному уширению углового спектра, причем это уширение тем больше, чем меньше размер апертуры.

Применим теперь анализ Фурье для описания дифракции Фраунгофера на отверстии. Разложим квадратичные члены в экспоненте, стоящей под интегралом в выражении (1.2.40), ограничиваясь случаем, когда :

Учтем также, что при дифракции Фраунгофера

Тогда можно считать, что квадратичная фазовая функция приблизительно равна единице по всему отверстию, и в точке с координатами поле равно

Поскольку последний интеграл представляет собой фактически фурье-образ функции с пространственными частотами , то обозначая фурье-образ как , имеем

Отсюда видно, что расчет распределения поля дифрагированной волны фактически сводится к нахождению фурье-образа поля сразу за экраном. Если экран освещается плоской когерентной волной с единичной амплитудой, то . Ниже приводятся фурье-образы функций пропускания для наиболее важных в практическом отношении случаев.

1. Прямоугольное отверстие

— размеры отверстий соответственно в направлении х и у ,

2. Круглое отверстие

D -диаметр отверстия,

где — функция Бесселя первого порядка.

3. Синусоидальная амплитудная решетка

L — размер квадратной решетки, — ее частота, m — разность между максимальным и минимальным пропусканием.

4. Дифракционная решетка — непрозрачный экран размером L , имеющий N щелей шириной а (щели располагаются строго периодически в направлении у , на расстоянии b одна за другой, так что период решетки составляет d=a+b )

5. «Мягкая» диафрагма с гауссовым профилем пропускания

На последнем примере следует остановиться особо. Из формул (1.2.60) и (1.2.61) следует, что, если световая волна имеет в поперечном сечении гауссово распределение амплитуды (такую волну можно получить, например, пропуская плоскую однородную волну через диафрагму с профилем (1.2.60), то ее фурье-образ также будет характеризоваться функцией Гаусса. Благодаря этому обстоятельству, «гауссовый» световой пучок, распространяясь в свободном пространстве, будет сохранять неизменной форму распределения амплитуды поля. Более подробно свойства гауссова пучка будут рассмотрены в следующей главе. 1.2.5. Принцип Бабине. Эффект Талбота Рассмотрим в силу практической значимости более подробно два случая дифракции на плоских экранах. Пусть задан некоторый экран. Заменой отверстий на непроницаемые участки и наоборот можно получить так называемый дополнительный экран. Если Y 1 и Y 2 — дифрагированные поля на этих двух экранах, то имеет место следующее соотношение (принцип Бабине)

где — поле в отсутствие экрана. Соотношение (1.2.62) непосредственно следует из (1.2.40), если интегрирование в этом соотношении выполнить по всей плоскости. Остается лишь предположить, что поля и на отверстиях первого и второго экрана совпадают с полем , которое имеет место в отсутствие экрана. Вообще говоря, принцип Бабине выполняется лишь приближенно, так как и не равны , но нарушение (1.2.62) существенно лишь вблизи границ диафрагм.

Второй случай относится к дифракционным полям, имеющим вид периодических функций. Он имеет интересные приложения для теории решеток и теории модульных лазерных систем.

Пусть цилиндрическое поле , фаза которого не зависит от координаты y, в плоскости z=0 записывается в виде

где — периодическая функция координаты x , содержащая столько гармоник N , что . Тогда для ближней зоны дифракции можно использовать дифракционную формулу Френеля (1.2.40), и мы имеем

Следует заметить, что в частном случае ( q =1, 2, . ) имеет место соотношение , так что

Отсюда следует, что во всех плоскостях zq распределение интенсивности поля одинаково. Это свойство называют эффектом Талбота, или эффектом самовоспроизведения. Оно было впервые замечено Талботом в 1836 г. и имеет весьма важные применения в фурье-спектроскопии, интерферометрии и оптике лазеров.

1.2.6. О возможности обобщения метода Кирхгофа на случай векторных полей Математическая не строгость теории дифракции приводит к тому, что она не может быть использована для расчета характеристик поля в непосредственной близости от отверстий в непрозрачных экранах. Кроме того, приемлемая точность расчетов может быть обеспечена лишь в тех случаях, когда размеры отверстий немного превосходят длину волны. Указанные ограничения сужают диапазон возможных приложений скалярной теории. Например, она не может быть использована для расчета характеристик дифракционных решеток высокого разрешения.

Применение скалярных методов для описания дифракции линейно поляризованной волны приводит к еще одному серьезному противоречию. оно состоит в том, что скалярные методы приводят к выводу о наличии продольных компонент поля за экраном (рис . 1.2.4.). Тем самым существует необходимость построения теории дифракции на основе более

последовательного векторного подхода.

Формальное обобщение метода Кирхгофа на случай векторных полей можно осуществить, записав для каждого компонента вектора интеграл Кирхгофа (1.2.25), а затем, сложив их векторно. В результате этой процедуры получается следующее выражение для :

Учитывая, что и , путем математических преобразований, получаем

где m — магнитная проницаемость среды.

Аналогичное выражение можно получить и для вектора .

Определяемый формулой (1.2.67) вектор не будет удовлетворять уравнениям Максвелла. Причина состоит в том, что тангенциальные компоненты векторов и терпят разрыв при переходе через границу контура отверстия. Для того, чтобы удовлетворить условиям непрерывности, необходимо ввести некоторое распределение зарядов и токов на контуре отверстия в экране.

Электродинамический анализ показывает, что самосогласованное поле дифрагированной волны с учетом дополнительных источников поля, обусловленных указанными зарядами, получается добавлением к поверхностному интегралу (1.2.67) интеграла по контуру отверстия

где t — единичный вектор, касательный к элементу контура отверстия dl . Обход контура диафрагмы осуществляется против часовой стрелки, если смотреть из точки, в которой определяется поле. С увеличением расстояния от точки наблюдения до отверстия вклад интеграла по контуру в величину поля снижается и на расстояниях многих длин волн им вообще можно пренебречь.

Электродинамические потенциалы гармонического поля

Раздел 5. Электродинамические потенциалы гармонического поля.

Практически все задачи электродинамики разделяют на 2 вида:

1. прямые задачи, в которых по заданному распределению сторонних источников необходимо определить соответствующее распределение электромагнитного поля.

2. обратные задачи, в которых по заданному распределению электромагнитного поля надо определить соответствующее распределение сторонних источников.

В этом разделе рассмотрим основные методы решения прямых задач электродинамики применительно для гармонического ЭМ поля и однородных линейных изотропных сред.

Относительно мгновенных значений векторов поля задачи решают очень редко, из-за сложности их определения. Обычно задачи решают для гармонических полей с использованием метода комплексных амплитуд. При решении любых электродинамических задач очень редко используют непосредственно уравнения Максвелла. Обычно уравнения Максвелла стараются свести к известным формам дифференциальных уравнений.

Рассмотрим гармонический электромагнитный процесс. Запишем уравнения Максвелла для комплексных амплитуд:

(1)

Уравнения гельмгольца в комплексной форме

Тема 5. волновые уравнения для векторов ЭМП

Уравнения гельмгольца в комплексной форме

Электродинамические потенциалы гармонического поля

Рекомендуемые файлы