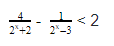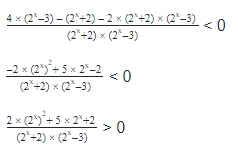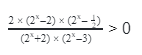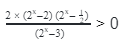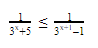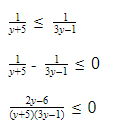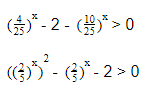Уравнения и неравенства 10 класс с решениями

«Решение неравенств». 10-й класс

Разделы: Математика

Класс: 10

Цели:

1. Систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения рациональных неравенств.
2. Содействовать развитию математического мышления учащихся,умению комментировать,тренировать память.
3. Воспитание ответственного отношения к учебному труду,чувства товарищества и взаимопомощи.

Оборудование: интерактивная доска, раздаточный материал(разноуровневые карточки с практическими заданиями).

Структура урока:

1. Сообщение темы и цели урока (1 мин.)
2. Проверка домашнего задания (5 мин.)
3. Систематизация знаний и умений по пройденному материалу (10 мин.)
4. Инструктирование по выполнению заданий в группах (3 мин.)
5. Выполнение заданий в группах (15 мин.)
6. Проверка и обсуждение полученных результатов (8 мин.)
7. Постановка домашнего задания (2 мин.)
8. Подведение итогов урока (1 мин.)

Ход урока

I. Сообщение темы и цели урока.

Сегодня на уроке мы будем решать неравенства методом интервалов и методом замены переменных. Эпиграфом к сегодняшнему уроку будут слова Ньютона:“При изучении наукпримеры не менее поучительны,нежели правила” и слова Ломоносова: “Примеры учат больше,чем теория”.

II. Проверка домашнего задания.

На дом были даны неравенства. Проверьте ваше решение по интерактивной доске.

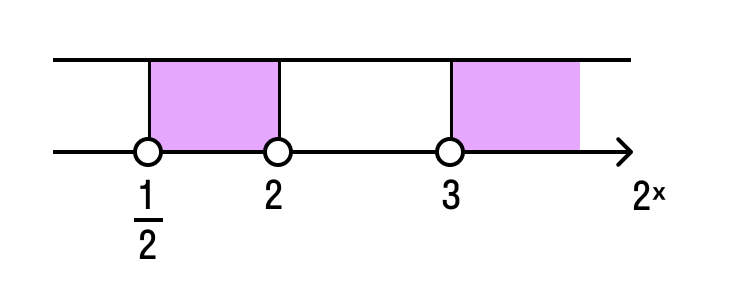
Отметим на числовой оси корни числителя и знаменателя.

Ответ: Є (-3; 1]

≥

Преобразуем исходное неравенство

– ≥ 0

≥ 0

≥ 0

≥ 0

Применим метод интервалов.

III. Систематизация знаний и умений по пройденному материалу.

Решим методом интервалов следующее неравенство. (Учитель на доске дает образец решения неравенств).

≥ 0

Рассмотрим функцию

1. Область определения функции f(x)находим из системы неравенств

Область определения: [-4; 3) U (3; 4]

2. Уравнение f (x) ═ 0 имеет корни: -4; 4; 3,5

Ответ: [-4; 3) U [3,5; 4]

Следующее неравенство решим методом замены переменных.

()² + 7 () +12 0

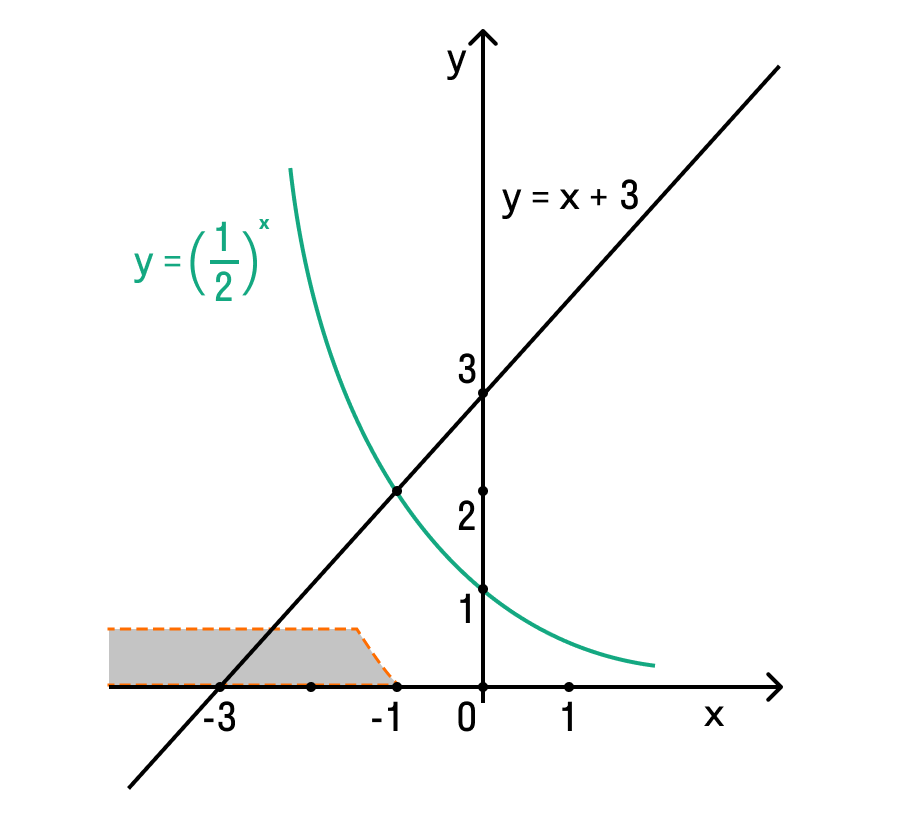
≤ 0

≥ 0

V. Выполнение заданий в группах.

VI. Проверка и обсуждение полученных результатов.

Проверьте по интерактивной доске решение работы.

Учащиеся осуществляют самопроверку и самооценку заданий. Получают разъяснения по возникающим при этом вопросам.

Ответы к рассмотренному варианту.

Воспользуемся методом интервалов, получим :

≤ 0

Замена

Тогда t-1 — ≤ 0

Показательные уравнения и неравенства с примерами решения

Содержание:

Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:

Уравнения такого вида принято называть показательными.

Решении показательных уравнений

При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.

Пусть

Каждому значению показательной функции соответствует единственный показатель s.

Пример:

Решение:

Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению

Пример:

Решение:

а) Данное уравнение равносильно (поясните почему) уравнению

Если степени с основанием 3 равны, то равны и их показатели:

Решив это уравнение, получим

Ответ:

При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.

Пример:

Решение:

а) Данное уравнение равносильно уравнению

Решая его, получаем:

Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. откуда находим

б) Разделив обе части уравнения на получим уравнение равносильное данному. Решив его, получим

Ответ:

При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.

Пример:

Решить уравнение

Решение:

Обозначим тогда

Таким образом, из данного уравнения получаем

откуда находим:

Итак, с учетом обозначения имеем:

При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.

Пример:

Решить уравнение

Решение:

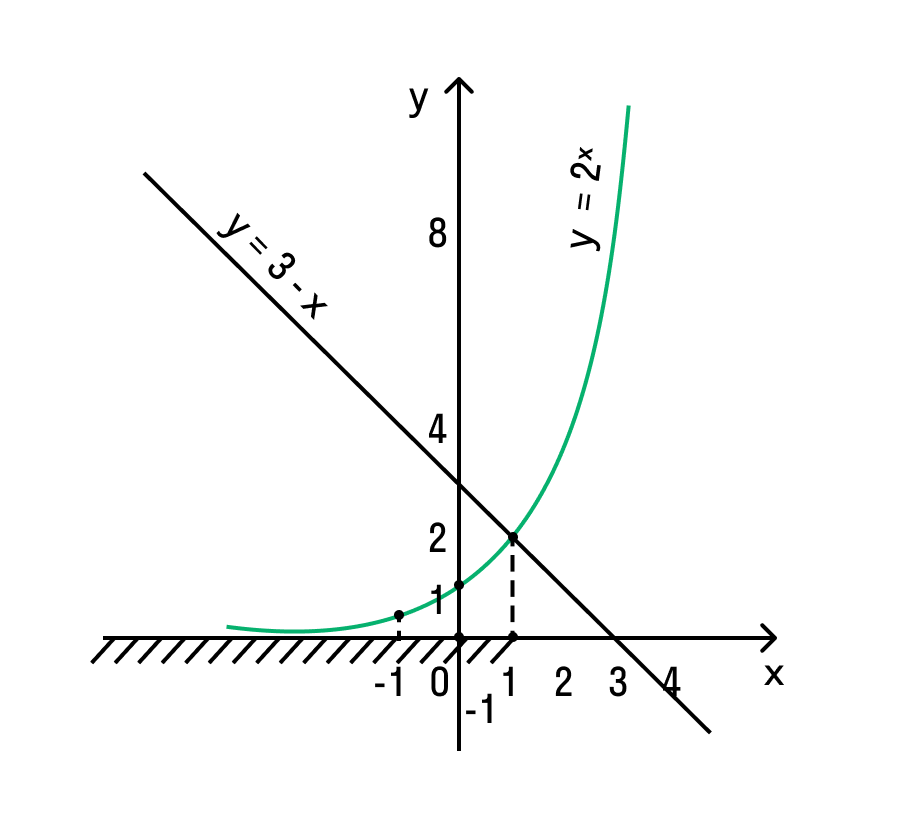
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).

Пример:

Решить уравнение

Решение:

Пример:

При каком значении а корнем уравнения является число, равное 2?

Решение:

Поскольку х = 2 — корень, то верно равенство

Решив это уравнение, найдем

Ответ: при

Показательные уравнения и их системы

Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:

Приведем методы решения некоторых типов показательных уравнений.

1 Приведение к одному основанию.

Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду . Отсюда

Пример №1

Решите уравнение

Решение:

Заметим, что и перепишем наше уравнение в виде

Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.

Пример №2

Решить уравнение

Решение:

Переходя к основанию степени 2, получим:

Согласно тождеству (2), имеем

Последнее уравнение равносильно уравнению 4х-19 = 2,5х.

2 Введение новой переменной.

Пример №3

Решить уравнение

Решение:

Применив тождество 2, перепишем уравнение как

Введем новую переменную: Получим уравнение

которое имеет корни Однако кореньне удовлетворяет условию Значит,

Пример №4

Решить уравнение

Решение:

Разделив обе части уравнения на получим:

последнее уравнение запишется так:

Решая уравнение, найдем

Значение не удовлетворяет условию Следовательно,

Пример №5

Решить уравнение

Решение:

Заметим что Значит

Перепишем уравнение в виде

Обозначим Получим

Получим

Корнями данного уравнения будут

Следовательно,

III Вынесение общего множителя за скобку.

Пример №6

Решить уравнение

Решение:

После вынесения за скобку в левой части , а в правой , получим Разделим обе части уравнения на получим

Системы простейших показательных уравнений

Пример №7

Решите систему уравнений:

Решение:

По свойству степеней система уравнений равносильна следующей

системе :Отсюда получим систему

Очевидно, что последняя система имеет решение

Пример №8

Решите систему уравнений:

Решение:

По свойству степеней система уравнений равносильна следующей системе: Последняя система, в свою очередь, равносильна системе:

Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем Подставив полученное значение во второе уравнение, получим

Пример №9

Решите систему уравнений:

Решение:

Сделаем замену: Тогда наша система примет вид:

Очевидно, что эта система уравнений имеет решение

Тогда получим уравнения

Приближенное решение уравнений

Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть . Тогда внутри этого отрезка существует хотя бы одно решение уравнения Дх)=0. Это означает, что существует такое (читается как «кси»), что

Это утверждение проиллюстрировано на следующем чертеже.

Рассмотрим отрезок содержащий лишь один корень уравнения .

Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности

1. вычисляется значение f(х) выражения
2. отрезок делится пополам, то есть вычисляется значение
3. вычисляется значение выражения f(х) в точке
4. проверяется условие
5. если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что (левый конец отрезка переходит в середину);
6. если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
7. для нового отрезка проверяется условие
8. если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.

Метод последовательного деления пополам проиллюстрирован на этом чертеже:

Для нахождения интервала, содержащего корень уравнения вычисляются значения

Оказывается, что для корня данного уравнения выполнено неравенство. Значит, данное уравнение имеет хотя бы один корень, принадлежащий интервалу (-1 -А; 1+А). Для приближенного вычисления данного корня найдем целые и удовлетворяющие неравенству

Пример №10

Найдите интервал, содержащий корень уравнения

Решение:

Поделив обе части уравнения на 2 , получим,

Так как, для нового уравнения

Значит, в интервале, уравнение имеет хотя бы один корень. В то же время уравнение при не имеет ни одного корня, так как,

выполняется. Значит, корень уравнения лежит в (-2,5; 0). Для уточнения этого интервала положим Для проверим выполнение условия

Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).

Нахождение приближенного корня с заданной точностью

Исходя из вышесказанного, заключаем, что если выполнено неравенство корень уравнения принадлежит интервалу

ПустьЕсли приближенный

корень уравнения с точностью . Если то корень лежит в интервале если то корень лежит в интервале . Продолжим процесс до нахождения приближенного значения корня с заданной точностью.

Пример №11

Найдите приближенное значение корня уравнения с заданной точностью

Решение:

Из предыдущего примера нам известно, что корень лежит в интервале

(-1; 0). Из того, что заключаем, что корень лежит в интервале (-0,5; 0).

Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если

Пусть

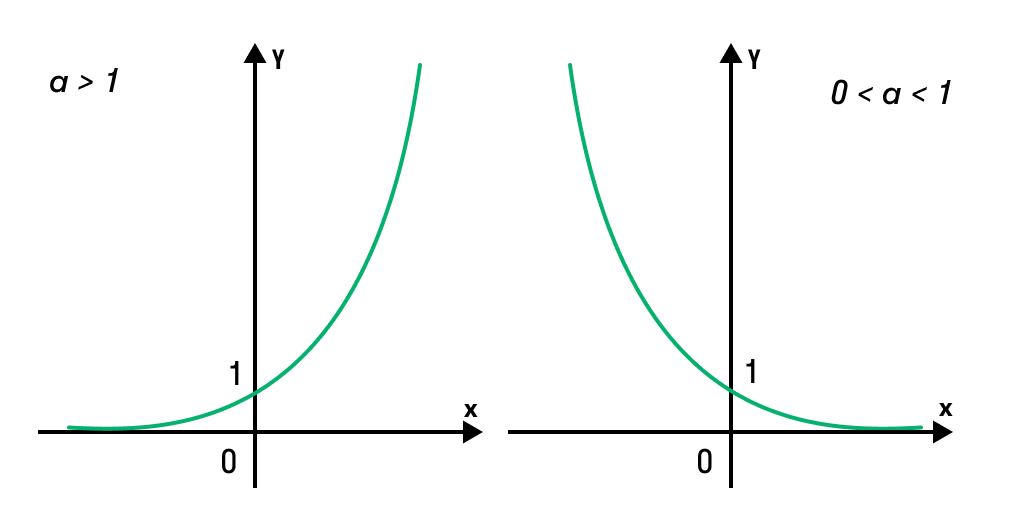
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Показательные неравенства

О чем эта статья:

10 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение показательных неравенств

Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: a f(x) > a g(x) , a f(x) g(x) .

Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.

Для изучения этой темы стоит повторить:

И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.

Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a x , где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.

При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2 -2 = 4, 2 -4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.

Для любых а и х верно неравенство a x > 0, т. е. показательная функция не принимает отрицательных значений.

Запишем следствие монотонности показательной функции в виде формул:

• a f(x) > a g(x) f(x) > g (x), когда функция возрастает, т. е. а > 1;
• a f(x) > a g(x) f(x)

Как решать показательные неравенства

Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости.

Допустим, у нас есть простейшее показательное неравенство:

Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:

Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:

Проверим, верно ли в таком случае х > 2.

0,5 3 = 0, 125 и т. д.

Как видите, на самом деле в этом случае х

Если а > 1, то a x > a n a > n, и при решении неравенства можно просто убрать одинаковые основания степени.

Если 0 x > a n a

Наконец, если рассмотреть случай, когда а х > 9

Логичное, на первый взгляд, предположение, что х > 2, не выдержит проверки, потому что:

Если продолжить этот ряд, знаки будут чередоваться, и наш корень будет попеременно то меньше, то больше 2. Поэтому для ясности всегда предполагается, что основание степени — положительное число.

Это были общие правила, а сейчас рассмотрим разные виды показательных неравенств и примеры с решениями.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Показательные неравенства, сводящиеся к простейшим

Решая показательные уравнения, вы наверняка первым делом исследовали их на возможность приведения к одинаковым основаниям или одинаковым степенным функциям. Так вот, с неравенствами можно делать то же самое! Помните лишь о смене знака, если основание степени меньше единицы. И да пребудет с вами сила. 😎

Попробуем на примере несложного показательного неравенства с разными основаниями.

Пример 1

Поскольку 3 больше 1, знак не меняем:

Показательные неравенства, сводящиеся к квадратным

Снова давайте вспомним, как аналогичный метод применялся к показательным уравнениям. Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.

Пример 1

Наименьший общий множитель в данном случае будет 3 х , обозначим его новой переменной у и перенесем все слагаемые в левую сторону.

(3 х ) 2 — 12 × 3 х + 27 х = у

y 2 — 12y + 27 х 1 х 2

Поскольку 3 > 1, мы не меняем знак.

1 2 x — 5 sinx + 2 2 — 5y + 2

Показательные неравенства, сводящиеся к рациональным

Как вы, наверное, помните из предыдущего курса алгебры, рациональные показательные неравенства — это такие, в которых левая и правая часть представляют собой дробно-рациональные функции. Метод их решения таков: нужно перенести все в левую часть, чтобы в правой остался лишь ноль, и привести к общему знаменателю. Далее решаем уравнение, отмечаем все корни на оси и применяем метод интервалов (если забыли, что это такое — повторите).

Важно помнить: если в числителе и знаменателе встретятся одинаковые множители с переменной, сокращать их нельзя.

Пример 1

Преобразуем неравенство указанным выше способом:

(обратите внимание, мы избавились от минуса в числителе и поменяли знак неравенства).

Поскольку выражение 2 х + 2 в любом случае будет больше нуля, мы можем смело его исключить из неравенства.

(2 х — 2) × (2 х — 1/2) × (2 х — 3) > 0

Пример 2

Обозначим 3 х через новую переменную y:

3 х = y, при условии что 3 х > 0.

Применим метод интервалов и получим:

Вернем на место нашу старую переменную:

Однородные показательные неравенства

Однородными называются такие показательные неравенства, где в каждом слагаемом сумма степеней одинакова.

Иногда такие выражения бывают очень длинными и запутанными, но не стоит этого пугаться. Практически все неравенства с однородными показательными функциями решаются по одному принципу: стараемся упростить выражение, разделив его на одночлен, а затем при необходимости делаем замену переменных.

Пример 1

4 х — 2 × 5 2х — 2 х × 5 х > 0

2 × 2 х — 2 × 5 2х — 2 х × 5 х > 0

В левой части неравенства мы видим однородные функции относительно 2 х и 5 х . Следовательно, можно разделить обе части на 2 2х или 5 2х . Выберем 5 2х , т. е. 25 х . В итоге у нас получится:

Если обозначить (2/5) х новой переменной y, получим квадратное неравенство:

Неравенства, решаемые графическим методом

Этот метод решения показательных неравенств — самый наглядный, и для многих он может показаться самым простым. Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Если бы мы имели дело с уравнением, эта точка стала бы корнем.

Но поскольку мы рассматриваем неравенства, нужно будет выделить искомую область. Для неравенства f(x) > g(x) это будет та область, где график функции f(x) находится выше.

Пример 1

2 х х и 3 — х, а также точка их пересечения.

Очевидно, что точкой пересечения является х = 1, при этом график функции 2 х ниже в области от -∞ до 1.

Пример 2

Начертим графики этих двух функций, чтобы найти точку пересечения.

Искомой точкой будет х = -1, а областью, где функция (1/2) х находится выше — диапазон от -∞ до -1.