Уравнения и неравенства с одной неизвестной

Неравенства с одной переменной

Линейное неравенство с одной переменной — это неравенство, которое можно привести к виду:

ax > b или ax 0, то, разделив обе части неравенства на a, получим:

Все возможные значения данных неравенств мы уже рассмотрели выше.

Если a = 0, тогда неравенство примет вид:

если b отрицательное число, в противном случае неравенство не имеет решений.

Во втором случае:

0 · x Пример 1. Решить неравенство и изобразить множество решений на координатной прямой:

Решение: Переносим -2 в правую часть:

Делим обе части неравенства на -8:

-8x : (-8) Пример 2. Решить неравенство и изобразить множество решений на координатной прямой:

Решение: Сначала раскрываем скобки:

Переносим 72 в правую часть, а 3y в левую и делаем приведение подобных слагаемых:

Делим обе части неравенства на коэффициент при неизвестном (на 3):

Отмечаем множество значений y на координатной прямой:

Решение линейных неравенств

О чем эта статья:

Основные понятия

Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

Неравенство — это алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Линейные неравенства — это неравенства вида:

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти все значения переменной, при которой неравенство верное.

Типы неравенств

1. Строгие — используют только больше (>) или меньше ( b — это значит, что a больше, чем b.
2. a > b и b > и

Линейные неравенства: свойства и правила

Вспомним свойства числовых неравенств:

1. Если а > b , то b а.
2. Если а > b и b > c, то а > c. И также если а b, то а + c > b+ c (и а – c > b – c).

Если же а b и c > d, то а + c > b + d.

Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

Если а d, то а – c b, m — положительное число, то mа > mb и

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа

Обе части можно умножить или разделить на одно отрицательное число, при этом знак неравенства поменять на противоположный.

1. Если а > b и c > d, где а, b, c, d > 0, то аc > bd.

Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Правила линейных неравенств

1. Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.

• 2x − 3 > 6 ⇒ 2x > 6 + 3 ⇒ 2x > 9.

1. Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется.

• Умножим обе части на пять 2x > 9 ⇒ 10x > 45.

1. Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный.

• Разделим обе части на минус два 2x > 9 ⇒ 2x : (–2) > 9 : (–2) ⇒ x
  

  Решение линейных неравенств

  Линейные неравенства с одной переменной x выглядят так:

  где a и b — действительные числа. А на месте x может быть обычное число.

  Равносильные преобразования

  Для решения ax + b , ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.

  Алгоритм решения ax + b , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.

  Рассмотрим пример: 0 * x + 5 > 0.

  Как решаем:

  • Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
  • Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.

  Метод интервалов

  Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

  Метод интервалов заключается в следующем:

  • вводим функцию y = ax + b;
  • ищем нули для разбиения области определения на промежутки;
  • отмечаем полученные корни на координатной прямой;
  • определяем знаки и отмечаем их на интервалах.

  Алгоритм решения ax + b , ≥) при a ≠ 0 с использованием метода интервалов:

  • найдем нули функции y = ax + b для решения уравнения ax + b = 0.

  Если a ≠ 0, тогда решением будет единственный корень — х₀;

  • начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
  • определим знаки функции y = ax + b на промежутках.

  Для этого найдем значения функции в точках на промежутке;

  если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если 0.

  Как решаем:

  В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,

  Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

  

  Определим знаки на промежутках.

  Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

  Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6

  Графический способ

  Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

  Алгоритм решения y = ax + b графическим способом

  • во время решения ax + b 0 определить промежуток, где график изображается выше Ох;
  • во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

  Рассмотрим пример: −5 * x − √3 > 0.

  Как решаем

  • Так как коэффициент при x отрицательный, данная прямая является убывающей.
  • Координаты точки пересечения с Ох равны (−√3 : 5; 0).
  • Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
  • Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

  Ответ: (−∞, −√3 : 5) или x

  Решение неравенств с одним неизвестным

  Линейные неравенства с одним неизвестным имеют вид:

  • A и B — заданные числа;
  • x — неизвестное.

  Число будет являться решением неравенства с одним неизвестным в том случае, если после его подстановки в неравенство вместо неизвестного х числовое неравенство будет верным.

  Например, одним из решений неравенства 5+x>4 будет x=1, т.к., 5+1>4 — это верное неравенство.

  Чтобы решить неравенство, следует найти все множество чисел, делающих неравенство верным или доказать, что никакое число не будет делать равенство верным, т.е., неравенство не будет иметь решений.

  Для решения неравенств пользуются свойствами неравенств:

  • при переносе слагаемого в другую часть неравенства, у переносимого слагаемого знак меняется на противоположный, при этом знак самого неравенства не изменяется;
  • обе части неравенства можно умножать или делить на одно и то же число, отличное от нуля, при этом, в случае умножения/деления на положительное число знак неравенства не изменяется; в противном случае, знак неравенства меняется на противоположный.

  Решение неравенств очень удобно представлять в графическом виде на числовой прямой.

  

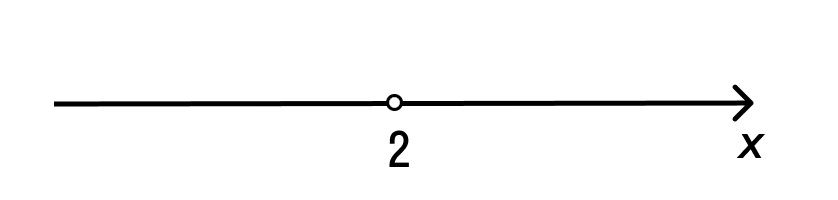
  На числовой прямой решением данного неравенства будет луч, начинающийся в точке 5 и идущий вправо, черный кружок, которым обозначено начало луча, говорит о том, что число 5 включается в число решений рассматриваемого неравенства.

  

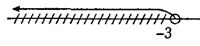
  На числовой прямой решением данного неравенства будет луч, начинающийся в точке -3 и идущий влево, белый кружок, которым обозначено начало луча, говорит о том, что число -3 не включается в число решений рассматриваемого неравенства.

  Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

  

  Код кнопки:
  Политика конфиденциальности Об авторе

  
  

  источники:

  http://skysmart.ru/articles/mathematic/linejnye-neravenstva

  http://prosto-o-slognom.ru/matematika/039-3-reshenie_neravenstv.html