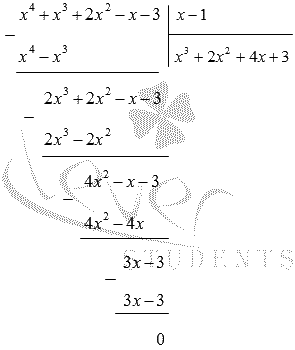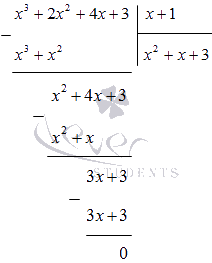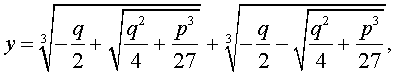Об уравнениях высших степеней
Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.
Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:

В этой статье я рассмотрю:
1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.
Кубические уравнения
Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:
Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:
В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.
Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.
Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.
Возвратные кубические уравнения
Возвратные кубические уравнения имеют вид:
Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:
Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.
Теорема Безу и схема Горнера
Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:
Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.
Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.
Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:
И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:
(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:
Возвратные биквадратные уравнения
Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:
В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:
Как видно, решать такие уравнения совсем не просто. Но я всё равно разберу и этот случай. Начинается решение с деления всего уравнения на x^2. Далее мы группируем, здесь я специально ввёл дополнительную строку для ясности. После этого мы совершаем хитрость, и вводим в первую скобку 2, которую мы сначала прибавляем, а после вычитаем, сумма всё равно не изменится, зато теперь мы можем свернуть эту скобку в квадрат суммы.
Уберём -2 из скобки, предварительно домножив его на a, после чего вводим новую переменную, t и получаем квадратное уравнение.
А теперь перейдём к примеру:
Основная часть так же как и в обобщённом алгоритме, делим на x^2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).
Область применения
В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.
Решение уравнений высших степеней
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
Методическое пособие на тему: «Алгебраические уравнения и неравенства высших степеней»
Данные методические рекомендации можно использовать в классах с профильным обучением или на факультативах. Они дают возможность понять прямую и обратную теорему Безу, способы решения уравнений третих и четвертых степеней. Развивают познавательную активность учащихся, воспитывают культуру устной и письменной речи
Просмотр содержимого документа
«Методическое пособие на тему: «Алгебраические уравнения и неравенства высших степеней»»
Алгебра и начало анализа в классах профильного обучения или на занятиях факультатива
Первые уроки по теме
«Алгебраические уравнения и неравенства высших степеней»
(Рассчитано на два спаренных урока)
Тема урока: Многочлен и его корни
Цель урока: Повторить основные сведения о многочлене, действия над многочленами (сложение, вычитание и умножение).
Ввести понятие корня многочлена, ознакомить с теоремой Безу, и обратной и обобщенной теоремой Безу; теоремой Виета для многочленов третьей и четвертой степеней, и последствий из теоремы Виета; развивать познавательную активность учащихся; воспитывать культуру устной и письменной речи.
Тип урока: урок усвоения новых знаний
Оборудование урока: цветные мелки, графопроектор, кодопозитивы.
Организационный этап (2 мин.)
II. Актуализация опорных знаний.
1. Что такое многочлен?
(Сумма нескольких одночленов)
2. Что значит записать многочлен в стандартном виде?
(Многочлен записано в стандартном виде, если все его члены — одночлены стандартного вида, и среди них нет подобных)
3. Как называется многочлен, содержащий два или три слагаемых?
(Двучлен и трехчлен)
4. Какие действия вы умеете выполнять с многочленами? (Сложение, вычитание, умножение)
5. Как добавить или вычесть два многочлена? (Поставить между многочленами знак «плюс» или «минус» и открыть скобки, учитывая правило открытия скобок перед которыми стоит знак «плюс» или «минус»).
6. Как умножить многочлен на многочлен?
(Чтобы умножить многочлен на многочлен нужно каждый член первого многочлена умножить на каждый член второго многочлена и полученные произведения добавить).
7. Как в общем виде записывается квадратный трехчлен? (aх2 + bх + с)
8. Что называется корнем квадратного трехчлена?
(Число, которое превращает квадратный трехчлен в равенство, равное нулю)
9. Как разложить квадратный трехчлен ах2 + bх + с на множители? (aх2 + bх + с = а (х — х1) (х — х2), где х1 и х2 — корни трехчлена).
10. Какое уравнение называется квадратным? (Квадратным уравнением называется уравнение вида ах2 + bх + с = 0, где а ≠ 0, b и с — любые числа, х — переменная).
11. Записать алгоритм нахождения решений квадратного уравнения, и сводного квадратного уравнения.
(Ответ на кодопозитиве № 1)
12. Теорема Виета для полного и приведенного квадратного уравнения.
(Ответ на кодопозитиве № 2)
ах 2 + вх + с = 0 х 2 + рх + q = 0
III. Сообщение темы, цели урока, места урока в теме.
IV. Мотивация учебной деятельности учащихся.
Учитель: Алгебра долго раскрывалась как наука о решения уравнений, прежде всего уравнений вида:
Мы повторили формулы решений квадратных уравнений.
В XVI — XVII возрасте были получены аналогичные, но более громоздкие формулы для уравнений третьей и четвертой степени.
Вот как выглядит, например знаменитая формула Кардано для решения уравнения у 3 + ру + q = 0.
Корни многочленов степени выше четвертой, как правило, не могут быть выражены формулами, в которые входят такие операции над коэффициентами многочлена, как сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Это было доказано в 1823 году норвежским математиком Галуа (1811 — 1832.) И положило конец многократным попыткам решить в общем виде уравнения пятой степени.
V. Восприятие и осознание учениками нового материала.
Учитель: Основными способами решения уравнений высших степеней два: разложение на множители и введения новой переменной.
Сначала рассмотрим произвольный многочлен n-ной степени в стандартной форме
Р(х) = а0х n + а1 х n-1 + . а n-1х + аn а0 — старший коэффициент, аn — свободный член. Важно знать, что многочлен от одной переменной с коэффициентом, равным единице, называется нормированным. Произведение нормированных многочленов является нормированным многочленом.
Запишем в тетрадях:
Определение 1. Число а называют корнем многочлена Р (х), если Р (а) = 0
Теорема Безу. Остаток от деления многочлена Р (х) на двучлен х — а равно Р (а), то есть Р(х) = (х – а)Q (х) + r
Обратная теорема Безу. Если число а является корнем многочлена Р (х), то этот многочлен делится на х — а без остатка.
Обобщенная теорема Безу. Если многочлен Р (х) имеет попарно различные корни а1 , а2, . аn , то он делится без остатка на произведение (х — а1)(х — а2) . (х – аn)
Последствия. Многочлен степени n имеет не более n различных корней.
Теорема Виета для трехчлена и многочлена четвертой степени.
Используются таблицы и кодопозитивы.
Нужно помнить, что, если многочлен Р (х) делится без остатка на (х – а) к , но не делится без остатка на (х – а) к+1 , то говорят, что число а — корень кратности для Р (х). Например: (х +4) 3 (х – 5) 2 (х + 1)(х + 2) получили многочлен Р (х), для которых число — 4 корень кратности три, число 5 — корень кратности два, а — 1 и -2 — корни кратности один.
VI. Закрепление и осмысление изученного материала.
Учитель рассматривает у доски пример №1 на деления многочлена на многочлен, подчеркивая, что это можно выполнить «углом», как это выполняется для целых чисел.
Разделить многочлен Р(х) = 2х 4 — 2 х 3 + х 2 + 4х + 5 на тричлен х 2 + х +2
2х 4 — 2 х 3 + х 2 + 4х + 5∟ х 2 + х +2
Значит, 2х 4 — 2 х 3 + х 2 + 4х + 5 = (х 2 + х +2)( 2 х 2 – 4х + 1) +11х +3
Ученик у доски выполняет пример № 2.
Разделить Р(х) = х 4 — 4х 3 + 6х 2 — 7х + 2 на тричлен х 2 — х — 2
х 4 — 4х 3 +6 х 2 — 7х + 2∟ х 2 — х — 2
х 4 — 4х 3 +6 х 2 — 7х + 2 = (х 2 — х – 2)( х 2 – 3х + 1)
Обсуждаем, что нового учащиеся узнали на уроке.
VIII. Задачи урока: составить план к материалу, записанному на уроке.
Разделить многочлен Р(х)=х 4 -2х 3 +х 2 -3х+5 на двочлен х 2 – 3х
(два ученика воспроизводят решение на прозрачной пленке)
Самостоятельная работа выполняется на отдельных листочках.
Каждому ученику раздается карточка с одним из вариантов.
Учащимся с высоким уровнем достижений -вариант №1 и №2. Работа проверяется учителем после уроков (каждый учащийся работает в индивидуальном режиме).
Вариант № 1. Выполнить деление многочлена на многочлен:
7х 4 — 4х 3 +3 х 2 — 10х + 4 на х- 5
Вариант № 2. Выполнить деление многочлена на многочлен:
3х 4 — 5х 3 +2х 2 + 7х — 1 на х + 2
Вариант № 3. Выполнить деление многочлена на многочлен:
2х 4 — 7х 3 +10х — 8 на х — 4
Вариант № 4. Выполнить деление многочлена на многочлен:
х 4 — 4х 3 +7х — 9 на х + 1
Подготовить рефераты на тему:
1. Прямая и обратная теорема Виета и ее применение.
2. Теорема Безу и ее следствия.
3. Многочлены и их свойства.
4. Нестандартные методы решения некоторых типов уравнений и неравенств.
1. И. Глейзер «История математики в школе»
2. М. Л. Галицкий «Углубленное изучение алгебры и математического анализа»
3. И. В. Виленкин «Алгебра и математический анализ. 10 класс»
4. И. Ф. Шарыгин «Факультативный курс по математике. 10 класс». (Решение задач)
5. М. И. Сканави «Сборник задач по математике»
Урок № 3, № 4 (рассчитано на два спаренные уроки)
Тема урока: Разложение многочлена на множители. Самостоятельная робота
Цель урока: 1) формировать умения и навыки при нахождении корней многочленов различными способами: используя практические выводы из теоремы Виета и обратную теорему Безу, схему Горнера и метод неопределенных коефициентов. усовершенствовать деления многочлена на многочлен «углом».
2) развивать в учащихся такие качества, как самостоятельность, творчество и инициативу, формирование у учащихся адекватной самооценки;
3) воспитывать настойчивость и усердие в работе.
Тип урока: урок формирования умений и навыков учащихся.
Оборудование урока: цветные мелки, комплект индивидуальных досок, графопроектор.
I. Организационный момент
II. Проверка домашнего задания.
III. Актуализация опорных знаний
IV. Анализ самостоятельной работы, проведенной на предыдущем уроке.
V. Сообщение темы, цели урока, места урока в теми.
VI. Мотивация учебной деятельности учащихся.
VII. Восприятие и осознание учениками нового материалу.VИИИ. Закрепление нового материала.
IХ. Самостоятельная робота.
Х. Итог урока. Сообщение домашнего завдання.
I. Организационный момент (2 мин.)
II. Проверка домашнего задания. 1. Верность выполнения домашних упражнений проверяется с помощью графопроектора. На прозрачной пленке записан пример, выполненный двумя учащимися.
Разделить многочлен х 4 — 2х 3 + х 2 — 3х + 5 на х 2 — 3х
х 4 — 2х 3 + х 2 — 3х + 5∟ х 2 -3 х
Имеем х 4 — 2х 3 + х 2 — 3х + 5 = ( х 2 — 3х)( х 2 + х +4) +9х +5
Зачитать план теоретического материала, записанный на предыдущем уроке. Образец плана может быть таким:
а) Как записывается произвольный многочлен n-й степени в стандартной форме?
б) Какой многочлен называется нормированным?
в) Дать определение корня многочлена.
г) Сформулировать теорему Безу, обратную теорему Безу и обобщенную теорему Безу
д) Последствия теоремы Безу и теоремы Виета (Ученики обсуждают ответ на вопрос плана, образовав «карусель», объединившись в группы по четыре ученика)
III. Актуализация опорных знань.
Тренировочные упражнения. (Тренировочные упражнения подготовлены учителем перед уроком на обратной части доски.
Ответ ученики записывают на индивидуальных досочках) .
Дан многочлен Р(х) =3 х 6 — 2х 5 + х 3 — 2х + 7
а) старший коэффициент (3)
б) свободный член (7)
в) степень многочлена (6)
г) делители свободного члена (+ 1; + 7)
д) делители старшего коэффициента (+ 1; + 3)
ж) возможные рациональные корни многочлена (+ 1; + 7/3)
Разложить квадратный трехчлен на множители, используя теорему Виета
х 2 -7 х + 12 = (х+3)(х+4)
х 2 — х – 12 = (х+4)(х – 3)
х 2 + х – 12 = (х – 4)(х + 3)
х 2 + 7 х +12 = (х – 3)(х – 4)
IV. Анализ самостоятельной работы, проведенной на предыдущем уроке.
Учитель демонстрирует кодопозитивы, на которых показано деления многочлена на многочлен «углом» .
7х 4 — 4х 3 + 3х 2 — 10х + 4∟ х – 5
7х 4 — 35х 3 7х 3 + 31х 2 + 158 х + 780
Значит, 7х 4 — 4х 3 + 3х 2 — 10х + 4 = (х – 5)( 7х 3 + 31х 2 + 158 х + 780) + 3904
Имеет смысл подчеркнуть, что если верно выполнено деления, то остаток от делений равно Р (5).
Проверим: Р (5) = 7 ∙ 625 — 4 ∙ 125 + 3 ∙ 25 — 10 ∙ 5 + 4 = 3904
3х 4 — 5х 3 + 2х 2 + 7х — 1 ∟ х + 2
3х 4 + 6х 3 3х 3 — 11х 2 + 24х — 41
Значит, 3х 4 — 5х 3 + 2х 2 + 7х — 1 = (х + 2)( 3х 3 — 11х 2 + 24х — 41) + 81
Проверка остатка Р (-2) = 3 ∙ 16 + 5 ∙ 8 + 2 ∙ 4 – 7 ∙ 2 – 1 = 81
2х 4 — 7х 3 + 10х — 8 ∟ х — 4
2х 4 — 8х 3 2х 3 + х 2 + 4х + 26
2х 4 — 7х 3 + 10х — 8 = (х – 4)( 2х 3 + х 2 + 4х + 26) + 96
Проверка остатка Р(4) = 2 ∙ 256 – 7 ∙ 64 + 10 ∙ 4 – 8 = 96
х 4 — 4х 3 + 7х — 9 ∟ х +1
х 4 — 4х 3 + 7х — 9 = (х + 1)( х 3 — 5х 2 + 5х + 2) – 11
Проверка остатка Р( — 1) = 1+4 – 7 – 9 = — 11
V. Сообщение темы, цели урока, места урока в теми
VI. Мотивация учебной деятельности учащихся.
Одним из способов решения уравнений высших степеней — способ разложения на множители многочлена, стоящего в левой части уравнения.
VII. Восприятие и осознание учениками нового материалу.
Учитель: Как разложить квадратный трехчлен на множители, мы уже изучили. Пусть требуется разложить на множители с целыми коэффициентами многочлен
Р(х) =2х 4 — 7х 3 — 3х 2 + 5х – 1
Напомним выводы из теоремы Виета:
а) корни многочлена с первым коэффициентом, равным единице, являются делителями свободного члена
б) корни многочлена общего вида могут быть дробными: числитель является делителем свободного члена, а знаменатель — первого коефициента
Значит: ищем цели корни среди делителей свободного члена: + 1.
Подходит — 1 Р (1) = 2 — 7 — 3 + 5 — 1 = — 4 Р (1) = 2 + 7 — 3 — 5 — 1 = 0
Учитель: обратите внимание, что число 1 является корнем многочлена, тогда и только тогда, когда сумма его коэффициентов равна нулю. Если число — 1 является корнем многочлена необходимо и достаточно, чтобы сумма его коэффициентов, стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах.
Первый способ, деление многочлена на многочлен «углом» .
Таким образом, делим
Р(х)= 2х 4 — 7х 3 — 3х 2 + 5х — 1 на х + 1
2х 4 — 7х 3 — 3х 2 + 5х — 1 ∟ х + 1
2х 4 + 2х 3 2х 3 — 9х 2 + 6х — 1
Р(х) = (х + 1)( 2х 3 — 9х 2 + 6х — 1)
Ищем целые корни кубического многочлена среди делителей его свободного члена: + 1.2 — 9 + 6 — 1 ≠ 0 — 2 — 9 — 6 — 1 = — 18 ≠ 0
Вычисления показали, что целых корней нет. Так как старший коэффициент многочлена не равен 1, то многочлен может иметь дробные рациональные корни. Дробными корнями могут быть только числа — ½; ½.
Подходит ½ ; 2 ∙ 1/8 – 9 ∙ ¼ + 6 ∙ ½ — 1 = ¼ — 9/4 + 3 – 1 = -2 + 3 – 1 = 0
2х 3 — 9х 2 + 6х — 1 ∟ х + 1
Таким образом, имеем:
Р(х) = (х + 1)(х – ½ )( 2х 2 — 8х+2) = (х + 1)(2х – 1)(х 2 — 4х+1)
трехчлен х 2 — 4х+1 на множители с целыми коэффициентами НЕ разлаживается.
Ответ: Р(х) = (х + 1)(2х – 1)(х 2 — 4х+1)
Второй способ-по схеме Горнера.
Пример 2. Разложить многочлен Р (х) на множители по схеме Горнера
Р(х) =х 4 — 2х 3 — 13х 2 + 14х + 24
Алгоритм нахождения корней многочлена:
а) записать делители свободного члена + 1; + 2; + 3; + 4; + 6; + 12; + 24
б) записать делители первого коэффициента + 1
в) записать возможные рациональные корни + 1; + 2; + 3; + 4; + 6; + 12; + 24.
г) способом подстановки найдем два корня, этого достаточно, чтобы получить в остатка квадратный тричлен.
Р(1) = 1 – 2 – 13 + 14 + 24 ≠ 0
Р( — 1) = 1+2 – 13 – 14 + 24 = 0
Р(2) = 16 – 2 ∙ 8 – 13 ∙ 4 + 14 ∙ 2 + 24 = 0
Составляем схему. В первой строчке этой таблицы записаны коэффициенты многочлена Р (х). Во второй строчке получаются коэффициенты доли и остаток. Старший коэффициент части равен старшему коэффициенту делимого. Если заполнено несколько ячеек второй строчки, то следующая пустая ячейка заполняется так: берут то число, стоящее над ним первой строчки и добавляют к нему произведение корня и предыдущего элемента второй строчки. В последний ячейке второй строки под свободным членом получается остаток от деления.
http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/
http://multiurok.ru/files/mietodichieskoie-posobiie-na-tiemu-alghiebraichies.html