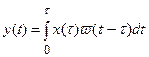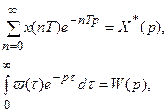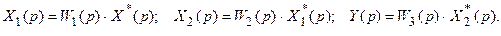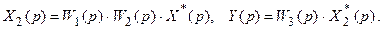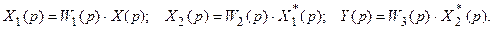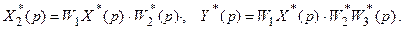Уравнения и передаточные функции разомкнутых импульсных систем

Передаточные функции импульсных СУ

1. Уравнения и передаточные функции импульсных разомкнутых систем

Рассмотрим импульсную систему (рис. 19.1). По аналогии с интегралом сверки для непрерывных систем

для импульсной системы можно записать

,

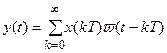
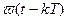
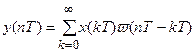
где — импульсная переходная функция приведенной непрерывной части (или просто непрерывной части). Для решетчатой функции будем иметь

,

а после z-преобразования этого выражения получаем

.

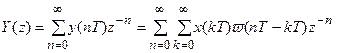
Рис. 19.1. Разомкнутая импульсная САУ

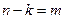
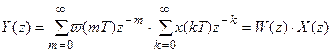
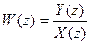
Подстановка позволяет получить

.

.

Это выражение по своей форме совпадает с выражением для передаточной функции непрерывной системы, только здесь рассматривается при нулевых начальных условиях отношение z-преобразований выходного Y(z) и входного сигналов X(z) дискретной системы.

Такую передаточную функцию называют z-передаточной функцией или импульсной передаточной функцией системы. Эта передаточная функция рассматривается только для дискретных сигналов, если же сигналы непрерывные, то фиксируются их значения только для дискретных моментов времени, кратных периоду прерывания сигнала в системе.

Выражение для z-передаточной функции может быть получено и по-другому – с использованием свойств идеального импульсного элемента.

Действительно, непрерывный сигнал на выходе системы (рис. 19.1) можно записать в виде

.

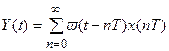
Преобразуем по Лапласу это уравнение:

.

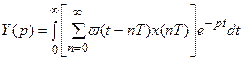
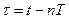
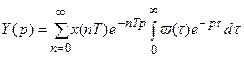
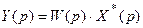
После замены будем иметь

.

. (19.1)

Полученное выражение (19.1) показывает, что если на входе непрерывной части действует дискретный сигнал x * (t), то изображение по Лапласу непрерывного выходного сигнала Y(p) будет определяться произведением передаточной функции непрерывной части W(p) на дискретное преобразование Лапласа от входного сигнала X * (p).

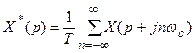
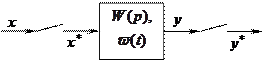Далее находим выражение для дискретного преобразования выходного сигнала на основании свойства идеального импульсного элемента. Эта процедура равносильна установке дополнительного ключа на выходе рассматриваемой системы (рис. 19.2).

Рис. 19.2. Разомкнутая импульсная САУ с дискретным выходом.

.

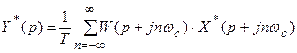
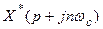
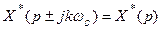
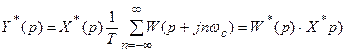
Поскольку функция периодическая и выполняется условие , можно записать

. (19.2)

Таким образом, при дискретном преобразовании Лапласа произведения непрерывного преобразования Лапласа на дискретное преобразование Лапласа некоторых функций (19.1) получаем произведение дискретных преобразований этих функций (19.2). Полученное свойство дискретного преобразования Лапласа весьма упрощает процесс определения передаточных функций дискретных систем.

На рис. 19.3 показаны варианты структурных схем разомкнутых импульсных систем с различными числом и местами включения импульсных элементов. Требуется определить z-преобразованиевыходного сигнала систем и их передаточные функции.

а)

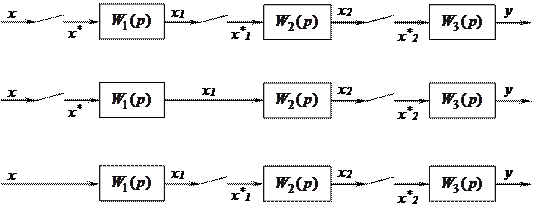
Рис. 19.3. Структурные схемы разомкнутых импульсных САУ.

Для системы (рис. 19.3,а) можно записать следующие уравнения:

Подвергнув эти уравнения дискретному преобразованию Лапласа и исключив промежуточные переменные, находим связь между входным и выходным сигналами этой системы:

.

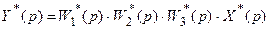
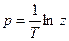
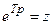
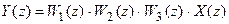
Для перехода к z-преобразованию делаем подстановку , поскольку . В результате получаем

,

а для z-передаточной функции имеем

.

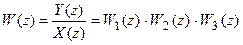
Для системы (рис. 19.3,б) справедливы следующие зависимости:

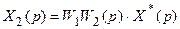
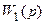
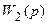
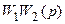
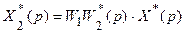
Рассмотрим первое из этих уравнений. Его можно записать , где условно обозначим произведение непрерывных преобразований Лапласа и через . Теперь найдем дискретное преобразование Лапласа

.

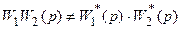
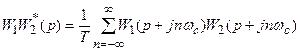
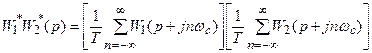
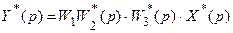
Следует иметь в виду, что . Действительно,

,

.

.

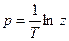
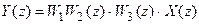
Путем подстановки переходим к z-преобразованию

,

z-передаточная функция системы имеет вид

.

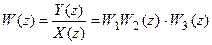
Рассмотрим систему, изображенную на рис. 19.3,в. Для нее можно записать следующие уравнения:

Из первого уравнения находим 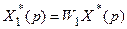, далее получаем

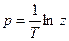
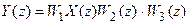
После подстановки переходим к z-преобразованию:

.

В это выражение z-преобразование входного сигнала входит в неявном виде, поэтому z-передаточная функция для такой системы не может быть получена.

Лекция 3 — Уравнения и передаточные функции

Уравнения и передаточные функции разомкнутых импульсных систем.

1. Эквивалентная схема разомкнутой импульсной системы.

2. Уравнения разомкнутой импульсной системы.

3. Передаточная функция разомкнутой импульсной системы.

1. Эквивалентная схема разомкнутой импульсной системы.

Рассмотрим простейшую разомкнутую импульсную систему, со­стоящую из амплитудно-импульсного элемента и непрерывной части. Импульсный элемент может быть представлен в виде последователь­ного соединения идеального импульсного элемента и экстраполя­тора. Таким образом, импульсная система всегда может быть при­ведена к соединению ИИЭ и непрерывных звеньев, как это по­казано на рис.8.

При таком представлении используют понятие приведенной непрерывной части (ПНЧ), состоящей из собственно непрерывной части, последовательно соединенной с формирующим звеном ИЭ. Передаточная функция ПНЧ определяется выражением

.

ПНЧ также может исчерпывающим образом характеризоваться своей весовой функцией

Рекомендуемые файлы

2. Уравнения разомкнутой импульсной системы.

В соответствии с определением ИИЭ имеем

. (6)

Выходной сигнал в силу свойства линейности можно рассматривать как сумму реакций приведенной непрерывной части на модулированную последовательность d–функций (6). В соответствии с известной формулой для непрерывных линейных систем при нулевых начальных условиях получим

или с учетом формулы (6)

(7)

Так как весовая функция , рассматриваемая по аргументу t, удовлетворяет условию

Таким образом, оба сомножителя под знаком интеграла отличны от нуля только при выполнении условия . Для этих значений к в силу фильтрующего свойства d-функции найдем

(8)

Так как имеет смысл рассматривать только значения к, не превосходящие n, то в выражении (7) можно заменить верхний предел суммирования. Окончательно с учетом формулы (8) получим

(9)

При этом в дискретные моменты времени t=nT , n=0,1,… будем иметь

. (10)

Уравнение (10) представляет собой уравнение импульсной системы во временной области, позво­ляющее определить выходной сигнал системы при известном вход­ном воздействии.

3. Передаточная функция разомкнутой импульсной системы.

3апишем теперь уравнения разомкнутой системы в изображени­ях. Применим к зависимости (10) Z-преобразование, С учетом свойств Z-преобразования найдем

, (11)

Определим Z -передаточную функцию импульсной системы как отношение Z -преобразования выходной величины к Z -преоб­разованию входной величины при нулевых начальных условиях:

.

Из уравнения (11) следует, что Z -передаточная функ­ция разомкнутой импульсной системы равна Z -преобразованию дискретной весовой функции w[nT] ПНЧ. т.е.

. (12)

Формула (12) используется при вычислении Z -передаточных функ­ций разомкнутых импульсных систем.

Иногда возникает необходимость определить реакцию системы в смещенные дискретные моменты времени . Подставив в зависимость (9) , получим

Диагностика осложнений острого панкреатита — лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

(13)

Перейдя к уравнению в изображениях, найдем

(14)

Здесь изображения соответствуют модифицированному Z-преобразованию решетчатых функций , . Уравнению (14) соответствует передаточная функция

,

cвязывающая модифицированное Z-преобразование выходного сигнала и обычное Z-преобразование входной переменной. При изменении параметра от 0 до 1 зависимости (13), (14) позволяют определить значение выходной величины в любой промежуточный момент времени.

Конспект лекций (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6

Тульский государственный университет

Кафедра «Системы автоматического управления»

ИМПУЛЬСНЫЕ И ЦИФРОВЫЕ

направления 550200 “Автоматизация и управление”

“Системы автоматического управления летательными аппаратами”

очной формы обучения

Общие сведения о дискретных автоматических системах. 6

1. Квантование по времени и по уровню. 6

2. Виды импульсной модуляции. 7

3. Импульсные и цифровые методы в системах автоматического управления 9

Импульсный элемент и его уравнения. 11

1. Предварительные замечания 11

2. Амплитудно-импульсный элемент и его эквивалентное представление. 11

3. Идеальный импульсный элемент и его математическое описание. 13

4. Формирующее звено и его математическое описание. Экстраполятор нулевого порядка. 13

Уравнения и передаточные функции разомкнутых импульсных систем. 15

1. Эквивалентная схема разомкнутой импульсной системы. 15

2. Уравнения разомкнутой импульсной системы. 15

3. Передаточная функция разомкнутой импульсной системы. 16

Вычисление Z-передаточных функций. 18

2. Учет экстраполятора при вычислении Z — передаточных функций. 19

3. Пример вычисления Z –передаточной функции. 21

Уравнения и передаточные функции замкнутых импульсных систем. 23

1. Уравнения и передаточные функции простейшей замкнутой импульсной системы. 23

2. Структурные преобразования в импульсных системах. 25

Частотные характеристики дискретных систем. 29

1. Определение установившейся реакции импульсной системы на дискретный гармонический сигнал. 29

2. Частотные характеристики дискретных систем. 30

3. Свойства частотных характеристик импульсных систем. 31

Вычисление частотных характеристик дискретных систем. 33

1. Псевдочастотные характеристики импульсных систем. 33

2. Методы построения частотных и псевдочастотных характеристик дискретных систем. 34

Частотные свойства импульсных систем. 37

1. Прохождение непрерывного гармонического сигнала через дискретную систему. 37

2. Спектры сигналов в дискретной системе. 38

Устойчивость импульсных систем. 41

1. Понятие устойчивости. 41

2. Условия устойчивости импульсных систем. 41

Алгебраические критерии устойчивости импульсных систем. 44

1. Переход к алгебраическим критериям устойчивости непрерывных систем. 44

2. Критерий Шура-Кона. 45

Частотные критерии устойчивости импульсных систем. 47

1. Аналог критерия Михайлова. 47

2. Анализ устойчивости с помощью критерия Найквиста. 48

3. Анализ устойчивости импульсной системы с помощью ЛАФПЧХ. 50

Математическое описание импульсных систем с помощью пространства состояний. 55

1. Пространство состояний дискретной системы 55

2. Уравнения состояния дискретных систем 56

Выбор переменных состояния дискретной системы. 60

1. Способ прямого программирования. 60

2. Способ параллельного программирования. 61

3. Способ последовательного программирования. 63

Анализ дискретных систем с использованием пространства состояний. 64

1. Вычисление Z –передаточной функции системы. 64

2. Вычисление Z – передаточной функции дискретной системы управления электродвигателем. 65

Анализ дискретных систем с использованием пространства состояний (продолжение). 67

1. Анализ устойчивости дискретных систем. 67

Определение переходных процессов при описании дискретных систем уравнениями состояния. 68

Описание импульсных систем с несколькими импульсными элементами с помощью пространства состояний. 71

1. Математическое описание синхронных импульсных систем с кратными периодами квантования ИЭ. 71

2. Пример составления математического описания импульсной системы. 72

Особенности вынужденных процессов в импульсных системах. 76

1. Свободный и вынужденный процессы в импульсных системах 76

2. Расчет вынужденных процессов с помощью моментов весовой характеристики 77

3. Процессы конечной длительности в импульсных системах. 77

Анализ вынужденных процессов в импульсных системах. 79

1. Вынужденные процессы при степенных входных воздействиях. 79

2. Установившиеся ошибки при типовых входных сигналах. 80

3. Коэффициенты ошибок дискретной системы 82

Синтез цифровых автоматических систем. 85

1. Основные схемы коррекции цифровых систем. 85

Синтез последовательных аналоговых регуляторов. 88

1. Общая последовательность синтеза. 88

2. Пример синтеза последовательного аналогового корректирующего устройства. 90

Синтез цифровых САУ с цифровыми регуляторами. 93

1. Синтез цифровых САУ с цифровыми регуляторами. 93

2. Некоторые вопросы реализации импульсных фильтров. 94

3. Реализация цифровых регуляторов в виде импульсных фильтров. 94

4. Реализация цифровых регуляторов на микроЭВМ. 95

Синтез ЦСУ с апериодическим переходным процессом. 99

1. Общие положения. 99

3. Общий случай синтеза системы с апериодическим переходным процессом. 100

Реализация аналогового прототипа с помощью цифрового фильтра. 103

1. Общие положения. 103

2. Реализация интегрирующих цифровых фильтров. 103

3. Пример нахождения цифрового фильтра, соответствующего данному прототипу. 104

Синтез алгоритма управления на основе решения обратной задачи динамики 106

1. Обзор задач динамики. 106

2. Задача аналитического построения замкнутой системы программного движения. 106

3. Синтез алгоритма управления на примере системы третьего порядка. 107

Лекция №1.

Общие сведения о дискретных автоматических системах

1. Квантование по времени и по уровню.

2. Виды импульсной модуляции.

3. Импульсные и цифровые методы в системах автоматического управления (САУ).

1. Квантование по времени и по уровню.

В непрерывных автоматических системах, изучавшихся в курсе «Основы ТАУ», сигналы, поступающие на входы и выходы элементов САУ, являются, как правило, непрерывными функция­ми времени. Однако во многих случаях оказывается выгодным пе­реход от непрерывного к дискретному способу представления и преобразования информации. Этот переход осуществляется дискре­тизацией непрерывного сигнала, т. е. заменой непрерывной функ­ций f(t) дискретными значениями f1 ,f2. fn, .. . Дискрети­зация (квантование) непрерывного сигнала может осуществлять­ся по времени, по уровню или и по времени и по уровню.

Дискретизация сигнала по времени состоит в замене не­прерывного сигнала (рис.1,а) дискретными значениями, взяты­ми в определенные, заранее заданные моменты времени. Обычно эти момента времени равноудалены друг от друга на величи­ну Т, которая называется интервалом квантования или перио­дом дискретности (рис.1,б). В этом случае последователь­ность

, n=1,2,3. , определяется формулой

Рис.1

Дискретизация по уровню предполагает замену непрерывно­го сигнала числовой последовательностью f1 , f2. fn. эле­менты которой могут принимать лишь заранее определенные, обычно равноотстоящие друг от друга значения (рис.1, в). Моменты времени, в которые происходит смена уровней, определяются видом непрерывного сигнала f(t) и заранее неизвестны.

Дискретизация и по времени и по уровню совмещает в себе изложенные выше два способа формирования последовательности ,n=1,2.. . При этом непрерывный сигнал заменяется дискретной последовательностью , n=1,2… взятой в заранее заданные моменты времени, и каждый элемент этой по­следовательности округляется до ближайшего к нему значения уровня из числа разрешенных (рис.1,г).

Обычно применяют следующую классификацию дискретных систем:

— импульсные системы, в которых осуществляется дискрети­зация хотя бы одной из переменных системы по времени;

— релейные системы, в которых осуществляется дискретиза­ция по уровню;

— цифровые системы, в которых осуществляется дискретиза­ция сигналов и по времени и по уровню.

Из приведенных трех типов дискретных систем релейные САУ обычно рассматриваются как непрерывные системы с разрывной нелинейностью. В данном курсе ограничимся изучением импуль­сных и цифровых систем, особенности динамики которых опреде­ляются дискретизацией по времени.

2. Виды импульсной модуляции.

При дискретизации по времени непрерывная функция заменя­ется своими дискретами, выделенными в определенные моменты времени. Однако на практике нельзя реализовать решетчатую функцию с бесконечно малым временем существования каждого выделенного значения. При конечном времени работы технических устройств получается последовательность импульсов определен­ной длительности, промодулированная выделенными дискретами непрерывной функции. В теории дискретных систем принято выде­лять импульсный элемент (ИЭ), осуществляющий дискретизацию по времени и модуляцию. В схемах импульсный элемент обозначают так, как показано на риc. 2.

Рис. 2

Таким образом, импульсный элемент порождает последовательность импульсов, параметры которых связаны со значениями не­прерывного сигнала в моменты квантования 0, Т,2Т,3Т (здесь и далее будем считать моменты квантования равностоящими друг от друга). В зависимости от того, какой параметр импульса определяется значениями выделенных дискрет, различают амплитудно-импульсную, широтно-импульсную и фазо-импульсную модуляции.

В случае амплитудно-импульсной модуляции амплитуда им­пульса постоянной длительности An определяется дискретой f[nT]

.

В частном случае линейной амплитудно-импулъсной модуляции

.

Этот случай иллюстрируется рис. 3,а.

Рис. 3

При широтно-импульсной модуляции (рис. 3,б) амплитуда импульсов постоянна, а их длительность (не превышающая интервала квантования) зависит от выделенных значений дискрет, т. е.

.

При фазо-импульсной модуляции амплитуда и ширина импуль­са постоянны, а величина f[nT] определяет его положение внутри интервала квантования (рис.3,в), т. е.

.

Отметим, что два последних вида импульсной модуляции принципиально нелинейны. Дискретизацию и по времени и по уровню можно рассматривать как амплитудно-импульсную модуляцию, когда в зависимости для An функция имеет вид, представленный на рис. 4. Таким образом, цифровые системы можно трактовать как один из типов нелинейных импульсных систем.

Линейные импульсные системы характеризуются наличием в своем составе импульсного элемента, осуществляющего линейную амплитудно-импульсную модуляцию.

Рис. 4

3. Импульсные и цифровые методы в системах автоматического управления

Дискретные системы автоматического управления играют важ­ную роль в современном приборостроении, технике управления и связи. Их преимуществами являются экономичность, высокие ди­намические характеристики, малый вес. Области их применения весьма разнообразны.

Важнейшим классом дискретных систем являются цифровые САУ. Первые результаты использования цифровых вычислительных машин (ЦВМ) в системах автоматического управления показали, что они обладают большой гибкостью и универсальностью по срав­нению с аналоговой техникой. Вследствие этого цифровые сред­ства управления стали широко применяться в САУ. Их использова­ние позволило решать качественно новые задачи управления, реа­лизовывать сложные алгоритмы управления, связанные с обработ­кой большого количества информации, которую трудно провести с помощью аналоговой техники. Усложнение алгоритма управления, реализуемого на базе аналоговой техники, неизбежно требует увеличения числа резисторов, конденсаторов и других элементов. В то же время аналогичное усложнение алгоритма управления в рамках цифровых систем приводит лишь к усложнению программы для ЦВМ. Цифровые системы обладают высокой помехоустойчивостью, так как сигналы в таких системах являются кодированными и пе­редаются практически без ошибок (за исключением ошибки, вно­симой квантованием по уровню). Использование ЦВМ в контуре управления позволяет применить методы нелинейного программиро­вания, оптимального управления, теории самонастраивающихся систем.

При учете квантования сигналов по уровню математическая модель цифровой САУ оказывается принципиально нелинейной и весьма сложной для исследования. Вследствие этого процесс про­ектирования таких систем обычно разделяется на два этапа. На первом этапе используется линейное приближение — линейная импульсная система. При этом не учитывается операция кванто­вания по уровню и производится линеаризация непрерывной части системы, если в этом есть необходимость. Использование линей­ных моделей цифровых САУ позволяет решать целый ряд важных вопросов их анализа и синтеза: исследовать зависимость показа­телей качества от параметров системы, проводить синтез алго­ритмов управления, определять требования к формирующей алго­ритм управления ЦВМ и т. д. В принципе, все исследование может заканчиваться выполнением только первого этапа.

На втором этапе исследования используется нелинейная математическая модель цифровой САУ. Она позволяет установить возможность возникновения незатухающих колебаний в системе, определить их параметры, область существования и т. д.

В данном курсе рассматривается динамика цифровых САУ на основе линейных математических моделей. При необходимости использования нелинейных математических моделей цифровых си­стем можно воспользоваться имеющейся к настоящему времени литературой.

Лекция № 2

Импульсный элемент и его уравнения

Амплитудно-импульсный элемент и его эквивалентное представление.

3. Идеальный импульсный элемент и его математическое описание.

4. Формирующее звено и его математическое описание. Экстраполятор нулевого порядка.

1. Предварительные замечания

Как и в непрерывных системах, исследование динамики дис­кретных систем может проводиться либо с использованием пере­менных состояния, либо с использованием входных и выходных переменных систем. В первом случае исследование обычно про­водят во временной области, рассматривая систему разностных уравнений и анализируя свойства ее решений. Этот подход и раз­работанные в его рамках методы являются весьма плодотворными. Они позволяют рассматривать нелинейные многомерные дискретные системы, проводить исчерпывающее исследование их свойств, решать задачи синтеза в различной постановке.

Во втором случае исследуют не весь набор переменных со­стояния, а лишь поведение некоторых величин, по изменению ко­торых и оценивается качество САУ — выходные переменные си­стемы. В задачу исследования может входить анализ зависимо­сти выходных переменных от входных величин, решение вопроса, как придать системе требуемые свойства по этим переменным и т. п. При этом для линейных импульсных систем наиболее простым и распространенным математическим аппаратом описания и исследования является аппарат дискретного преобразования Лапласа и Z — преобразования, позволяющий получить уравнение САУ в изображениях и найти дискретные передаточные функции.

Рассмотрим вопросы описания и исследования дискретных систем каждым из указанных методов. Начнем со второго подхо­да, когда для математического описания системы используются уравнения в изображениях и дискретные передаточные функции.

2. Амплитудно-импульсный элемент и его эквивалентное представление.

Простейшую импульсную систему можно представить в виде соединения импульсного элемента и непрерывной части. Рассмот­рим амплитудно-импульсный элемент (АИЭ). Импульсный элемент представляет собой устройство, на выходе которого в момент времени t=0,T, … nT, … наблюдается последовательность импульсов произвольной формы с амплитудами, пропорциональными дискретам входного сигнала x[nT]. Обозначение АИЭ в схемах и соответствующие при этом друг другу входной и выходной сигналы пока­заны на рис.5.

Рис. 5

При математическом описании ИЭ оказывается удобным поня­тие идеального импульсного элемента (ИИЭ). Под идеальным им­пульсным элементом будем понимать звено, выходная величина x*(t) которого представляет собой последовательность -функций с площадями, равными дискретам входной величины х[nT] . Пусть функция s(t) задает форму импульса на выходе ИЭ, соответству­ющего единичной дискрете входного сигнала, приложенной в мо­мент времени t=0 , в силу свойства линейности дискрете х[nТ] соответствует импульс

(1)

(сдвиг аргумента t на nT объясняется тем, что импульс возникает при t=nТ и не раньше). Определим реакцию на дис­крету x[nT] последовательного соединения ИИЭ и непрерывного звена c импульсной переходной функцией s(t) (см. рис.6). При этом .

Пройдя через непрерывное звено, дельта-функция в силу свойств импульсной переходной характеристики развернется в сигнал и, таким образом, на выходе цепочки получим функцию , совпадающую с функцией (1) .Отсюда следует, что импульсный элемент с произвольной формой импуль­са s(t) можно представить как последовательное соединение ИИЭ и непрерывного звена с импульсной переходной функцией s(t). Это непрерывное звено может быть также задано своей передаточной функцией s(p)=L[s(t)]. Линейное звено, определяющее форму импуль­са, называют также формирующим звеном, или экстраполятором, и обычно присоединяют его к непрерывной части системы. Таким об­разом, в линейной импульсной системе с одним ИЭ можно выделить идеальный ИЭ и непрерывную часть.

Рис. 6

3. Идеальный импульсный элемент и его математическое описание.

Рассмотрим идеальный импульсный элемент. В соответствии с определением уравнение, связывающее входной x(t) и выходной сигналы ИИЭ, имеет вид

, (2)

т. е. выходная переменная есть поcледовательность -функций, промодулированных входным сигналом. При этом

,

т. е. преобразование Лапласа выходной величины ИИЭ равно дис­кретному преобразованию Лапласа решетчатой функции x[nT]. Связь между изображениями непрерывной x(t) и решетчатой x[nT] функций устанавливается зависимостью

(3)

В итоге ИИЭ может быть описан зависимостями (2) или (3). Зависимость (2) устанавливает связь между входной x(t) и выходной переменными, зависимость (3) — между соответствующими изображениями.

4. Формирующее звено и его математическое описание. Экстраполятор нулевого порядка.

Формирующее звено порождает из -импульсов на выходе ИИЭ последовательность физических импульсов, характерную для данного устройства. Как отмечалось ранее, импульсная переходная функция формирующего звена s(t) (весовая функция) опреде­ляется формой импульса. Передаточная функция формирующего звена S(p) задается выражением

Например, если выходная последовательность импульсов имеет вид, представленный на рис.7, то передаточная функция формирующего звена будет

,

где k-коэффициент пропорциональности амплитуды выходного импульса и соответствующей дискреты входного сигнала.

Рис. 7

Если выходная величина ИЭ остается постоянной в течение всего интервала квантования Т, то формирующее звено называется экстраполятором нулевого порядка. Его передаточная функция имеет вид

(5)

Здесь и далее будем считать, что k=1 . В практике импульсного регулирования могут встречаться и другие формы выходных сигналов ИЭ, однако в САУ наиболее часто используются прямоугольные импульсы. Поэтому в дальнейшем ограничимся рассмотрением формирующих звеньев с передаточными функциями (4) или (5).

Лекция № 3

Уравнения и передаточные функции разомкнутых импульсных систем.

1. Эквивалентная схема разомкнутой импульсной системы.

2. Уравнения разомкнутой импульсной системы.

3. Передаточная функция разомкнутой импульсной системы.

1. Эквивалентная схема разомкнутой импульсной системы.

Рассмотрим простейшую разомкнутую импульсную систему, со­стоящую из амплитудно-импульсного элемента и непрерывной части. Импульсный элемент может быть представлен в виде последователь­ного соединения идеального импульсного элемента и экстраполя­тора. Таким образом, импульсная система всегда может быть при­ведена к соединению ИИЭ и непрерывных звеньев, как это по­казано на рис.8.

При таком представлении используют понятие приведенной непрерывной части (ПНЧ), состоящей из собственно непрерывной части, последовательно соединенной с формирующим звеном ИЭ. Передаточная функция ПНЧ определяется выражением

.

ПНЧ также может исчерпывающим образом характеризоваться своей весовой функцией

Рис. 8

2. Уравнения разомкнутой импульсной системы.

В соответствии с определением ИИЭ имеем

. (6)

Выходной сигнал в силу свойства линейности можно рассматривать как сумму реакций приведенной непрерывной части на модулированную последовательность d–функций (6). В соответствии с известной формулой для непрерывных линейных систем при нулевых начальных условиях получим

или с учетом формулы (6)

(7)

Так как весовая функция , рассматриваемая по аргументу t, удовлетворяет условию

Таким образом, оба сомножителя под знаком интеграла отличны от нуля только при выполнении условия . Для этих значений к в силу фильтрующего свойства d-функции найдем

(8)

Так как имеет смысл рассматривать только значения к, не превосходящие n, то в выражении (7) можно заменить верхний предел суммирования. Окончательно с учетом формулы (8) получим

(9)

При этом в дискретные моменты времени t=nT, n=0,1,… будем иметь

. (10)

Уравнение (10) представляет собой уравнение импульсной системы во временной области, позво­ляющее определить выходной сигнал системы при известном вход­ном воздействии.

3. Передаточная функция разомкнутой импульсной системы.

3апишем теперь уравнения разомкнутой системы в изображени­ях. Применим к зависимости (10) Z-преобразование, С учетом свойств Z-преобразования найдем

, (11)

Определим Z — передаточную функцию импульсной системы как отношение Z — преобразования выходной величины к Z — преоб­разованию входной величины при нулевых начальных условиях:

.

Из уравнения (11) следует, что Z — передаточная функ­ция разомкнутой импульсной системы равна Z — преобразованию дискретной весовой функции w[nT] ПНЧ. т. е.

. (12)

Формула (12) используется при вычислении Z — передаточных функ­ций разомкнутых импульсных систем.

Иногда возникает необходимость определить реакцию системы в смещенные дискретные моменты времени . Подставив в зависимость (9) , получим

(13)

Перейдя к уравнению в изображениях, найдем

(14)

Здесь изображения соответствуют модифицированному Z-преобразованию решетчатых функций , . Уравнению (14) соответствует передаточная функция

,

cвязывающая модифицированное Z-преобразование выходного сигнала и обычное Z-преобразование входной переменной. При изменении параметра от 0 до 1 зависимости (13), (14) позволяют определить значение выходной величины в любой промежуточный момент времени.

Лекция № 4

Вычисление Z-передаточных функций.

1. -преобразование дробно-рациональных функций.

2. Учет экстраполятора при вычислении Z — передаточных функций.

3. Пример вычисления Z –передаточной функции.

1. -преобразование дробно-рациональных функций.

Рассмотрим вычисление Z — передаточной функции простей­шего соединения (см рис 8 ). В соответствии с формулой (12) и свойствами Z -преобразования Z — передаточная функция w(z) может быть найдена по известной весовой функции ПНЧ w(t) или по ее передаточной функции W(p). Связь между передаточными функциями W(z) и W(p) задается — преобразованием с последующей заменой . Обозначим операцию выполнения — преоб­разования с заменой через . Тогда

(15)

Приведем таблицу -преобразования для некоторых часто встречающихся функций W(p) [l] .

,

,

Так как — преобразование обладает свойством линейно­сти, то в случае, если W(p) — дробно-рациональное выражение, вычисление Z — передаточных функций можно проводить следующим образом:

Передаточную функцию W(p) разложить на простейшие дроби