Регулярный режим теплопроводности
Регулярный режим теплопроводности
- Нормальная теплопроводность Охлаждение с течением времени однородной изотропной теплоты любой формы в среде с постоянной температурой и постоянным коэффициентом теплопередачи определяется дифференциальным уравнением теплопроводности. dtJdx = AV2 / (25-14) И граничные условия: (DIdn) n к o = — (a / X) ((σ / cp), (/) Xa = o // (x, y, r). Решение уравнения (25-14) с использованием / cp =
const показывает, что температура в любой точке тела изменяется экспоненциально. / —Оо — т. х 0 = 2А, е, (25-15) » = Я Где ft = to’-r- (cv \ At — это постоянная, которая зависит от формы тела и начального распределения температуры .- » Координатные функции, характеризующие изменение температуры в пространстве; / i — серия положительных Константа, представляющая приращение (τ1 xlt,
начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями. и описывается первым членом серии (25-15). ft = A ^ ge — «^. Из уравнения (25-17) нормальный режим теплопроводности Это связано с тем, что натуральный логарифм избыточной температуры ft в любой точке тела изменяется со
Вторая фаза охлаждения называется нормальным режимом Людмила Фирмаль
временем вдоль линейного заряда. «; — .. , Дифференцирование обеих сторон уравнения (25-17) по времени дает 1 а <> 1 (25-18) м —— В от второй Скорость изменения температуры за единицу времени в любой точке относительного тела не зависит от координат и времени. Значение m называется нормальным режимом темпа и определяет
опыт. Взяв точку в теле и измерив температуру этой ячейки, процесс охлаждения можно представить кривой 5 = f (t) (рис. 25-2). Значение m явно равно тангенсу угла прямой волны по отношению к абсциссе. m = (in-lnft2) / (x2-tt). (25-19) Разработанная М. Кондратьевым теория регулярных режимов теплопроводности может быть применена к
объектам любой формы. Это позволило установить связь между скоростью регулярного режима, его физическими геометрическими величинами и внешними условиями теплообмена. В общем случае величина m определяется из уравнения 1. ‘m = -i-e’ (25-20) S (25-16) Рисунок 25-2 Логарифм последнего уравнения, In ft = In (AU) -rm = -mi -f + C (xty, z). (25-17) кн. Величина m, которая характеризует скорость охлаждения тела, прямо пропорциональна коэффициенту
теплопередачи a поверхности F тела (если a не oo) и обратно пропорциональна его неравномерности температуры тела & = cpU, ij) -неоднородности температуры тела Безразмерная пропорциональность, которая характеризует уникальное распределение, является функцией биологического числа. Это уравнение представляет закон сохранения энергии охлаждающей среды в среде с постоянной температурой. Когда ty = 1, распределение температуры в теле равномерно. Для ty-0 распределение температуры
- наиболее неравномерно — температура поверхности равна температуре среды, а внутренняя температура — это все; Если коэффициент теплопередачи равен a0, величина m прямо пропорциональна: пропорциональна температуропроводности охлаждающего тела: м ^ = а! К или А = КТЖУ (25-21) Где / (Коэффициент пропорциональности зависит от геометрических размеров и формы тела, м2. Например, в случае шара. К = (г / л) 2 Для цилиндра Где r —
радиус / Длина цилиндра. G основана на теории регулярного режима теплопроводности. М. Кондратьев разработал метод определения твердых и жидких теплофизических величин a, Я и c. Эти методы широко используются в технике. Преимущество метода Кондрачева в том, что эксперимент прост и результаты достаточно точны. Это уравнение представляет закон сохранения энергии охлаждающей
среды в среде с постоянной температурой. Когда ty = 1, распределение температуры в теле равномерно. — температура поверхности равна температуре среды, а внутренняя температура — это все; Если коэффициент теплопередачи равен a0, величина m прямо пропорциональна: пропорциональна температуропроводности
Для ty-0 распределение температуры наиболее неравномерно Людмила Фирмаль
охлаждающего тела: м ^ = а! К или А = КТЖУ (25-21) Где / (Коэффициент пропорциональности зависит от геометрических размеров и формы тела, м2. Например, в случае шара. К = (г / л) 2 Для цилиндра Где r — радиус / Длина цилиндра. Основываясь на p-теории, Г. М. Кондратьев (нормальный режим теплопроводности) разработал метод определения теплофизических величин a, и, c и твердых тел и жидкостей. Эти методы широко используются в технике. Преимущество метода Кондратьева в том, что эксперимент прост и результаты достаточно точны.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Теплопроводность при нестационарном режиме
Процессы передачи теплоты, в которых температурное поле и поле теплового потока изменяются во времени, называются нестационарными.
Нестационарные тепловые процессы в технике и природе встречаются практически чаще, чем стационарные. Нагрев или охлаждение приборов и машин при пуске, останове или изменении режима; конструктивных элементов зданий и других сооружений при изменении наружной температуры; термическая обработка продуктов и изделий; работа регенеративных теплообменных аппаратов – все это примеры нестационарных тепловых процессов.
Длительность процессов нестационарного конвективного теплообмена и излучения сравнительно мала и не имеет существенного влияния на формирование температурных полей тел в нестационарном режиме, поэтому эти процессы пока мало изучены – их нестационарностью обычно пренебрегают. Процессы же теплопроводности, наоборот, оказывают решающее влияние на формирование температурных полей при нестационарном тепловом состоянии отдельных тел и систем.
Процессы нестационарной теплопроводности можно разделить на две группы: а) нестационарные процессы, связанные с нарушением теплового равновесия, когда с течением времени система стремится к некоторому новому равновесному состоянию; б) нестационарные процессы, связанные с периодическим изменением теплового состояния тела (периодические изменения температуры окружающей среды или мощности тепловых источников и т. п.).
В большинстве задач нестационарной теплопроводности требуется найти температуры в определенных точках тела в заданный момент времени t от начала процесса. Возможна и обратная задача: найти длительность процесса, в результате которого температура в данной точке тела примет определенное, наперед заданное значение. В некоторых задачах бывает необходимо найти тепловой поток в определенной точке в заданный момент времени или полное количество теплоты, отданной (или полученной) телом в течение заданного промежутка времени.
Все перечисленные задачи сводятся к нахождению температуры рассматриваемого тела как функции времени и координат t = f(t, x, у, z).
Эту зависимость можно найти, если проинтегрировать дифференциальное уравнение теплопроводности при заданных краевых условиях.
Для некоторых конкретных задач теплопроводности дифференциальное уравнение может быть упрощено: в случае передачи теплоты в одном направлении задача становится одномерной; при распространении теплоты в двух направлениях задача является двухмерной. Для тел цилиндрической формы удобно перейти к цилиндрическим координатам, а для тел шаровой формы – к сферическим.
Дифференциальное уравнение и краевые условия полностью формулируют задачу. Дальнейшее аналитическое ее решение сводится к использованию методов математической физики. Основные из них: метод разделения переменных, методы интегральных преобразований (например, Лапласа), метод мгновенных точечных источников. Кроме аналитических применяют и приближенные методы.
В качестве примера рассмотрим охлаждение неограниченной пластины.
Охлаждение неограниченной пластины
Будем рассматривать задачу теплопроводности при постоянных значениях теплофизических характеристик тела (l, с,r) с граничными условиями третьего рода, так как они наиболее часто встречаются на практике. Задача формулируется следующим образом. Плоская неограниченная пластина толщиной d, имеющая во всех точках одинаковую начальную температуру tнч, в момент времени t = 0 помещается в среду, температура которой tж 0. Математически задачу можно сформулировать следующим образом. Дифференциальное уравнение теплопроводности для одномерной задачи без внутренних источников теплоты
,
где х может изменяться в пределах 0 £ х £ d/2: так как охлаждение пластины происходит симметрично, целесообразно поместить начало координат в середину пластины и рассматривать процесс только в одной ее половине (см. рисунок). Краевые условия:
1) начальное условие при t = 0 и 0 £ х £ d/2 t = tнч;
2) граничные условия: а) при х = 0и t > 0 (дt/дx)0 = 0, т. к. при симметричном охлаждении в середине пластины в любой момент времени температура будет максимальной; б) при х = l и t > 0 —l(дt/дx)c = a(tc – tж).
Последнее выражение записано на основании равенства тепловых потоков на поверхности пластины: подходящего к поверхности из внутренних областей тела путем теплопроводности и отводимого от поверхности в процессе теплоотдачи.
Решение задачи в общем виде можно представить как функцию независимых переменных х и t и параметров процесса а,l, a, l, tж, tнч:
Следуя методу подобия, приведем условия задачи к безразмерной форме; это значительно сокращает число переменных, придает полученному решению обобщенность, и упрощает анализ решения.
Для этого произведем сначала замену искомой величины t так называемой избыточной температурой J = t – tж.
Так как dJ = dt,то запись дифференциального уравнения и граничных условий от такой замены не изменится:
;
Приведем уравнение и граничные условия к безразмерному виду. Для этого еще раз произведем замену переменных: вместо избыточной температуры введем безразмерную избыточную температуру Q = J/Jнч.Вместо координаты х введем безразмерную координату Х = х/l.Такая замена равносильна тому, что в качестве масштаба для измерения температуры используется величина Jнч, а в качестве масштаба длины – величина l. Для сохранения равенств исходные уравнения в соответствующих местах необходимо умножить на масштабы температуры и длины. Тогда дифференциальное уравнение будет иметь вид:
, или после сокращения и преобразования 
.
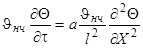
В такой форме дифференциальное уравнение безразмерно: величина l 2 /а имеет размерность времени и потому комплекс аt/l 2 безразмерен. Этот комплекс обозначается символом Fo и называется критерием Фурье:
Критерий Фурье можно трактовать как безразмерное время.
Окончательно дифференциальное уравнение теплопроводности в безразмерной записи получается в следующем виде:
.
Начальное условие: при Fo = 0, Qнч = 1;
где Qс = Jс/Jнч – безразмерная температура поверхности стенки; Bi = al/l – критерий Био.
Физический смысл критерия Био в том, что его величина характеризует соотношение интенсивностей отвода теплоты в процессе теплоотдачи и подвода теплоты из внутренних слоев тела к поверхности в результате теплопроводности.
Теперь искомая функция будет иметь вид Q = f(Fo,Bi, X).
Применяя метод разделения переменных решение дифференциального уравнения будет иметь вид
, (1)
где 
– коэффициенты уравнения;
mп – корни характеристического уравнения m/Bi = ctgm.
Значения mп и Ап приводятся в справочниках.
Результирующее выражение температурной функции, в форме произведения функции времени exp(-m 2 Fo) на некоторую функцию от координаты справедливо не только для пластины, но и для других тел, в которых распространение теплоты происходит в одном направлении, как, например, в бесконечно длинном цилиндре или шаре. Различаются результирующие выражения видом функции координаты: вместо cos – для пластины, для цилиндра появляется функция Бесселя, а для шара – гиперболическая. Для классических тел получены аналитические решения задач нестационарной теплопроводности.
В соответствии с формой результирующих уравнений (1) порядок решения задачи нестационарной теплопроводности для тела классической формы следующий:
1. На основании исходных данных вычисляют безразмерную координату Х и критерии Bi и Fo. Здесь характерный размер тела: для пластины при симметричном охлаждении l = d/2,при одностороннем охлаждении l = d;для бесконечно длинного цилиндра и шара l = R,где R – радиус.
2. По величине критерия Bi в специальных таблицах находят значения mn и Ап для нескольких значений п.В обычных инженерных расчетах достаточно учитывать два-четыре члена суммы в формуле (1).
3. По формуле (1) или аналогичной ей для тел другой формы вычисляют значение безразмерной температуры Q в данной точке в заданный момент времени. Из Q определяют искомую температуру t = f(t, x).
Анализ решения (1) позволяет выявить влияние величины числа Bi на нестационарную теплопроводность. Рассмотрим два предельных случая: Bi ® ¥ и Bi ® 0.
Первый предельный случай:Bi ® ¥ (практически Bi >100). Для тела конечных размеров (l – конкретная конечная величина) этот случай соответствует условию a/l ® ¥, т. е. большим значениям коэффициента теплоотдачи a и сравнительно малым значениям коэффициента теплопроводности l.В этом случае сразу после начала процесса температура поверхности тела принимает и в дальнейшем сохраняет постоянное значение tc = tж = const. Следовательно, интенсивность процесса охлаждения (нагрева) определяется внутренним процессом теплопроводности в теле и зависит только от физических свойств и размеров тела.
При этом общее решение (1) упрощается: из числа определяющих критериев выпадает критерий Bi. Так, для точек, расположенных в средней плоскости пластины (при Х = 0), уравнение для безразмерной температуры при Fo > 0,3 приобретает вид
.
Второй предельный случай:Bi ® 0 (практически при Bi 2 ; Biпл = al/l; Foпл = аt/l 2 .
Величины Qц иQпл могут быть найдены по графикам с учетом расположения рассматриваемой точки в безграничном теле. Так, для точки 1 (рис.)величина Qц находится по графику для центральных точек неограниченного цилиндра, а величина Qпл – по графику для средней плоскости пластины. Для точки 2величина Qц определяется по тому же графику, что и для точки 1, а Qпл – по графику для поверхностных точек пластины. Для точки 3обе величины находятся по графикам для поверхностных точек цилиндра и пластины. Для точки 4величина Qц определяется по графику для поверхностных точек цилиндра, а величина Qпл – по графику для средней плоскости пластины. Перечисленные четыре точки являются характерными для ограниченного цилиндра. Температуры остальных точек ограниченного цилиндра по графикам не могут быть найдены, но для их определения можно воспользоваться соответствующими формулами.
Аналогичные рассуждения справедливы и для параллелепипеда,но его следует рассматривать как тело, образованное пересечением трех неограниченных пластин.
Регулярный режим охлаждения (нагревания) тел
При значении Fo > 0,3 в выражениях типа (1) достаточно ограничиться одним первым членом ряда. В этом случае для пластины
. (2)
Режим охлаждения (или нагрева), определяемый формулой (2), называется регулярным. Этот результат обобщается и на более сложные задачи охлаждения (нагрева) тел любой геометрической формы при условии tж и a = const:
,
где m – темп охлаждения, [1/с].
В этом случае начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела, его геометрической формой и размерами.
Логарифмируя последнее уравнение, получаем:
Из последнего уравнения следует, что натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линейному закону. Если продифференцировать это выражение по времени получим:
.
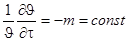
В левой части уравнения стоит выражение для относительной скорости изменения температуры, и оно равняется постоянному значению т,не зависящему ни от координат, ни от времени. Следовательно, темп охлаждения характеризует относительную скорость изменения температуры в теле и зависит только от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.
Если экспериментально определить изменение избыточной температуры Jво времени t и построить зависимость в полулогарифмических координатах, то темп охлаждения в стадии регулярного режима найдется как
.
Выражение для зависимости темпа охлаждения т от физических свойств тела, его геометрической формы и размеров, а также условий теплообмена на поверхности тела можно найти из анализа теплового баланса. В результате получим:
,
где С – полная теплоемкость тела;
y = JF/JV – коэффициент неравномерности распределения температуры в теле;
JF, JV – средние по поверхности и по объему температуры тела.
Из уравнения следует, что темп охлаждения т, однородного тела при конечном значении коэффициента теплоотдачи a пропорционален коэффициенту теплоотдачи, поверхности тела и обратно пропорционален его теплоемкости (первая теорема Кондратьева ).
Коэффициент y зависит от числа Bi, учитывающего условия протекания процесса на поверхности тела. Рассмотрим два предельных случая:
а) Bi ® 0 (практически Bi 100). При этом условии задача становится внутренней, и процесс охлаждения определяется только размерами тела и его физическими свойствами. В силу большой интенсивности теплообмена температура на поверхности тела принимает постоянное значение, равное температуре окружающей среды. Коэффициент неравномерности распределения температуры y = 0.
При Bi ® ¥, или, что то же, a ® ¥, темп охлаждения т становится прямо пропорциональным коэффициенту температуропроводности тела а (вторая теорема Кондратьева):
.
Коэффициент пропорциональности К зависит от геометрической формы и размеров тела и определяется в зависимости от формы тела по выражениям:
для шара радиусом r 
;
для параллелепипеда с длиной граней l1, l2, l3 
;
для цилиндра длиной l и радиусом r 
.
На основе теории регулярного режима разработаны различные экспериментальные методики определения теплофизических характеристик материалов.
Основы теории теплообмена
Теория теплообмена, основные понятия и определения. Теплопроводность. Предмет и методы теории теплообмена. Основные виды переноса теплоты. Понятия теплоотдачи и теплопередачи. Температурное поле, температурный градиент. Закон Фурье. Расчетные формулы стационарной теплопроводности для плоской и цилиндрической стенок при граничных условиях 1 и 3 рода (теплопередача).
Основы теории теплообмена
Теплопередача — это процесс переноса теплоты от одного теплоносителя к другому через разделяющую стенку. Теплопередача связана с весьма сложными процессами и при ее изучении необходимо знать законы теории теплообмена и методы анализа, применяемые в физике, термодинамике, гидродинамике и химии.
Сложный процесс переноса теплоты разбивают на ряд более простых. Такой прием упрощает его изучение. Кроме того, каждый простой процесс переноса теплоты подчиняется своим законам. Существует три простейших способа передачи теплоты: теплопроводность, конвекция, излучение.
Явление теплопроводности состоит в переносе теплоты микрочастицами (молекулами, атомами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур.
Конвективный теплоперенос (конвекция) наблюдается лишь в жидкостях и газах. Конвекция — это перенос теплоты вместе с макроскопическими объемами вещества. Следует иметь в виду, что одновременно с конвекцией всегда существует и теплопроводность. Однако конвекция обычно является определяющей, т. к. она интенсивнее теплопроводности.
Конвекцией можно передавать теплоту на очень большие расстояния (например, при движении газа по трубам). Движущаяся среда (жидкость или газ), используемая для переноса теплоты, называется теплоносителем.
Третьим способом переноса теплоты является излучение. За счет излучения теплота передается во всех лучепрозрачных средах, в том числе и в вакууме. Носителями энергии при теплообмене излучением являются фотоны, излучаемые и поглощаемые телами, участвующими в теплообмене.
В большинстве случаев перенос тепла осуществляется несколькими способами одновременно. Например, конвективная теплопередача от газа к стенке практически всегда сопровождается параллельным переносом теплоты излучением.
Основные понятия и определения
Интенсивность переноса теплоты характеризуется плотностью теплового потока. Плотность теплового потока — это количество теплоты, передаваемое в единицу времени через единичную плотность поверхности, q [Вт/м2].
Мощность теплового потока или просто тепловой поток — это количество теплоты, передаваемое в единицу времени через произвольную поверхность F, [Вт].
поверхность теплообмена F — это поверхность, через которую происходит передача тепла. Например, при остывании теплоносителя в трубе диаметром d и длиной l, тепло передается от горячего теплоносителя к окружающей среде через цилиндрическую поверхность трубы. В этом случае 
.
Перенос теплоты зависит от распределения температуры по объему тела или пространства. Температурным полем называется совокупность мгновенных значений температуры во всех точках тела или системы тел в данный момент времени. Математическое описание температурного поля имеет вид:
где t — температура;
x, y,z — пространственные координаты;
— время.
Температурное поле, описываемое приведенным уравнением, называется нестационарным. В этом случае температуры зависят от времени.
В том случае, когда распределение температуры в теле не изменяется со временем, температурное поле называется стационарным
если температура изменяется только по одной или двум пространственным координатам, то температурное поле называется соответственно одно— и двухмерным:
Температурные поля (1.2) и (1.3) называются трехмерными.
Поверхность, во всех точках которой температура одинакова, называется изотермической. Изотермические поверхности могут быть замкнутыми, но не могут пересекаться. Быстрее всего температура изменяется при движении в направлении, перпендикулярном изотермической поверхности. Скорость изменения температуры по нормали к изотермической поверхности характеризуется градиентом температуры.
Градиент температуры
(grad t) — есть вектор, направленный по нормали к изотермической поверхности и численно равный производной пот температуры по этому направлению:
,
Рисунок 1 — Расположение градиента температуры и вектора теплового потока относительно изотермы t2=Const температурного поля
где 
— единичный вектор, направленный в сторону возрастания температур нормально к изотермической поверхности.
Теория теплопроводности рассматривает тело как непрерывную среду. Согласно основному закону теплопроводности — закону Фурье — вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален вектору градиента температуры:
,
где 
— коэффициент теплопроводности, Вт/(м×К). Он характеризует способность вещества, из которого состоит рассматриваемое тело, проводить теплоту.
Знак «-» указывает на противоположное направление вектора теплового потока и вектора градиента температуры. Вектор плотности теплового потока q всегда направлен в сторону наибольшего уменьшения температуры.
скалярная величина вектора плотности теплового потока:
,
Из формулы следует, что коэффициент теплопроводности 
определяет плотность теплового потока при градиенте температуры 1 К/м.
Коэффициент теплопроводности является физическим параметром и зависит от химической природы вещества и его физического состояния (плотности, влажности, давления, температуры). Диапазоны изменения для различных материалов приведены на рисунке 2.
 |
Рисунок 2 — Теплопроводность при стационарном режиме
Однослойная плоская стенка
Рассмотрим однородную плоскую стенку толщиной d, на поверхностях которой поддерживаются температуры tс1 и tс2, причем tс1>tс2 (рис.3). температура изменяется только по толщине стенки — по одной координате х, коэффициент теплопроводности 
. Теплового потока в этом случае, в соответствии с законом Фурье, определяется по формуле:
,
Рисунок 3 — Изменение температур по толщине однородной плоской стенки
,
где 
, причем tс1>tс2;
— внутреннее термическое сопротивление теплопроводности стенки, (м2×К)/Вт.
Распределение температур в плоской однородной стенке — линейное.
В большинстве практических задач приближенно предполагается, что коэффициент теплопроводности не зависит от температуры и одинаков по всей толщине стенки. значение находят в справочниках при средней температуре 
.
Тепловой поток (мощность теплового потока) определяется по формуле:
,
Многослойная плоская стенка
Рассмотрим для тех же условий многослойную плоскую стенку с толщиной слоев d1, d2,…, dn с соответствующими коэффициентами теплопроводности l1, l2,…, ln (рисунок 4). Здесь слои плотно прилегают друг к другу.
В этом случае плотность теплового потока определяется по формуле:
Рисунок 4 — Распределение температур по толщине многослойной плоской стенки
,
где n — число слоев многослойной стенки;
tc1 и tc(n+1) — температуры на внешних границах многослойной стенки;
— полное термическое сопротивление многослойной плоской стенки.
Плотность теплового потока, проходящего через все слои, в стационарном режиме одинакова. А так как коэффициент теплопроводности l различен, то для плоской многослойной стенки распределение температур — ломаная линия.
Рассчитав тепловой поток через многослойную стенку, можно найти температуру на границе любого слоя. Для к-го слоя можно записать:
,
Однородная цилиндрическая стенка
Задача о распространении тепла в цилиндрической стенке также одномерная, если ее рассматривать в цилиндрических координатах. температура изменяется только вдоль радиуса r, а по длине и по ее периметру остается неизменной.
В соответствии с законом Фурье, тепловой поток через однородную цилиндрическую стенку длиной l определяется по формуле:
,
Тепловой поток Q через цилиндрическую стенку можно отнести к единице длины l:
,
где ql — линейная плотность теплового потока, Вт/м;
— линейное термическое сопротивление теплопроводности трубы.
 |