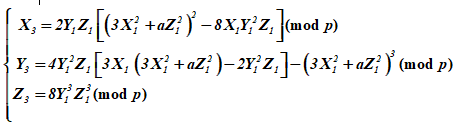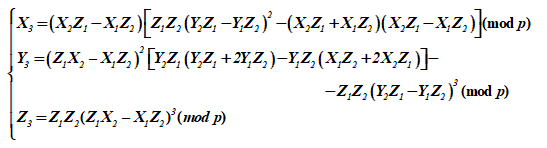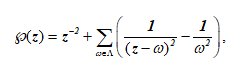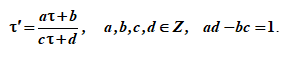Уравнения к плоскости аффинное пространство

Факторизация и эллиптическая кривая. Часть V

К тем сведениям об эллиптических кривых (ЭК), которые доступны читателям Хабра и Интернета в целом, а также из бумажных книг, предлагаю дополнительные, уточняющие важные детали, опущенные в некоторых статьях. Например, в работе приводится изображение тора (рис. 4), но никаких оговорок не делается. Откуда он взялся, почему тор? Другие авторы вообще не упоминают эту фигуру. В чем здесь дело?

Не могу назвать публикацию на Хабре и других сайтах, где автор говорил бы о полях многочленов, хотя обозначение ) таких полей некоторыми авторами и используются, но делается это неправильно. Неприводимый многочлен и примитивный элемент поля и не задаются, что не позволяет читателю построить такое поле и работать с ним, проверить вычислением приводимый результат, если числовой пример вообще приводится. От таких публикаций остается ощущение зря потраченного времени. Такие поля расширения используются в стандартах цифровой подписи и шифрования рядом государств.

Не буду указывать на явные ошибки, читатели в своих комментариях часто сами их указывают, но сделаю попытку высветить общую картину. Попробую перечислить промахи наиболее распространенные и часто повторяемые многими авторами. Практически не называются допущения и ограничения моделей, которые приводятся в публикациях, особенно, когда модель не авторская, а созданная кем-то другим. Важность границ применимости можно не обсуждать — с этим согласны все, но указывается на это авторами исключительно редко.

Пространства изучения моделей

Здесь будем использовать в зависимости от рассматриваемой ситуации различные пространства вещественные и комплексные, аффинные и проективные, бесконечные и конечные подходящей размерности. Поэтому вначале кратко рассмотрим их сущность основные свойства, способы описания. Для практики фактически наибольший интерес представляет конечный случай.

Аффинные пространства

Рассмотрим множество наборов (а1, а2, …, аn) из n элементов, где каждый аi ∊ F и F некоторое поле. Множество наборов обозначим символом и обычным способом введем для наборов операции сложения и умножения на скаляры. При условии замкнутости множества по этим операциям оно образует векторное пространство с аддитивным нейтральным элементом О = (0, 0, …, 0).

Для удобства в дальнейшем условимся обозначать набор (а1, а2, …, аn) символами а, в, с…, а будем называть n-мерным аффинным пространством, его элементы – аффинными точками, точку О = (0, 0, …, 0) – назовем началом координат. Если F — конечное поле из элементов, где р – простое, то содержит элементов (наборов, точек). При р = 2 получаем множество всех двоичных чисел разрядности k.

Аффинная плоскость

Пусть F˟ – конечное алгебраически замкнутое поле и Fо – некоторое подполе поля F˟. Аффинная плоскость под полем F˟ (дискретная конечная F˟×F˟ ) представляет собой множество всех <(α, β)>упорядоченных пар элементов α, β поля F˟. Каждую такую пару Q=(α, β) называют точкой плоскости , а элементы α, β – координатами точки Q. Если поле F˟ является полем расширения некоторой степени n, то каждая координата точки Q представляет собой многочлен степени не выше n – 1 от формальной переменной t.

Эллиптической кривой (ЭК) над полем F называется плоская гладкая кривая с уравнением вида
Индексы у коэффициентов в уравнении указывают степени, которые должны быть приписаны этим коэффициентам, чтобы уравнение ЭК стало однородным, т.е. чтобы каждое слагаемое в нем имело общую степень 6.

Через Е(F) обозначают множество, состоящее из точек , удовлетворяющих этому уравнению, с добавлением «бесконечно удаленной» точки О. Если К — некоторое расширение поля F, то через Е(К) будет обозначаться множество, состоящее из точек удовлетворяющих уравнению ЭК и бесконечно удаленной точки О.

Пример 1. Для поля с характеристикой p = 5 и степенью расширения n = 3 задается примитивный элемент (α) и неприводимый многочлен Порядок поля при этом , а аффинная плоскость содержит точек с многочленами в роли координат точек.

Например, задание одной из точек эллиптической кривой в этом поле имеет вид , где многочлены – координаты точки Q. Малая часть точек такой дискретной плоскости образует ЭК и еще меньшая их часть — является аддитивной группой точек ЭК, которая строится здесь.

Пусть F˟ – алгебраическое замыкание поля поля F. Условие гладкости кривой означает, что в множестве Е(F˟) не существует точек, в которых одновременно обращались бы в нуль частные производные где

Иными словами, система уравнений

не имеет решений, принадлежащих Е(F˟).

Проективное пространство

Символом по аналогии с предыдущим будем обозначать n-мерное проективное пространство над полем F. Очень важно понимать, как устроено это пространство, и в чем отличие от . С этой целью рассмотрим вначале – множество наборов (ао, а1, …, аn), в котором точка O=(0, 0, …, 0) – начало координат удалена.

Над множеством определим отношение эквивалентности: n–мерная точка а = (ао, а1, …, аn) эквивалентна точке b = (bо, b1, …, bn), если существует такой элемент γ∊F*, где F* – мультипликативная группа поля F, что aо=γbо, a1=γb1. an=γbn. Просто убедиться в том, что все такие пары (a, b) из образуют отношение (

) эквивалентности, которое индуцирует разбиение множества – на классы эквивалентности.

Все такие классы называются точками пространства и все элементы класса (т.е. сам класс) обозначаются символом [а], если точка а = (ао, а1, …, аn) входит в состав класса, то такая точка а называется представителем класса. В геометрической терминологии все элементы (точки) произвольного класса [а] принадлежат прямой в пространстве , проходящей через точку а и начало координат в аффинном пространстве.

Пространство образованно элементами (точками). Это легко показать, так как пространство имеет элемент (без нулевого), мультипликативная группа F* поля F˟ состоит из q – 1 элементов (точек проективного пространства). Каждый класс эквивалентности (прямая) порождается произвольным элементом а = (а0, а1, …, аn) умноженным на каждый элемент из F*, т.е. содержит q – 1 элементов.

Тогда число |H˟| классов (их объёмы одинаковы) эквивалентности можно подсчитать по формуле:
Сравнение мощностей n–мерных пространств аффинного и проективного показывает, что | A^n(F) |$» data-tex=»inline»/>.

Пример 2: Пусть . Тогда – мощность (порядок – число элементов) аффинного пространства ;
— мощность (порядок) аффинного пространства ; в нем |H˟| классов. — мощность (порядок) проективного пространства , т.е. число классов эквивалентности точек пространства . Видим, каждый класс эквивалентности содержит 7 элементов. | A^n(F) |$» data-tex=»inline»/>. =>585>512.

Проективная плоскость

Наряду с аффинной плоскостью в криптографии с эллиптическими кривыми используется проективная плоскость. Это связано с тем, что для ЭК, задаваемой в этой плоскости, формулы для групповой операции с точками ЭК не содержат действия деления, т.е. для вычисления координат результирующей точки не требуется обращения элемента в поле F, которая весьма трудоемка. Иногда для проективной плоскости используют обозначение , чтобы подчеркнуть вещественную природу (некомплексную) элементов.

Определение. Приведем в определении тройственное представление проективной плоскости:
= <прямые в , проходящие через начало координат> =
= <отношение вида X: Y: Z>=
= < \<0>/

, где (X: Y: Z), (γХ:γY:γZ), если γ∈R\0>.

В нижней (последней) строчке определения записано фактормножество точек пространства (трехмерного, вещественного) по отношению эквивалентности (

), где γ принадлежит F* -множеству вещественных чисел без нуля, т.е. мультипликативной группе поля.

Рисунок 1 – Аффинная плоскость Z = 1

Легко может быть выполнен переход к произвольному векторному пространству над любым полем. Для того, чтобы представить отношение X: Y: Z для Z = 0, достаточно положить x = X/Z,
y = Y/Z. Этим достигается упрощение, так как исходное отношение задается теперь парой вещественных чисел.

Другими словами, класс эквивалентности троек (x, y, z) по отношению эквивалентности имеет единственного представителя (x, y, 1), третья координата которого Z /Z = 1 для всех точек.
К сожалению, Z все-таки может обращаться в нуль, и в этом случае наш способ представителя класса эквивалентности не годится.

Приведенное рассуждение показывает, что содержит экземпляр пространства

Рисунок 2 – Замены переменных, переводящие кривую в проективное пространство

Прямая общего положения в , проходящая через О, не содержится в плоскости (Z = 0) и, значит пересекает плоскость (Z = 1) в единственной точке, которая и представляет собой этот класс эквивалентности (т.е. прямую L в ). Прямые, лежащие в плоскости (Z = 0), не пересекают плоскость (Z = 1). Следовательно, они соответствуют не точкам из а асимптотическим направлениям или пучкам параллельных прямых в . Таким образом, можно представить как пространство, состоящее из плоскости , к которой добавлено по одной “точке на бесконечности” для каждого пучка параллельных прямых.

Ньютон занимался и кубическими кривыми, привел их классификацию, им сформулирована Теорема. Для любой неособой кубической кривой существует проективная замена координат, преобразующая кубическую кривую к кривой в форме Вейерштрасса с рациональными а и b. Например, m(m+1)/2=n(n+1)(2n+1)/6 после замены m=(у-9)/18 и n=(x-3)/6 получаем уравнение рациональные корни которого и будут решением задачи.

Приведем кривую к форме Вейерштрасса. Выполним проективную замену координат х = s -t, y = t. Эта замена осуществляет параллельную проекцию плоскости ху на плоскость st. Получаем кривую. Теперь спроецируем плоскость st на плоскость uv из центра. Еще одна замена координат s=1/3u и t =(6v+1)/6u. Новая кривая (в форме Вейерштрасса) получает вид

Вопрос на понимание ЭК: Какие два натуральных смежных числа при умножении у(у+1) равны произведению трех натуральных смежных чисел (х-1)х(х+1)? В уравнении есть как в ЭК.

Формулы групповой операции ЭК в проективном пространстве (плоскости).
Пусть задано уравнение ЭК в проективной плоскости в форме Вейерштрасса Е(GF(q)):

над полем характеристики р, (р ≠ 2 и р ≠ 3), получаемое путем перевода ЭК из аффинной в проективную плоскость. Точки такой ЭК можно рассматривать как эквивалентный класс точек (X, Y, Z) плоскости над полем GF(q).

Бесконечно удаленная точка O ,O ∈ представляет все ненулевые точки с отношением эквивалентности (X, Y, Z)

(kX, kY, kZ). Такие точки обозначаются как (X, Y, Z) и среди них имеется единственная точка с координатой Z = 0 – это точка (0, 1, 0). При Z = 0 обязательно и Х = 0, и существует только один класс эквивалентности с Х = Z = 0, содержащий бесконечно удаленную точку (0, 1, 0)∈ Е(GF(q))∈ .

Существует возможность и обратного перевода ЭК из пространства в аффинное пространство . Для всех точек Q = (X, Y, Z) ≠ O производится замена (X, Y, Z) = (Х/Z, Y/Z, 1). При этом выполняется однозначное соответствие: точке (х = Х/Z, y = Y/Z) соответствует точка (X, Y, Z).
Формулы удвоения точки ЭК в проективном пространстве принимают вид:

,
где координата кратна λ.

Последующие преобразования обеспечивают получение формул группового сложения точек ЭК в проективных координатах.

Суммирование пары различных точек группы ЭК в проективном пространстве соответствует некоторой третьей точке этой группы, имеющей три координаты. Так третьей координатой является , а весь набор получает вид

При рассмотрении ЭК над расширенным полем , имеющих инвариант j ≠ 0 формулы принимают иной вид для случая

Комплексное пространство C

Эллиптическую кривую можно рассматривать не только в аффинном, проективном, но и в комплексном пространствах. В последнем случае точки ЭК называются комплексными точками. Далее будем рассматривать именно такие точки над комплексными полями.

Поскольку ЭК – это плоская кривая, то ограничимся рассмотрением комплексной проективной плоскости . В этой плоскости можно задавать функции, которые имеют два линейных независимых периода. Их называют мероморфные двоякопериодические функции с периодами ω1, ω2.

По причине линейной независимости периодов над R, ω1/ω2∈R. Другое название для таких функций – эллиптические функции. Для наших целей интерес представляет функция Вейерштрасса ℘(z), которая удовлетворяет дифференциальному уравнению вида

где – некоторые константы, зависящие от периодов ω1, ω2.

Сходство записанного уравнения с ЭК весьма значительное.
Зададим на плоскости С решетку Λ= периодов, где m и n — целые числа и узлы решетки Λ целочисленные. Элементы решетки образуют нормальную подгруппу в группе комплексных чисел, и мы можем сформировать по этой группе факторгруппу C/Λ.

Позднее покажем, что элементы факторгруппы можно отобразить в комплексные точки Е(С) ЭК Е, и такое отображение взаимно однозначно.
Многочлен правой части ЭК над комплексной плоскостью С.
Параметризацию удаётся осуществить для части ЭК на С, благодаря выбору необходимой функции ℘.

В проективной комплексной плоскости с учетом полюсов функции ℘ параметризация устанавливает взаимно однозначное соответствие между множеством точек C/Λ и множеством Е(С) комплексных точек кривой Е. Такое соответствие оказывается биголоморфно.

Суммирование комплексных чисел определяется групповым законом сложения на торе C/Λ. Ниже будет показано, что соответствие φ: C/Λ→Е(С) ЭК Е. Далее выясняется, что любая ЭК на С может быть нормализована подбором подходящей функции Вейерштрасса ℘. В основе процедуры прояснение такой связи лежит возможность обращения эллиптических интегралов.

Эллиптические функции

Определение. Алгебраическую кривую называют эллиптической, если она как одномерное комплексное многообразие представляет собой тор (бублик).
Определение. Мероморфная двоякопериодическая функция называется эллиптической.

Определение. Аналитическая функция называется мероморфной, если у нее в конечной области С нет особых точек, отличных от полюсов.
Определение. Функция:f^C →С∪( <∞>называется двоякопериодической с периодами ω1, ω2 при линейной независимости периодов над R и f(z+ω1)=f(z)=f(z+ω2) для любых z∈C.

Двоякопериодическую функцию называют эллиптической, если она мероморфна. Множество эллиптических функций образует поле при фиксированных периодах ω1, ω2. В плоскости С точки 0, ω1, ω2 и ω1+ω2 образуют вершины параллелограмма
П=<α1ω1+α2ω2|0 ≤α1,α2 ≤1>, который называется фундаментальным. Стороны, сходящиеся в точке 0 и сама точка принадлежат П, а три другие вершины и две стороны — не принадлежат П.

Особый интерес представляет фундаментальный параллелограмм и его граница.
Определение. Фундаментальным параллелограммом называется область плоскости С, заданная соотношением П = <α1ω1+α2ω2|0 ≤α1,α2 ≤1>где α1,α2∈R.
Параллелограммом периодов называется любой параллелограмм вида α+П, α∈С. Для всех таких параллелограммов справедливы одинаковые условия.

Относительно эллиптических функций Ж. Лиувиллем (1809-1882) сформулированы и доказаны следующие результаты.

Теорема 1. Не существует отличных от констант целых эллиптических функций.
Доказательство. Целая эллиптическая функция непрерывна, так как не имеет полюсов; поэтому она ограничена на замыкании П. В силу периодичности функция ограничена на С, следовательно, она постоянна.

Следствие 2. Две эллиптические функции, имеющие одинаковые наборы полюсов и соответственно равные главные части в полюсах, отличаются на константу.

Теорема 3. Если эллиптическая функция f(z) не имеет полюсов на границе L параллелограмма П+α, то сумма вычетов f(z) во всех полюсах, лежащих внутри П+α, равна 0.

Эллиптическая функция Вейерштрасса. Эта функция играет важную роль для всей теории эллиптических функций в силу ее замечательных свойств. Займемся рассмотрением этих свойств подробнее и выясним, как и какие из них могут быть использованы для наших целей, связанных с изучением ЭК. Функция Вейерштрасса определяется над комплексной плоскостью C и представляется формулой.

,
где Λ не содержит точку 0, т.е. решетка периодов с удаленной точкой 0 и фиксированными значениями ω1, ω2. Выражение под знаком суммы нельзя записывать через две суммы, так как каждая из них представляет расходящийся ряд.

Комплексная плоскость C с решеткой Λ

Перейдем к рассмотрению комплексного случая ЭК.
Пусть ω1 и ω2 — два линейно независимых на R комплексных числа. Обозначим через
Λ= порожденную ими решетку. Отождествим две точки комплексной плоскости С, если их разность принадлежит Λ. После такого отождествления получим фактор-пространство С/Λ.

На рисунке заштрихованная часть комплексной плоскости представляет собой фундаментальную область – параллелограмм, сдвиги которого на элементы из Λ накрывают всю плоскость С.

Рисунок 3. Фундаментальный параллелограмм в комплексной плоскости

Фактор-пространство С/Λ можно представить в виде фундаментального параллелограмма с отождествленными противоположными сторонами. Так как сложение комплексных чисел (x,y) → x+y задает некоторое голоморфное отображение C×C→C, то С является комплексной группой Ли, а Λ – ее подгруппой. Таким образом, фактор-пространство С/Λ – компактная комплексная группа Ли.

Пару (ω1, ω2) можно умножить на комплексное число или и получить пару, состоящую из 1 и τ, где Imτ>0. Соответствующую решетку, порожденную 1 и τ обозначим через Λτ, а фактор-пространство С/Λτ через Eτ. Каждое пространство С/Λ изоморфно одному из Eτ, причем Eτ и E’τ изоморфны тогда и только тогда, когда

Функции на С/Λ. Пусть g – мероморфная функция на С/Λ. Тогда q∙g – мероморфная функция на С, удовлетворяющая условиям q·g(z+ω1) = q·g(z+ω2) = q·g(z)
Таким образом, q∙g – двоякопериодическая мероморфная функция на С. Обратно, каждая двоякопериодическая мероморфная функция на С (так называемая эллиптическая функция) определяет некоторую мероморфную функцию на С/Λ.

Основная эллиптическая функция может быть представлена в виде ряда:

Рисунок 4 – Представление ЭК в области фундаментального параллелограмма тороидальной поверхностью

На рис. 4 изображен тор, слева развертка его поверхности (плоский лист-прямоугольник). Развертка получена двумя перпендикулярными разрезами тора: вертикальным (в сечении дает малую окружность — торцы цилиндрической поверхности) и горизонтальным вдоль образующей цилиндра, получаемого после первого разреза, и распрямления (топология) вдоль осевой линии. Линии разрезов: первая совмещается с координатной осью ординат (у), вторая — границы (верхний и нижний края развертки) равноудаленные от оси абсцисс (х). Все целочисленные точки группы ЭК в этой системе координат получают вид (х, у).

Действительно, на рисунке видим симметричное относительно оси х расположение точек. Сплошная линия на торе (синяя) без разрывов на развертке представлена 4-я отрезками, концевые точки которых соответственно имеют совпадающие координаты. Другими словами, обратными действиями (склейкой) можно получить объемную фигуру — тор, на поверхности которого все отрезки прямых воссоединятся в замкнутую пространственную винтовую линию. Условность этой иллюстрации в том, что плоская ЭК представляется в комплексной плоскости двоякопериодической функцией, удовлетворяющей уравнению Вейерштрасса.

Эта функция мероморфна на С, двоякопериодическая и имеет полюсы кратности 2 в точности в вершинах решетки Λ. Очевидно, что и производная ℘’(z) является двоякопериодической функцией, имеющей полюсы кратности 3 в вершинах решетки Λ.
℘(z) и ℘′(z) связаны между собой некоторым полиномиальным соотношением:
f(℘(z), ℘′(z), 1) = 0.

Факторизация из полезных возможностей ЭК

— разложение составного числа N на множители.
Формально алгоритм, предложенный Ленстрой содержит следующие шаги.
ш1. Выбирается ЭК над полем порядка N, т.е. целые числа из диапазона .
ш2. Рассматриваем кубическую кривую и базисную точку ЭК .

ш3. Вычисляем ; этим проверяется являются ли редукции кривой Е эллиптическими. Если НОД =N, переход к Ш1 и выбор нового b. Если , то получен нетривиальный делитель числа N. При , переход к Ш4

ш4. Выбираем число k, являющееся произведением небольших простых чисел в небольших степенях: k=НОК(2,3, . М), где М-натуральное число.
ш5. Вычисляем кратную базисной точку
ш6. Вычисляем . Если 1 Список использованной литературы

47. Аффинная система координат на прямой, плоскости и в пространстве

В случае прямой базис состоит из одного ненулевого вектора V = (V) и система координат (О, V) изображена на рис. 4.1. В системе координат на прямой каждая точка A прямой имеет одну координату A(X), определяему разложением вектора По базису, = XV. Тогда A(0), E(1), где V = .

Систему координат на прямой можно задать еще следующими способами:

Двумя различными точками О и E данной прямой. Тогда одну из точек, например О, берем в качестве начала системы координат, а в качестве базисного вектора возьмем вектор V = (см. рис. 4.2).

Точкой О, единичным отрезком ОE и положительным направлением данной прямой, которое отмечается стрелкой.

2Аффинная система координат на плоскости. В случае плоскости базис состоит из двух неколлинеарных векторов плоскости, V = (V1, V2), и система координат (О, V1, V2) изображена на рис. 4.3. В системе координат на плоскости каждая точка A плоскости имеет две координаты A(X, Y), определяемые разложением вектора По базису, = XV1+ YV2. Тогда A(0, 0), E1(1, 0), E2(0, 1), где V1 = , V2 = . Координаты точки называются соответственно Абсциссой и Ординатой.

Систему координат на плоскости можно задать еще следующими способами:

Тремя точками О, E1, E2 плоскости, не лежащими на одной прямой. Тогда одну из точек, например О, берем в качестве начала системы координат, а в качестве базисного вектора возьмем векторы V1 = , V2 = .

Двумя пересекающимися числовыми осями ОX, ОY данной плоскости с общим началом О. Ось ОX называется Осью абсцисс, ось ОY — Осью ординат.

Аффинная система координат (О, V1, V2) называется Правой (Левой), если поворот от вектора к вектору по кратчайшему направлению совершается против часовой стрелки (по часовой стрелке). На рис. 4.3 и 4.4 представлены правые системы координат.

3. Аффинная система координат в пространстве. В случае пространства базис состоит из двух некомпланарных векторов пространства, V = (V1,V2, V3), и система координат (О, V1, V2, V3) изображена на рис. 4.5. В этой системе координат каждая точка A пространства имеет три координаты A(X,Y,Z), определяемые разложением вектора по базису, = XV1+ YV2 + ZV3. Тогда A(0, 0, 0), E1(1, 0, 0), E2(0, 1, 0), E3(0, 0, 1), где V1 = , V2 = , V3 = . Координаты точки называются соответственно Абсциссой, ординатой и Аппликатой.

Истему координат в пространстве можно задать еще следующими способами:

Четверкой точек О, E1, E2, E3 пространства, не лежащими на одной плоскости. Тогда одну из точек, например О, берем в качестве начала системы координат, а в качестве базисного вектора возьмем векторы V1 = , V2 = , V3 = .

Тремя числовыми осями ОX, ОY, ОZ, не лежащими в одной плоскости с общим началом О. Ось ОX называется Осью абсцисс, ось ОY — Осью ординат, ось ОZ — Осью аппликат.

Аффинная система координат (О, V1, V2, V3) называется Правой (Левой), если тройка векторов V1, V2, V3 правая (левая) На рис. 4.5 и 4.6 представлены правые системы координат, а на рис. 4.7 левая система координат.

1 Аффинное пространство

Считается, что классическая механика (КМН) в объеме трех законов Ньютона с определением ИСО определяется в евклидовом пространстве. Но это не совсем так. Классическая механика (КМН) в объеме трех законов Ньютона определена в аффинном пространстве. Это видно из того, что во всех трех законах Ньютона не присутствуют понятия о расстояниях и углах. Есть понятия только о прямых и векторах. И, конечно, понятие параллельности. Действительно, любые линейные преобразования координат не меняют основные законы Ньютона.

1. 1-й закон. При аффинных преобразованиях координат ИСО остается ИСО, прямые переходят в прямые, вектора – в вектора. Косоугольность (понятие евклидова пространства) с.к. не имеет значения, потому как с.к. ИСО может быть и косоугольным.

2. 2-й закон. При аффинных преобразованиях координат векторы остаются векторами и преобразуются по своим законам. Нулевой вектор при этом остается нулевым.

3. 3-й закон. Линия действия двух взаимодействующих тел и равенство сил взаимодействия не меняется при аффинном преобразовании координат.

4. В аффинном пространстве остаются в силе законы сохранения импульса и массы.

Законы сохранения энергии и момента импульса являются уже законами изотропного метрического галилеева пространства и не следуют непосредственно из трех законов Ньютона.

При введении в рассмотрение криволинейных и неинерциальных систем отсчета (НСО) МН определяется в локально аффинном пространстве. Отношение локально аффинного пространства к аффинному пространству такое же, как риманова пространства к евклидовому пространству.

И только там, где явно появляются расстояние (скалярное приозведение, длина, площадь, объем) и угол, появляются евклидово и риманово пространства. Вместе с ними появляется энергия, моменты векторных параметров и, собственно, классическая механика Ньютона в привычном для нас виде с законами сохранения импульса, энергии и момента импульса.

Итак, что такое аффинное пространство?

1.1 Определение

Аффинное пространство называется действительным или комплексным, конечномерным или бесконечномерным в зависимости от того, каким является соответствующее линейное пространство.

Размерность аффинного пространства равна по определению размерности соответствующего пространства свободных векторов. При этом число точек n в максимальном аффинно независимом множестве точек аффинного пространства оказывается на единицу больше размерности пространства: n = N +1.

Пример: прямая, плоскость и пространство являются аффинными пространствами над векторными пространствами V , V , V .

Аксиомы Вейля аффинного пространства

Пусть A ≠ Ø — множество элементов произвольной природы, называемых точками и обозначаемых A, B, C, . Наряду с этим множеством рассмотрим векторное пространство V.

Определение . Множество A ≠ Ø называется аффинным пространством над векторным пространством V , если задано отображение, сопоставляющее любой упорядоченной паре точек из A некоторый (единственный!) вектор из V :

и удовлетворяющее двум аксиомам (аксиомам Вейля):

Для любой точки A ∈ A и любого вектора v ∈ V существует единственная точка B ∈ A , для которой:

(в дальнейшем будем обозначать v (A, B) = AB).

Данная аксиома связывает с каждой точкой пространства A (называемых точками аффинного пространства) некоторое векторное пространство V (которое называют пространством свободных векторов для аффинного пространства A ).

Разновидностью этой аксиомы является другая – обратная к ней:

Для любых точек A, B ∈ A существует единственный вектор v ∈ V , для которой:

Данная аксиома исключает цикличность координат аффинного пространства. Но пространства с циклическими координатами существуют – их назовем циклическими аффинными пространствами.

Для любых трех точек A, B, C ∈ A имеет место равенство:

Векторное пространство V называется направляющим пространством аффинного пространства A , или — пространством переносов аффинного пространства A .

Заметим во избежание недоразумений, что отображение принадлежит векторному пространству: v (A, B) ≡ AB ∈ V , а не аффинному пространству A — пространству точек.

Данная аксиома означает, что определена операция сложения элементов пространства A с векторами из пространства V .

Некоторые свойства аффинного пространства.

1) Каждой паре совпадающих точек из A сопоставляется нулевой вектор из V .

Доказательство. Пусть М A и MM = z . Пусть x — произвольный вектор из V по аксиоме 1: точка N A : MN = x . По аксиоме 2: z + x = MM + MN = MN = x z = MM = 0.

2) Если AB = , то BA = – .

Доказательство. Пусть BA = y x + y = AB + BA = AA = 0 y = – x .

Векторы сравниваются движением параллельного смещения по пространству.

Два вектора сравнимы, если они параллельны. Результат сравнения имеет три взаимоисключающих значения: меньше, равно и больше.

Не параллельные векторы не сравнимы, потому что нет такого движения.

Метрика в аффинном пространстве не определена. Но некоторые элементы метрики в ней можно усмотреть. См. «Метрика».

1.2 Аффинные координаты

По аналогии с понятием линейной независимости векторов вводят понятие аффинной независимости точек аффинного пространства. Именно: точки P ₀ , P ₁ , P ₂ , … P _n называют аффинно зависимыми, если какую-либо из них, например — P ₁ , можно представить в виде барицентрической комбинации остальных точек. В противном случае эти точки называются аффинно независимыми.

Условию аффинной независимости точек можно придать иную форму: справедливо предложение, по которому точки аффинного пространства аффинно независимы тогда и только тогда, когда не существует нетривиальной сбалансированной комбинации данных точек, равной нулевому вектору.

Любое из максимальных аффинно независимых множеств точек аффинного пространства можно трактовать как точечный базис (перенумеровав данные точки тем или иным способом). Всякую точку пространства можно представить в виде барицентрической комбинации точек, входящих в точечный базис; коэффициенты этой комбинации называют барицентрическими координатами рассматриваемой точки.

Рассмотрим n – мерное аффинное пространство A и введём в нём так называемую аффинную систему координат. Пусть О – точка в A – начало координат и пусть e₁, …, e_n − базис в соответствующем пространстве V _n . Пусть М – произвольная точка A . Тогда определён вектор OM Î V _n , называемый радиус-вектором точки М. Разлагая OM по e₁, …, e _n , имеем: OM = x 1 e ₁ +…+ x n e_n .

Коэффициенты x 1 , … x n этого разложения называются аффинными координатами точки М (относительно выбранной системы координат с началом в точке О и базисом e₁, …, e_n ). Система <0, e₁, …, e_n > называется репером.

Ввиду единственности разложения вектора по базису, координаты точки определяются однозначно.

Пусть да на другая точка N с координатами ( y 1 , … y n ). Из аксиомы 1) аффинного пространства Þ MN = MO + ON = ON – OM = ( y 1 — x 1 )e₁ +…+ ( y n — x n ) e_n , т.е. вектор MN и меет координаты ( y 1 — x 1 , …, y n — x n ), т.е., чтобы получить координаты вектора MN надо из координат конца вычесть координаты начала.

Замечание 1. Пусть выбран базис и начало координат перенесено из точки О в точку О’. Пусть координаты О’ в базисе с центром в О заданы координатами a 1 , … a n . Тогда имеем OM = OO ’ + OM ’ Þ x i = a i + x ’ i .

Замечание 2. Если О = О , а базис < e > переходит в базис < e ’ _i > : E ’ = E Þ X = X ’.

В общем случае, .

1.3 Инварианты аффинного пространства

Аффинное пространство является однородным, масштабно инвариантным и изотропным в силу определения: любые n ≤ N +1 ( N – размерность пространства) независимых точек аффинного пространства можно отобразить в такое же количество других точек аффинным преобразованием. Однородное преобразование соответствует смещению начала координат, масштабное – масштабному преобразованию координат, изотропное – любому линейному преобразованию координат.

Геометрическими инвариантами аффинного пространства являются точки, прямые, плоскости, … При любых линейных преобразованиях координат эти геометрические фигуры остаются ими же. Да и любой другой аффинный объект при аффинном преобразовании сохраняет свою инвариантность. Но не всякий объект является аффинным. Многие геометрические объекты евклидова пространства не являются аффинными. Например, понятия «окружность» и «квадрат» в аффинном пространстве определить невозможно. Аффинное пространство не дружит с длинами (расстояниями) и углами.

Инвариантами аффинного пространства являются свойства сравнимости: эквивалентности, подобия и различимости.

Инвариантом аффинного пространства является свойство параллельности объектов, если это свойство к ним применимо.

Интересным и общим инвариантом аффинного пространства является отношение разностей координат между любыми тремя точками на прямой:

где j ( A ) – аффинное преобразование.

1.4 Отличие аффинного пространства от евклидова

Аффинное пространство очень близко к евклидовому, их можно взаимно однозначно отобразить друг на друга, причем параллельные прямые останутся параллельными прямыми. Они оба бесконечные и произвольной размерности. Они однородные. Они изотропные. Они являются векторными пространствами. В них можно определить свободные и связанные векторы. А также скаляры, векторы, тензоры … В них определены точки, прямые, плоскости, … Но в нем нет понятия скалярного произведения, аффинное пространство не является метрическим пространством и во многом его свойства из-за этого другие. Свертка тензоров формально определена как линейное преобразование элементов тензора при преобразованиях координат. Определено даже скалярное произведение (точнее – свертка) и соответствующий ей билинейный тензор, выделяющий в пространстве некоторую систему координат и который можно использовать для поднятия-опускания индексов, но без связи с метрическим тензором.

1. В евклидовом пространстве сравнение происходит смещением и линейным ортонормированным преобразованием (поворот). Параллельное перемещение (смещение) и масштабное преобразование – частные случаи линейного преобразования.

В аффинном пространстве ортонормированный поворот не определен. Сравнение объектов в аффинном пространстве происходит линейным преобразованием типа смещение.

Подобные объекты определяются линейным преобразованием координат пространства -масштабным или общего типа.

2. Определены метрические понятия «расстояние», «длина», «скалярное произведение векторов», свертка тензоров.

Существенным отличием является отсутствие понятия расстояния, длины. В связи с этим для тензоров невозможно определить поднятие и опускание индекса. Все индексы либо наверху, либо внизу. Свертку по разным индексам формально можно определить, но без привязки к метрике.

Но сравнивать параллельные векторы возможно, и даже на их множестве (параллельных векторов) можно определить метрику и соответствующее тензорное исчисление.

3. Имеется понятие «угол».

Не определяется понятие «угол». Единственный измеримый угол – нулевой. В связи с этим возможно определение только понятия параллельности векторов и определение класса «параллельных векторов», а также «пространства эквивалентных векторов». Свойство параллельности векторов в аффинном пространстве не зависит от конкретного пути перемещения (путем смещения) сравниваемых векторов, но может зависеть в локально аффинном пространстве.

4. Можно сравнивать длины произвольных векторов.

Сравнить длины не параллельных векторов невозможно, потому что не определено понятие изометрического поворота.

2 Метрика и аффинное пространство

2.1 Определение

Метрика пространства определяется числовым отношением l ( x , y )≥0 между произвольными элементами пространства x и y , удовлетворяющее следующим аксиомам:

l (x,y) = l(y,x) ≥ 0,

где l ( x , y , z ) – общая длина отрезков линии, проходящих через три точки x , y , z ,

l ( x , y ) — длина отрезка этой же линии между точками x и y ,

l ( y , z ) — длина отрезка этой же линии между точками y и z .

У этих аксиом имеется еще одно неявное предположение – одинаковые расстояния эквивалентны или расстояния сравнимы. Или если понятнее – метрика определена через один и тот же эталон. Сравнимость определяется через существование изометрического преобразования.

Для прямой аксиома треугольника становится эквивалентной третьей аксиоме.

Метрика позволяет определять базу окрестностей топологического пространства через ее диаметр.

Евклидово пространство полностью удовлетворяет этим аксиомам. При нарушении некоторых из этих условий получаются более слабые метрики. Например, в пространстве Минковского нарушаются первая и третья аксиомы. Но это не делает ее менее полезным при учете этой особенности. В аффинном пространстве изначально метрика не определяется.

Через метрику можно определить длину любой линии. Но для этого необходимо, чтобы общая длина линии на любом участке для любой линии была интегрируема (следствие аксиомы № 2). Это возможно, если метрика на прямых будет интегрируемой, а это так в соответствии с третьей аксиомой метрики.

При определении метрики можно определить прямую линию между двумя точками как линию наименьшей длины между ними. Такая линия называется геодезической . Сказать, что эта линия прямая, нельзя. Мы не связывали эту метрику с аффинной связностью.

2.2 Метрика в аффинном пространстве

Метрика в аффинном пространстве явно не определена. Но в ней можно определить наведенную «числом» метрику, причем на каждой прямой, даже более – на классе параллельных векторов и прямых можно определить метрику, удовлетворяющую всем аксиомам метрики. Для этого необходимо

1). Определить эталонный вектор и предположить, что

2). эталонный вектор имеет единичную (скалярную) длину.

3). Все одинаковые векторы имеют одну и ту же длину. Векторы сравниваются движением параллельного смещения. Движение предполагается изометрическим.

4). Длина произвольного вектора определяется количеством прикладываний эталонного вектора на измеряемый. Длина меньшего чем эталонный вектора определяется долями эталонного вектора.

5) Длина обратного вектора равна длине прямого.

*Интересной альтернативой последнему условию является неравенство длин противоположных векторов.

У этой метрики имеются прямые следствия:

Следствие 1. Длина вектора определяется положительными целым, дробным или вещественным числами.

Следствие 2. Т.к. все сравнимые векторы параллельны, длина определена на классе параллельных векторов и отрезков прямых.

На векторах прямой линии можно определить понятие верхнего и нижнего индексов и операцию поднятия и опускания индексов: но на прямой только один индекс. Противоположные векторы могут при этом иметь ту же длину.

Но сравнить не параллельные векторы и отрезки невозможно. Несмотря на то, что расстояние определено между любыми двумя точками. Потому что между ними не существует изометрического преобразования. Даже можно составить треугольник из трех отрезков прямых с определенной «численной» длиной, но аксиома треугольника к ним не применима из-за несравнимости «численных» длин отрезков. На разных прямых будут действовать разные, точнее, не связанные между собой, эталоны длины. Даже на разных направлениях на прямой могут быть разные эталоны. Мы можем определить эталоны на каждой прямой, но не может их сравнивать.

Следствие 3. Аффинное пространство, кроме размерности 1, даже при определенности расстояния между любыми двумя точками, может быть и не метрическим.

Можно ли аффинное пространство сделать метрическим? Конечно, можно.

Например, волевым решением. Для этого необходимо принять, что все эталоны на разных прямых эквивалентны. После этого все векторы одного численного значения будут изометрическими. Концы векторов с общим началом будут определять сферу определенной размерности и радиуса. Поворот вектора можно определить как движение конца вектора по этой сфере.

Недостаток этой метрики – эталоны на разных прямых абсолютно независимы, хотя и на каждой прямой связаны аффинной связностью. Как следствие, возможная «ежистость», не дифференцируемость поверхности сферы.

2.3 Поворот вектора в аффинном пространстве

Под поворотом вектора понимается изометрическое движение связанного вектора, изменяющее ее направление, но не изменяющее ее начало и длину. Это также означает, что после нескольких последовательных поворотов вектор также не изменяет своей длины. при возврате в исходное положение вектор должен совместиться с самим собой. Но как определить поворот в аффинном пространстве, где нет длины?

Эта проблема решаема тривиально на классе параллельных векторов заданием одного эталонного вектора единичной длины. Она также решаема волевым решением задания метрической функции R ( a , b ) на множестве всех векторов или эталонной единичной сферы при соблюдении некоторых условий (см. выше). В любом случае эта метрика должна удовлетворять аксиомам метрики.

Определенная в пространстве метрика в каждой точке пространства определяет изометрическую поверхность «сфера». Поверхность этой сферы задается функцией, согласованной с метрической функцией:

R ( r i ) = R .

где R = const – радиус сферы. Эта метрическая функция линейна по r :

Т.к. мы занимаемся аффинным пространством, необходимо, чтобы поворот оставлял прямые прямыми. Это очень сильно ограничивает возможные виды метрической функции R . А это возможно только в том случае, когда преобразование координат происходит линейно. Это также значит, что параметр поворота j i _j не должен зависеть от самого вектора a j .

Для произвольной координатной системы n -мерного аффинного пространства имеется всего n × n = n 2 параметров тензора поворота. Предположение, что после нескольких последовательных поворотов вектор не изменяет своей длины и при возврате в исходное положение должен совместиться с самим собой означает, что детерминант матрицы поворота должен быть равен единице:

Для одномерного аффинного пространства может существовать только единственный тензор поворота – это одноэлементный тензор j i _j = |1|. Это тождественное преобразование и инверсия.

Интересно рассмотреть бесконечно малые повороты векторов. Они задаются тензором бесконечно малого поворота d j i _j .

Само изменение координат da i _j повернутого вектора в этом случае определяется формулой

1) Антисимметричные члены соответствуют координатному вращению, при этом координатный объем объектов при бесконечно малом повороте не изменяется. Такой поворот соответствует тригонометрическому (т.е. обычному) ортогональному координатному повороту.

2) Симметричные недиагональные члены соответствуют координатному смещению пространства, при этом координатный объем объектов при бесконечно малом повороте также не изменяется. Такой поворот соответствует гиперболическому координатному повороту.

3) Диагональные члены соответствуют масштабным деформациям координатных осей. Такой поворот собственно не является поворотом. При этом может изменяться объем объектов. Неизменности объема при бесконечно малом масштабном преобразовании соответствует равенству нулю суммы всех диагональных членов, и это условие является необходимым условием общего изометрического поворота.

Поворот в каждой плоскости можно представить тензором dT i _j :

с четырьмя образующими:

Первые три образующие являются изохорными образующими. Первый к тому же является изометрическим образующим. Четвертый элемент является не изометрическим и даже не изохорным образующим. Он соответствует общему масштабному преобразованию.

3-мерный поворот чисто технически можно представить как 3 поворота в трех взаимно независимых плоскостях. 3-мерный поворот имеет следующие образующие:

Из представленных 6 элементов все 6 являются независимыми.

Масштабное преобразование имеет следующие образующие:

Из представленных 6 элементов независимыми являются только 3 элемента. Это следующие три после их выделения из представленных путем сложения половинных верхних и нижних строк элементов:

Для изометрических преобразований имеется условие – детерминант матрицы преобразования должен быть равен единице. Общая матрица поворота следующая:

Ее детерминат при любых значениях a , b , g равен 0.

Обратите внимание: для ортонормированного евклидова пространства количество независимых элементов матрицы поворота равно трем! И они соответствуют антисимметричным образующим матрицы поворота.

Несмотря на то, что изометрический поворот мы рассмотрели, начав с определения эталона длины, сам поворот не нуждается в ее наличии. Эталон можно выбрать произвольно, инвариантом поворота остается отношение длин векторов. При этом диагональные элементы равны нулю.

3 Локально аффинное пространство

Локально аффинное пространство — это аналог риманова пространства по отношению к евклидовому.

Рассмотрим пространство, размеченное достаточно произвольным, но все же непрерывным образом. Исходно оно может быть линейным аффинным пространством, но не обязательно. Даже непрерывная разметка исходно аффинного пространства не гарантирует прямолинейность линий, задаваемых линейными функциями в полученном пространстве. Но локально в бесконечно малой окрестности произвольной точки его можно считать линейным аффинным пространством, потому что прямые в этой бесконечно малой окрестности задаются линейными функциями. Точно так же бесконечно малая окрестность произвольной точки риманова пространства является евклидовой.

Если оно однородно, то для любых двух точек пространства можно найти отображение, переводящее параллельные прямые и векторы бесконечно малой окрестности одной из точек в параллельные прямые и векторы бесконечно малой окрестности другой точки. Такое пространство назовем локально аффинным.

Главная задача для локально аффинного пространства – вопрос о сравнении векторов. Для линейного аффинного пространства ответ на этот вопрос тривиален. В координатном представлении два вектора эквивалентны, если они имеют одинаковые координаты относительно своих начал. Для локально аффинного пространства ответ на этот вопрос совсем не тривиален: одинаковые координаты векторов относительно своих начал не гарантируют их эквивалентность. Эквивалентность векторов в локально аффинном пространстве определяется через аффинную связность, через которую можно определить эквивалентность векторов. Кроме единственного тривиального случая – когда их начала совпадают.

*Далее мы будем рассматривать только непрерывно размеченные (координатные, возможно, кусочно-сшитые) гладкие пространства с дифференцируемыми в ней функциями, возможно, за исключением некоторых граничных подмножеств меньшей размерности (точки, линии, поверхности, …).

3.1 Аффинная связность

Связность линейного аффинного пространства тесно связана с параллельностью и сравнимостью параллельных векторов между собой в различных точках. Т.е. два вектора связны, если они параллельны и равны. Параллельные векторы линейно аффинного пространства a i и b i определяются отношением

Для равных векторов коэффициент равен 1, т.е. » i : a i = b i . Связать каким либо скалярным отношением два не параллельных вектора не представляется возможным.

Встает вопрос: можно ли сравнить два произвольных вектора? Как мы выяснили, в одной точке можно сравнить только параллельные векторы. Для сравнения векторов в разных точках необходимо переместить их в одну и ту же точку. Дополнительный вопрос: как переместить вектор из одной точки в другую точку? Простое координатное смещение не подходит, потому что даже 2 равных вектора исходно аффинного пространства после преобразования координат получают разные координаты.

Для сравнения двух связанных векторов можно определить следующую операцию. Возьмем две бесконечно близкие точки. Переместим произвольный вектор a i между этими точками параллельно самому себе. Это возможно сделать на бесконечно малом участке, при условии, что малому перемещению вектора будет соответствовать и малое изменение параметров перемещенного вектора в новой точке. Это изменение da i должно быть линейно по малому перемещению dr j и самому вектору a k :

Объект называется тензором аффинной связности локально аффинного пространства . Для произвольной связности 3-мерного пространства количество элементов равно 3 × 3 × 3 = 27. Из 27 параметров независимыми являются только (1+2+3) × 3 = 18, т.к. по нижним индексам связность симметрична или ее всегда можно симметрировать. Для произвольной связности 4-мерного пространства количество элементов равно 4 × 4 × 4 = 64. Из 64 параметров независимыми являются только (1+2+3+4) × 4 = 40.

Для линейного и циклического аффинного пространств все коэффициенты равны нулю, потому что da i тождественно равно нулю. Но не всякое пространство с тождественными нулю коэффициентами связности являются линейными аффинными пространствами. Например, цилиндр не является линейным аффинным пространством.

Сравнивать удаленные векторы можно, перемещая вектор параллельно себе самому вдоль некоторой траектории. Но при этом может возникнуть определенная трудность. При параллельном перемещении по разным траекториям вектор может занимать разные новые направления в конечной точке.

Трудность может возникнуть и при сравнении вектора с самим собой: при перемещении по замкнутому контуру можно получить параллельный, но не равный исходному вектор. Абсурд. Но к бесконечно близкому перемещению это не относится.

На основании аффинной связности определяется понятие прямой линии . Прямая линия обладает тем свойством, что вектор, параллельный ей в одной из точек этой линии, параллелен ей и в любой другой точке при перемещении вдоль нее.

Процедура параллельного самому себе перемещения вектора может говорить и о том, что не изменяется также и ее длина. Оно определяется существованием наведенной на классе параллельных (эквивалентных) векторов метрикой. Следовательно, аффинная связность как-то связана с метрикой.

3.2 *Метрика и аффинное пространство

Метрику можно связать с аффинной связностью. Эта метрика определяется метрикой на прямых линиях и параллельных векторах. Условием определения такой метрики будет равенство длин равных после переноса вдоль прямой линии связанных с ним и параллельных ей (касательных к ней) векторов. На векторах прямой линии можно определить понятие верхнего и нижнего индексов и операцию поднятия и опускания индексов: но на прямой только один индекс. Противоположные векторы могут при этом иметь ту же (или другую тоже?) длину. Но: даже при одинаковых численных значениях длин двух векторов на разных прямых сказать, что они равны, нельзя. Определенным нами движением невозможно их сравнить. На разных прямых будут действовать разные, точнее, не связанные между собой, эталоны длины. Даже на разных направлениях на прямой могут быть разные эталоны. Мы можем определить эталоны на каждой прямой, но не может их сравнивать.

Расширить метрику до класса параллельных векторов можно, если в пространстве возможно определение класса параллельных векторов, получаемых произвольным параллельным движением определяющего вектора. Необходимым и достаточным условием будет условие неизменности вектора от конкретного пути движения. На каждом таком классе возможно определение единого эталона. А также определение параллельных прямых линий. Здесь тоже возможно «силовое» решение.

Не всякое пространство допускает такое. Не на каждом пространстве возможно определение класса параллельных векторов, кроме тождественного. Линейное аффинное пространство является одним из таких пространств. Такими являются также циклические аффинные пространства. В локально аффинном пространстве общего типа необходимое и достаточное условие может не выполняться.

Но этими способами невозможно сравнить длину двух не параллельных векторов даже в одной и той же точке. Для такого сравнения необходимо разрешить поворачивать вектор до положения параллельности с другим вектором в точке нахождения или определить другой механизм поворота. Например, «силовой» или « волевой » механизм. Для этого необходимо принять, что все эталоны на разных прямых эквивалентны. После этого все векторы одной длины будут изометрическими. Концы векторов с общим началом будут определять сферу определенной размерности и радиуса. Поворот вектора можно определить как движение конца вектора по этой сфере.

Если бы у нас была возможность определить единый эталон длины в каждой точке для каждого направления, выходящего из нее, можно было бы определить метрику на любых кусочно-прямолинейных линиях как наведенную на ее прямолинейных кусках метрику от прямой линии, содержащей ее. А также можно было бы определить метрику и на произвольной линии как наведенную на ее бесконечно малых участках от прямой линии, касающейся ее на этом участке, при условии их дифференцируемости. Ее можно назвать касательной мерой линии.

3.3 *Поворот вектора в аффинном пространстве

Под поворотом вектора понимается изометрическое движение связанного вектора, изменяющее ее направление, но не изменяющее ее начало и длину. Но как определить поворот в аффинном пространстве, где нет длины?

Но эта проблема решаема на классе параллельных векторов. Она также решаема волевым решением задания метрической функции R ( a , b ) на множестве всех векторов при соблюдении некоторых условий. В любом случае эта метрика должна удовлетворять аксиомам метрики.

Определенная в пространстве метрика в каждой точке аффинного пространства определяет изометрическую поверхность «сфера». Поверхность этой сферы задается согласованной с метрической функцией функцией

Более об этой функции ничего нельзя сказать, потому что форма сферы может быть произвольной и напоминать собой ежика. Т.е. поверхность сферы может быть не гладкой, не дифференцируемой или даже не непрерывной. Если попроще, может оказаться так, что концы близких иголок этого ежика могут находиться не близко. Для удобства анализа полученной метрики необходимо принять, что поверхность сферы является дифференцируемым многообразием. Если эта функция гладкая, то метрическая функция при r ® 0 с точностью до первого порядка малости будет линейна по r :

где d j i _j — бесконечно малый поворот в плоскости ( i , j ). При этом d j i _j не должен вырождаться в просто деформацию.

Но об изменении конкретного вектора a j при перемещении на бесконечно малый угол d j i _j что-то можно сказать. Это изменение da i должно быть линейно по самому вектору a j и перемещению на бесконечно малый угол d j i _j :

Поворот должен осуществляться так, чтобы прямые оставались прямыми. А это возможно только в том случае, когда преобразование координат происходит линейно. А это значит, что параметр d j i _j не должен зависеть от самого вектора a j . Для произвольной метрической связности 3-мерного пространства имеется всего 3 × 3 = 9 параметров. Изометрический поворот как условие на элементы d j i _j предполагает уменьшение на три единицы количества независимых элементов матрицы вращения – остается 6 элементов. Из них 3 — собственно вращения и 3 — деформации. Конечно, координатные.

2) Симметричные недиаглнальные члены соответствуют координатному смещению объектов, при этом координатный объем объектов при бесконечно малом повороте также не изменяется. Такой поворот соответствует гиперболическому координатному повороту.

3-мерный поворот чисто технически можно представить как 3 поворота в трех взаимно независимых плоскостях. Поворот в каждой плоскости можно представить тензором dT i _j :

с четырмя образующими:

Но случай локально линейного аффинного пространства интересен тем, что в ней в некоторых случаях можно определить не тривиальный поворот вектора перемещением вдоль замкнутой линии с возвращением в исходную точку с изменением направления вектора.

источники:

http://matica.org.ua/metodichki-i-knigi-po-matematike/algebra-i-geometriia-tolstikov-a-v/47-affinnaia-sistema-koordinat-na-priamoi-ploskosti-i-v-prostranstve

http://lowsofphisics.ru/matyematika/affinnoye_prostranstvo.htm