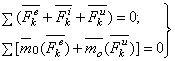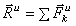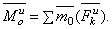Уравнения кинетостатики для механической системы

Техническая механика

Основы кинетостатики

Метод кинетостатики в динамике.
Принцип Даламбера

Как известно, первый закон Ньютона гласит, что любое тело, любая материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения, пока какая-нибудь сила не нарушит это состояние. Этот закон называют законом инерции, а свойство материальных тел «неохотно» изменять свое текущее состояние покоя – инертностью.

Явление инертности использовал в идее оригинального принципа динамических расчетов французский ученый Ж. Д’Аламбер (д’Аламбер, Даламбер; фр. Jean Le Rond D’Alembert, d’Alembert, 1717-1783) , по имени которого этот принцип и назван.
Принцип Д’Аламбера (Даламбера) широко применяется для решения задач динамики методами кинетостатики.

Справедливости ради, следует отметить, что несколько раньше Д’Аламбера возможность решения задач динамики с помощью приемов статики изучали такие видные российские ученые Петербургской Академии наук, как Я. Герман и Л. Эйлер, жившие примерно в одно время с Даламбером.

Итак, что же такое принцип Д’Аламбера и чем он может быть полезен при решении задач динамики?

Сначала вспомним статику, где все легко и просто – любое тело или материальная точка будет находится в равновесии, если действующие на него силовые факторы уравновешивают друг друга. Все очевидно, просто и понятно. Благодаря приемам статики можно определить неизвестные активные или реактивные силы, действующие на уравновешенное тело или точку, применив простые математические приемы и геометрические построения.
Нельзя ли эти приемы использовать для подвижных тел, причем не просто подвижных, а движущихся с ускорением? Оказывается можно, а иногда даже просто необходимо, как указал знаменитый француз, увековечивший свое имя в известном потомкам принципе.

Представим себе материальную точку массой m движущуюся с ускорением a под действием какой-то системы активных и реактивных сил, равнодействующая которых равна F .
Воспользуемся вторым (основным) законом динамики для того, чтобы уравнение движения этой точки записать в форме уравнений равновесия:

Выражение, стоящее в скобках называют силой инерции , и обозначают F ин .
Итак:

Сила инерции есть вектор, равный произведению массы материальной точки на ее ускорение в данный момент времени, и направлен в сторону, противоположную ускорению .
На основании этого определения можно записать:

F + F ин = 0 или Σ(F, F ин ) = 0 .

Это равенство и является математическим выражением принципа Д’Аламбера, который формулируется так: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющих всем условиям равновесия .
Т. е. Д’Аламбер предложил оригинальный способ применения методов статики к движущимся материальным точкам, использовав при этом в качестве основного инструмента понятие инертности и силы инерции.

Утверждение, что тело якобы находится в состоянии равновесия во время ускоренного движения, может вызвать недоумение. Как это может быть?
Здесь следует отметить, что сила инерции, введенная в научную терминологию Д’Аламбером, является понятием условным, т. е. фактически такой силы в природе не существует, в отличие от понятия инертности — свойства любых материальных тел и точек, проявляющееся в стремлении сохранять свое состояние. Но именно условное уравновешивание силой инерции движущихся с ускорением тел, позволило использовать при решении задач динамики приемы статики, породив раздел теоретической механики — кинетостатику.

Явление инертности (инерции) можно пояснить на таком простом примере. Если подвесить на нити груз, который она легко выдержит в статическом состоянии, а затем резко дернуть за конец нити, то она порвется именно благодаря инертности груза.
Другой пример: если тяжелое чугунное ядро попытаться сдвинуть с места, то потребуется приложить немалое усилие, чтобы оно покатилось. Когда же ядро, наконец, покатилось, для его остановки потребуется, опять же, немалое мускульное усилие.
В каждом из этих случаев наглядно проявляется свойство инертности материальных тел.

Пример решения задачи методом кинетостатики

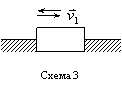
Задача: в кабине лифта размещены пружинные весы, на которых установлен груз. Когда кабина неподвижна показание весов составляет 50 Н, а при движении лифта показание весов увеличилось до 51 Н.
Определить, с каким ускорением движется кабина лифта.

Решение.
Применим к телу принцип освобождаемости, отбросим пружинные весы и заменим их реакцией R , равной натяжению пружины. Для решения задачи применим метод кинетостатики, т. е. приложим к телу силу инерции F ин .
Составим уравнение равновесия взвешиваемого тела, спроецировав все силы на вертикальную ось y ; предполагаем, что ускорение а кабины направлено вверх, и, следовательно, сила инерции направлена вниз (т. е. в противоположную ускорению сторону):

ΣY = 0 ; R – G – F ин = 0 .

Модуль силы инерции определяем по формуле:

Подставив это выражение в уравнение, определим ускорение:

a = (R – G)g/G = (51 – 50)×9,81/50 = 0,196 м/с 2 .

Ускорение получилось положительным, следовательно мы изначально правильно предположили, что оно направлено вверх (если бы получилось отрицательное значение, значит ускорение направлено вниз).

Силы инерции в криволинейном движении

В криволинейном движении точки полное ускорение равно векторной сумме касательного (тангенциального) и нормального (центростремительного) ускорений.

Касательное ускорение определяется по формуле a_τ = dv/dt , нормальное ускорение a_n = v 2 /ρ , полное ускорение a = √(a_τ 2 + a_n 2 ) .

Каждому ускорению соответствует своя сила инерции:

• Касательная (тангенциальная) сила инерции: F_τ ин = mdv/dt ;
• Нормальная (центробежная) сила инерции: F_n ин = mv 2 /ρ ;
• Полная сила инерции: F ин = ma .

В качестве примера рассмотрим равномерное движение по окружности, лежащей в горизонтальной плоскости, камня силой тяжести G , привязанного невесомой нитью длиной r , расположенной в той же плоскости (рис. 1) .
Чтобы нить оставалась в плоскости движения камня, предполагается, что он скользит по идеально гладкой горизонтальной плоскости.
Скорость движения камня обозначим v .

Тогда F_n ин = mv 2 /ρ — центробежная сила инерции (эта сила натягивает нить) ; R = mv 2 /ρ — центростремительная сила, приложенная к камню (эта сила удерживает камень на круговой траектории) .
Обе эти силы, согласно второму закону Ньютона, равны по модулю и направлены в противоположные стороны, т. е. уравновешивают друг друга.
Очевидно, что касательная сила в данном примере будет равна нулю, поскольку камень движется равномерно ( а_τ = 0 ).

Из опыта известно, что при достаточной скорости камня нить может не выдержать и разорваться, тогда камень полетит по касательной к окружности, т. е. по направлению имеющейся в момент разрыва нити скорости. Это доказывает, что центробежная сила инерции есть реальная сила для связи, но к телу она приложена условно.

Внутри тел, движущихся с ускорением, также возникают внутренние силы инерции, так как для каждой частицы тела соседние являются связями.

Найдем, чему будет равно натяжение нити, если камень движется по окружности, лежащей в вертикальной плоскости (рис. 2) . Для определения натяжения R нити применим принцип Д’Аламбера, т. е. приложим к камню нормальную силу инерции F_n ин и касательную силу инерции F_τ ин .

Спроецируем все силы в направлении нити, в результате чего получим:

R – G cosα – F_n ин = 0 , откуда: R = F_n ин + G cosα = mv 2 /r + G cosα .

Очевидно, что натяжение нити будет максимальное при α = 0, т. е. когда камень находится в нижнем положении:

Минимальное натяжение нити имеет место, когда α = π рад, т. е. в тот момент, когда камень находится в верхнем положении:

Следует отметить, что под влиянием силы тяжести в данном случае модуль скорости камня будет изменяться от максимума в нижнем положении до минимума в верхнем положении.

Если выразить линейную скорость камня через угловую скорость нити, используя зависимость v = ωr , то формула центробежной силы примет вид:

Пример решения задачи с использованием принципа Д’Аламбера

Задача: определить скорость v искусственного спутника Земли, движущегося по круговой орбите на высоте h = 230 км от поверхности Земли, радиус которой принять равным R = 6370 км.
Изменением ускорения свободного падения и сопротивлением атмосферы пренебречь.

Решение.
После того, как ракета-носитель вывела спутник массой m на орбиту и сообщила ему скорость v , направленную по касательной к орбите, спутник продолжает движение под действием одной лишь силы притяжения Земли.
Для определения скорости v спутника применим принцип Д’Аламбера, т. е. приложим к спутнику центробежную силу инерции и составим уравнение равновесия, спроецировав все силы на ось, проходящую через спутник и центр Земли:

Так как F_n ин = mv 2 /(R + h) , то можно записать: mg — mv 2 /(R + h) = 0 .

Сократив члены этого равенства на m (массу спутника) , получим:

Подставив значения, получим: v = √[9,81(6370 + 230)1000] ≈ 8000 м/с ≈ 8 км/с .

Уравнения кинетостатики для механической системы

Лекция 4. Силовой ( кинетостатический ) анализ механизмов.

Общие сведения и определения

Проектирование нового механизма всегда включает его силовое исследование, так как по найденным силам производится последующий расчет на прочность элементов кинематических пар и звеньев механизма.

При проведении силового анализа решаются основные задачи:

1. Определение реакций в кинематических парах механизмов, находящихся под действием заданных внешних сил. Эти реакции затем используются для расчёта звеньев и элементов кинематических пар (например, подшипников) на прочность, жёсткость, долговечность и т.д.

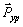
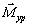
2. Определение уравновешивающей силы или уравновешивающего момента , приложенных к ведущему звену. Они уравновешивают внешние силы, приложенные к механизму. Эти величины нужны, например, для выбора двигателя, приводящего в движение данный механизм.

3. Дополнительно выясняют вопросы об уравновешенности механизма, износе его звеньев, о потерях на трение в отдельных кинематических парах, о коэффициенте полезного действия механизма в целом и др.

При силовом анализе, кроме основной (полезной) нагрузки на рабочий орган, необходимо учитывать силы тяжести звеньев, их силы инерции, силы трения в кинематических парах.

Силовой расчет ведется методом кинетостатики. В отличие от статического , кинетостатический расчет механизмов наряду с внешними силами (движущими силами, силами полезных и вредных сопротивлений, силами тяжести) учитывает и силы инерции масс звеньев.

Метод кинетостатики основан на принципе Даламбера, который применительно к механизмам можно сформулировать так: если ко всем внешним силам, действующим на систему звеньев, добавить силы инерции, тогда под действием всех этих сил система звеньев может условно считаться находящейся в равновесии.

При кинетостатическом расчете кинематическая цепь механизма разбивается на группы Ассура , которые являются статически определимыми. Расчет ведется путем последовательного рассмотрения условий равновесия отдельно каждой группы, начиная с наиболее удаленной от исходного механизма (ведущего звена), последним рас c читывается ведущее звено.

При рассмотрении условий равновесия группы без учета силы трения составляющие реакции во внешней вращательной паре представляются направленными по звену (нормальная реакция) и перпендикулярно звену (тангенциальная реакция) и приложены они в центре шарнира, во вращательной паре подлежат определению величины и направления нормальной и тангенциальной реакций.

В поступательной паре, в общем случае, подлежат определению величина и точка приложения реакции, так как известно только то, что направление реакций всегда перпендикулярно оси направляющих пары.

Анализ свойств механизма можно получить путем исследования каждой группы Ассура через 10 градусов (20 градусов или 30 градусов) угла поворота кривошипа. В этом случае выявляется полная картина силового нагружения всех подвижных соединений механизма и звеньев за цикл движения машины.

Цикл – промежуток времени, по истечении которого все кинематические параметры принимают первоначальное значение, а технологический процесс, происходящий в рабочей машине, начинает повторяться вновь.

Классическая задача силового анализа механизма обычно решается при таких исходных данных:

1) Кинематическая схема механизма.

2) Размеры и иные геометрические параметры звеньев.

3) Законы движения входных звеньев.

4) Массы и моменты инерции звеньев.

5) Силы и моменты полезных сопротивлений.

В дальнейшем будем считать, что к моменту начала силового расчета механизма выполнен его полный кинематический анализ и рассчитаны веса звеньев, их инерционные силы и моменты, а силы и моменты полезных сопротивлений заданы.

Этапы кинетостатического расчёта

Различают два этапа кинетостатического расчёта:

— Расчёт механизма без учёта потерь на трение в кинематических парах.

— После конкретного конструирования узлов производится дополнительный расчёт потерь мощности в кинематических парах на преодоление трения.

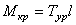
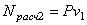
Итогом кинетостатического расчёта является определение движущей силы на ведущем звене, которая даёт возможность определить крутящий момент по формуле и мощность, по формуле: .

Полная мощность определяется по формуле: 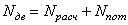. По значению полной мощности выбирается мощность двигателя.

Порядок проведения кинетостатического расчёта:

1. Определение степени подвижности механизма.

2. Для каждого отдельного положения механизма внутри цикла его работы строятся планы скоростей и планы ускорений. С помощью планов ускорений определяются ускорения центров масс.

3. Механизм раскладывается на структурные группы Ассура .

4. Производится кинетостатический расчёт отдельных структурный групп начиная с последней , постепенно приближаясь к ведущему звену.

5. Кинетостатический расчёт ведущего звена.

6. Определение крутящего момента или движущей силы на ведущем звене.

7. Определение мощности двигателя.

8. Пункты 4-7 повторяются для множества положений механизма за полный цикл его работы.

9. Выбираются наибольшие значения мощности и усилий, действующие в кинематических парах.

10. На основании полученных данных составляется задание на проектирование.

Силы, действующие в механизмах

Различают две группы внешних сил.

Движущие силы Р_дв или моменты движущих сил М_дв , которые:

— совершают положительную работу;

— направлены в сторону скорости точки приложения силы или под острым углом к ней;

— задаются посредством механической характеристики двигателя.

Пример: силы давления газа на поршень в двигателе внутреннего сгорания, силы веса при опускании груза и т.д.

Силы сопротивления Р_С и их моменты М_С, которые:

— совершают отрицательную работу;

— направлены противоположно скорости.

В свою очередь силы сопротивления делятся на силы:

— полезного сопротивления Р_{п .с} и моменты М_п.с (силы тяжести при подъеме груза);

— вредного сопротивления: трение в кинематических парах, сопротивление среды, внутреннее сопротивление (например, силы упругости звеньев).

Кроме этого существуют:

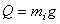
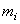
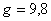
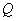
— силы веса (тяжести) , где – масса звена в кг; м/с 2 – ускорение свободного падения. При кинематическом исследовании считают, что сила тяжести приложена в центре тяжести звена. Если звено выполнено в виде стержня, то его ц.т . расположен в центре симметрии звена, а если в виде ползуна, то в центре шарнира. Силы тяжести в течени и расчётного цикла могут быть как движущими, так и силами полезного сопротивления, поэтому работа этих сил за цикл равна нулю. Эти силы считаются внешними силами.

— силы инерции ;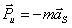

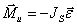
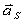
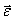
— моменты сил инерции , где m , J_S – масса и массовый момент инерции звена; и – линейное и угловое ускорения;

— силы реакций в кинематических парах 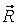, возникающие в опорах звеньев и являющиеся внутренними силами для механизма в целом и внешними для каждого отдельного звена.

Необходимо отметить, что под силами понимаются равнодействующие соответствующих распределенных в месте контакта кинематической пары нагрузок. Все вышесказанное относительно сил распространяется и на моменты сил.

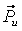
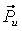
Силы инерции звеньев и моменты сил инерции. Так как звенья механизма находятся в движении, и имеют свои массы, то, особенно в быстродействующих механизмах рычажного типа, обязательно имеет место неравномерность движения звеньев. Это означает, что ускорения этих звеньев не равны нулю, что приводит к возникновению дополнительных сил динамического характера в виде сил инерции и моментов инерции . Из теоретической механики известно, что все силы инерции звена, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную плоскости движения, могут быть сведены к силе инерции , приложенной в центре масс S звена, и паре сил инерции, момент которых обозначим (рис. 4.1).

Рис. 4.1. Сила инерции звена и момента сил инерции

– главный вектор сил инерции, или сила инерции;

– главный момент сил инерции, или момент сил инерции; m – масса звена;

– массовый момент инерции относительно центра масс;

– ускорение центра масс;

– угловое ускорение звена.

и направлены в стороны, противоположные ускорениям и .

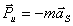
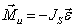
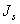
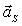
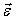
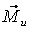
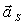
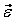
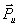
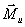
Для дальнейших расчётов удобно заменить и одной силой, использовав для этого 3 метода:

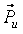
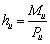
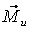
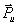
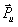
Перенос силы на плечо : момент сил инерции заменяется парой сил с плечом h_u (рис. 4.2), причём одна сила приложена к центру масс звена S и направлена противоположно преобразуемой силе , а другая смещена на плечо h_u и приложена к точке К – центру качания звена.

Рис. 4.2. Перенос силы на плечо при замене силы и момента одной силой

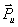
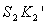
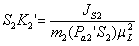
Определение центра качания звена через мгновенный центр ускорений (МЦУ). При этом сила инерции переносится параллельно самой себе на расстояние (рис. 4.3), вычисленное по формуле

, мм ,

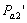
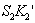
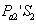
где – мгновенный центр ускорений звена; откладывается в сторону, являющуюся продолжением отрезка .

Рис. 4.3. Определение центра качания звена

Метод замещающих точек. Подробно рассмотрен в литературе.

Рассмотрим определение сил и моментов в различных случаях.

;

; ;

; .

;

; ;

; .

;

; ;

; .

;

; ;

; .

;

; ;

; .

;

; ;

; .

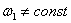
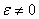
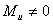
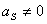
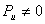
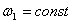
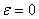
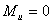
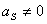
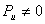
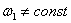
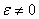
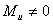
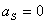
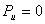
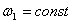
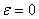
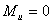
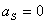
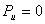
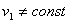
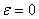
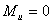
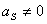
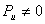
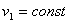
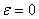
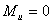
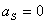
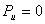
Статическая определимость кинематической цепи

При силовом анализе механизмов (определении неизвестных сил, действующих на движущиеся звенья) можно использовать уравнения (законы) статики. Докажем это положение, проанализировав реакции в кинематических парах (табл.).

Метод кинетостатики. Сила инерции. Принцип Даламбера

Принцип Даламбера.
Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера.

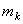
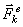
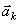
Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой . Под действием приложенных к ней внешних и внутренних сил и (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение .

Введем в рассмотрение величину

,

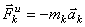
имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции).

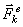
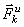
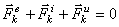
Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам и прибавить силу инерции , то полученная система сил будет уравновешенной, т.е. будет

.

Это выражение выражает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает 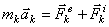. Перенося здесь член в правую часть равенства и придем к последнему соотношению.

Повторяя проделанные высшее рассуждения по отношению к каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики.

Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Кроме того, в соединении с принципом возможных перемещений, который будет рассмотрен в следующей главе, принцип Даламбера позволяет получить новый общий метод решения задач динамики.

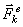
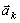
Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы и , возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями . Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции — это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.

Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систе6му. Тогда на основании принципа Даламбера должно быть:

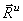
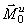
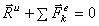
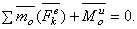
Величины и представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:

, (1)

Применение уравнений (1), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил.

В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.

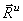
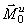
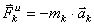
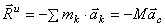
Система сил инерции твёрдого тела можно заменить одной силой, равной и приложенной в центре О, и парой с моментом, равным . Главный вектор системы сил, как известно, не зависит от центра приведения и может быть вычислен заранее. Т.к. , то

(2)

Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

Прикладывается главный вектор к точке приведения, которую можно назначить в любом месте, т.е. он не зависит от выбора этой точки.

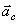
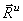
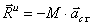
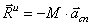
Если ускорение разложить на касательное и нормальное, то вектор разложиться на составляющие

, .

С определением главного момента сил инерции возникает немало сложностей. Рассмотрим несколько частных случаев.

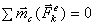
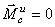
1. Поступательное движение. В этом случае тело никакого вращения вокруг центра масс С не имеет. Отсюда заключаем, что , и равенство (1) даёт .

Следовательно, при поступательном движении силы инерции твёрдого тела приводят к одной равнодействующей, равной 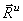и проходящей через центр масс тела.

2. Плоскопараллельное движение. Пусть тело имеет плоскость симметрии и движется параллельно ей. Вследствие симметрии главный вектор и результирующая пара сил инерции, так же как и центр масс С тела, лежат в плоскости симметрии.

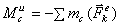
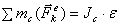
Тогда, помещая центр приведения в точке С, получим из равенства (1) . С другой стороны . Отсюда заключаем, что

Рис.54

(3)

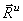
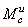
Таким образом, в рассмотренном случае движение системы сил инерции приводится к результирующей силе, равной [формула (2)] и приложенной в центре масс С тела (рис.54), и к лежащей в плоскости симметрии тела паре, момент которой определяется формулой (3). Знак минус в формуле показывает, что направление момента противоположно направлению углового ускорения тела.

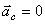
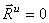
3. Вращение вокруг оси, проходящей через центр масс тела. Пусть опять тело имеет плоскость симметрии, а ось вращения СZ перпендикулярна к этой плоскости и проходит через центр масс тела. Тогда данный случай будет частным случаем предыдущего. Но при этом , а следовательно, и .

Таким образом, в рассмотренном случае система сил инерции приводится к данной паре, лежащей в плоскости, перпендикулярной к оси вращения тела, и имеющей момент

.

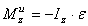
При решение задач по формулам (1) и (3) вычисляются модули соответствующих величин, а направление их указывают на чертеже.

Запишем дифференциальное уравнение движения несвободной материальной точки в виде ma = F + R, где F и R — равнодействующие активных сил и реакций связей, действующих на несвободную материальную точку.

Перенесем член ma в правую часть уравнения и введем в рассмотрение вектор

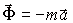(1)

равный произведению массы точки на величину ее ускорения, направленный противоположно вектору ускорения, и назовем введенный вектор даламберовой или просто силой инерции. Тогда основное уравнение динамики несвободной материальной точки примет вид

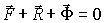(2)

Силы F, R, Ф образуют систему сходящихся сил, а полученное уравнение выражает условие равновесия данной системы сил, что и составляет принцип Даламбера для материальной точки:в каждый момент движения материальной точки активные силы, реакции связей и сила инерции образуют уравновешенную систему сил.

Ускорение точки можно разложить на составляющие. Поэтому и сила инерции раскладывается на соответствующие составляющие, например, в естественной системе координат Ф = Ф_τ + Ф_n, где составляющие силы инерции определяются так: Ф_τ = -ma_τ; Ф_n = -ma_n.

Даламберову силу инерции, введенную по формуле (1), не следует смешивать с реальными физическими силами. Даламберова сила инерции не имеет источника своего возникновения — другого тела. Она вводится условно в ходе математических преобразований основного уравнения динамики, чтобы придать уравнениям динамики вид условия или уравнения равновесия.

Следовательно, прикладывая силу инерции к движущейся материальной точке, мы можем говорить лишь об условном равновесии, приложенных к ней сил. Однако такое понимание динамического уравнения движения позволяет, используя уравнения равновесия статики, составлять динамические уравнения. Этот метод составления уравнений движения и называетсяметодом кинетостатики.

Например, спроектировав (2) на оси прямоугольной системы координат, можно получить три уравнения кинетостатики для материальной точки:

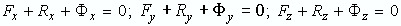(3)

которые представляют собой уравнения равновесия системы сходящихся сил, где к активным силам и реакциям связей, действующим на материальную точку, условно добавлена ее сила инерции. Так как принцип справедлив для любого мгновения времени, оси координат могут быть инерциальными или неинерциальными, неподвижными или подвижными. Важно лишь то, чтобы ускорение точки было определено в инерциальной системе координат или в абсолютном движении.