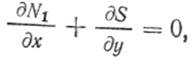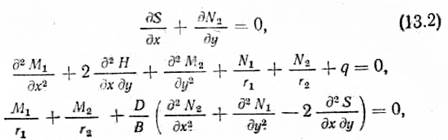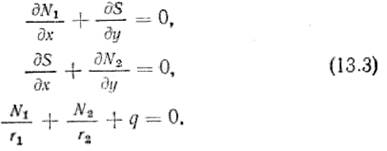Уравнения классической теории тонких упругих оболочек

Основные уравнения теории тонких оболочек

Оболочки весьма распространены в технике, и теоретические основы их расчета к настоящему времени разработаны достаточно глубоко. Предложенные теории, как правило, применимы к оболочкам из идеальных материалов: упругого, упругопластического, упруговязкого. Железобетон не является идеальным материалом, для него характерна нелинейная диаграмма деформирования, при появлении трещин в отдельных зонах оболочек происходит изменение жесткости и перераспределение усилий. Поэтому для установления условий применимости той или иной теории и ее корректировки применительно к данному типу тонкостенных пространственных покрытий проводят эксперименты на моделях или натурных конструкциях.

В качестве основы для расчета большинства применяемых в практике строительства оболочек покрытий принята техническая теория расчета тонких оболочек [19], согласно которой материал оболочки рассматривается как упругий, и считается справедливой гипотеза прямых нормалей: прямолинейный элемент, перпендикулярный срединной поверхности до деформации, остается прямым и перпендикулярным деформированной срединной поверхности и не изменяет своей длины; при этом нормальные напряжения на площадках, параллельных срединной поверхности, считаются пренебрежимо малыми по сравнению с прочими напряжениями.

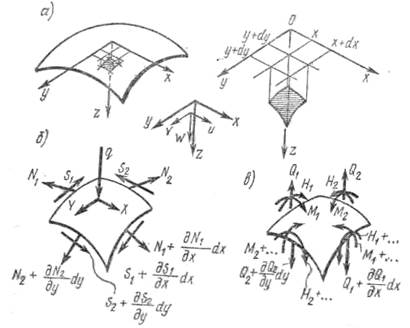
Выделим из оболочки двумя сечениями, параллельными осям х и у, бесконечно малый элемент (рис. 13.3, а). При действии внешней нагрузки на оболочку в элементе возникнут нормальные N₁, N₂, сдвигающие S₁, S₂ силы (рис. 13.3, б), а также изгибающие М₁ и М₂, крутящие H₁ и H₂ моменты и поперечные силы Q₁ и Q₂ (рис. 13.3, в). В пологих тонких оболочках можно принять: S₁=—S₂=S; H₁=-H₂=H. Составляя уравнения равновесия всех действующих на элемент сил и учитывая геометрические и физические соотношения, а также выражая Q₁ и Q₂ через изгибающие и крутящие моменты, можно получить разрешающую систему уравнений [21]:

Рис. 13.3. Усилия, действующие в тонкой оболочке

где D — цилиндрическая жесткость, для железобетонной оболочки D=E_bh 3 /12; q=g+v; B=E_bh.

Из решения (13.2) могут быть найдены искомые внутренние усилия, по которым производится подбор сечений. Приняв в системе (13.2) r₁ = r₂ = ∞, N₁=N₂=S=0, можно получить уравнение изгиба плоской пластинки. Это свидетельствует о том, что нормальные и сдвигающие силы обусловлены именно кривизной оболочки.

Однако решение даже этой упрощенной системы (13.2) при заданных условиях на контуре представляет значительные математические трудности. Для получения более удобных для практических расчетов зависимостей анализируют влияние различных условий на усилия, возникающие в оболочке. В инженерной практике встречаются задачи, когда изгибающие и крутящие моменты в оболочке настолько малы, что ими можно пренебречь. Напряженное состояние в этом случае будет определяться главным образом нормальными и сдвигающими усилиями. Такое «безмоментное» состояние имеет место при соблюдении следующих основных условий: 1) оболочка должна быть тонкой, иметь плавно изменяющуюся поверхность (без переломов и скачкообразного изменения толщины); 2) нагрузка на оболочку должна изменяться плавно и быть непрерывной; 3) условия закрепления краев оболочки должны обеспечивать свободные их перемещения в направлении нормали к поверхности.

При выполнении этих условий в системе (13.2) можно принять D = 0 и M₁=M₂=H=0, тогда расчетные усилия безмоментного состояния оболочки определяют из уравнений:

Решения этой системы разработаны достаточно подробно для широкого класса задач. При невыполнении сформулированных выше условий необходимо исходить из общей системы (13.2).

На базе технической теории и результатов экспериментов разработаны практические (инженерные) методы расчета различных тонкостенных пространственных покрытий, изложенные в последующих параграфах. Однако техническая теория справедлива, если прогибы тонкой оболочки малы по сравнению с ее толщиной. Если же они оказываются соизмеримыми с толщиной оболочки, возникает так называемая геометрическая нелинейность, что может повлиять на значения усилий. Система разрешающих уравнений в этом случае усложняется.

В последние годы интенсивно развиваются более точные методы расчета тонкостенных пространственных покрытий, учитывающие геометрическую и физическую нелинейность, наличие трещин и перераспределение усилий, характер армирования, предварительное напряжение и т. п. В их основе лежат численные методы (конечного элемента, конечных разностей), которые реализуются на ЭВМ. Вместе с тем методы, базирующиеся на технической теории, не утрачивают своего значения. Они широко применяются для предварительного подбора сечений элементов оболочек и их армирования, при вариантном проектировании, а также используются при анализе решений, получаемых с помощью ЭВМ.

Для определения полной несущей способности оболочек при действии распределенных и сосредоточенных нагрузок используется метод предельного равновесия (см. гл. 9).

Теория оболочек

Введение. Основные определения

Конструктивные формы современных машин и сооружений чрезвычайно разнообразны. Выбор формы детали, узла или сооружения определяется многими факторами: их назначением, условиями работы, технологией изготовления, стоимостью, а также методами расчета. Одним из самых распространенных типов современных и перспективных конструкций являются тонкостенные оболочки. Тонкие пластины и оболочки находят исключительно широкое применение в конструкции самых разнообразных инженерных сооружений. По этой причине создание надежных совершенных конструкций непосредственно зависит от уровня развития теории тонких пластин и оболочек.

Тонкая оболочка может быть определена как тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми мало по сравнению с другими размерами. Таким образом, для оболочечных конструкций характерна тонкостенность .

К оболочкам относятся, в частности, тонкостенные пространственные системы, очерченные по криволинейным поверхностям. Оболочки способны выдерживать разнообразные виды нагрузок и обеспечивать изоляцию от окружающей среды. Им можно придать обтекаемую форму и на их основе получить относительно легкие конструкции, что имеет огромное значение в авиакосмической промышленности

Снижение материалоемкости конструкции — важный фактор для многих машин и агрегатов. Выгодно это и в строительных сооружениях. Оболочки позволяют эффективно решать проблему минимизации массы.

В настоящее время оболочки можно видеть повсюду. Высотные здания и телебашни, спортивно-концертные комплексы, крытые стадионы и рынки, цистерны и резервуары, трубопроводы и градирни, самолеты и ракеты, надводные и подводные корабли, автомобили в существенной части состоят из оболочек. Транспортные конструкции характеризуются не только возможностью достижения высоких скоростей, аэродинамическим совершенством форм, грузоподъемностью. Они воплощают также идеи оптимальности, экономичности, весового совершенства.

Оболочки как элементы конструкций известны давно. Это и паровой котел, и водопровод в древнем Риме. С давних времен известны емкости для хранения жидкостей и зерна, криволинейные своды перекрытий в строительстве. Но решающую роль в самых различных областях современной техники оболочки стали играть последние несколько десятилетий.

Термин «оболочка» относится к числу перегруженных и в него можно вкладывать разный смысл. Далее под оболочками понимаются конструкции, способные выполнять силовые, эксплуатационные, технологические, архитектурные и эстетические функции.

При математическом моделировании с понятием оболочки в первую очередь связывается представление о геометрической поверхности . В механике деформируемого твердого тела и строительной механике классификация объектов (тел) основана на особенностях их формы и соотношении характерных размеров.

Принято различать и выделять элементы конструкций, один размер которых намного больше двух других. Это стержни, кольца, арки. Тела, у которых один размер намного меньше остальных, образуют класс оболочек и пластин.

Основная проблема теории тонких упругих оболочек состоит в сведении трехмерной задачи теории упругости к двумерной задачи. Таким образом, развитие общей теории тонких упругих пластин и оболочек идет по пути сведения трехмерных уравнений теории упругости к двумерным. Для решения этой проблемы предложено большое число методов, которые по классификации С.А. Амбарцумяна могут быть объединены в три группы: метод гипотез, метод разложения общих уравнений теории упругости по толщине оболочки и асимптотический метод. Все эти методы интенсивно развиваются, дополняя друг друга.

Список обозначений

a₁ , a₂ — криволинейные ортогональные координаты срединной поверхности S_o оболочки на линиях главных кривизн; для оболочки вращения a₁ ─ продольная, a₂ -окружная координаты; z ─ координата по нормали к S;

А₁ , А₂ -коэффициенты Лямэ; k₁ , k₂ -главные кривизны;

U, V, W- компоненты вектора перемещений произвольной точки оболочки;

u, v, w- компоненты вектора перемещений точек поверхности S_o ;

q ₁ , q₂ — углы поворота нормали ;

e_jk — компоненты тензора деформаций;

E₁₁ , E₂₂ , E₁₂ — компоненты тангенциальной деформации на S: растяжения-сжатия по направлениям координат a₁ и a₂ и сдвиг;

K₁₁ , K₂₂ , K₁₂ — компоненты изгибной деформации: изменения главных кривизн и кручение;

T₁₁ , T₂₂ , S- тангенциальные внутренние усилия, приведенные к S_o : усилия растяжения-сжатия и сдвига;

M₁₁ , M₂₂ , H- изгибающие и крутящий моменты;

Q₁₁ , Q₂₂ — перерезывающие силы;

q₁ , q₂ , q₃ — компоненты внешней поверхностной нагрузки, приведенные к S;

E, n- модуль Юнга и коэффициенты Пуассона материала оболочки;

y_j -унифицированные обозначения основных независимых переменных в разрешающих системах обыкновенных дифференциальных уравнений (ОДУ);

f_j — операторы правых частей канонических систем ОДУ;

Рассмотрим элемент произвольной тонкой оболочки, пусть в дальнейшем

h- толщина оболочки, принимаемая в дальнейшем постоянной.

Обозначим через R₁ , R₂ — главные радиусы кривизны срединной поверхности оболочки S. R=min 1 , R₂ >.

Основным геометрическим параметром оболочки является параметр тонкостенности или относительная толщина, определяемый отношением e=h/R.

Принята достаточно условная классификация оболочек по ее толщине на тонкие, средней длины и толстые оболочки.

Будем считать оболочку тонкой, если ее относительная толщина значительно меньше единицы. Обычно оболочки считают тонкими при значении e 1/10 — толстой оболочке.

Для незамкнутых оболочек можно задать характерный размер размер a. Тогда параметр тонкостенности можно определить как e = min (h/a, h/R).

Поверхность оболочки S, равноотстоящая от лицевых поверхностей S₊ и S _— называется ее срединной поверхностью.

Криволинейные, ортогональные системы координат

Правило дифференцирования базисных векторов криволинейной ортогональной системы координат определяется следующим образом:

Здесь H_{m —} параметры Ляме координатной системы, имеющие вид

= (r_{, i} ) 2 ; Hi = ½ r_{, i} ½ .

Здесь r_{, I —} радиус — вектор произвольной точки тела оболочки. В частности:

Запишем условие совместности, которое в принятых обозначениях имеет вид:

Тогда, приравнивая коэффициенты при базисных векторах, получим:

e ₂ : (H_2,1 /H₁ ),₁ + (H_1,2 /H₂ ),₂ + (H_1,3 × H_2,3 ) / = 0

Круговая перестановка индексов приводит к шести уравнениям совместности параметров Ляме.

Некоторые сведения из теории поверхностей

Рассмотрим произвольную гладкую поверхность и систему декартовых координат x, y, z.

Пусть r = r (a₁ , a₂ ) — радиус-вектор произвольной точки срединной поверхности оболочки. Рассмотрим производные r по переменным a₁ и a₂

Введем в рассмотрение базис

Составим скалярные произведения:

r _a ×r _b =G_{a b} ; G₁₁ = ; G₂₂ =

G₁₂ = G₂₁ = 0 для ортогональной системы координат

При этом образуется тензор второго ранга = G_{a b} r _a r _b , который называется первым фундаментальным тензором поверхности.

= (r ₁ da₁ + r ₂ da₂ ) 2 = G₁₁ d + 2G₁₂ da₁ da₂ +C₂₂ d =

= d + d;

Коэффициенты А₁ и А₂ являются коэффициентами первой квадратичной формы и называются параметрами Ляме. Первая квадратичная форма определяет так называемую внутреннюю геометрию поверхности и определяет метрику поверхности. Введем в рассмотрение единичный вектор внешней нормали к поверхности N. Запишем очевидное соотношение N ×N =1 и продифференцируем его по a₁ , a₂ :

2N ×N _{, i} = 0; очевидно, вектор N _{, I} лежит в касательной плоскости к поверхности Sи может быть представлен в виде разложения N _{, i} = B_ij r _j.

При этом вводится в рассмотрение тензор второго ранга

= B_{a b} ×r _a ×r _b,

являющийся вторым фундаментальным тензором поверхности, а его компоненты B_{a b —} коэффициентами второй квадратичной формы поверхности, определяющей внешнюю геометрию поверхности.

В главных осях тензор может быть записан в виде:

= = k₁ e ₁ e ₁ + k₂ e ₂ e ₂

В дальнейшем координатные линии выбираются вдоль главных осей кривизны. Пусть в дальнейшем

I₁ = k₁ + k₂ — первый инвариант (средняя кривизна)

I₂ = k₁ ×k₂ — второй инвариант (гауссова кривизна)

Специальная система координат в теории оболочек

Для любой точки тела оболочки:

= (r _{, i} ) 2 = (r _{, i} + (a₃ N ), i) 2 = (r _i + a₃ B_ij r _j ) 2 (B₁₂ = B₂₁ =0)

= (r ₁ + a₃ N _,1 ) 2 = (r₁ + a₃ × B₁₁ r ₁ ) 2 = (1 + a₃ k₁ ) 2

= N ×N = 1 ®H₃ = 1 –

параметры Ляме в специальной системе координат

Соотношения Гаусса и Кодацци

Уравнения совместности параметров Ляме:

(H_2,1 /H₁ ),₁ + (H_1,2 /H₂ ),₂ + (H_1,3 × H_2,3 ) / = 0

В специальной системе координат

Рассмотрим срединную поверхность a₃ = 0

при замене индексов получаем два соотношения Кодацци

R — текущая конфигурация

r — отсчетная конфигурация

Дифференцирование ортов в специальной системе координат

Удлинения, сдвиги и повороты элемента сплошной среды

а) Рассмотрим удлинения

dr — в отсчетной конфигурации, dR — в текущей конфигурации

dR = dr × ; R ( = e _k (…),_k / H_k )

(r + u ) = r + u = u

Рассмотрим относительное удлинение

dS 2 — ds 2 = dR × dR — dr × dr = dr × × dr × — dr × dr =

=dr × × × dr — dr × × dr = dr ( × — × ) × dr =

= 2dr × × dr ; = 0,5 ( × — ) — тензор деформаций Грина

= 0,5 [ ( + u ) ( + u T ) — ] = 0,5 ( u + u T + u × u T )

dS 2 — ds 2 = 2ds 2 e ×e G ×e

( dS 2 — ds 2 ) /ds 2 = (dS/ds) 2 — 1 = 2e ×e G ×e

dS/ds = (1 + 2e ×e G ×e ) 1/2 ;

e_e = (dS — ds) /ds = (1 + 2e ×e G ×e ) 1/2 — 1 — удлинение

Пусть e = e ₁ ; = (1+2 ) 1/2 — 1 = 1 + + … — 1 = »e ₁₁

e = 0,5 (Ñu +Ñu T ) — линейный тензор деформаций Коши.

Деформации сдвига

Выделим два прямолинейных волокна, направление которых определяется единичными векторами m ₁ и m ₂

ds_i = ½dr _i ½- длины элементов волокон до деформаций

Деформации сдвига характеризуется изменением угла q₁₂

= m ₁ ×m ₂ — [ (dr ₁ × × dr ₂ ) / ds₁ (1+e_m1 ) ds₂ (1+e_m2 )] =

= m ₁ ×m ₂ — m ₁ × ×m ₂ = m ₁ × ( — ) ×m ₂ = — 2m ₁ × ×m ₂ ;

cos q₁₂ = 0 0 — cos Q₁₂ = -2

cos Q₁₂ = cos (p/2 — g₁₂ ) = 2 = sin g₁₂ = g₁₂

Повороты

Рассмотрим материальное волокно dr = e ds

w = (dr ´dR ) / (½dr ½×½dR ½) — вектор поворота материального волокна

w — нормаль, относительно которой происходит поворот

w = (dr ´ (dr × )) / (ds ×ds (1 + e_e )) = e ´ (e × ) =

= e ´ [e × ( u )] = e ´e + e ´ (e × u ) = e ´ (e × u )

Пусть e = e _t — базисные вектора t = 1,2,3

w _t — вектор поворота материального волокна t

w _t = e _t ´ (e _t × u ) = e _t ´ (e _t × u_kj e _k e _j ) =

u = u_kj e _k e _j = e _t ´ (u_kj d_tk e _j ) = e _t ´ u_tj e _j =

‘_tjk — символы Леви-Чивита, которые определяются:

СЛЧ = 0, если среди r,s,t есть одинаковые

=+1, если индексы r,s,t — различные ® 123, 231, 312

= -1, если этот порядок нарушается

w _tk характеризует поворот орта tотносительно орта k.

Введем тензор второго ранга = w_tk e _t e _k — тензор поворота

Определим компоненты градиента вектора перемещений в специальной системе координат:

( = e _{s (} …),_s / H_s ; H_i = A_{i (} 1 + a₃ k_i ) i = 1,2 H₃ = 1

“o” — в дальнейшем опускаем

После подстановки выражений e_{k , j} (j,k = 1,2,3)

h/2 £a₃ £h/2; учитывая, что h/R_i » 1, т.е. оболочка тонкая, получим:

= 0,5 (Ñu + Ñu T ) Þ e_ii = u_ii

Для удлинений имеем:

Для деформаций сдвига соответственно:

Углы поворота определяются через перемещения следующим образом: w_ii = 0

Теория малых удлинений и малых квадратов углов поворота

Рассмотрим тензор нелинейных деформаций Грина:

= 0,5 (Ñu + Ñu T + Ñu ×Ñu T ) = + 0,5Ñu ×Ñu T

Его нелинейная часть определяется следующим образом:

Таким образом, компоненты тензора деформаций можно записать в виде:

e₁₁ = e₁₁ + 0,5 ( )

e₂₂ = e₂₂ + 0,5 ( )

e₃₃ = e₃₃ + 0,5 ( )

или, подставляя выражения для углов поворота:

e₁₁ = e₁₁ + 0,5 ( )

e₂₂ = e₂₂ + 0,5 ( )

e₃₃ = e₃₃ + 0,5 ( )

Введем следующие предположения:

u °- вектор перемещений точек, лежащих на S

В координатной форме соответственно:

u₁ = (a₁ , a₂ ) + a₃ (a₁ , a₂ )

u₂ = (a₁ , a₂ ) + a₃ (a₁ , a₂ )

u₃ = (a₁ , a₂ )

При этом компоненты вектора перемещений u₁ и u₂ линейным образом зависят от координаты a_3, а функция поперечногопрогиба постоянна по толщине в силу недеформируемости нормали.

Рассмотрим детальнее геометрическую гипотезу Кирхгоффа-Лява. Тот факт, что нормаль к срединной поверхности S в процессе деформирования остается нормалью приводит к соотношениям:

/A₁ + — ( + a₃ ) k₁ = 0

(1 — a₃ k₁ ) — k₁ + /A₁ = 0