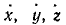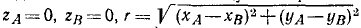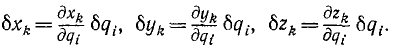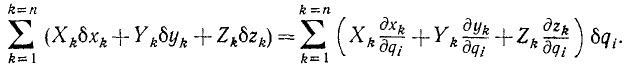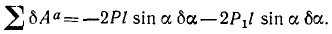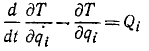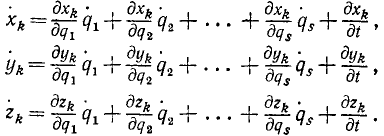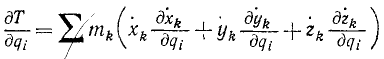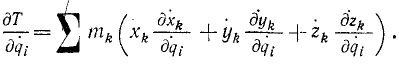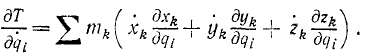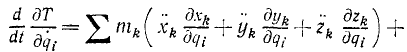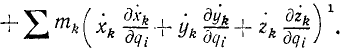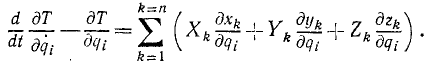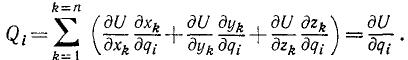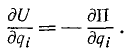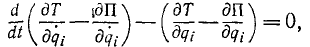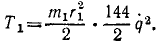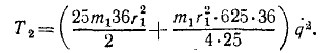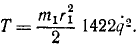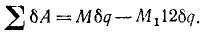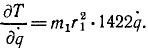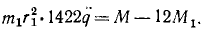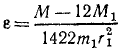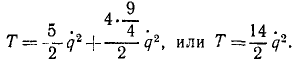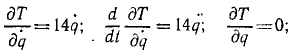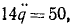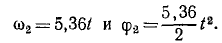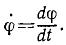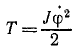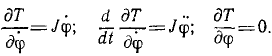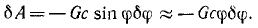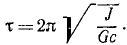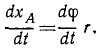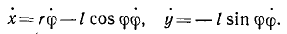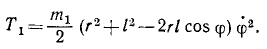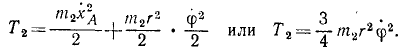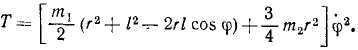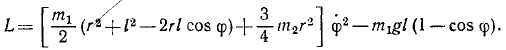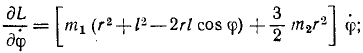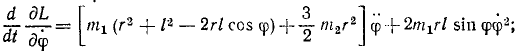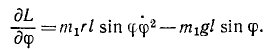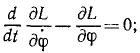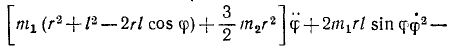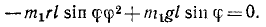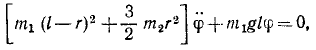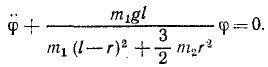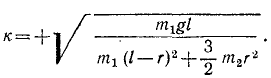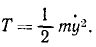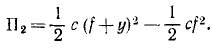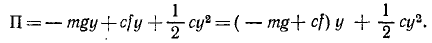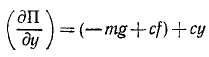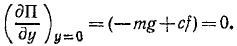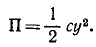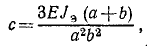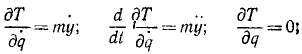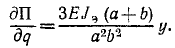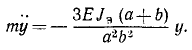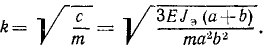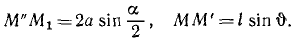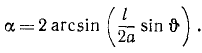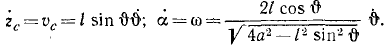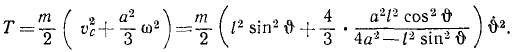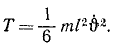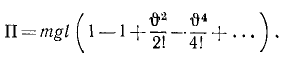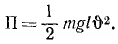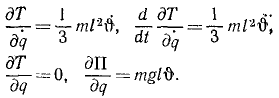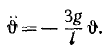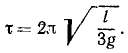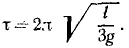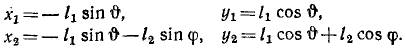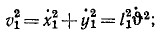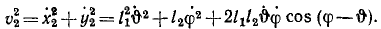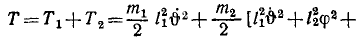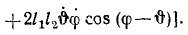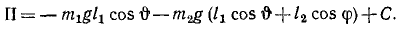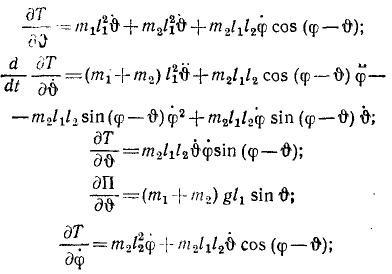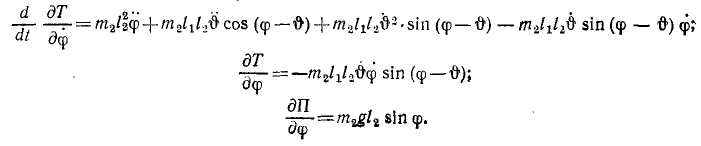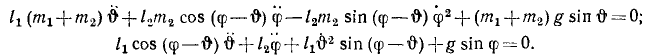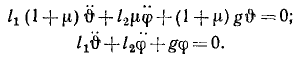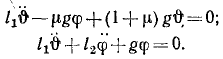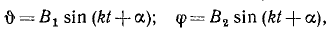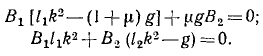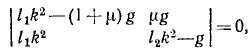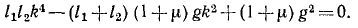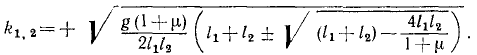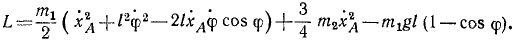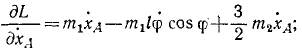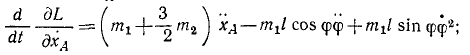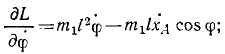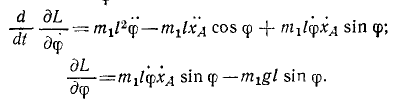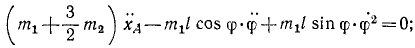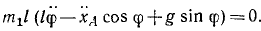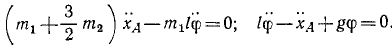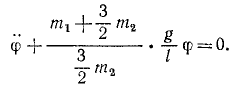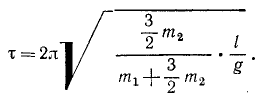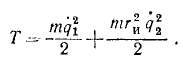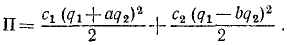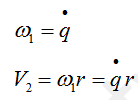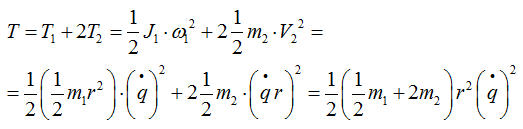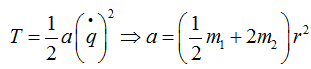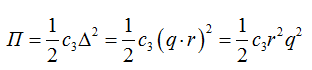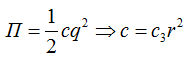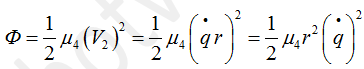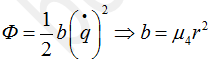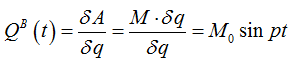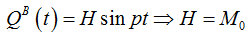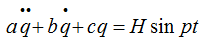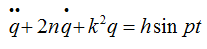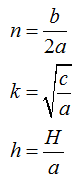Уравнения колебаний в обобщенных координатах

Обобщенные координаты системы в теоретической механике

Содержание:

Обобщенные координаты системы:

Голономными называют свя­зи, налагающие ограничения только на положение точек системы и, следовательно, выражающиеся конечными соотношениями между коор­динатами этих точек

Голономные связи

Связи, с которыми мы встречались при решении задач по статике, ограничивали свободу перемещения тел и не зависели от времени. Мы назвали связью ограничения, стесняющие движение материальной точки или ме­ханической системы, осуществляемые дру­гими материальными объектами. Под это определение подходят также и такие связи, которые ограничивают не только перемещения, но и скорости точек механической системы. Рассмотрим следующий пример.

Пример. 1-й случай.

Шар радиуса к может передвигаться (скользить и перекатываться по плоскости xOy); 2-й случай: шар может только перекатываться без скольжения по плоскости. В первом случае связь может быть выражена уравнением z_с=r, которое не содержит производных от координат по времени и накладывает ограничение только на положение точки C (центра шара). Во втором случае на шар наложена связь, заключающаяся в том, что скорость точки касания равна пулю, а следовательно, уравнение связи должно выражать условие, чтобы равнялись нулю производные по времени

В первом случае движение шара подчинено голономной связи, а во втором — неголономной. Вообще, голономными, или конечными, связями называют связи, накладывающие ограничения только на положение материальных точек системы. Они выражаются аналитически конечными соотношениями между координатами точек системы, причем в эти соотношения может явно входить и время. Обратим внимание на тот факт, что, продифференцировав по времени такое уравнение, мы получим уравнение связи, содержащее явно проекции скоростей точек. Но это уравнение явится лишь следствием того уравнения, из которого оно было получено путем дифференцирования. Оно будет автоматически выполняться при удовлетворении голономной связи.

Следовательно, если уравнение связи содержит проекции скоростей точек, то отсюда еще не следует делать вывод, что связь не является голономной. Нужно предварительно исследовать, возможно ли проинтегрировать это уравнение и получить из него уравнение, не содержащее проекций скоростей точек. Если это можно, то связь является голономной, в противном случае связь называют неголономной, или неинтегрируемой. Если среди связей, наложенных на систему, имеется хоть одна неголономная связь, то систему называют неголономной. В дальнейшем мы будем рассматривать лишь голономные системы.

Обобщенными координатами системы называют независимые друг от друга величины, вполне и однозначно определяющие возможные положения системы в произвольно выбранное мгновение

Обобщенные координаты

Положение в пространстве свободной материальной точки определяется тремя координатами, независимыми друг от друга. Такая точка имеет три степени свободы. Для определения положения в мгновение t системы, состоящей из n свободных точек, необходимо 3 n координат. Если система не свободна, то связи, наложенные на систему, выражают некоторые зависимости между координатами ее точек, а поэтому число независимых друг от друга координат, определяющих положение в данное мгновение всех точек несвободной системы, меньше чем 3 n.

Пример:

Система состоит из двух точек А и В. Согласно связям, наложенным на эти точки другими материальными телами, точки А и В могут двигаться только в плоскости хОу и находиться на постоянном между собой расстоянии r. Связи голономные них уравнения

Из этого примера видно, что вместо декартовых координат за независимые можно выбирать другие, связанные с ними величины, даже и другой размерности (угол). Эти независимые параметры называют обобщенными координатами системы и обозначают буквой q. Так, в рассмотренном примере мы могли выбрать следующие обобщенные координаты: 1) q₁ = x_A, q₂ = y_A, q₃=x_B или 2) q₁ =х_B, q₂ = у_B, q₃=φ. Возможен, разумеется, и другой выбор трех обобщенных координат этой механической системы.

Следовательно, под обобщенными координатами системы мы понимаем независимые друг от друга величины, обычно имеющие размерность длины [q] =L 1 M 0 T 0 или угла [q] = L 0 M 0 T 0 и определяющие полностью и однозначно возможные положения системы в данное произвольно выбранное мгновение. Но встречаются случаи, когда обобщенные координаты имеют размерность площади или объема, или других геометрических или даже механических величин.

Декартовы координаты точек системы связаны с обобщенными координатами определенными уравнениями. Они являются функциями обобщенных координат и, возможно, времени. Так, если положение системы n точек определяется s обобщенными координатами (q_l, q₂, . q,), то эти уравнения в параметрической форме имеют вид:

(258)

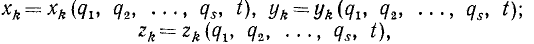
Число степеней свободы голономной механической системы равно числу обобщенных координат

Если на систему наложены только голономные связи, то число обобщенных координат системы равно числу ее степеней свободы. Заметим, что к неголономным системам это правило не относится. В прикладной механике большое значение имеют полносвязные системы, т. е. механические системы с одной степенью свободы. К числу таких систем относится большинство механизмов. Чтобы определить положение полносвязной системы, достаточно одной обобщенной координаты.

Примеры:

Тело с двумя неподвижными точками имеет одну степень свободы: оно может поворачиваться вокруг неподвижной оси, проходящей через эти закрепленные точки. Для определения положения тела, занимаемого им в данное мгновение, нужна лишь одна обобщенная координата, например угол поворота φ.

Тело с одной неподвижной точкой имеет три степени свободы и его положение определяют тремя обобщенными координатами, например тремя углами Эйлера.

Кривошипно-ползунный механизм (рис. 238)—система с одной степенью свободы. Чтобы задать положение всех точек механизма, нет надобности задавать декартовы координаты всех точек, достаточно одной обобщенной координаты, например угла φ или дуги A₀A. Одной обобщенной координатой и уравнениями связи 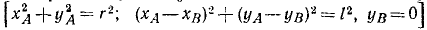положение механизма, занимаемое им в данное мгновение, определяется вполне и однозначно.

Регулятор Уатта имеет две степени свободы и для определения его положения нужно задать две независимые друг от друга величины, т. е. две обобщенные координаты, например угол (см. рис. 236) отклонения ручек от вертикали и угол поворота плоскости AOB вокруг оси Оу.

Обобщенные координаты, как и всякие координаты, характеризуют положение неподвижной системы или положение движущейся системы, занимаемое ею в данное мгновение. Чтобы охарактеризовать движение системы, надо выразить обобщенные координаты как непрерывные однозначные функции времени. Изменение каждой обобщенной координаты характеризует соответствующее изменение в положении системы. Так, в последнем из разобранных примеров (регулятор Уатта) изменение одной обобщенной координаты означает поворот системы вокруг вертикальной оси, а изменение другой обобщенной координаты выражает изменение наклона ручек к вертикальной оси.

Обобщенная скорость выражается первой производной от обобщенной координаты по времени

Обобщенная скорость

Для характеристики движения системы, определяемого обобщенной координатой q_i=q_l(t) не только в пространстве, но и во времени, возьмем первую производную от этой координаты по времени
(259)

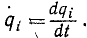
Полученная величина является пространственно-временной характеристикой изменения одной из обобщенных координат. Ее называют обобщенной скоростью, соответствующей данной координате. Каждой обобщенной координате соответствует своя обобщенная скорость, поэтому число обобщенных скоростей в системе равно числу обобщенных координат.

Обобщенная координата обычно выражается длиной или углом, соответственно этому обобщенная скорость может иметь размерность либо скорости точки, либо угловой скорости тела.

Обобщенной силой называют скалярную величину, равную отношению суммы виртуальных работ всех сил системы при изменении только одной из обобщенных координат к вариации этой координаты

Обобщенная сила

Пусть положение механической системы в данное мгновение t определяется обобщенными координатами q₁, q₂, . q_s. Дадим одной из координат qi мысленно бесконечно малое изменение δqi, сохранив для всех остальных обобщенных координат то значение, которое они в данное мгновение имеют. Вследствие изменения одной из обобщенных координат материальные точки системы получат мысленные бесконечно малые перемещения, а приложенные к этим точкам силы произведут виртуальную работу:

(221)

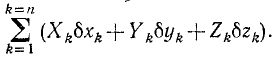
Сумма работ всех реакций на данном виртуальном перемещении равна нулю (так как связи предполагаем идеальными), поэтому написанная сумма выражает работу всех активных сил системы. Из уравнений (258) найдем вариации декартовых координат точек системы, соответствующих приращению δq_i обобщенной координаты q_i при фиксированном (неизменном) значении других обобщенных координат:

Эти вариации подставим в предыдущее выражение:

Эту сумму виртуальных работ всех сил (или, что то же, всех активных сил), приложенных к системе, при изменении только одной из обобщенных координат q_i мы можем записать как произведение вариации bqi этой координаты на скалярную величину

(260)

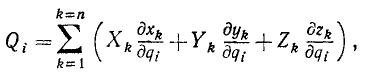
называемую обобщенной силой, соответствующей координате q_i.

Если мы дадим воображаемое приращение какой-либо другой из обобщенных координат этой системы при фиксированном значении всех остальных обобщенных координат, то совершенно аналогично получим выражение обобщенной силы, соответствующей этой второй обобщенной координате. Таким образом, в системе столько же обобщенных сил, сколько в ней обобщенных координат.

Размерность обобщенной силы равна размерности работы, поделенной на размерность обобщенной координаты, а эта последняя обычно имеет размерность длины или угла. Следовательно, обобщенная сила может иметь размерность силы или же размерность момента силы в зависимости от размерности соответствующей обобщенной координаты.

Задача №1

Определить обобщенную силу в регуляторе Уатта (рис. 236 на стр. 424), соответствующую обобщенной координате а. Точечные грузы А и В имеют одинаковый вес P кГ, вес муфты C равен P₁ кГ, а стержни имеют одинаковую длину 1 мм.

Решение. Декартовы координаты точек приложения силы, как функции обобщенной координаты (параметра а), их вариации и виртуальные работы всех активных и инерционных сил определены при решении задачи № 188. Для вычисления обобщенной силы воспользуемся некоторыми полученными при решении задачи № 188 данными и составим сумму виртуальных работ только активных сил при вариации δα:

Разделив эту сумму виртуальных работ активных сил системы на δα, получим ответ.
Ответ. Q = —2l (P + P₁) sin α kΓ∙ мм.

Разность производной по времени от обобщенного импульса и частной производной от кинетической энергии системы по обобщенной координате равна обобщенной силе:

Уравнения Лагранжа в обобщенных координатах

Выразим в обобщенных координатах проекции скоростей точек системы на оси декартовых координат. Для этого продифференцируем по времени соотношения (258). Имеем:

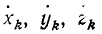
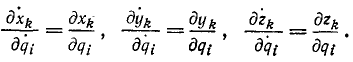
Возьмем теперь частные производные этих проекций скоростей по какой-либо одной обобщенной скорости q_i:

(261)

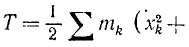
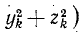
Эти соотношения справедливы только для голономных систем, и мы воспользуемся ими для вывода дифференциальных уравнений движения таких систем в обобщенных координатах. Возьмем частные производные от (215′) кинетической энергии системы по обобщенной координате q_i и по обобщенной скорости q_i:

Производную от кинетической энергии по обобщенной скорости называемую обобщенным импульсом, мы представим в другом виде, для чего воспользуемся соотношениями (261):

Продифференцируем обобщенный импульс по времени:

Преобразуем первую сумму правой части этого равенства, приняв во внимание дифференциальные уравнения движения системы в форме (130): m_kx_{k =} X_k, m_ky_k = Y_k, m_kz_k = Z_k, вторую сумму, равную 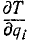, перенесем влево:

В правой части имеем обобщенную силу системы, соответствующую координате q_i. Обозначая, согласно (260), правую часть этого равенства через Q_i, мы получим уравнения движения материальной системы в обобщенных координатах, называемые иначе уравнениями (второго рода) Лагранжа:

(262)

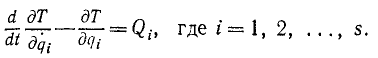
Случай существования силовой функции

Если к механической системе приложены только силы поля и существует силовая функция U, то, имея в виду равенства (238),

Или, так как U =— П, где П — потенциальная энергия (244),

Подставляя в уравнения Лагранжа вместо обобщенной силы Q ее выражение через потенциальную энергию, получим удобную форму уравнений Лагранжа для случая консервативной системы:

(263)

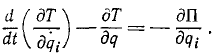
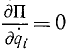
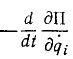
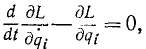
Иногда этому выражению придают еще более простой вид, пользуясь тем, что потенциальная энергия П не зависит от обобщенных скоростей и потому ; перенеся все члены в левую часть и прибавив , получим

(264)

называют функцией Лагранжа.

Задача №2

В планетарном механизме изображенном на рис. 146, а, определить угловое ускорение колеса l при следующих условиях.

Передаточное число 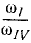= 12. К колесу l приложен постоянный момент сопротивления M₁, а к рукоятке IV—постоянный вращающий момент М. Колеса l и 1 l считать однородными дисками одинаковой толщины и из одного и того же материала. Массой рукоятки IV пренебречь. Механизм находится в горизонтальной плоскости.

Решение. Механизм имеет одну степень свободы, следовательно, его положение можно определить одной обобщенной координатой, а его движение—одним уравнением Лагранжа. В данном случае за обобщенную координату удобно выбрать угол φ₄ поворота рукоятки (φ₄ = q). Тогда обобщенная скорость системы равна угловой скорости рукоятки (q = ω₄). Выразим в обобщенной скорости кинетическую энергию системы, которая равна сумме кинетических энергий первого и второго колес.

Момент инерции первого колеса 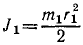, его угловая скорость ω₁= 12q и

Радиус второго колеса (см. задачу № 90) r₂ = 5r₁, следовательно, масса второго колеса в 25 раз больше массы первого, а его момент инерции в 625 раз больше. Скорость его центра равна q∙6r₁, а его угловая скорость 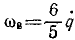. Его кинетическую энергию определяем по формуле Кёнига:

Кинетическая энергия механизма

Чтобы подсчитать обобщенную силу, определим работу всех активных сил системы при вариации обобщенной координаты. Сообщим координате малое приращение δq, т. е. мысленно повернем рукоятку на угол δq₄. Тогда первое колесо повернется на угол 12δq и произойдет работа

Эта работа равна работе Qδq обобщенной силы, следовательно, обобщенная сила в этой задаче имеет размерность момента силы и равна

Составим уравнение Лагранжа (262). Частная производная от кинетической энергии системы по обобщенной скорости

После дифференцирования по времени q заменится ‘q. Частная производная от кинетической энергии по обобщенной координате равна нулю. Следовательно,

Из этого уравнения непосредственно определяем ускорение ε = q рукоятки механизма при заданных моментах.

Ответ.

Задача №3

Решить задачу уравнением Лагранжа.

Решение. В этой задаче будем выражать L в м, T в сек, F в кГ. Система имеет одну степень свободы. За обобщенную координату q выберем угол поворота φ1 первого вала. Тогда обобщенной скоростью q системы будет угловая скорость первого вала. Угловая скорость второго вала равна 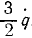. Кинетическая энергия системы

Вычислим величины, входящие в уравнение Лагранжа (262):

Напишем уравнение движения системы:

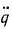
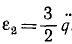
откуда =3,57 ceκ -2 и по передаточному отношению , т. е. ε₂ = 5,36 ceκ -2 . Вращение равноускоренное, без начальной угловой скорости, следовательно, по (87):

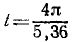
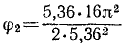
Угловая скорость будет 120 об/мин, т. е. 4π сек -1 , откуда ; в мгновение второй вал будет повернут на угол . Чтобы определить соответствующее число оборотов вала, надо разделить угол поворота на 2л.
Ответ. Через 2,344 оборота.

Малые колебания системы

Движение, при котором точки системы перемещаются последовательно в ту и в другую сторону от некоторых средних своих положений, называют колебательным.

Во многих областях техники часто приходится рассматривать колебательные движения механических систем, т. е. такие движения, при которых точки системы перемещаются последовательно то в ту, то в другую сторону относительно их некоторого среднего положения. Сюда относят вибрации машин и их деталей, возникающие при различных условиях, вибрации инженерных сооружений и их отдельных элементов, а также автомобилей, судов, самолетов и пр.

Колебательные движения механических систем удобно описывать уравнениями Лагранжа в обобщенных координатах. При составлении уравнений мы будем отсчитывать обобщенные координаты всегда от положения устойчивого равновесия, относительно которого и происходят колебания механических систем. В большинстве случаев эти уравнения нелинейны и их интегрирование связано с большими трудностями. Однако при решении многих технических задач оказывается возможным в этих уравнениях отбрасывать квадраты и более высокие степени координат и скоростей. Такая операция называется линеаризацией уравнений. Линеаризованные уравнения не могут, конечно, в точности отобразить движения системы и дают несколько искаженную картину явления. Искажения тем менее существенны, чем меньше отброшенные члены уравнений в сравнении с оставшимися. Если значения координат и скоростей во все время движения остаются очень малыми, то их квадратами и высшими степенями вполне можно пренебречь, подобно тому, как в дифференциальном исчислении пренебрегают бесконечно малыми высших порядков. Таким образом, мы пришли к заключению, что колебания, описываемые линеаризованными уравнениями при сделанном выборе начала отсчета, должны быть только малыми колебаниями около положения равновесия.

Колеблющиеся механические системы обычно являются консервативными, т. е. их колебания происходят в потенциальном поле, поэтому уравнения Лагранжа удобно писать в форме (263) и (264). Напомним, что в выражение потенциальной энергии входит произвольная постоянная С, несущественная для расчетов, так как в расчетах мы всегда встречаем не полную потенциальную энергию, а ее изменение. Но все же мы будем стараться так определить эту постоянную, чтобы потенциальная энергия системы при равновесном положении, т. е. при равенстве нулю обобщенных координат, тоже равнялась нулю. Тогда при отклонении системы от равновесного положения потенциальная энергия получается положительной, потому что равновесие йвляется устойчивым, а потенциальная энергия в этом положении (П = 0) согласно теореме Лежен Дирихле должна иметь минимум.

Рассмотрим несколько задач на малые колебания системы, причем для начала рассмотрим с позиций уравнений Лагранжа малые колебания физического маятника.

Задача №4

Определить малые колебания физического маятника без сопротивления на неподвижной оси (см. рис. 192 на стр. 334). Все данные по геометрии масс маятника считать заданными.

Решение. Задачу будем решать по (262). Направим оси декартовых координат как указано на чертеже (рис. 192). За обобщенную координату примем угол φ отклонения маятника от вертикали, т. е. будем отсчитывать обобщенную координату φ от положения устойчивого равновесия системы. Тогда обобщенная скорость (259)

Выразим кинетическую энергию через обобщенную координату

и вычислим производные, входящие в левую часть уравнения (262):

Для определения обобщенной силы подсчитаем виртуальную работу при изменении обобщенной координаты

И полученное выражение разделим на вариацию обобщенной координаты

Обобщенная сила имеет размерность момента силы, так как обобщенной координатой является угол.
После проделанных вычислений и внесения их в (262) уравнение Лагранжа принимает вид:

Это дифференциальное уравнение малых качаний физического маятника, выведенное другим способом, было проинтегрировано в § 45.

Ответ. Гармонические колебания с периодом

Задача №5

Определить период малых колебаний маятника, состоящего из шарика, принимаемого за точку M массой m₁, укрепленного на конце невесомого стержня AM длины l. Точка А стержня находится в центре однородного диска массы m₂ и радиуса r. Диск может катиться без скольжения по горизонтальному рельсу. Стержень и диск жестко скреплены между собой (рис. 239). Движение маятника происходит в вертикальной плоскости.

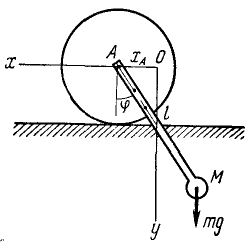
Рис. 239

Решение. Построим правую систему декартовых координат с началом в центре диска при положении устойчивого равновесия системы. Ось Oy направим вертикально вниз.

Определим связи, наложенные на систему. Диск может катиться по горизонтальному рельсу. Эта связь может быть выражена уравнением у_А = 0.Но качение диска происходит без скольжения. Такую связь можно выразить условием, чтобы скорость υ_x точки касания диска равнялась нулю. Хотя связь наложена на скорость, но для диска, катящегося в своей плоскости, она является голономной (в отличие от катящегося по плоскости шара, рассмотренного выше). В самом деле, приняв центр диска за полюс и разложив плоское движение диска на переносное поступательное вместе с полюсом и относительное вращательное вокруг полюса, получим для точки касания:

υ_А — ωr = 0 или

Интегрируя, получаем второе уравнение связи
x_A = rφ.
Следовательно, связь интегрируемая, т. е. голономная.

Система имеет одну степень свободы, ее положение определяется одной обобщенной координатой, а ее движение — одним уравнением Лагранжа. За обобщенную координату можно взять, например, абсциссу x_A центра диска или угол φ отклонения маятника от вертикали, но не надо брать за обобщенные координаты обе эти величины и составлять два уравнения Лагранжа по каждой из координат, потому что обобщенные координаты должны быть независимыми друг от друга величинами, а величины x_A и φ являются зависимыми и связаны соотношением x_A = rφ. Число уравнений Лагранжа равно числу степеней свободы. Выбор той или иной обобщенной координаты зависит от нас. Мы выберем φ. Выразим в этой обобщенной координате и обобщенной скорости φ кинетическую и потенциальную энергии системы. Определим сначала координаты шарика М, принимаемого за материальную точку, учитывая, что по уравнению связи x_A = rφ:

x= rφ—l sin φ; y = l cosφ.

Продифференцировав по времени, найдем проекции скорости:

Определим квадрат полной скорости точки М:

υ 2 _M = (r 2 + l 2 -2rl cos φ) φ 2

и кинетическую энергию точки М:

Кинетическую энергию диска определим по формуле Кёнига, учитывая, что x_A = rφ:

Кинетическая энергия системы равна сумме кинетических энергий точки M и диска:

Потенциальная энергия определяется с точностью до произвольной постоянной (см. § 49) и этим обстоятельством следует воспользоваться так, чтобы в положении равновесия, при котором все обобщенные координаты равны нулю, потенциальная энергия также равнялась нулю. По теореме Дирихле, равновесие устойчиво, если около этого положения имеется область, в которой потенциальная энергия является определенно-положительной функцией обобщенных координат. Это имеет место в нашем случае:

П= m₁gl (l — cos φ) (при φ = 0 П = 0; при φ ≠ О П > 0)

Функция Лагранжа L=T — П:

Подсчитаем величины, входящие в уравнение (264):

Колебания малые, и мы полагаем sin φ ≈ φ, cos φ ≈ 1 и пренебрегаем малыми величинами второго и высшего порядка, а также произведениями малых величин. Уравнение движения системы принимает вид:

Интегрируя, получим уравнение гармонических колебаний (см. §39). Конечно, частота этих колебаний не может зависеть только от масс, но зависит и от их распределения. Система представляет собой своеобразный физический маятник, и квадрат частоты свободных колебаний пропорционален статическому моменту веса и обратно пропорционален моменту инерции маятника относительно мгновенной оси.

Ответ.

Задача №6

Определить частоту свободный поперечных колебаний двухопорной балки, изображенной на рис. 240. На балке находится груз весом mg; расстояния от груза до опор балки равны а и b. Сечеиие и материал балки считать известными, весом балки пренебречь.

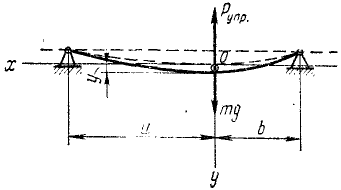
Рис. 240

Решение. Система имеет одну степень свободы. Построим декартовы координаты с началом в центре масс груза при равновесном положении системы и направим ось Oy вертикально вниз. За обобщенную координату системы примем ординату ус центра масс.

Выразим в обобщенной координате и обобщенной скорости кинетическую и потенциальную энергии системы. Массой балки пренебрегаем, и кинетическая энергия системы равна кинетической энергии груза при его поступательном движении:

Несколько сложнее определить потенциальную энергию, потому что система находится в потенциальном поле силы тяжести и в потенциальном поле упругости балки и полная потенциальная энергия П = П₁ + П₂. Потенциальная энергия системы в поле силы тяжести

Потенциальную энергию сил упругости найдем из разности двух частных ее значений: при прогибе (j+y) и при нулевом положении, при котором прогиб балки в месте расположения груза равен f:

Заметим, что при равновесном положении системы потенциальная энергия, согласно теореме Дирихле, должна иметь минимум, а потому ее производная

должна обратиться в нуль, если вместо у подставить нуль — его значение, соответствующее равновесному положению системы,

Следовательно, потенциальная энергия системы

Здесь с—коэффициент жесткости балки и, поскольку сечение и материал балки известны, может быть определен по формулам сопротивления материалов:

где E—модуль упругости материала, J_э—экваториальный момент поперечного сечения балки.
Определим теперь члены уравнения (263):

После подстановки имеем

Это уравнение выражает малые колебания системы. Разделив «коэффициент жесткости» с на «коэффициент инерции» т, найдем квадрат частоты колебании системы, и для получения ответа остается только извлечь квадратный корень.

Ответ.

Малые колебания бифилярного подвеса

Задача №7

К концам М₁ и М₂ тонкого однородного стержня (рис. 241, а) массы m и длины 2α подвязаны две невесомые нити одинаковой длины l. Верхние концы N₁ и N₂ нитей неподвижно закреплены на горизонтальной прямой на расстоянии 2α друг от друга. Стержень повернули на малый угол вокруг центральной вертикальной оси и отпустили без начальной скорости. Исследовать малые колебания.

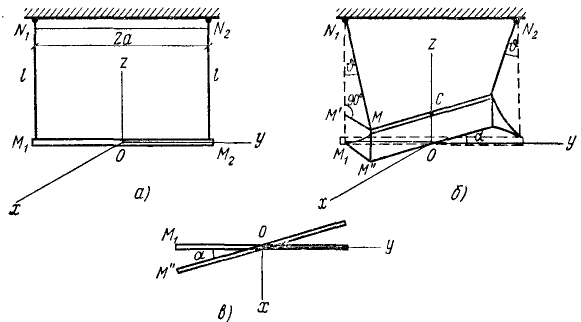
Рис. 241

Решение. При заданном движении будет изменяться высота центра масс стержня, но он не может отклоняться в сторону. Положение системы определяется высотой центра масс, углом поворота стержня вокруг вертикальной оси и углом отклонения нитей от вертикали. Но эти параметры зависят друг от друга, система имеет одну степень свободы, положение ее определяется одной обобщенной координатой, а движение —одним уравнением Лагранжа. Это уравнение удобно записать в форме (263), так как система находится в потенциальном поле тяжести и единственной активной силой системы является вес стержня.

За обобщенную координату нельзя выбрать высоту центра масс, потому что обобщенная координата должна однозначно определять положение системы, а каждому положению центра масс соответствуют два положения системы. Угол поворота стержня вокруг вертикальной оси можно принять за обобщенную координату, но удобнее в качестве таковой выбрать угол наклона нитей к вертикали, так как через этот угол легко выразить потенциальную энергию системы. Построим прямоугольную систем) координат, как показано на рисунке. Пусть в произвольное мгновение t угол поворота стержня был α, а угол наклона нитей О (рис. 241, б). Спроецируем стержень на плоскость хОу (рис. 241, в). Равнобедренный треугольник M»OM₁ и прямоугольный треугольник N₁M’M имеют равные стороны М’М = M₁M»:

Эти два равенства позволяют выразить угол α в обобщенной координате :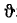

Определим в обобщенной координате и положение центра масс:

z_C = l — l cos

Переходим теперь к вычислению входящих в (263) кинетической и потенциальной энергии системы.
Кинетическую энергию определим по формуле Кёнига, но чтобы выразить ее в обобщенных координате и скорости, продифференцируем по времени выражения, полученные для z_с и α:

Подставляя эти величины в (217) и учитывая, что стержень длиной 2a имеет момент инерции 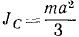получим довольно сложное выражение:

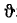
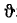
При малых колебаниях можно положить cos 2 =l и sin 2 = 0:

Вычисляя потенциальную энергию П системы, так определим постоянную С, чтобы П обращалось в нуль при 0 = 0:

П = mgl (1 — cos ).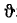

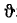
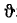
Как видно из этого равенства, при = 0 потенциальная энергия системы имеет минимум, что, по теореме Дирихле (см. § 49), означает устойчивое равновесие. Разложим cos в ряд. Тогда

Отбросив все члены выше второго порядка, получим приближенно

Теперь вычислим члены уравнения Лагранжа:

Подставляя в (263), получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Решение его нам хорошо известно. Оно выражает малые колебания системы, период которых:

Заметим, что если к стержню присоединить тело с неизвестным моментом инерции и из опыта определить период τ₁ колебания бифилярного подвеса вместе с телом, то можно определить момент инерции тела.

Ответ. Малые колебания с периодом

Колебания системы с двумя степенями свободы

Малые колебания системы с двумя степенями свободы являются линейным наложением двух главных колебаний

Малые колебания системы с двумя степенями свободы около положения устойчивого равновесия, описываемые изменением обобщенных координат, представляют собой линейные наложения двух так называемых главных, пли собственных, колебаний системы. В каждом из главных колебаний между амплитудами имеется постоянное соотношение, зависящее от параметров системы, но не зависящее от начальных данных. Каждому из главных колебаний соответствует своя собственная частота, в общем случае отличная от частоты другого собственного колебания системы, и фаза. Колебание системы с двумя или с большим числом степеней свободы, представляющее линейное наложение гармонических колебаний, обычно является сложным и может оказаться даже не периодическим. Поэтому выражения частота или период колебаний для системы, у которой число степеней свободы больше единицы, имеет смысл только по отношению к отдельным главным колебаниям системы. В системе с двумя степенями свободы нетрудно так подобрать начальные данные, чтобы какое-либо одно из двух главных колебаний отсутствовало, тогда можно наблюдать оставшееся главное колебание системы.

Решим задачу на малые колебания системы с двумя степенями свободы.

Двойной математический маятник

Задача №8

Две материальные точки M₁ массы m₁ и M₂ массы m₂ (рис. 242) связаны невесомой нерастяжимой нитью длины l₂, а точка M₁ связана, кроме того, такой же идеальной нитью длины l₁ с неподвижной точкой О. Определить собственные частоты малых колебаний системы в вертикальной плоскости xOy 2 .

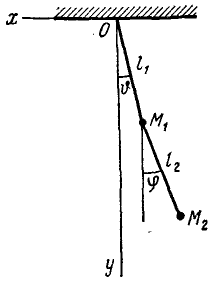
Рис. 242

Решение. По условию, маятник движется в одной вертикальной плоскости; система имеет две степени свободы и движение описывается двумя уравнениями Лагранжа. Система находится в потенциальном поле тяжести и никаких активных сил, кроме сил тяжести, на систему не действует, поэтому уравнения Лагранжа напишем в виде (263).

Выберем за обобщенные координаты углы О и φ наклона нитей к вертикали и выразим через них декартовы координаты точек

Продифференцировав по времени, возведя в квадрат и складывая, найдем квадраты скоростей точек:

Теперь легко вычислить кинетическую энергию T системы:

Определяя потенциальную энергию П, выберем так произвольную постоянную С, чтобы при равновесии системы П равнялось нулю:

Пусть произвольная постоянная C означает потенциальную энергию системы при 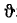= φ=180 o , т. е. положим

Теперь потенциальная энергия системы при любых значениях обобщенных координат выражается равенством

При 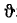= φ = 0 величина П равна нулю, при остальных значениях П > 0, т. е. П является определенно положительной функцией обобщенных координат.

Подсчитаем члены уравнений (263) Лагранжа:

Подставляя эти величины в уравнения (263), получим следующие точные уравнения движения системы:

Ограничимся малыми колебаниями системы и заменим косинусы единицей, а синусы малых углов — углами. Пренебрежем членами, содержащими квадраты или произведение скоростей, и для упрощения записи обозначим m₂:m₁ = μ. Уравнения примут вид:

Второе уравнение позволяет упростить первое:

Частные решения этой системы уравнений мы будем искать в виде

т. е. в предположении, что обе обобщенные координаты изменяются гармонически, с одинаковыми частотами и фазами, но с разными амплитудами. Подставляя значения углов и их вторых производных в дифференциальные уравнения и сокращая на sin (kt + α), найдем

Эта система двух уравнений, линейных относительно B₁ и B₂, может иметь отличные от нуля решения, если определитель системы равен нулю:

В теории колебаний это уравнение называют вековым уравнением, или уравнением частот, так как оно позволяет определить частоты главных колебаний системы. При условиях нашей задачи это решение записано в ответе. Оба периода главных колебаний различны между собой и зависят от отношения μ масс точек и от длины l₁ и l₂ нитей. Один из периодов близок к периоду качаний математического маятника длины l₂, другой — к периоду маятника длины l₁. Изменяя длину одного из маятников, мы можем период соответствующего главного колебания сделать больше или меньше периода второго главного колебания, однако мы не смогли бы добиться, чтобы оба главных периода качания двойного маятника были бы в точности одинаковы. Этот парадокс был открыт Стоксом и объясняется тем, что написанное выше уравнение частот не имеет одинаковых корней, при которых возможны устойчивые колебания двойного маятника.

Ответ.

Задача №9

В условии задачи вместо жесткого соединения невесомого стержня МЛ с диском сделано шарнирное соединение в точке Л, остальные условия не изменены (рис. 243).

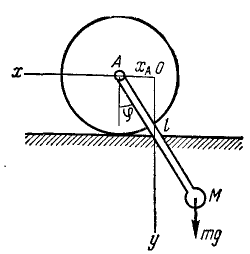
Рис. 243

Решение. В отличие от системы, рассмотренной в задаче № 195, здесь система имеет две степени свободы и движение ее может быть описано двумя уравнениями Лагранжа. За обобщенные координаты примем независимые величины φ и х_А. При подсчете кинетической энергии скорость точки А мы уже не можем определять как rφ, а должны писать х_А. Выражение потенциальной энергии остается прежним и функция Лагранжа имеет вид

Вычислим члены уравнений Лагранжа:

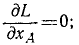
Напишем оба уравнения Лагранжа:

Мы ищем период малых колебаний системы, поэтому, допустив применяемые в подобных случаях упрощения, перепишем эти уравнения в таком виде:

Определяя 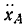из первого уравнения и подставляя во второе, получим

Множитель, стоящий перед обобщенной координатой, выражает частоту колебаний.
Ответ. Период малых колебаний маятника

Задача №10

Составить дифференциальные уравнения свободных вертикальных колебаний автомобиля, происходящих параллельно плоскости его симметрии, если масса приведенной в колебание системы pa⅞ιιa т, а момент инерции относительно поперечной оси, проходящей через центр масс, равен .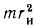

Решение. На рис. 244 вверху изображен автомобиль, а внизу его динамическая схема. Деформации кузова пренебрежимо малы по сравнению с осадкой опор, поэтому в динамической схеме мы считаем раму совершенно жесткой. Кроме того, мы полагаем, что горизонтальные колебания системы невозможны.

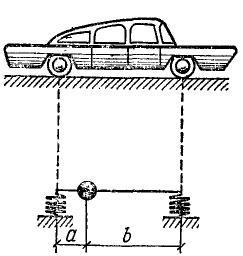
Рис. 244

Построим оси декартовых координат с началом в центре масс при равновесном положении системы, направив ось ординат по вертикали вниз. Система обладает двумя степенями свободы и за обобщенные координаты q_l и q₂ примем ординату центра масс и угол наклона рамы к горизонтальной плоскости.
Кинетическую энергию системы определим по формуле Кёнига:

Для определения потенциальной энергии заметим, что если рама автомобиля опустится на q₁ и при этом наклонится на q₂, то задняя опора сожмется на q₁+ αq₂, а передняя на q₁+ bq₂. Учитывая жесткости рессор и пиевматиков, обозначим через c₁ и c₂ приведенные жесткости задней и передней подвески автомобиля. Тогда потенциальную энергию системы определим аналогично тому, как это было сделано в примере § 49:

Подставляя найденные значения T и П в уравнения Лагранжа, получим ответ.

• Сложение двух сил
• Разложение силы на две составляющие
• Определение равнодействующей сходящихся сил
• Равновесие сходящихся сил
• Количество движения
• Момент количества движения
• Мощность и работа силы
• Потенциальная энергия

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Теоретическая механика. Малые колебания с одной степенью свободы.

В качестве примера разберем решение типового варианта домашнего задания по данной теме. Возьмем вариант 32, чтобы никому не было обидно, ну а кое-кому, возможно, сказочно повезло.

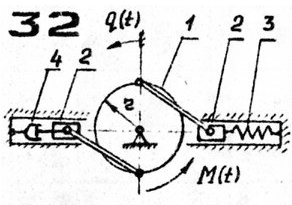
Итак, вот условие задания.

К нему прилагается таблица с цифрами, мы будем решать в общем виде. Обычно в подобных заданиях всегда заданы все массы, упругость пружины, размеры звеньев, коэффициент сопротивления демпфера и граничные условия для решения дифференциального уравнения колебаний.

Все подобные задачи решаются по одному и тому же алгоритму. Первым делом задаемся обобщенной координатой. За нас это уже сделали составители задания, обобщенная координата указана на рисунке как q(t) — это угловой поворот шестерни 1.

Следующий шаг — записать через q скорости ключевых точек механизма. К ним относятся — скорости центров тяжести всех тел, обладающих массой, угловые скорости тел, совершающих вращательное движение, скорость точки закрепления пружины, скорость поршня демпфера. В нашем случае это угловая скорость шестерни 1 и линейные скорости ползунов 2.

Уравнения, связывающие скорости с обобщенной координатой, называются уравнениями связей. Для нашей системы они выглядят несложно.

Третий шаг — нужно записать кинетическую энергию для всей системы. Для этого нужно посчитать кинетическую энергию всех тел, обладающих массой. В нашем случае шестерня 1 движется вращательно, ползуны 2 — поступательно. Кинетическая энергия считается следующим образом:

Из выражения для кинетической энергии мы определим обобщенный коэффициент инерции а. Поскольку

Теперь время записать выражения для потенциальной энергии системы. Центры тяжести тел в нашем механизме не перемещаются по вертикали, значит, силы тяжести вклад в потенциальную энергию не вносят. Была ли пружина деформирована до начала колебаний? Не была. Значит, при повороте шестерни 1 на угол q пружина растягивается на величину qr (это следует из уравнения связи для V2, перемещения связаны теми же соотношениями, что и скорости).

Из выражения для потенциальной энергии мы определим обобщенный коэффициент жесткости с. Поскольку

Теперь работаем с диссипативной функцией Релея. Она записывается следующим образом

Здесь V2 — это скорость поршня в демпфере, в нашем случае она равна скорости ползуна 2.

Из выражения для Ф мы определим обобщенный коэффициент вязкого сопротивления b. Поскольку

Осталось разобраться с возбуждающей колебания силой. В нашем случае происходит динамическое возбуждение колебаний (когда к механизму приложена внешняя сила F(t), ну или момент М(t), как у нас). Нужно записать обобщенную силу, это проще всего сделать через элементарную работу внешней силы на малом приращении координаты. Выглядит так

Отсюда можно выразить амплитуду возбуждения. Поскольку

Собственно, мы вплотную подошли к записи дифференциального уравнения колебаний. Для этого нам нужны значения обобщенных коэффициентов:

Четыре цифры. В подавляющем большинстве задач всегда не равны 0 коэффициенты a и с. Если в задаче нет демпфера, то b=0. Если нет возбуждения, то H=0.

В общем виде, дифференциальное уравнение колебаний записывается так

Его приводят к каноническому виду

Когда диффур записан, остается его только решить. Алгоритм решения мы рассматривали ранее.

Надеемся, что мы немного прояснили для вас алгоритм решения подобных задач. Подытожим.

1) Выбрать обобщенную координату

2) Записать уравнения связей

3) Записать кинетическую энергию (найти обобщенный коэффициент инерции а)

4) Записать потенциальную энергию (найти обобщенный коэффициент жесткости c)

5) Записать диссипативную функцию Релея (найти обобщенный коэффициент сопротивления b)

6) Записать обобщенную возбуждающую силу (найти амплитуду H)

7) Записать ДУ, привести его к каноническому виду, решить.

Разумеется, есть ряд фишек и тонкостей в каждом отдельно взятом механизме, но общий ход размышлений именно такой. Дерзайте, и у вас все получится. Если возникают вопросы, обращайтесь.

Колебания системы с одной степенью свободы

Колебания системы с одной степенью свободы

• Механическая система с одной степенью свободы имеет одну обобщенную координату q, и ее движение описывается одним уравнением Лагранжа ди дк дк (1). Обобщенная сила Q может рассматриваться как состоящая из трех частей: Q = Qn + Q ‘+ QB, где Qn — обобщенная сила потенциальных сил. Потенциальная энергия в общем случае зависит от координат точки системы, поэтому она зависит от обобщенной координаты q и обобщается по формуле Qn = —dP / dq Оно не зависит от скорости q.

В случае нестационарного силового поля и нестационарного силового поля потенциальная энергия явно зависит от времени. 0F включает в себя обобщенную часть силы, которая является результатом действия сопротивления. Сила сопротивления зависит как от числового значения, так и от направления скорости системной точки. Далее рассматривается случай линейного сопротивления, когда сопротивление системных точек пропорционально скорости этих точек и направлено в противоположном направлении. Часть обобщенной силы QB является производной от так называемых вынужденных или возмущающих сил, которые в основном зависят от времени.

Поступательная часть перемещения тела зависит от выбора точки, вместе с которой перемещается тело, а вращательная часть перемещения вокруг оси или вокруг точки не зависит от выбора точки. Людмила Фирмаль

Далее рассмотрим случай гармонических возмущений, где Q изменяется во времени в соответствии с законом синуса. В общем случае зависимость QB от времени может быть расширена с помощью ряда Фурье для учета дифференциальных уравнений движения для каждого синусоидального члена. Естественная линейная вибрация системы Под действием нескольких потенциальных сил, то есть b = -dlJ / dq, рассмотрим небольшую вибрацию системы с одной степенью свободы. Сопротивление и возмущение Там нет власти. Такая вибрация называется внутренней или свободной.

Когда система движется, обобщенные координаты, скорость и ускорение достаточно малы, чтобы игнорировать все члены q, q и q, которые являются квадратичными или более высокими в терминах уравнения Лагранжа (1), то есть, члены, которые включают эти квадраты Если система имеет малую вибрацию, то для обобщенной координаты q получается линейное дифференциальное уравнение. Колебания, в которых дифференциальное уравнение является линейным, называются линейными. Небольшие колебания линейны. Однако линейность не обязательно является небольшой вибрацией.

В общем, ограничения, которые должны быть наложены на величину, характеризующую движение, чтобы вибрация была уменьшена, могут быть установлены только после того, как проблема будет полностью решена в предположении, что вибрация мала. Далее рассматриваются только небольшие колебания или, если не маленькие, линейные колебания. Дифференциальное уравнение для естественной линейной вибрации системы. Чтобы вывести линейное уравнение малых собственных колебаний из уравнения Лагранжа (1), кинетическая и потенциальная энергии должны быть последовательно растянуты вблизи положения равновесия системы с q = 0.

Рассмотрим систему, в которой голономная, идеальная, неосвобожденная и фиксированная связь состоит из N точек и движется около положения равновесия. Ее кинетическая энергия При сделанных предположениях о совместной стационарности радиус-вектор r * каждой точки в системе зависит от времени только через обобщенную координату q. Следовательно, rk = — ^ q. Подстановка этого gk в уравнение кинетической энергии дает r = 72l ^ 2. Как и в случае с gk, величина A может зависеть только от q, а не от q. Когда A (q) расширяется вблизи q = 0 степенного ряда, Далее индекс 0 означает, что соответствующее значение вычисляется с q = 0.

Чтобы получить кинетическую энергию в терминах квадратичного и более низкого членов для q и q, достаточно получить только постоянное значение Ao из разложения A (. Где q0 и q0 — начальные значения обобщенных координат и обобщенной скорости. Используйте выражения q и q с r = 0, чтобы получить Ci = Людмила Фирмаль

Обратите внимание на основные характеристики естественной линейной вибрации. Рисунок 111 Амплитуда этих собственных линейных колебаний системы является гармонической величиной постоянной вибрации И определяется начальными условиями. Период колебаний также является постоянным значением и не зависит от амплитуды и, следовательно, начальных условий. Величина периода является характеристикой системы вибрации, т.е. Он определяется только коэффициентом инерции а и жесткостью с. Независимость периода вибрации от амплитуды называется виброизохронизмом. Уникальная линейная вибрация.

При отсутствии возмущающих сил они могут возникать только при начальных условиях, которые не равны нулю. То есть в первый момент система имеет ненулевую начальную обобщенную координату q0 или начальную обобщенную скорость q0. Гармоническое колебание точки при наличии линейной восстанавливающей силы вызвано начальным отклонением точки x0, начальной скоростью a0 или обоими. Гармоническая вибрация имеет характеристику, заключающуюся в том, что, как только она возникает в определенной точке, она продолжается до тех пор, пока не произойдет изменение параметров вибрации, если не будет другого влияния.

Однако обычно вибрация всегда сопровождает сопротивление, и природа естественной вибрации меняется. В дополнение к графику колебаний его колебательное движение может быть представлено на фазовой плоскости — плоскости переменных q и q, называемых фазовыми переменными. Для точечных колебаний фазовыми переменными являются x и v = x. Давайте создадим фазовый портрет гармонической вибрации точки. У нас есть x — грех (£ f + a); v = x = Akcos (kt + v). Рисунок 112 Удалите время t из этих уравнений, чтобы получить эллиптическое семейство в фазовой плоскости (x, p). Эти кривые (рис. 112), в зависимости от параметра A, называются фазовыми траекториями.

Семейство фазовых траекторий зависит от следующих амплитуд: Вариация определяется начальными условиями. Каждая фазовая траектория соответствует паре начальных значений x0 и v0. Точка равновесия на фазовой плоскости соответствует началу координат x = 0, a = 0. Когда точка массы гармонично колеблется, ее координата x и скорость v изменяются со временем. В результате каждый момент на фазовой плоскости соответствует определенной позиции точки изображения с координатами x и V. В течение одного полного гармонического колебания (периода) точка изображения представляет эллипс на фазовой плоскости. Отметим, что замкнутые фазовые траектории соответствуют периодическим колебаниям на фазовой плоскости и наоборот.

Тип фазовой траектории характеризует устойчивость или неустойчивость положения равновесия и малость вибрации. Консервативные системные фазовые траектории могут быть построены с использованием интеграции энергии. Каждая фазовая траектория соответствует определенному значению полной механической энергии. Если дифференциальное уравнение для колебательного движения является нелинейным, изучение движения с использованием фазовых траекторий является одним из наиболее часто используемых методов. mx = —cx \ x + fc2x = 0; k = ^ / s! т. Если вы не выберете место статического равновесия в контрольной точке, уравнение будет иметь постоянную правую часть. Другими словами, это становится неравномерным.

Решение дифференциального уравнения может быть выражено в следующем виде: x = C1cos * / + C2sin * (; ”= x = −C, * -sinfc (+ C2 * cosb. Константы C и C2 определяются начальными условиями. Время 1 = 0, начальная скорость x = b0 = 10 см / с; х = х0 = х0-х „= 8-5 = 3 см; k = y / eim = y / glkcl = y / 99OI5 = 14 с «’ Константа С ‘! И с2. Если выражение для x и x равно 1 = 0, значение равно C | = xo = 3cm. C2 = »o / * = 0,71 см Уравнение движения груза принимает вид x = 3cos 141 + 0,71 sin 141 см Используйте формат амплитуды. амплитудное 4 = х / с? + C? =, / 9 + 0,50 х 3,08 см.

Начальная фаза а. sin a = C, l = 0,97> 0; cos a = C2 / A = 0,71 / A> 0. Следовательно, угол a находится в первой четверти и, в зависимости от значения (например, sina), a = 1,34 = 0,43 л. Уравнение движения для нагрузки в амплитудной форме имеет вид ,

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института