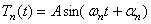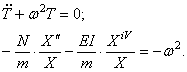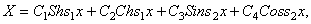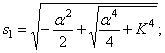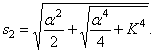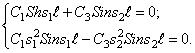Метод Фурье
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Метод Фурье, или метод разделения переменных, является одним из наиболее распространенных методов решения уравнений с частными производными. Рассмотрим этот метод, обратившись к простейшей задаче о свободных колебаниях однородной струны длины i, закрепленной на концах. §4. Свободные колебания однородной струны, закрепленной на концах Задача о свободных колебаниях однородной струны с закрепленными концами сводится к решению уравнения при граничных условиях и начальных условиях.
Метод Фурье Задачу (1 )-(3) называют смешанной: она содержит и начальные и граничные условия. Решение задачи начнем с поиска частных решений уравнения (1) вида При этом будем предполагать, что каждое из них удовлетворяет граничным условиям (2), но не равно нулю тождественно. Подставляя функцию и<х, t) в форме (4) в уравнение (1), получаем ИЛИ Последнее равенство (его левая часть зависит только от а правая — только от х) возможнолишь втом случае, если обе его части не зависят ни от ty ни от х,т.е. равны одной и той же постоянной.
Обозначим эту постоянную (разделения) через (-А), Из равенства (5) получаем два обыкновенных дифференциальных уравнения Граничные условия (2) дают откуда (T(t) £ 0) следует, что функция Х(х) должна удовлетворять граничным условиям Чтобы получить нетривиальные решения tt(x, t) вида (4), удовлетворяющие граничным условиям (2), необходимо найти нетривиальные решения уравнения удовлетворяющие граничным условиям.
Таким образом, мы приходим к следующей задаче: найти значения параметра А, при которых существуют нетривиальные решения задачи (7)-(8), а также сами эти решения. Такие значения параметра А называются собственными значениями, а соответствующие им нетривиальные решения — собственными функциями задачи (7)-(8). Сформулированную таким образом задачу называют задачей Штурма—Лиувилля. Найдем собственные значения и собственные функции задачи (7)-(8).
Рассмотрим отдельно три случая, когда 1.
При общее решение уравнения (7) имеет вид Потребовав выполнения граничных условий (8), получим (6) (7) Так как определитель системы (9) отличен от нуля, то . Следовательно, Х(х) = 0, т. е. при нетривиальных решений задачи не существует. (9) 2. При А = 0 общее решение уравнения (7) имеет вид Граничные условия (8) дают откуда С, = С2 = 0, и следовательно, при А = 0 нетривиальных решений задачи (7)-(8) также не существует. 3.
При Л > 0 общее решение уравнения (7) имеет вид Потребовав выполнение граничных условий (8), получим Система (10) имеет нетривиальные решениятогда и толькотогда, когда определитель системы равен нулю, Метод Фурье будут собственными функциями задачи. Собственные функции определены с точностью до постоянного множителя, который мы выбрали равным единице. При А = А* общее решение у равнения (6) имеетвид ктга кчга где Аки Bk — произвольные постоянные. Таким образом, функции удовлетворяют уравнению (1) и граничным условиям (2) при любых Ак и Вку В силу линейности и однородности уравнения (1) всякая коневая сумма решений будет также решением уравнения (1).
То же справедливо и для ряда если он сходится равномерно и его можно дважды почленно дифференцировать по х и по t. Поскольку каждое слагаемое в ряде (11) удовлетворяет граничным условиям (2), то этим условиям будет удовлетворять и сумма u(s, t) этого ряда. Остается определить в формуле (11) постоянные .4* и Вк так, чтобы выполнялись и начальные условия (3). Продифференцируем формально ряд (11) по t.
Имеем Полагая в соотношениях (l 1) и (12) t = 0, в силу начальных условий (3) получим Формулы (13) представляют собой разложения заданных функций вряд Фурье по синусам в интервале Коэффициенты разложений (13) вычисляются по известным формулам / I Теорема 2. Если и удоъчетворяет условиям и удовлетворяет условию то сумма tx(x, £) ряда (11), где -А* и В* опредыяются формулами (14), имеет в области непрерывные частные производные до второго порядка включительно по каждому из аргументов, удовлетворяет уравнению (1), граничным условиям (2) и начальным условиям (3), т. е. является решением задачи (1 )-(3).
Пример. Найти закон свободных колебаний однородной струны длины I, закрепленной на концах, если в начальный момент t = 0 струна имеет форму параболы — const), а начальная скорость отсутствует. 4 Задача сводится к решению уравнения при граничных условиях и начальных условиях.
Возможно вам будут полезны данные страницы:
Метод Фурье
Применяя метод Фурье, ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде Подставляя «(*,*) в форме (4) в уравнение (1) и разделяя переменные, получим откуда причем в силу (2) Как было установлю но выше, собственные значения задачи (7)-(8) а соответствующие собственные функции Для А = Ащ общее решение уравнения (6) имеет вид пяа ижа Будем иска тъ решение исходной задачи в виде ряда Для определен ия коэффициентов -4Я и Z?„ воспользуемся начальными условия ми (3).
| Имеем Из формулы (II) срезу |
получаем, что 2?„ = 0 для любог о п, а из (10) Метод Фурье откуда, интегрируя по частям дважды . находи м . Подставляя наеденные значения А, и в ряд (9), получим решение поставленной задачи , Замечание. Если начальные фукхдда не удовлетворяют условиям теоремы 2, то дважды непрерывно дифференцируемого решения смешанной задачи (1)-(3) может и не существовать.
Однако если , то ряд (II) сходетс* равномерно при и любом t и определяет непрерывную функюао u(xtt). В этом случае можно говорить лишь об обобщенная решении задачи. Каждая из функций определяет так называемые собств енные колебания струны, закрепленной на концах. При собственных колебаниях, отвечающих к = 1, струна издает основной, самый низкий тон.
При колебаниях, соответствующих ббльшим Л.она издает более высокие тоны, обертоны. Записав *) в виде заключаем, что собственные колебания струны — стоячие волны, при которых точки струны совершают гармонические колебания с амплитудой Нк sin частотой Метод Фурье Мы рассмотрели случай свободных колебаний однородной струны, закрепленной на концах. Рассмотрим теперьслуч ай других граничных условий.
Пусть, например, левый конец струны закреплен, u(0, t) = 0, а правый конец х — 1 упругосвязан со своим положением равновесия, что соответствует условию . Нетривиальное решение u(x, t) уравнения (1), удовлетворяющее поставленным граничным условиям, будем опять искать в виде В результате подстановки в уравнение (1) приходим к следующей задаче о собственных значениям: найти такие значения параметра Л, для которых дифференциальное уравнение при граничных условиях имеет нетривиальные решения Х(х). Общее решение уравнения (15) имеет вид (А > 0)
Первое из граничных условий
Первое из граничных условий (16) дает С\ = 0, так что функциями Х(х) с точностью до постоянного множителя являются sin у/Хх. Из второго граничного условия Положим А = ir. Тогда Для отыскания и получаем трансцендентное уравнение. Корни этого уравнения можно найти графически, взяв в плоскости (f, z) сечения последовательных ветвей кривой z = tg(i//) прямой линией z = (рис. 7).
Обе части уравнения (18) — нечетные функции относительно р, поэтому каждому положительному корню i/fc соответствует равный ему по абсолютной величине отрицательный корень. Поскольку изменение знака Uk не влечет за собой появления новых собственных функций (они только изменят знак, что несущественно), достаточно ограничиться положительными корнями уравнения (18).
В результате опять получается последовательность собственных значений и отвечающие им последовательности собственных функций и собственных колебаний Кстати, для n-ой собственной частоты ип получается асимптотическое соотношение в частности, для I = т имеем Если правый конец струны х = I свободен, получаем cos vl = 0. Отсюда ul = § + тиг, так что в случае свободного конца собственные значения и собственные функции соответственно равны
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Лекция 2. Вывод уравнения колебания струны
Рассмотрим струну длины l
Струной будем называть тонкую туго натянутую упругую нить.
При построени математической модели колебаний струны будем рассматривать малые колебания, происходящие в одной и той же плоскости. Пусть в состояниии покоя струна расположена вдоль оси Ox на отрезке [0,l] и при колебании каждая точка перемещается перпендикулярно оси (поперечные колебания). Тогда отклонение любой точки струны в произвольный момент времени U есть функция U(x,t) (см. рис.2).
Предположим, что натяжение столь велико, что силой тяжести и сопротивлением при изгибе можно пренебречь. Кроме того, в силу малости колебаний, будем пренебрегать также величинами высшего порядка малости по сравнению с производной Ux.
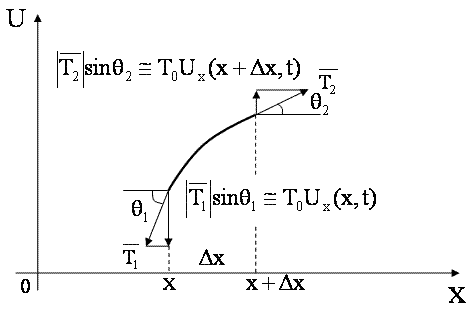
Рис. 3
Выделим малый участок струны (см. рис.3) и рассмотрим силы, действующие на него. Так как струна не сопротивляется изгибу, то ее натяжение 
направлено по касательной к струне в точке x. Более того, в рамках наших предположений можно считать величину силы натяжения постоянной. В самом деле, длина любого участка струны (величиной Ux 2 можно пренебречь). С ледовательно, в соответствии с законом Гука 
.
Пусть ρ ( x )- линейная плотность в точке x , а γ ( x , t )- плотность внешних сил, действующих на струну в момент времени t, и направленных перпендикулярно Ox .
Результирующая сила, действующая на участок струны [ x , x +∆ x ] в направлении перпендикулярном оси OX , равна (см. рис. 3)
.
При выводе этой формулы учитываем, что при малых колебаниях
По второму закону Ньютона произведение массы на ускорение равно действующей силе mw = F , где w=Utt, поэтому
ρ ∆ xUtt = T 0[ Ux ( x + ∆ x , t )- Ux ( x , t )]+ γ ( x , t ) ∆ x .
Разделим обе части равенства на Δx и устремим Δx к нулю:
ρ ( x ) Utt = T 0[ Ux ( x + ∆ x , t )- Ux ( x , t )]/ ∆ x + γ ( x , t ) .
Это уравнение называется уравнением вынужденных колебаний струны. Если струна однородная, то есть ρ ( x )= const , то уравнение (3) обычно записывают в виде
Utt = a 2 Uxx + f ( x , t ),где a 2 = T 0/ ρ ; f ( x , t )= γ ( x , t ) / ρ .
В том случае, когда на струну не действуют внешние силы, получается уравнение свободных колебаний струны
Уравнения (3) и (4) являются одномерными волновыми уравнениями (соответственно, неоднородным и однородным).
Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.
Начальные условия и граничные условия.
Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за t=0. В результате возникает задача Коши. Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для нестационарных уравнений, то есть таких уравнений, которые описывают нестационарные (зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости, или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов, мы тем самым не будем учитывать влияния отраженных волн.
Для волнового уравнения Utt = a 2 Uxx задаются два начальных условия U | t =0 = φ ( x ), Ut | t =0 = ψ ( x ). Иногда их записывают иначе: U ( x , 0) = φ (х), Ut ( x , 0) = ψ (х). Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие — начальные скорости точек струны. В случае волнового уравнения Utt = a 2 Δ U на плоскости или в пространстве задаются те же два начальных условия, только функции φ и ψ , соответственно, будут зависеть от двух или трех переменных.
Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются граничными условиями или краевыми условиями.Для уравнения колебаний струны часто задаются условия U | x =0 = 0, U | x = l = 0. Иначе их записывают еще и гак: U (0, t )=0, U ( l , t ) = 0. Эти условия физически означают, что концы струны закреплены (то есть отклонения при х = 0 и при х = l в любой момент времени равны нулю). Можно задавать и другие условия на концах струны, например, Ux |х=0= 0 , Ux |х= l = 0. Такие условия возникают в следующей задаче.
Пусть концы сруны перемещаются вдоль вертикальных направляющих без трения (см. рис.4).
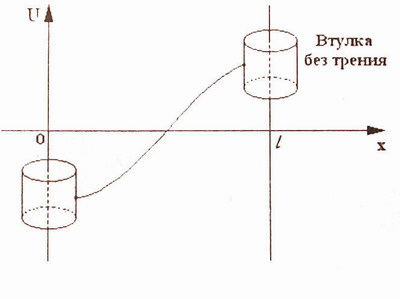
рис.4
Так как вертикальные силы, действующие на левый и правый концы струны, определяютя выражениями T 0 Ux ( O , t ) и T 0 Ux (l, t ) (см рис. 2), то записанные выше условия означают, что на концы струны не действуют никакие силы(поэтому такие условия называют еще условиями свободных концов).
Как было уже сказано, волновое уравнение Utt = a 2 Uxx описывает не только колебания струны, но и другие волновые процессы, к примеру, продольные колебания пружины, продольные колебания стержня, крутильные колебания вала. В этих задачах возникают граничные условия и других видов. Подробно такие задачи мы изучать не будем. Однако приведем основные типы граничных условий. Обычно рассматривают три типа:
Граничные условия (5), (6) и (7) называются однородными, если правые части g1(t) и g2(t) тождественно равны нулю при всех значениях t. Если хотя бы одна из функций в правых частях не равна нулю, то граничные условия называются неоднородными.
Аналогично формулируются граничные условия и в случае трех или четырех переменных при условии, что одна из этих переменных — время. Г раницей в этих случаях будет или замкнутая кривая Г, ограничивающая некоторую плоскую область, или замкнутая поверхность Ω, ограничивающая область в пространстве. Соответственно изменится и производная от функции, фигурирующая в граничных условиях второго и третьего рода. Это будет производная по нормали n к кривой Г на плоскости или к поверхности Ω в пространстве, причем, как правило, рассматривают нормаль, внешнюю по отношению к области(см.рис. 5 ) .
К примеру, граничное условие (однородное) первого рода на плоскости записывается в виде U|Γ=О, в пространстве U|Ω=0. Граничное условие второго рода на плоскости имеет вид ,а в пространстве . Конечно, физический смысл этих условий разный для различных задач.
При постановке начальных и граничных условий возникает задача об отыскании решения дифференциального уравнения, удолетворяющего заданным начальным и граничным (краевым) условиям. Для волнового уравнения (3) или (4), начальных условий U(x,0)= φ(x), Ut (x,0)=ψ(x) и в случае граничных условий первого рода (5), задача называется первой начально-краевой задачей для волнового уравнения. Если вместо граничных условий первого рода задавать условия второго рода (6) или третьего рода (7), то задача будет называться, соответственно, второй и третьей начально-краевой задачей. Если граничные условия на разных участках границы имеют различные типы, то такие начально-краевые задачи называют смешанными.
Раздел 6. Свободные колебания систем с распределёнными параметрами
Основная особенность процесса свободных колебаний систем с бесконечным числом степеней свободы выражается в бесконечности числа собственных частот и форм колебаний. С этим связаны и особенности математического характера: вместо обыкновенных дифференциальных уравнений, описывающих колебания систем с конечным числом степеней свободы, здесь приходится иметь дело с дифференциальными уравнениями в частных производных. Кроме начальных условий, определяющих начальные смещения и скорости, необходимо учитывать и граничные условия, характеризующие закрепление системы.
6.1. Продольные колебания стержней
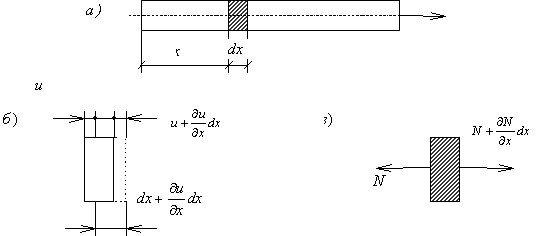
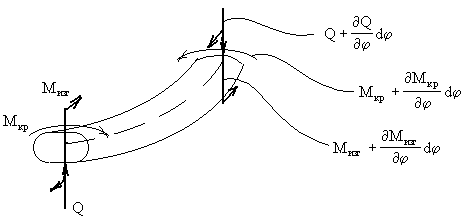
При анализе продольных колебаний прямолинейного стержня (рис.67,а) будем считать, что поперечные сечения остаются плоскими и что частицы стержня не совершают поперечных движений, а перемещаются только в продольном направлении.
Пусть u — продольное перемещение текущего сечения стержня при колебаниях; это перемещение зависит от расположения сечения (координаты x ) и от времени t . Таким образом,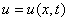 
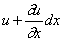
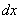
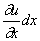
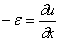
есть функция двух переменных; её определение и представляет основную задачу. Перемещение бесконечно близкого сечения равно 
, следовательно, абсолютное удлинение бесконечно малого элемента 
равно 
(рис.67,б), а относительное его удлинение 
.
Соответственно продольная сила в сечении с координатой х может быть записана в виде
, (173)
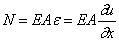
где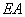 
жёсткость стержня при растяжении (сжатии). Сила N также является функцией двух аргументов – координаты х и времени t .
Рассмотрим элемент стержня, расположенный между двумя бесконечно близкими сечениями (рис.67,в). К левой грани элемента приложена сила N, а к правой – сила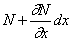 
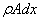
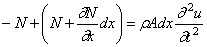
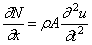
. Если обозначить через 
плотность материала стержня, то масса рассматриваемого элемента составляет 
. Поэтому уравнение движения в проекции на ось х
,
. (174)
Учитывая (173) и принимая A = const , получим
, (175)
. (176)
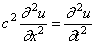
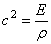
Следуя методу Фурье, ищем частное решение дифференциального уравнения (175) в виде
, (177)
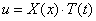
т.е. предположим, что перемещение u можно представить в виде произведения двух функций, одна из которых зависит только от аргумента х , а другая только от аргумента t . Тогда вместо определения функции двух переменных u ( x , t ) необходимо определять две функции X( x ) и T( t ), каждая из которых зависит только от одной переменной.
Подставив (177) в (174), получим
,
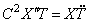
где штрихами обозначена операция дифференцирования по x , а точками – по t . Перепишем это уравнение таким образом:
.
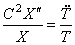
Здесь левая часть зависит только от x,а правая – только от t . Для тождественного выполнения этого равенства (при любых x и t ) необходимо, чтобы каждая из его частей была равна постоянной, которую обозначим через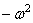 
:
; 
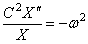
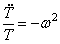
. (178)
Отсюда следуют два уравнения:
; 
. (179)
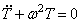
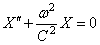
Первое уравнение имеет решение:
, (180)
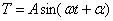
указывающее на колебательный характер, причём из (180) видно, что неизвестная величина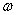 
имеет смысл частоты свободных колебаний.
Второе из уравнений (179) имеет решение:
, (181)
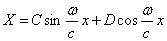
определяющее форму колебаний.
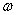
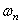
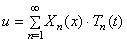
Частотное уравнение, определяющее величину , составляется путём использования граничных условий. Это уравнение всегда трансцендентное и имеет бесконечное число корней. Таким образом, число собственных частот бесконечно, причём каждому значению частоты 
соответствует своя функция Tn ( t ), определяемая зависимостью (180), и своя функция Xn ( x ), определяемая зависимостью (181). Решение (177) является лишь частным и не даёт полного описания движения. Полное решение получается путём наложения всех частных решений:
.
Функции Xn ( x ) называются собственными функциями задачи и описывают собственные формы колебаний. Они не зависят от начальных условий и удовлетворяют условию ортогональности, которое при А=const имеет вид
, если 
.
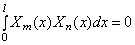
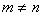
Рассмотрим некоторые варианты граничных условий.
Закреплённый конец стержня (рис.68,а). В концевом сечении перемещение u должно быть равно нулю; отсюда следует, что в этом сечении
Свободный конец стержня (рис.68,б). В концевом сечении продольная сила
(183)
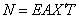
должна тождественно равняться нулю, что возможно, если в концевом сечении X’=0.
Упругозакреплённый конец стержня (рис.68,в).
При перемещении u концевого стержня возникает упругая реакция опоры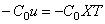 
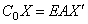
, где Со — жёсткость опоры. Учитывая (183) для продольной силы, получим граничное условие
,
если опора расположена на левом конце стержня (рис.68,в), и
,
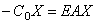
если опора расположена на правом конце стержня (рис.68,г).
Сосредоточенная масса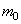 
на конце стержня.
Развиваемая массой сила инерции:
.
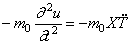
Так как, согласно первому из уравнений (179),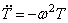 
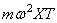
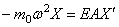
, то сила инерции может быть записана в виде 
. Получаем граничное условие
,
если масса находится на левом конце (рис.68,д), и
, (184)
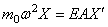
если масса связана с правым концом (рис.68,е).
Определим собственные частоты консольного стержня (рис.68,a’).
Согласно (182) и (183), граничные условия
X’=0 при х=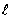 
.
Подставляя поочерёдно эти условия в решение (181), получим
D=0;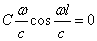 
.
Условие С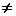 
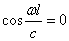
0 приводит к частотному уравнению:
.
Корни этого уравнения
(n=1,2,…)
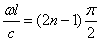
определяют собственные частоты:
(n=1,2,…). (185)
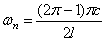
Первая (низшая) частота при n=1:
.
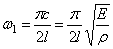
Вторая частота (при n=2):
и т. д.
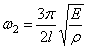
Определим собственные частоты стержня с массой 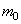на конце (рис.68,е).
Согласно (182) и (184), имеем
при х= 
.
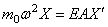
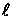
Подставляя эти условия в решение (181), получим:
D=0;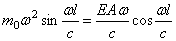 
.
Следовательно, частотное уравнение при учёте (176) имеет вид
.
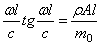
Здесь правая часть представляет собой отношение массы стержня к массе концевого груза.
Для решения полученного трансцендентного уравнения необходимо воспользоваться каким-либо приближённым способом.
При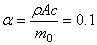 
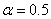
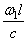
и 
значения наиболее важного низшего корня 
будут соответственно 0.32 и 0.65 .
При малом отношении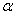 
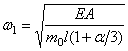
решающее влияние оказывает груз и хорошие результаты даёт приближённое решение
.
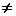
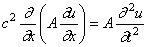
Для стержней переменного сечения, т.е. при А const , из (173) и (174) получается уравнение движения в виде
.
Это дифференциальное уравнение не поддаётся решению в замкнутом виде. Поэтому в подобных случаях приходится прибегать к приближённым методам определения собственных частот.
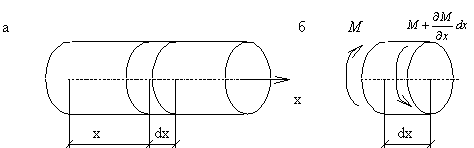
6.2. Крутильные колебания валов
Крутильные колебания вала с непрерывно распределенной массой (рис.69,а) описываются уравнениями, которые по структуре полностью совпадают с приведенными выше уравнениями продольных колебаний стержней.
Крутящий момент М в сечении с абсциссой х связан с углом поворота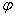 
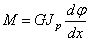
дифференциальной зависимостью, аналогичной (173):
, (186)
где Jp-полярный момент инерции поперечного сечения.
В сечении, расположенном на расстоянии dx , крутящий момент равен (рис.69,б):
.
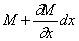
Обозначая через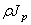 
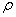
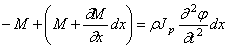
(где — плотность материала вала) интенсивность момента инерции массы вала относительно его оси (т.е. момент инерции единицы длины), уравнение движения элементарного участка вала можно записать так:
,
или подобно (174):
.
Подставляя сюда выражение (186), при Jp=const получим, аналогично (175):
, (187)
.
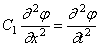
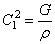
Общее решение уравнения (187), как и уравнения (175), имеет вид
,
(188)
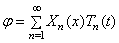
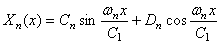
Собственные частоты и собственные функции при этом определяются конкретными граничными условиями.
В основных случаях закрепления концов аналогично случаю продольных колебаний получим
а) закрепленный конец ( 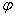=0): Х=0;
б) свободный конец (М=0): Х’=0;
в) упругозакрепленный левый конец: СоХ=GJpX ‘ ( Со-коэффициент жёсткости);
г) упругозакрепленный правый конец: — СоХ=GJpX ‘;
д ) диск на левом конце: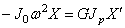 
(Jo-момент инерции диска относительно оси стержня);
е) диск на правом конце: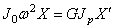 
.
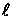
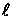
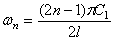
Если вал закреплён на левом конце (х=0), а правый конец ( х= ) свободен, то Х=0 при х=0 и Х’=0 при x= ; собственные частоты определяются аналогично (185):
(n=1,2,…).
Если левый конец закреплён, а на правом конце имеется диск, получим трансцендентное уравнение:
.
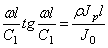
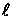
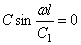
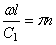
Если оба конца вала закреплены, то граничные условия будут X=0 при х=0 и х= . В этом случае из (188) получим
; D=0,
(n=1,2,…),
отсюда находим собственные частоты:
.
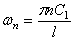
Если левый конец вала свободен, а на правом конце имеется диск, то X’=0 при х=0 ; Jo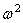 
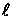
X=GJpX ‘ при х= .
При помощи (188) находим
С=0;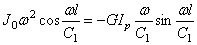 
,
или трансцендентное частотное уравнение:
.
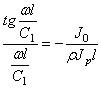
6.3.Изгибные колебания балок
6.3.1.Основное уравнение
Из курса сопротивления материалов известны дифференциальные зависимости при изгибе балок:
; (189)
, (190)
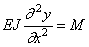
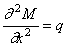
где EJ — жёсткость при изгибе; y=y ( x , t ) — прогиб; M=M( x , t ) — изгибающий момент; q — интенсивность распределённой нагрузки.
Объединяя (189) и (190), получим
. (191)
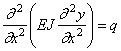
В задаче о свободных колебаниях нагрузкой для упругого скелета являются распределённые силы инерции:
,
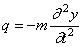
где m — интенсивность массы балки (масса единицы длины), и уравнение (191) принимает вид
.
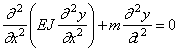
В частном случае постоянного поперечного сечения, когда EJ = const , m = const , имеем:
. (192)
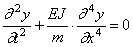
Для решения уравнения (192) полагаем, как и выше,
y = X ( x ) × T ( t ). (193)
Подставляя (193) в (192), приходим к уравнению:
.
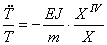
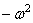
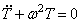
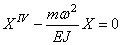
Для тождественного выполнения этого равенства необходимо, чтобы каждая из частей равенства была постоянной. Обозначая эту постоянную через , получим два уравнения:
; (194)
. (195)
Первое уравнение указывает на то, что движение носит колебательный характер с частотой .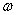
Второе уравнение определяет форму колебаний. Решение уравнения (195) содержит четыре постоянных и имеет вид
,
. (196)
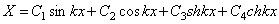
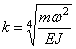
Удобно использовать вариант записи общего решения, предложенный А.Н.Крыловым:
, (197)
(198)
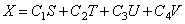
представляют собой функции А.Н.Крылова.
Обратим внимание на то, что S=1, T=U=V=0 при x=0. Функции S,T,U,V связаны между собой следующим образом:
(199)
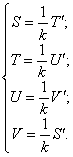
Поэтому производные выражения (197) записываются в виде
(200)
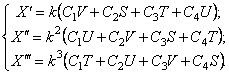
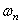
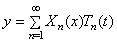
В задачах рассматриваемого класса число собственных частот бесконечно велико; каждой из них отвечает своя функция времени Tn и своя фундаментальная функция Xn . Общее решение получится путём наложения частных решений вида (193)
. (201)
Для определения собственных частот и формул необходимо рассмотреть граничные условия.
6.3.2. Граничные условия
Для каждого конца стержня можно указать два граничных условия .
Свободный конец стержня (рис. 70,а). Нулю равны поперечная сила Q=EJX»’T и изгибающий момент M=EJX»T. Поэтому граничные условия имеют вид
Шарнирно-опёртый конец стержня (рис.70,б). Нулю равны прогиб y=XT и изгибающий момент M=EJX»T. Следовательно, граничные условия таковы:
Защемленный конец (рис.70,в). Нулю равны прогиб y=XT и угол поворота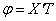 
. Граничные условия:
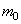
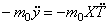
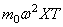
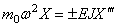
На конце стержня имеется точечный груз массы (рис.70,г). Его сила инерции 
может быть при помощи уравнения (194) записана так: 
; она должна быть равна поперечной силе Q=EJX»’T , поэтому граничные условия принимают вид
; X»=0 . (205)
В первом условии знак плюс принимается в случае, когда точечный груз связан с левым концом стержня, и знак минус, когда он связан с правым концом стержня. Второе условие вытекает из отсутствия изгибающего момента .
Упруго-опертый конец стержня (рис.70,д). Здесь изгибающий момент равен нулю, а поперечная сила Q=EJX»’T равна реакции опоры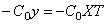 
(Co-коэффициент жёсткости опоры).
X»=0 ;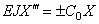 
(206)
(знак минус принимается в случае, когда упругая опора является левой, и знак плюс, когда она является правой).
6.3.3. Частотное уравнение и собственные формы
Развёрнутая запись граничных условий приводит к однородным уравнениям относительно постоянных C1, C2, C3, C4.
Чтобы эти постоянные не равнялись нулю, должен равняться нулю определитель, составленный из коэффициентов системы; это приводит к частотному уравнению. При этих операциях выясняются соотношения между C1, C2, C3, C4, т.е. определяются собственные формы колебаний (с точностью до постоянного множителя).
Проследим составление частотных уравнений на примерах.
Для балки с шарнирно-опёртыми концами согласно (203) имеем следующие граничные условия: X=0; X»=0 при x=0 и x= 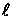. При помощи (197)-(200) получим из первых двух условий: C1=C3=0. Два оставшихся условия можно записать в виде
Чтобы C2 и C4 не были равны нулю, необходимо равенство нулю определителя:
.
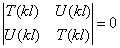
Таким образом, частотное уравнение имеет вид
.
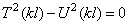
Подставляя выражения T и U, получим
.
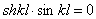
Так как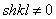 
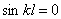
, то окончательно частотное уравнение записывается так:
. (207)
Корни этого уравнения:
, ( n =1,2,3. ).
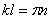
Учитывая (196), получим
. (208)
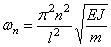
Перейдём к определению собственных форм. Из записанных выше однородных уравнений вытекает следующее соотношение между постоянными C2 и C4:
.
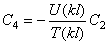
Следовательно, (197) приобретает вид
Согласно (207), имеем
, (209)
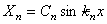
где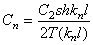 
— новая постоянная, значение которой остаётся неопределённым, пока не введены в рассмотрение начальные условия.
6.3.4. Определение движения по начальным условиям
Если требуется определить движение, следующее после начального возмущения, то необходимо указать для всех точек балки как начальные смещения, так и начальные скорости:
(210)
и использовать свойство ортогональности собственных форм:
.
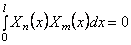
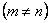
Общее решение (201) запишем так:
. (211)
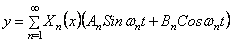
Скорость определяется выражением
. (212)
Подставляя в правые части уравнений (211) и (212) 
, а в левые части — предполагаемые известными начальные смещения и скорости, получим
.
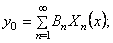
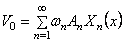
Умножая эти выражения на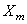 
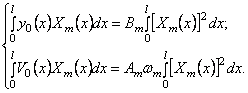
и интегрируя по всей длине, имеем
(213)
Бесконечные суммы в правых частях исчезли вследствие свойства ортогональности. Из (213) следуют формулы для постоянных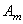 
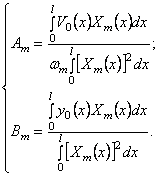
и 
(214)
Теперь эти результаты нужно подставить в решение (211).
Снова подчеркнём, что выбор масштаба собственных форм несущественен. Если, например, в выражении собственной формы (209) принять вместо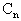 
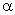
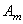
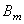
величину в 
раз большую, то (214) дадут результаты в 
раз меньшие; после подстановки в решение (211) эти различия компенсируют друг друга. Тем не менее часто пользуются нормированными собственными функциями, выбирая их масштаб таким, чтобы знаменатели выражений (214) равнялись единице, что упрощает выражения и .
6.3.5. Влияние постоянной продольной силы
Рассмотрим случай, когда колеблющаяся балка испытывает действие продольной силы N , величина которой не меняется в процессе колебаний. В этом случае уравнение статического изгиба усложняется и приобретает вид (при условии, что сжимающая сила считается положительной)
.
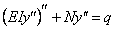
Полагая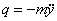 
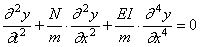
и считая жёсткость постоянной, получаем уравнение свободных колебаний
. (215)
Принимаем по-прежнему частное решение в виде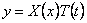 
.
Тогда уравнение (215) распадается на два уравнения:
Первое уравнение выражает колебательный характер решения, второе определяет форму колебаний, а также позволяет найти частоты. Перепишем его таким образом:
(216)
где K определяется формулой (196), а
. (217)
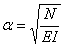
Решение уравнения (216) имеет вид
Рассмотрим случай, когда оба конца стержня имеют шарнирные опоры. Условия на левом конце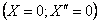 
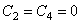
дают 
. Удовлетворяя те же условия на правом конце, получим
Приравнивая нулю определитель, составленный из коэффициентов при величинах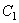 
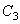
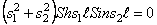
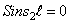
и 
, приходим к уравнению
,
. (218)
Корни этого частотного уравнения:
.
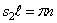
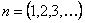
Следовательно, собственная частота определится из уравнения
.
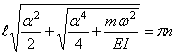
Отсюда при учёте (217) находим
. (219)
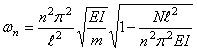
При растяжении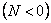 
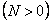
частота увеличивается, при сжатии 
уменьшается. Когда сжимающая сила N приближается к критическому значению, корень стремится к нулю.
6.3.6. Влияние цепных усилий
Ранее продольная сила считалась заданной и не зависящей от перемещений системы. В некоторых практических задачах сопровождающая процесс поперечных колебаний продольная сила возникает вследствие изгиба балки и носит характер реакции опоры. Рассмотрим, например, балку на двух шарнирно-неподвижных опорах. При её изгибе возникают горизонтальные реакции опор, вызывающие растяжение балки; соответствующее горизонтальное усилие принято называть цепным усилием. Если балка совершает поперечные колебания, то цепное усилие будет изменяться во времени.
Если в мгновение t прогибы балки определяются функцией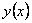 
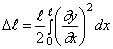
, то удлинение оси можно найти по формуле
.
Соответствующее цепное усилие найдём при помощи закона Гука
.
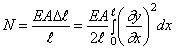
Подставим этот результат в (215) вместо продольной силы N (с учётом знака)
. (220)
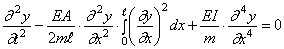
Полученное нелинейное интегродифференциальное уравнение упрощается при помощи подстановки
, (221)
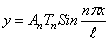
где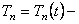 
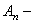
безразмерная функция времени, максимальное значение которой можно положить равным любому числу, например, единице; 
амплитуда колебаний.
Подставляя (221) в (220), получим обыкновенное дифференциальное уравнение
, (222)
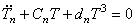
коэффициенты которого имеют следующие значения:
; 
.
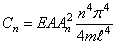
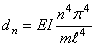
Дифференциальное уравнение (222) является нелинейным, следовательно, частота свободных колебаний зависит от их амплитуды.
Точное решение для 
частоты поперечных колебаний 
имеет вид
,
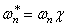
где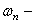 
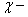
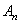
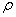
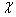
частота поперечных колебаний, вычисленная без учёта цепных усилий; 
поправочный коэффициент, зависящий от отношения амплитуды колебаний 
к радиусу инерции поперечного сечения ; величина 
приводится в справочной литературе.
При соизмеримости амплитуды и радиуса инерции поперечного сечения поправка к частоте становится значительной. Если, например, амплитуда колебаний стержня круглого сечения равна его диаметру, то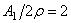 
, и частота почти в два раза больше, чем в случае свободного смещения опор.
Случай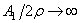 
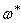
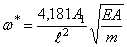
соответствует нулевому значению радиуса инерции, когда изгибная жёсткость балки исчезающе мала — струна. При этом формула для 
даёт неопределённость. Раскрывая эту неопределённость, получим формулу для частоты колебаний струны
.
Эта формула относится к случаю, когда в положении равновесия натяжение равно нулю. Часто задачу о колебаниях струны ставят в других предположениях: считают, что перемещения малы, а растягивающая сила задана и остаётся неизменной в процессе колебаний.
При этом формула для частоты имеет вид
,
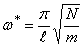
где N — постоянная растягивающая сила.
6.4. Влияние вязкого трения
Ранее предполагалось, что материал стержней идеально упругий и трение отсутствует. Рассмотрим влияние внутреннего трения, считая, что оно является вязким; тогда связь напряжений с деформациями описывается соотношениями
; 
. (223)
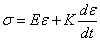
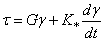
Пусть стержень с распределёнными параметрами совершает свободные продольные колебания. В этом случае продольная сила запишется в виде
. (224)
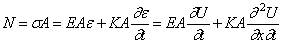
Из уравнения движения элемента стержня было получено соотношение (174)
.
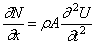
Подставляя сюда (224), приходим к основному дифференциальному уравнению
, (225)
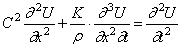
которое отличается от (175) вторым слагаемым, выражающим влияние сил вязкого трения.
Следуя методу Фурье, ищем решение уравнения (225) в виде
, (226)
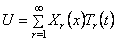
где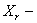 
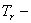
функция только координаты x , а 
функция только времени t .
При этом каждый член ряда должен удовлетворять граничным условиям задачи, а вся сумма — также и начальным условиям. Подставляя (226) в (225) и требуя, чтобы равенство удовлетворялось для любого номера r , получим
, (227)
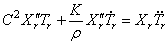
где штрихи обозначают дифференцирование по координате x , а точки — дифференцирование по времени t .
Разделив (227) на произведение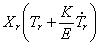 
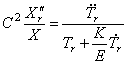
, приходим к равенству
, (228)
левая часть, которого может зависеть только от координаты x , а правая — только от времени t . Для тождественного выполнения равенства (228) необходимо, чтобы обе части были равны одной и той же постоянной, которую обозначим через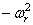 
.
Из этого следуют уравнения
(229)
. (230)
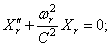
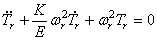
Уравнение (229) не зависит от коэффициента вязкости K и, в частности, остаётся таким же в случае идеально упругой системы, когда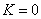 
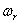
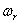
. Поэтому числа 
полностью совпадают с найденными ранее; однако, как будет показано ниже, величина даёт лишь приближённое значение собственной частоты. Отметим, что собственные формы совершенно не зависят от вязких свойств стержня, т.е. формы свободных затухающих колебаний совпадают с формами свободных незатухающих колебаний.
Теперь перейдём к уравнению (230), описывающему процесс затухающих колебаний; его решение имеет вид
, (231)
; (232)
. (233)
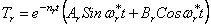
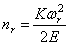
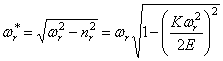
Выражение (232) определяет темп затухания, а (233) — частоту колебаний.
Таким образом, полное решение уравнения задачи
. (234)
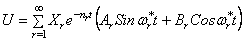
Постоянные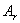 
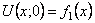
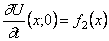
и 
всегда можно найти по заданным начальным условиям. Пусть начальные смещения и начальные скорости всех сечений стержня заданы следующим образом:
; 
, (235)
где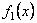 
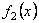
и 
— известные функции.
Тогда при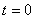 
, согласно (211) и (212), имеем
умножая обе части этих равенств на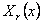 
и интегрируя в пределах всей длины стержня, получим
(236)
Соответственно условию ортогональности собственных форм все остальные слагаемые, входящие в правые части этих равенств, обращаются в нуль. Теперь из равенств (236) легко найти 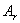и для любого номера r .
Рассматривая (232) и (234), заметим, что чем выше номер формы колебаний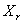 
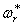
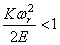
, тем быстрее её затухание. Кроме того, слагаемые, входящие в (234), описывают затухающие колебания, если 
есть действительное число. Из (233) видно, что это имеет место лишь для нескольких начальных значений r , пока выполняется неравенство
. (237)
При достаточно больших значениях r неравенство (237) нарушается и величина 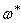становится мнимой. При этом соответствующие члены общего решения (234) уже не будут описывать затухающие колебания, но будут представлять апериодическое затухающее движение. Другими словами, колебания, в обычном смысле слова, выражает только некоторая конечная часть суммы (234).
Все эти качественные выводы относятся не только к случаю продольных колебаний, но и к случаям крутильных и изгибных колебаний.
6.5. Колебания стержней переменного сечения
В тех случаях, когда распределённая масса и сечение стержня переменны по его длине, следует вместо уравнения продольных колебаний (175) исходить из уравнения
. (238)
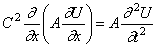
Уравнение крутильных колебаний (187) должно быть заменено уравнением
, (239)
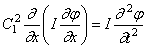
а уравнение поперечных колебаний (192) – уравнением
. (240)
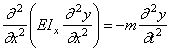
Уравнения (238)-(240) при помощи однотипных подстановок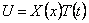 
; 
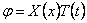
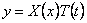
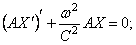
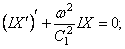
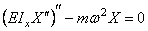
; можно привести к обыкновенным дифференциальным уравнениям для функции 
(241)
(242)
(243)
и одному однотипному уравнению для функции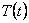 
.
Уравнения (241)-(243) в отличие от уравнений, решённых выше, имеют переменные коэффициенты.
Замкнутую форму решений можно получить лишь в отдельных случаях, когда переменные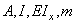 
определены специальными зависимостями. В общем случае неизбежен переход к приближённым методам. В частности, возможен путь, основанный на сосредоточении распределённой массы в ряде точек по длине стержня, после чего система сохраняет лишь конечное число степеней свободы, равное числу точек приведения. Используются также различные варианты вариационного метода и некоторые другие приближённые методы, о которых речь пойдёт ниже.
6.6. Колебания круговых колец
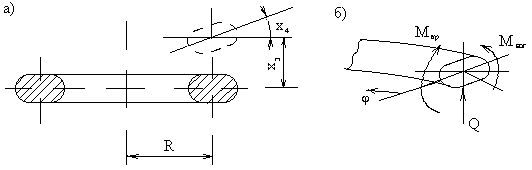
6.6.1. Колебания в плоскости кольца
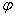
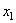
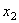
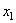
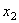
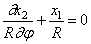
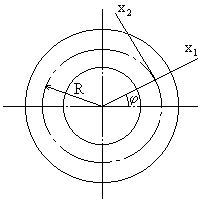
Рассмотрим круговой брус малой кривизны постоянного сечения с радиусом R осевой линии (рис.71,а). Будем считать груз нерастяжимым. Перемещение центра тяжести поперечного сечения, зафиксированного угловой координатой , можно разложить на радиальный и окружной компоненты — соответственно 
и 
. Из условия нерастяжимости оси бруса следует, что перемещения и связаны зависимостью:
. (244)
Угол поворота поперечного сечения бруса в процессе движения определяется формулой
. (245)
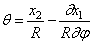
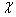
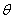
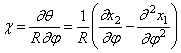
Изменение кривизны бруса равно производной от 
по дуге:
. (246)
Изгибающий момент в поперечном сечении кольца:
. (247)
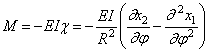
Теперь составим уравнение движения элемента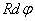 
бруса (рис.71,б).
Помимо перечисленных сил, на элемент действует также сила инерции:
,
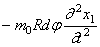
где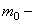 
масса единицы длины бруса.
Проектируя приложенные к элементу силы на радиус, получим
. (248)
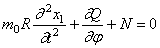
Равенство нулю суммы проекций всех сил на направление касательной приводит к уравнению:
. (249)
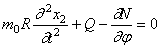
Уравнение моментов имеет вид
. (250)
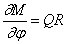
Исключим из (248) и (249) нормальную силу N , а поперечную силу Q заменим её значением из (250):
. (251)
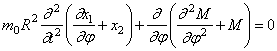
Подставляя сюда значение M из (247), получим уравнение движения в перемещениях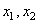 
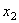
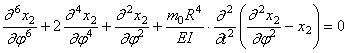
, и, наконец, исключая один из компонентов перемещения, с помощью условия нерастяжимости (244) придём к уравнению, в которое входит единственная переменная :
. (252)
Решение уравнения движения (252) будем искать в виде
; 
.
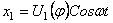
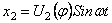
При этом для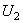 
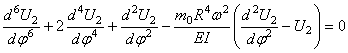
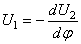
получается обыкновенное дифференциальное уравнение
, (253)
.
Согласно общим правилам решения дифференциальных уравнений, следует найти общее решение уравнения (253), включающее шесть постоянных, и подчинить его граничным условиям. На каждом конце бруса должны быть равны нулю либо компоненты перемещений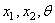 
, либо соответствующие им внутренние силы. Равенство нулю определителя системы, выражающей граничные условия, приводит к частотному уравнению.
Для замкнутого кольца граничные условия заменяются условиями периодичности, которые выполняются, если принять
; 
. (254)
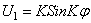
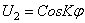
Подставляя (254) в (253), устанавливаем, что последнее удовлетворяется тождественно, если
. (255)
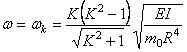
Формула (255) определяет частоты собственных колебаний кольца в своей плоскости. Значению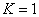 
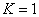
соответствует нулевая частота, так как при формулы (254) описывают смещение кольца как жёсткого тела.
6.6.2. Колебания, перпендикулярные плоскости кольца
В этом случае положение поперечного сечения кольца в процессе движения характеризуется смещением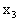 
его центра тяжести из плоскости кольца и углом поворота сечения х4 (рис.72,а). В поперечном сечении кольца возникают изгибающие и крутящие моменты (рис.72,б), а также поперечная сила, перпендикулярная плоскости кольца.
Установим зависимость моментов от перемещений. Так как задача линейная, то рассмотрим сначала силовые факторы, связанные со смещением х3, а затем — с х4.
Если х3 постоянно по длине окружности, то кольцо смещается как жёсткое целое, и внутренние силы не возникнут. Если х3 изменяется в зависимости от центрального угла по линейному закону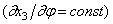 
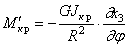
, то ось бруса превращается в винтовую линию, т.е. брус деформируется подобно витку пружины при растяжении. Известно, что в этом случае в поперечных сечениях возникает крутящий момент
,
где GJ кр — крутильная жёсткость бруса.
Если при этом отлична от нуля и вторая производная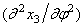 
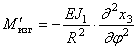
, то меняется кривизна бруса и возникает изгибающий момент
,
где J 1 — момент инерции сечения относительно центральной оси, лежащей в плоскости кривизны.
Найдём силовые факторы, связанные с поворотом х4. Если х4 постоянно, то происходит осесимметричный изгиб кольца, причём в его сечениях возникает изгибающий момент
.
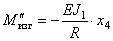
При переменном по длине повороте х4 соседние сечения поворачиваются друг относительно друга и возникает крутящий момент
.
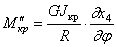
Суммируя силовые факторы, связанные с перемещениями х3 и х4, ,получаем
(256)
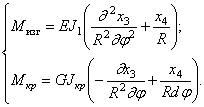
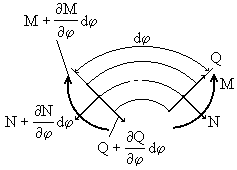
Составим уравнение движения элемента Rd 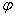бруса (рис.73).
Будем пренебрегать инерцией поворота элемента вокруг своей оси.
Условие динамического равновесия в направлении нормали к плоскости кольца приводит к уравнению:
. (257)
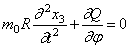
Сумма моментов относительно нормали к оси элемента:
. (258)
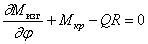
Сумма моментов относительно касательной к оси элемента:
. (259)
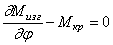
Исключая поперечную силу из (257) и (258) и заменяя моменты в полученном уравнении и уравнении (259) их значениями (256), приходим к системе уравнений, в которую входят только перемещения х3 и х4:
(260)
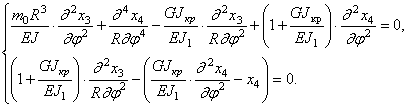
Ограничиваясь исследованием собственных колебаний замкнутого кольца, решение уравнений (260) можно представить в виде
x3 = Acosk j × cos w t , x4 = Bcosk j × cos w t . (261)
Подставляя значения (261) в уравнение движения (260), получим
(262)
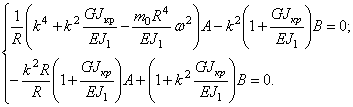
Из равенства нулю определителя этой системы получим частотное уравнение, корни которого — собственные частоты — таковы:
(263)
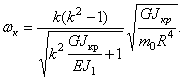
Наименьшая отличная от нуля частота соответствует k =2.
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
http://vicaref.narod.ru/PDE/index2.htm
http://www.detalmach.ru/lectdinamika6.htm