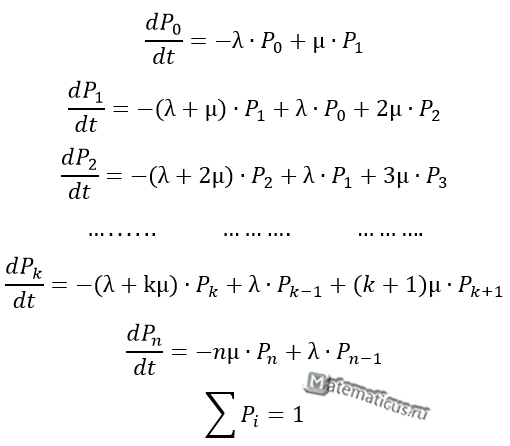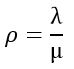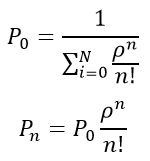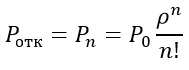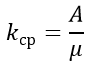Уравнения колмогорова для многоканальной смо с отказами

Многоканальная СМО с отказами

Многоканальная СМО (система массового обслуживания) с отказами, означает, что СМО состоит из нескольких каналов обслуживания и если все каналы заняты, то транзакт (заявка) покидает систему обслуживания.

Граф состояний многоканальной СМО с отказами

S₀ – все каналы свободны;

S₁ – один канал занят, остальные свободны;

S₂ – два канала заняты, остальные свободны;

S_k – занято k каналов, остальные свободны;

S_n – заняты все n каналов.

Вероятностные состояния каналов обслуживания можно определить через дифференциальные уравнения Колмогорова:

Формула интенсивность потока заявок ρ:

ρ – интенсивность потока заявок;

λ – поток заявок;

μ – поток обслуживания.

Формула Эрланга имеет вид:

Формула вероятности отказа P_отк для многоканальной СМО с отказами:

Относительная пропускная способность для многоканальной СМО с отказами q определяется по формуле:

q=(1-P) n

Абсолютная пропускная способность A находится по формуле:

A=λq

Формула для определения среднего числа занятых каналов k_ср:

Многоканальная СМО с отказами

Процесс обслуживания является процессом гибели и размножения. Уравнения Колмогорова для этого частного случая будут иметь следующий вид:

(7.25)
Уравнения (7.25) называются уравнениями Эрланга.
Для того, чтобы найти значения вероятностей состояний Р₀, Р₁, …, Р_n, необходимо определить начальные условия:
– Р₀(0) = 1, т. е. на входе системы стоит заявка;
– Р₁(0) = Р₂(0) = … = Р_n(0) = 0, т. е. в начальный момент времени система свободна.
Проинтегрировав систему дифференциальных уравнений (7.25), получим значения вероятностей состояний Р₀(t), Р₁(t), … Р_n(t).
Но гораздо больше нас интересуют предельные вероятности состояний. При t → ∞ и по формуле, полученной при рассмотрении процесса гибели и размножения, получим решение системы уравнений (7.25):

(7.26)
В этих формулах отношение интенсивности λ / μ к потоку заявок удобно обозначить ρ. Эту величину называют приведенной интенсивностью потока заявок, то есть среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

С учетом сделанных обозначений система уравнений (7.26) примет следующий вид:

.
Вероятность того, что заявка будет принята к обслуживанию:

Q = 1 – Р_отк ,
где Q – средняя доля поступивших заявок, обслуживаемых системой, или среднее число заявок обслуженных СМО в единицу времени, отнесенное к среднему числу поступивших за это время заявок:

A=λ·Q=λ·(1-P_отк)
Кроме того, одной из важнейших характеристик СМО с отказами является среднее число занятых каналов. В n-канальной СМО с отказами это число совпадает со средним числом заявок, находящихся в СМО.
Среднее число заявок k можно вычислить непосредственно через вероятности состояний Р ₀, Р ₁, … , Р _n:

k = 0·P₀+1·P₁+ . + n·P_n,
т. е. находим математическое ожидание дискретной случайной величины, которая принимает значение от 0 до n с вероятностями Р₀, Р₁, …, Р_n.
Еще проще выразить величину k через абсолютную пропускную способность СМО, т.е. А . Величина А – среднее число заявок, которые обслуживаются системой в единицу времени. Один занятый канал обслуживает за единицу времени μ заявок, тогда среднее число занятых каналов

СМО с отказами: определения и формулы

В качестве показателей эффективности СМО с отказами будем рассматривать:

1) — абсолютную пропускную способность СМО , т.е. среднее число заявок, обслуживаемых в единицу времени;

2) — относительную пропускную способность , т.е. среднюю долю пришедших заявок, обслуживаемых системой;

3) — вероятность отказа , т.е. того, что заявка покинет СМО необслуженной;

4) — среднее число занятых каналов (для многоканальной системы).

Одноканальная система (СМО) с отказами

Рассмотрим задачу. Имеется один канал, на который поступает поток заявок с интенсивностью . Поток обслуживании имеет интенсивность . Найти предельные вероятности состояний системы и показатели ее эффективности.

Примечание. Здесь и в дальнейшем предполагается, что все потоки событий, переводящие СМО из состояния в состояние, будут простейшими. К ним относится и поток обслуживании — поток заявок, обслуживаемых одним непрерывно занятым каналом. Среднее время обслуживания обратно по величине интенсивности , т.е. .

Система (СМО) имеет два состояния: — канал свободен, — канал занят. Размеченный граф состояний представлен на рис. 6.

В предельном, стационарном режиме система алгебраических уравнений для вероятностей состояний имеет вид (см. выше правило составления таких уравнений)

т.е. система вырождается в одно уравнение. Учитывая нормировочное условие , найдем из (18) предельные вероятности состояний

которые выражают среднее относительное время пребывания системы в состоянии (когда канал свободен) и (когда канал занят), т.е. определяют соответственно относительную пропускную способность системы и вероятность отказа

Абсолютную пропускную способность найдем, умножив относительную пропускную способность на интенсивность потока отказов

Пример 5. Известно, что заявки на телефонные переговоры в телевизионном ателье поступают с интенсивностью , равной 90 заявок в час, а средняя продолжительность разговора по телефону мин. Определить показатели эффективности работы СМО (телефонной связи) при наличии одного телефонного номера.

Решение. Имеем (1/ч), мин. Интенсивность потока обслуживании (1/мин) (1/ч). По (20) относительная пропускная способность СМО , т.е. в среднем только 25% поступающих заявок осуществят переговоры по телефону. Соответственно вероятность отказа в обслуживании составит (см. (21)). Абсолютная пропускная способность СМО по (29) , т.е. в среднем в час будут обслужены 22,5 заявки на переговоры. Очевидно, что при наличии только одного телефонного номера СМО будет плохо справляться с потоком заявок.

Многоканальная система (СМО) с отказами.

Рассмотрим классическую задачу Эрланга . Имеется каналов, на которые поступает поток заявок с интенсивностью . Поток обслуживании имеет интенсивность . Найти предельные вероятности состояний системы и показатели ее эффективности.

Система (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): , где — состояние системы, когда в ней находится заявок, т.е. занято каналов.

Граф состояний СМО соответствует процессу гибели и размножения и показан на рис. 7.

Поток заявок последовательно переводит систему из любого левого состояния в соседнее правое с одной и той же интенсивностью . Интенсивность же потока обслуживании, переводящих систему из любого правого состояния в соседнее левое состояние, постоянно меняется в зависимости от состояния. Действительно, если СМО находится в состоянии (два канала заняты), то она может перейти в состояние (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживании будет . Аналогично суммарный поток обслуживании, переводящий СМО из состояния (три канала заняты) в , будет иметь интенсивность , т.е. может освободиться любой из трех каналов и т.д.

В формуле (16) для схемы гибели и размножения получим для предельной вероятности состояния

где члены разложения , будут представлять собой коэффициенты при в выражениях для предельных вероятностей . Величина

называется приведенной интенсивностью потока заявок или интенсивностью нагрузки канала . Она выражает среднее число заявок, приходящее за среднее время обслуживания одной заявки. Теперь

Формулы (25) и (26) для предельных вероятностей получили названия формул Эрланга в честь основателя теории массового обслуживания.

Вероятность отказа СМО есть предельная вероятность того, что все я каналов системы будут заняты, т.е.

Относительная пропускная способность — вероятность того, что заявка будет обслужена:

Абсолютная пропускная способность:

Среднее число занятых каналов есть математическое ожидание числа занятых каналов:

где — предельные вероятности состояний, определяемых по формулам (25), (26).

Однако среднее число занятых каналов можно найти проще, если учесть, что абсолютная пропускная способность системы есть не что иное, как интенсивность потока обслуженных системой заявок (в единицу времени). Так как каждый занятый канал обслуживает в среднем заявок (в единицу времени), то среднее число занятых каналов

Пример 6. В условиях примера 5 определить оптимальное число телефонных номеров в телевизионном ателье, если условием оптимальности считать удовлетворение в среднем из каждых 100 заявок не менее 90 заявок на переговоры.

Решение. Интенсивность нагрузки канала по формуле (25) , т.е. за время среднего (по продолжительности) телефонного разговора мин. поступает в среднем 3 заявки на переговоры.

Будем постепенно увеличивать число каналов (телефонных номеров) и определим по формулам (25), (28), (29) для получаемой n-канальной СМО характеристики обслуживания. Например, при имеем

Значение характеристик СМО сведем в табл. 1.

По условию оптимальности , следовательно, в телевизионном ателье необходимо установить 5 телефонных номеров (в этом случае — см. табл. 1). При этом в час будут обслуживаться в среднем 80 заявок , а среднее число занятых телефонных номеров (каналов) по формуле (30) .

Пример 7. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 3 ч. Интенсивность потока заявок 0,25 (1/ч). Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра.

Решение. По условию (1/ч), =3 (ч). Интенсивность потока обслуживании . Интенсивность нагрузки ЭВМ по формуле (24) . Найдем предельные вероятности состояний:

т.е. в стационарном режиме работы вычислительного центра в среднем 47,6% времени нет ни одной заявки, 35,7% — имеется одна заявка (занята одна ЭВМ), 13,4% — две заявки (две ЭВМ), 3,3% времени — три заявки (заняты три ЭВМ).

Вероятность отказа (когда заняты все три ЭВМ), таким образом, .

По формуле (28) относительная пропускная способность центра , т.е. в среднем из каждых 100 заявок вычислительный центр обслуживает 96,7 заявок.

По формуле (29) абсолютная пропускная способность центра , т.е. в один час в среднем обслуживается. 0,242 заявки.

По формуле (30) среднее число занятых ЭВМ , т.е. каждая из трех ЭВМ будет занята обслуживанием заявок в среднем лишь на .

При оценке эффективности работы вычислительного центра необходимо сопоставить доходы от выполнения заявок с потерями от простоя дорогостоящих ЭВМ (с одной стороны, у нас высокая пропускная способность СМО, а с другой стороны — значительный простой каналов обслуживания) и выбрать компромиссное решение.