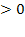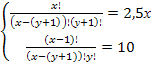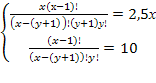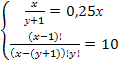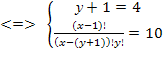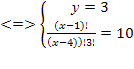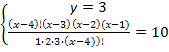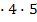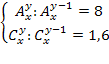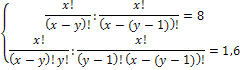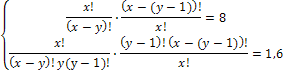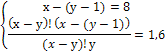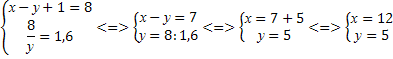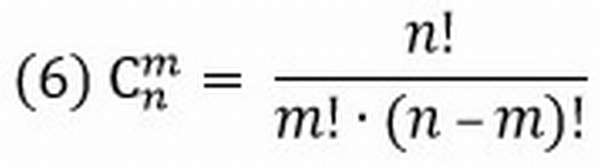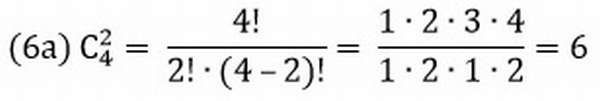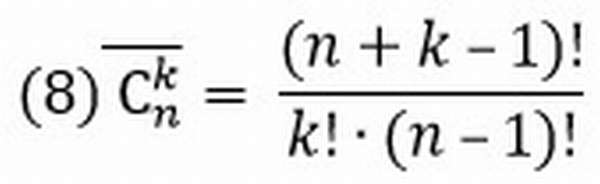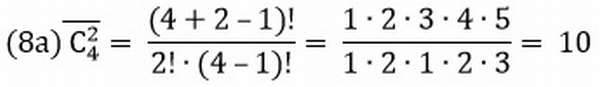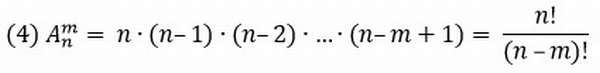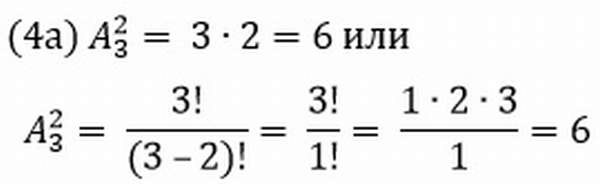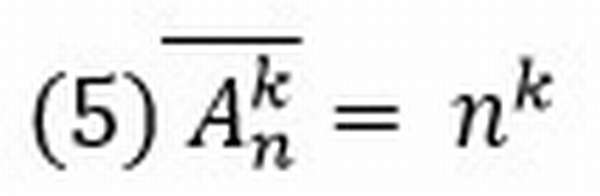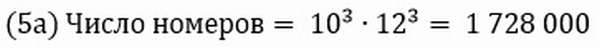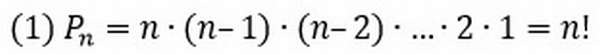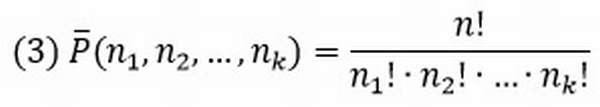Математика — онлайн помощь
Рассмотрим множество, состоящее из n различных элементов. Требуется выбрать из них какие-нибудь k элементов и расположить эти k элементов в каком-либо порядке. Такие упорядоченные последовательности называются размещениями из n элементов по k элементов (упорядоченные – следовательно, последовательности <1,2>и <2,1>— различные размещения).
Если в последовательности нет одинаковых элементов, то говорят о размещении без повторений. Их количество
Если в последовательности допускается наличие одинаковых элементов, то говорят о размещении с повторениями. Их количество
Любое подмножество (неупорядоченное), состоящее из k элементов, называется сочетанием из n элементов по k элементов.
Различные сочетания отличаются друг от друга только самими входящими в них элементами, порядок их следования безразличен, т.е. по условию задачи подмножества <1,2>и <2,1>не различны (соединены).
Число сочетаний без повторений
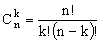
Число сочетаний с повторениями
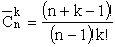
Количество способов переставить элементов в заданном множестве (количество перестановок) вычисляется по формуле
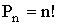
При решении простейших комбинаторных задач можно использовать следующую таблицу, определяющую число множеств, состоящих из k элементов, отбираемых из множества, содержащего n элементов
| Выбор | Неупорядоченный | Упорядоченный |
| Без повтора | 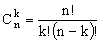 | 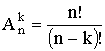 |
| С повтором | 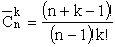 | 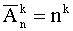 |
Рассмотрим разницу между сочетаниями, размещениями с повторениями, без повторений на следующих примерах.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.1 В коробке 6 шаров, пронумерованных от 1 до 6. Из коробки вынимаются друг за другом 3 шара и в этом же порядке записывают полученные цифры. Сколько трехзначных чисел можно таким образом записать?
Решение: По условию задачи подмножества <1;2;3>и <3;1;2>– различные. Повторов в подмножестве быть не может, так как шары не возвращаются в коробку.
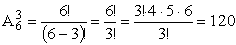
ПРИМЕР 13.2.2. В коробке 6 шаров пронумерованных от 1 до 6. Из коробки вынимаются 3 шара и записывают число в порядке возрастания цифр. Сколько трехзначных чисел можно таким образом записать?
Решение: По условию задачи подмножества <1;2;3>и <3;2;1>дают число 123, т.е. не являются различными.
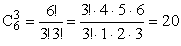
ПРИМЕР 13.2.3. Условие задачи 2.1 (шары возвращаются в коробку)
Решение: 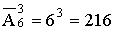
ПРИМЕР 13.2.4. Условие задачи 2.2 (шары возвращаются в коробку)
Решение: 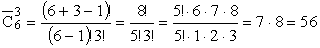
ПРИМЕР 13.2.5. Сколько различных перестановок можно составить из букв слова «комар»?
Решение: 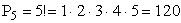
ПРИМЕР 13.2.6. Сколько различных перестановок можно составить из букв слова «задача»?
Решение: Если бы все шесть букв слова были различны, то число перестановок было бы 6! Но буква «а» встречается в данном слове три раза, и перестановки только этих трех букв «а» не дают новых способов расположения букв. Поэтому число перестановок букв слова «задача» будет не 6!, а в 3! раза меньше, то есть 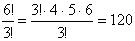
ПРИМЕР 13.2.7. В мастерской имеется материал 5 цветов. Поступил заказ на пошив флагов, состоящих из трех горизонтальных полос разного цвета каждый. Сколько таких различных флагов может сшить мастерская?

Решение: Флаги отличаются друг от друга как цветом полос, так и их порядком, поэтому разных флагов можно сделать 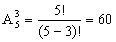
ПРИМЕР 13.2.8. Сколькими способами можно распределить 5 учеников по 3 параллельным классам?
Решение: Составим вспомогательную таблицу
| Номер ученика | |||||||||||||||||||||||||||||||||||||||||||
| Вариант класса | Таким образом, видно, что если для одного ученика существует 3 варианта выбора класса, то для всех 5 учеников существует ПРИМЕР 13.2.9. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом первый и второй том не стояли рядом? Решение: Произведем рассуждения “от обратного”. Тридцать томов на одной полке можно разместить 30! способами.
Если 1 и 2 тома должны стоять рядом, то число вариантов расстановки сокращается до
Тогда искомое число способов расстановки есть ПРИМЕР 13.2.10. Чемпионат, в котором участвуют 16 команд, проводится в два круга, т.е. каждая команда дважды встречается с любой другой. Определить, какое количество встреч следует провести. Решение: По условию задачи из 16 команд для каждой встречи требуется отобрать 2 команды. В данном случае отбор производится без повтора и порядок отбора не важен, т.е. число вариантов — ПРИМЕР 13.2.11. Автомобильная мастерская имеет для окраски 10 основных цветов. Сколькими способами можно окрасить автомобиль, если смешивать от 3 до 7 основных цветов? Решение: По условию задачи отбор цветов для окраски производится без повтора и порядок отбора не важен, т.е. число вариантов зависит лишь от числа отбираемых для окраски цветов —
ПРИМЕР 13.2.12. Турист прошел маршрут из пункта A в пункт B, из B в C и вернулся обратно. Сколько вариантов маршрута существует, если из пункта A в пункт B ведут 3 дороги, а из B в C — 4 и нельзя возвращаться той дорогой, по которой уже прошел? Решение: Составим схему. Из рисунка видно, что вариантов маршрута из А в B существует 3, и из B в C – 4, т.е. всего маршрутов На обратном пути вариантов маршрута из С в B существует 3 (один уже пройден), и из B в А – 2, т.е. всего возможных обратных маршрутов осталось ПРИМЕР 13.2.13. Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда по 6 человек, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант? Решение: Рассуждения произведем несколькими способами I способ) Первоначально 12 учеников разбивают на 2 группы по 6 человек. Это можно сделать Затем они могут распределиться по своим рядам согласно схеме
Поэтому всего способов распределения учеников будет II способ) Первоначально 12 учеников запускают в класс, указывая место, где каждый должен сидеть, например “второй ряд, третье место”. Так как посадочных мест также 12, то всего вариантов распределения 12! “I вариант – I ряд, II вариант – II ряд” “II вариант – I ряд, I вариант – II ряд”, Таким образом, всего способов распределения учеников будет По приведенным решениям видно, что результаты решений совпадают. ПРИМЕР 13.2.14. Сколько существует вариантов расположения шести гостей за круглым шестиместным столом? Решение: Эта задача имеет разные решения и, соответственно разные ответы – в зависимости от того, что понимать под различным расположением гостей за столом. Поэтому исследуем возможные варианты. Если считать, что нам важно, кто сидит на каком стуле, то это простая задача на перестановки и, следовательно, всего вариантов Если же важно не то, кто какой стул занял, а то, кто рядом с кем сидит, то требуется рассмотреть варианты взаимного расположения гостей. В таком случае, расположения гостей, получаемые одно из другого при повороте гостей вокруг стола, фактически являются одинаковыми (смотри рисунок). Очевидно, что для любого расположения гостей таких одинаковых вариантов, получаемых друг из друга поворотом, — шесть. Тогда общее число вариантов уменьшается в шесть раз и их остается В такой постановке вопроса общее число различных вариантов расположений гостей уменьшается вдвое и составляет 60. Отметим, что каждое решение будет считаться правильным при соответствующей постановке задачи. ПРИМЕР 13.2.15. Семнадцать студентов сдали экзамены по 4 предметам только на “хорошо” и “отлично”. Верно ли утверждение, что хотя бы у двух из них оценки по экзаменационным предметам совпадают? Решение: Очевидно, что в данном случае речь идет о возможных вариантах вида
Данный пример можно решить способом, изложенным в примере 13.1.8., и получить количество вариантов
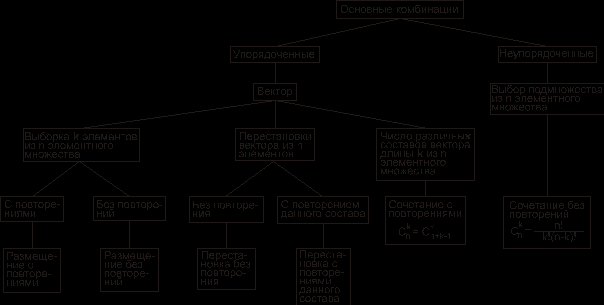
По “дереву решений” видно, что 16 студентов могут сдать экзамены только на “хорошо” и “отлично” так, что их результаты будут отличаться, но если студентов 17, хотя бы одно повторение обязательно будет. При решении задач комбинаторики используются следующие правила. Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B может быть выбран nспособами, то: Правило суммы: выбрать либо A, либо B можно m+n способами. Правило произведения. Пара объектов (A,B) в указанном порядке может быть выбрана Примеры и задачи для самостоятельного решенияРешить комбинаторную задачу. 13.2.1.1. В группе 25 студентов. Сколькими способами можно выбрать старосту, заместителя старосты и профорга? 13.2.1.2. В группе 25 студентов. Сколькими способами можно выбрать актив группы, состоящий из старосты, заместителя старосты и профорга? 13.2.1.3. Сколькими способами можно составить список из 10 человек? 13.2.1.4. Сколькими способами из 15 рабочих можно создать бригады по 5 человек в каждой? 13.2.1.5. Буквы азбуки Морзе образуются как последовательности точек и тире. Сколько букв можно составить, используя для кодировки каждой из букв: а) ровно 5 символов? б) не более пяти символов? 13.2.1.6. Кости для игры в домино метятся двумя цифрами. Кости симметричны, и поэтому порядок чисел не существенен. Сколько различных костей можно образовать, используя числа 0,1,2,3,4,5,6? 13.2.1.7. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти различных звуков? 13.2.1.8. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета? 13.2.1.9. В некоторых странах номера трамвайных маршрутов обозначаются двумя цветными фонарями. Какое количество различных маршрутов можно обозначить, если использовать фонари восьми цветов? 13.2.1.10. Команда компьютера записывается в виде набора из восьми цифровых знаков – нулей и единиц. Каково максимальное количество различных команд? 13.2.1.11. Десять групп занимаются в десяти расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы 1 и 2 находились бы в соседних аудиториях? 13.2.1.12. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу? 13.2.1.13. Замок открывается только в том случае, если набран определенный трехзначный номер. Попытка состоит в том, что набирают наугад три цифры из заданных пяти. Угадать номер удалось только на последней из всех возможных попыток. Сколько попыток предшествовало удачной? 13.2.1.14. Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр? 13.2.1.15. У одного студента есть 7 DVD дисков, а у другого – 9 дисков. Сколькими способами они могут обменять 3 диска одного на 3 диска другого? 13.2.1.16. На вершину горы ведут 7 дорог. Сколькими способами турист может два раза подняться на гору и спуститься с нее, если по одной и той же дороге нельзя проходить дважды? 13.2.1.17. У ювелира было 9 разных драгоценных камней: сапфир, рубин, топаз и т.д. Ювелир планировал изготовить браслет для часов, однако три камня было украдено. Насколько меньше вариантов браслета он может изготовить по сравнению с первоначальными планами? 13.2.1.18. В поезд метро на начальной станции вошли 10 пассажиров. Сколькими способами могут выйти все пассажиры на последующих 6 станциях? 13.2.1.19. За одним столом надо рассадить 5 мальчиков и 5 девочек так, чтобы не было двух рядом сидящих мальчиков и двух рядом сидящих девочек. Сколькими способами это можно сделать? 13.2.1.20. В классе 25 учеников. Верно ли утверждение, что, по крайней мере, у трех из них день рождения в один и тот же месяц? 13.2.1.21. На участке железной дороги расположено 25 станций с билетной кассой в каждой. Касса каждой станции продает билеты до любой другой станции, притом в обоих направлениях. Сколько различных вариантов билетов можно выдать на этом участке? 13.2.1.22. На официальном приеме 50 человек обменялись рукопожатиями. Сколько было сделано рукопожатий? 13.2.1.23. Сколько диагоналей у выпуклого двадцатиугольника? Уважаемые студенты Конспект урока на тему «Решение комбинаторных уравнений» (10 класс)Сочетаниями без повторений занимался еще великий Паскаль. Он предложил специальную таблицу значений сочетаний без повторений. Значения представлены в табл. которая называется треугольником Паскаля. Этот треугольник удивительно красив своей математической красотой, и в его числах можно при желании отыскать различные закономерности. Его можно представить несколько иначе – в виде [26]: равнобедренного треугольника (рис. 10). Рис. 10. Треугольник Паскаля Здесь каждое число, кроме единиц на боковых сторонах, является суммой двух чисел, стоящих над ним. Поэтому: (приводим к общему знаменателю) (выносим n ! за скобку в знаменателе) Из этого соотношения и вытекает эффективный способ рекуррентного вычисления значений биномиальных коэффициентов. Докажем соотношение 1) Это может использоваться при вычислениях, например, вместо можно вычислить . Докажем соотношение 2) Имеется формула, называемая биномом Ньютона, которая использует выражения числа сочетаний с повторениями где а, b – действительные или комплексные числа. Коэффициенты называются биномиальными. Докажем формулу бинома Ньютона по индукции. Доказательство по индукции предполагает: 1) базис индукции – доказательство того, что формула верна для конкретного n , например, для n =1. В нашем случае мы убедились, что формула верна для n =2,3,4. Убедимся, что она верна и для n =1. 2) индукционный шаг. Предполагая, что формула верна для некоторого n , убеждаются, что тогда она верна и для n +1. 3) при истинности шагов 1 и 2 заключают, что формула верна для любого n . Приступим к индукционному шагу. Возьмем выражение и получим из него выражение для n +1. Очевидно, что это можно сделать путем умножения на a + b : Преобразуем полученное выражение: Для выполнения индукционного шага необходимо показать, что это выражение равно выражению: Рассмотрим подвыражение выражения (1): и заменим i на i -1. Получим , т.е. одинаковые коэффициенты перед выражениями , для числа сочетаний в первом и втором подвыражении выражения (1).Это позволит вынести за скобку. Но тогда в не учтен n -й член подвыражения (суммирование идет до n ): тогда, учитывая его, получаем: Нетрудно видеть, что можно заменить на , кроме того, мы уже доказали, что , поэтому: , что, очевидно, равно выражению: По индукции получаем, что формула бинома Ньютона верна для любого n . С использованием бинома Ньютона докажем следствие №1 о количестве подмножеств множества из n элементов: Рассмотрим следствие №2: . На использовании бинома Ньютона основано понятие производящей функции – функции, позволяющей получать комбинаторные числа без вычисления факториала: . Здесь – функция, производящая биномиальные коэффициенты. При n =1 получаем 1+ x , т.е. (коэффициент перед 1), (коэффициент перед x ). При n =2 получаем (1+ x ) 2 =1+2 x + x 2 , т.е. и т.д. Решение комбинаторных уравнений В комбинаторике тоже могут решаться уравнения, особенностью которых является то, что неизвестная принадлежит множеству натуральных чисел. Например, уравнения вида , xN , где N – множество натуральных чисел или вида: При решении комбинаторных уравнений часто необходимо уметь выполнять действия с факториалами типа: Например, в задаче о сравнении пар записей в базе данных из n записей: , – что и требовалось доказать. В комбинаторике рассматриваются и другие типовые комбинаторные комбинации, например, разбиения n -элементного множества на k подмножеств, которые называются блоками разбиения. В информатике вычисления на конечных математических структурах часто называют комбинаторными вычислениями, и они требуют комбинаторного анализа для установления свойств и оценки применимости используемых алгоритмов. На рис. 11 приведен один из возможных вариантов классификации основных комбинаций. Рис. 11. Основные комбинации Комбинаторные задачи могут быть решены, например, системой компьютерной математики Matematica (3,4) фирмы Wolfram Research , Inc . – пакет расширения «Дискретная математика» ( DiscreteMath ) – комбинаторика и ее функции ( Combinatorica , CombinatorialFunctions ): функции перестановок и сочетаний и др. Пример 1. Решить уравнение и представим правую часть в виде x + 3 = 11 и x = 8. Пример 2. Решить уравнение Решение. По условию x – целое число, удовлетворяющее неравенством откуда, после упрощений, получаем Пример 3. Решить систему уравнений Решение. Из второго уравнение находим Подставляя x = 18 в первое уравнение системы, найдем 18 – y = y + 2, y = 8. Итак, x = 18, y = 8. Пример 4. Решить систему уравнений Решение. Перепишем систему уравнений в виде
Решите уравнение (22–25) . 1) ОДЗ: х
ОДЗ: х
( 3) ОДЗ: х
4) 5 ОДЗ:
(20(х-2)-(х+1)(х+2)) (20х-40-х 2 +2х+х+2)=0 или х=0 или х-1=0 х 2 +3х-20х+42=0 х 1 =0 х 2 =1 х 2 -17х+42=0 корни 0 и 1 не входят в ОДЗ
х 1 =10 х 2 = — 3 (не входит в ОДЗ) 2)
4х(х-2)(х-1) = 6 х(4х 2 – 12х+8-30х+90)=0 х=0 или 4х 2 – 42х + 98 = 0 2х 2 – 21х + 49 = 0 4(х-2)! = 24 х 1 =12; х 2 = — 7(не входит в ОДЗ) х 1 =10; х 2 = 3 (не входит в ОДЗ) х 2 – 11х – 60 = 0 х 1 =15; х 2 = — 4(не входит в ОДЗ) 2 24х + х 2 + 7х + 12 – 324 = 0 х 2 + 31х – 312 = 0 х 1 =8; х 2 = — 39(не входит в ОДЗ) ОДЗ: (х-2)(х-1)х = 0 или (х-3)-45 = 0 х 1 =2; х 2 = 1 х 3 =0 — не входят в ОДЗ х 4 = 48 х 1 =10; х 2 = — 9(не входит в ОДЗ) x 2 +3 x +2–132 = 0 х 1 =10; х 2 = — 13(не входит в ОДЗ) x 2 +3 x +2– 110 = 0 x 2 +3 x – 108 = 0 х 1 =9; х 2 = — 12(не входит в ОДЗ) (х-3)(х-2)(х-1) = 3 4) Сколько двузначных чисел можно составить из цифр 1. 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр? Из 6 открыток надо выбрать 3. Сколькими способами это можно сделать? Комбинаторика основные понятия и формулы с примерами Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни. Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека. Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья. Представители того научного мира пытались найти методы решения таких задач, их базовые правила и понятия, утвердить уникальные формулы и уравнения для тех, кто ещё не встречался с ними. Такая информация в наше время называется информацией «для чайников». Попытаемся разобраться в аспектах этой области науки: каковы элементы, свойства, правила, методы и основное ее применение в нашей жизни? Конечно, всю область в одной статье невозможно охватить. Поэтому ниже будет представлено всё самое основное. Что такое комбинаторика в математикеСуть этого термина дают книги прошлых лет: это раздел математики, занимающийся операциями со множеством элементов. В интернете есть учебники по информатике и математике для детей, школьников, сборники материалов и задач для начинающих, где в доступном виде объяснена «занимательная» комбинаторика. Нужно твердо выяснить, как решать подобные задачи. В младших классах задачи на эту тему решают на дополнительных кружках, а в школах с углубленным изучением математики на основных уроках. К тому же, задачи по комбинаторике включены в олимпиады всех уровней. Основные понятия
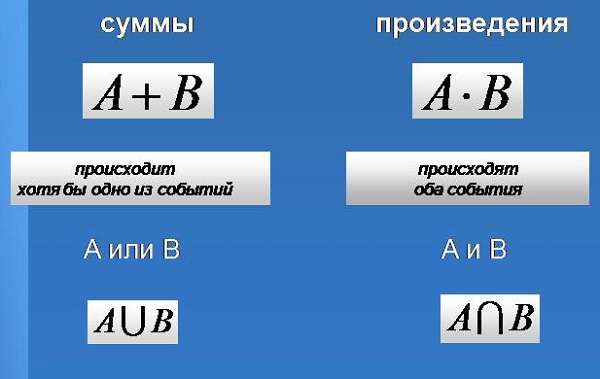
Правило произведенияЯвляется одним из основных правил при решении таких задач и звучит так: При выборе элемента А из n способов и выборе элемента В из m способов верно утверждение, что выбрать пару А и В одновременно можно n*m способами. Рассмотрим на конкретных примерах. Задача №1. В коробке лежит 2 мяча и 6 скакалок. Сколько существует способов достать 1 мяч и 1 скакалку? Ответ прост: 2 * 6 = 12. Задача №2. Есть 1 кубик, 2 шарика, 3 цветка и 4 конфеты. Сколькими способами можно вытянуть кубик, шарик, цветок и конфету? Решение аналогично: 1 * 2 * 3 * 4 = 24. Причем левую часть можно записать гораздо проще: 4! ! в данном случае является не знаком препинания, а факториалом. С помощью него можно вычислить более сложные варианты и решать трудные задачи (существуют разные формулы, но об этом позже). Задача №3. Сколько двузначных чисел можно составить из 2 цифр? Задача №4. Сколько десятизначных чисел можно составить из 10 цифр? Правило суммыТоже является базовым правилом комбинаторики. Если А можно выбрать n раз, а В — m раз, то А или В можно выбрать (n + m) раз. Задача №5. В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш? Ответ: 5 + 3 + 7 + 9 = 24. Сочетания с повторениями и без повторенийПод этим термином понимают комбинации в произвольном порядке из множества n по m элементов. Число сочетаний равно количеству таких комбинаций. Задача №6. В коробке находится 4 разных фрукта. Сколькими способами можно достать одновременно 2 разных фрукта? Где 4! – комбинация из 4 элементов. С повторениями чуть сложней, комбинации считаются по такой формуле: Задача №7. Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку. Размещения с повторениями и без повторений Под этим определением понимают набор m элементов из множества n элементов. Задача №8. Из 3 цифр надо выбрать 2, чтобы получались разные двузначные числа. Сколько вариантов? А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз! В таком случае общая формула будет выглядеть следующим образом: Задача №9. Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона. Перестановки с повторениями и без повторений Под этим термином понимают все возможные комбинации из n элементного множества. Задача №10. Сколько возможных пятизначных чисел можно составить из 5цифр? А шестизначных из 6 цифр? Семизначных из 7 цифр? Решения, согласно вышеприведенной формуле, следующие: А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше! Задача №11. В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать? Ответ прост: 4! / (3! * 1!) = 4. Комбинаторные задачи с решениямиПримеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.
ЗаключениеСтоит изучать эту науку, поскольку в век быстрой модернизации технологий потребуются специалисты, способные предоставить различные решения тех или иных практических задач. источники: http://urokimatematiki.ru/konspekt-uroka-na-temu-reshenie-kombinatornih-uravneniy-klass-5297.html http://tvercult.ru/nauka/kombinatorika-osnovnyie-ponyatiya-i-formulyi-s-primerami |

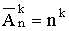
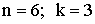
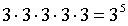 способов распределения по классам.
способов распределения по классам.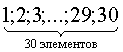 .
.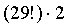 , т.к. комбинацию из 1 и 2 тома можно считать за один том, но при этом они могут стоять как (1;2) или (2;1), т.е.
, т.к. комбинацию из 1 и 2 тома можно считать за один том, но при этом они могут стоять как (1;2) или (2;1), т.е.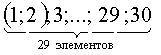 ,
, 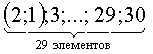 .
.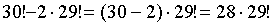
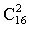 . Так как команды должны играть дважды число вариантов удваивается, т.е.
. Так как команды должны играть дважды число вариантов удваивается, т.е. 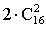 .
.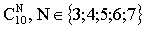 . Поэтому общее число вариантов есть
. Поэтому общее число вариантов есть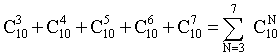 .
.
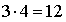 .
.
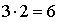 . Тогда всего вариантов маршрута
. Тогда всего вариантов маршрута 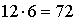 .
.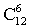 способами.
способами.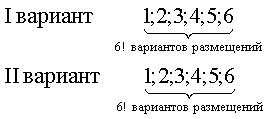
 .
.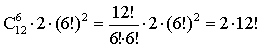 .
.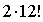 .
.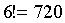 .
.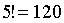 .
. 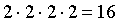 . Приведем другой наглядный способ решения, использующий так называемое “дерево решений”,который представляет все варианты (16 штук) получения экзаменационных оценок.
. Приведем другой наглядный способ решения, использующий так называемое “дерево решений”,который представляет все варианты (16 штук) получения экзаменационных оценок.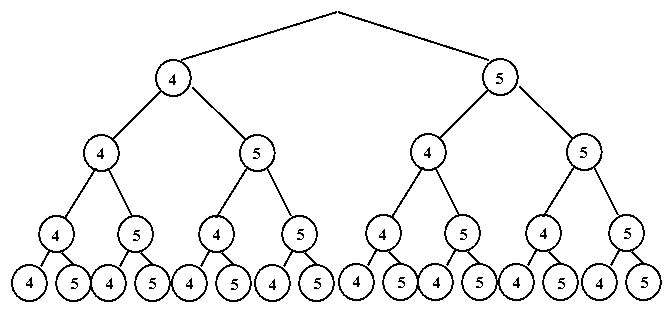 .
.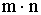 способами.
способами.
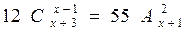
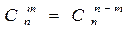
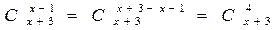 ,
,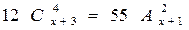
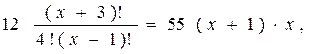
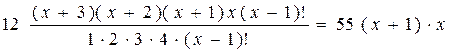 откуда следует
откуда следует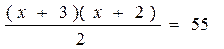
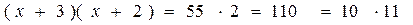
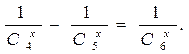
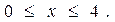 Перепишем уравнение в виде
Перепишем уравнение в виде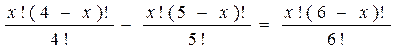
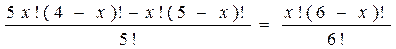
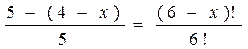
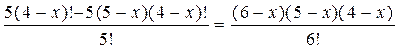
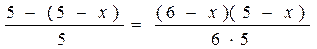
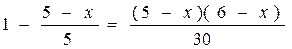
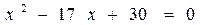
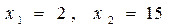 > 4
> 4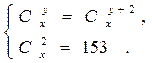
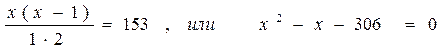 Решая последнее уравнение, получаем
Решая последнее уравнение, получаем 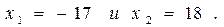 Но так как
Но так как 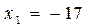 не пригодно к решению уравнения, значит x = 18.
не пригодно к решению уравнения, значит x = 18.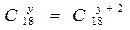
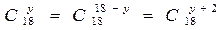
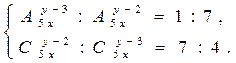
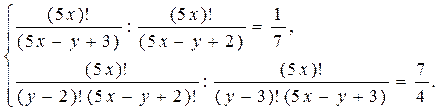 или, после упрощений получим
или, после упрощений получим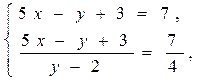 откуда следует x = 2, y = 6.
откуда следует x = 2, y = 6.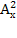 =42;
=42;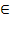 N; x > 2
N; x > 2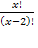 = 42
= 42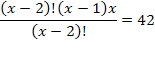
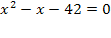
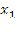 =-6( исключить – не входит в ОДЗ);
=-6( исключить – не входит в ОДЗ); 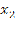 =7
=7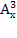 =56х;
=56х; N; x > 3
N; x > 3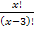 =
= 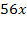
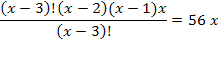
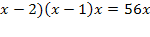
 ((
((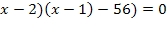
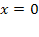 или
или 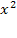 -3
-3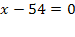
 1 =0(исключить) или х 2 =-6 (исключить); х 3 =9 (входит в ОДЗ).
1 =0(исключить) или х 2 =-6 (исключить); х 3 =9 (входит в ОДЗ).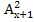 =30;
=30; N; x+1 > 2; х > 1
N; x+1 > 2; х > 1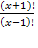 =
= 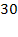
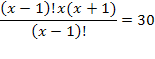
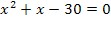
 =-6( исключить – не входит в ОДЗ);
=-6( исключить – не входит в ОДЗ);  =5.
=5.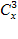 =
=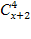 ;
;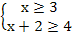
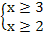 х
х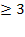
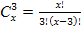 ;
; 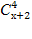 =
=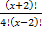
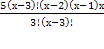 =
= 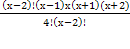
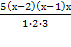 =
= 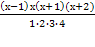
 х
х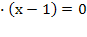
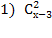 = 21 ОДЗ: х
= 21 ОДЗ: х N; x-3 > 2 ; x > 3
N; x-3 > 2 ; x > 3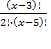 =
= 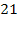
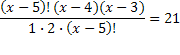
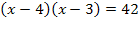
 — 7х + 12 – 42 = 0
— 7х + 12 – 42 = 0 — 7х – 30 = 0
— 7х – 30 = 0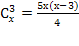 ; ОДЗ: х
; ОДЗ: х N; x > 3
N; x > 3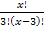 =
= 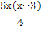
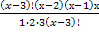 =
= 
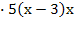
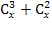 = 15(х-1) ОДЗ: х
= 15(х-1) ОДЗ: х N; x > 3
N; x > 3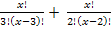 = 15(х-1)
= 15(х-1)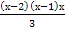 = (х-1)х х 1 = 0 или х 2 = 1 — не входят в ОДЗ
= (х-1)х х 1 = 0 или х 2 = 1 — не входят в ОДЗ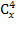 =
= 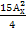 ОДЗ: х
ОДЗ: х N; x > 4
N; x > 4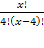 =
= 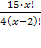
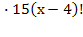
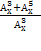 = 43 ОДЗ: х
= 43 ОДЗ: х N; x > 5
N; x > 5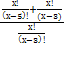 = 43
= 43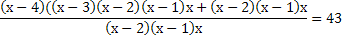
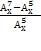 = 89 ОДЗ: х
= 89 ОДЗ: х N; x > 7
N; x > 7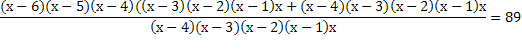
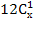 +
+ 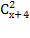 = 162 ОДЗ: х
= 162 ОДЗ: х N; x > 1
N; x > 1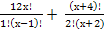 = 162
= 162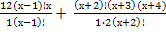 = 162
= 162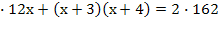
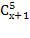 =
= 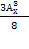
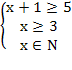 x > 4
x > 4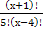 =
= 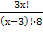
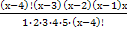 =
= 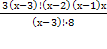
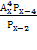 = 42 ОДЗ: х
= 42 ОДЗ: х N; x > 4
N; x > 4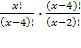 = 12
= 12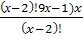 = 12 х 2 – х – 12 = 0 х 1 =4; х 2 = — 3(не входит в ОДЗ) Ответ: 4.
= 12 х 2 – х – 12 = 0 х 1 =4; х 2 = — 3(не входит в ОДЗ) Ответ: 4.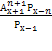 = 90 ОДЗ:
= 90 ОДЗ: 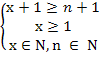
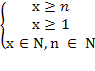
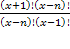 = 90
= 90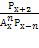 = 132 ОДЗ:
= 132 ОДЗ: 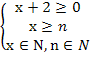
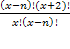 = 132
= 132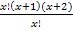 = 132
= 132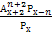 = 110 ОДЗ:
= 110 ОДЗ: 
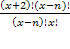 = 110
= 110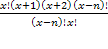 = 110
= 110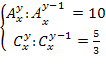 ОДЗ:
ОДЗ: 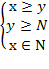
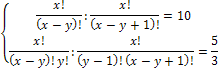
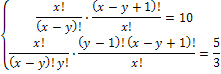
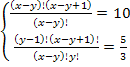
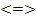
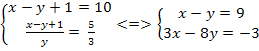
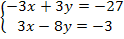 решаем методом сложения — 5у = -30; у = 6
решаем методом сложения — 5у = -30; у = 6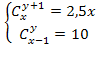 ОДЗ:
ОДЗ: 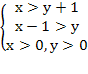
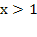 ; у
; у