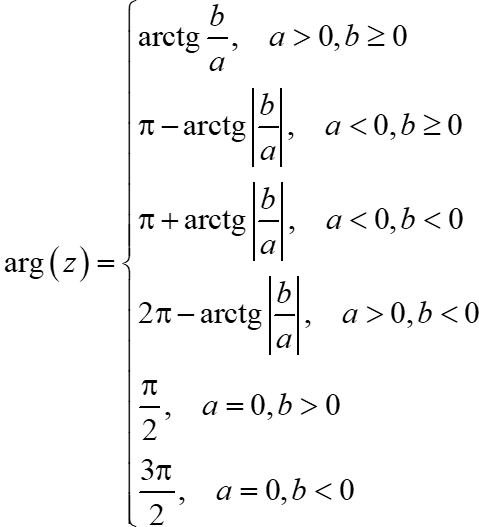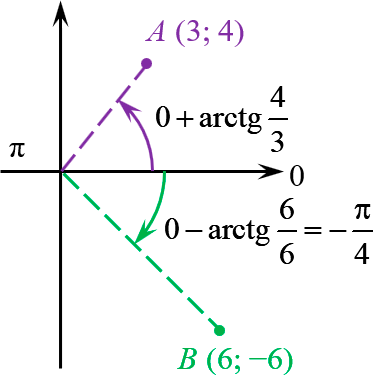Уравнения комплексные числа тригонометрическая форма

Тригонометрическая форма комплексного числа

Рассмотрим комплексное число, заданной в обычной (алгебраической) форме:

Задача заключается в представлении комплексного числа (1) в тригонометрической форме. Для этого на комплексной плоскости введем полярные координаты. Примем за полюс начало координат, а за полярную ось вещественную ось R.

Как известно, полярными координатами точки z являются длина r ее радиус-вектора, равной расстоянию от точки z до полюса, и величина ее полярного угла, т.е. угла, образованного между полярной осью и вектором-радиусом точки z. Отметим, что направление отсчета угла берется от полярной оси до вектора-радиуса против часовой стрелки (Рис.1, Рис.2).

На Рис.3 изображено комплексное число z. Координаты этого числа в декартовой системе координат (a, b). Из определения функций sin и cos любого угла, следует:

.

.

(2)

Подставляя (2) в (1), получим:

.

(3)

Эта форма записи называется тригонометрической формой записи комплексного числа.

Уравнения (2) возведем в квадрат и сложим:

.

(4)

r−длина радиус-вектора комплексного числа z называется модулем комплексного числа и обозначается |z|. Очевидно |z|≥0, причем |z|=0 тогда и только тогда, когда z=0.

Величина полярного угла точки, соответвующей комплексному числу z, т.е. угла φ, называется аргументом этого числа и обозначается arg z. Заметим, что arg z имеет смысл лишь при z≠0. Аргумент комплексного числа 0 не имеет смысла.

Аргумент комплексного числа определен неоднозначно. Если φ аргумент комплексного числа, то φ+2πk, k=0,1. также является аргументом комплексного числа, т.к. cos(φ+2πk)=cosφ, sin(φ+2πk)=sinφ.

Приведение комплексного числа из алгебраической формы в тригонометрическую

Пусть комплексное число представлено в алгебраической форме: z=a+bi. Представим это число в тригонометрической форме. Вычисляем модуль комплексного числа: . Вычисляем аргумент φ комплексного числа из выражений или . Полученные значения вставляем в уравнение (3).

Пример 1. Представить комплексное число z=1 в тригонометрической форме.

Решение. Комплексное число z=1 можно представить так: z=1+0i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=1/1. Откуда имеем φ=0. Подставляя значения модуля и аргумента в (3), получим: z=1(cos0+isin0).

Пример 2. Представить комплексное число z=i в тригонометрической форме.

Решение. Комплексное число z=i можно представить так: z=0+1i. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=0/1. Откуда имеем φ=π/2. Подставляя значения модуля и аргумента в (3), получим: .

Ответ. .

Пример 3. Представить комплексное число z=4+3i в тригонометрической форме.

Решение. Вычислим модуль этого числа: . Вычислим аргумент этого числа: cosφ=4/5. Откуда имеем φ=arccos(4/5). Подставляя значения модуля и аргумента в (3), получим: .

Ответ. , где φ=arccos(4/5).

Умножение комплексных чисел в тригонометрической форме записи

В результате умножения комплексных чисел в тригонометрической форме мы получили комплексное число в тригонометрической форме, следовательно |z₁z₂|=r₁r₂, или

т.е. модуль произведения комплексных чисел равен произведению модулей сомножителей .

т.е. аргумент произведения комплексных чисел равен сумме аргументов сомножителей .

Пример 4. Умножить комплексные числа и .

Решение. Воспользуемся формулой (5):

Ответ. .

Деление комплексных чисел в тригонометрической форме записи

(8)

Отсюда следует, что или

(9)

Далее , или

(10)

Следовательно, модуль частного двух комплексных чисел равен модулю делимого, деленному на модуль делителя, а аргумент частного двух комплексных чисел получается вычитанием аргумента делителя от аргумента делимого .

Пример 5. Делить комплексные числа и .

Решение. Воспользуемся формулой (8):

Ответ. .

Тригонометрическая форма комплексных чисел

Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».

Сегодня мы узнаем:

Начнём с ключевого определения.

1. Тригонометрическая форма

Определение. Тригонометрическая форма комплексного числа — это выражение вида

\[z=\left| z \right|\cdot \left( \cos \text< >\!\!\varphi\!\!\text< >+i\sin \text< >\!\!\varphi\!\!\text < >\right)\]

где $\left| z \right|$ — модуль комплексного числа, $\text< >\!\!\varphi\!\!\text< >$ — некоторый угол, который называется аргумент комплексного числа (пишут $\text< >\!\!\varphi\!\!\text< >=\arg \left( z \right)$).

Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:

Записать в тригонометрической форме число $z=\sqrt<3>+i$.

Переписываем исходное число в виде $z=\sqrt<3>+1\cdot i$ и считаем модуль:

Выносим модуль за скобки:

\[z=\sqrt<3>+1\cdot i=2\cdot \left( \frac<\sqrt<3>><2>+\frac<1><2>\cdot i \right)\]

Вспоминаем тригонометрию, 10-й класс:

Понятно, что вместо $\frac<\text< >\!\!\pi\!\!\text< >><6>$ с тем же успехом можно взять аргумент $\frac<13\text< >\!\!\pi\!\!\text< >><6>$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:

Записать в тригонометрической форме число $z=-1-i$.

2. Умножение и деление комплексных чисел

Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.

Теорема. Пусть даны два комплексных числа:

\[\begin & <_<1>>=\left| <_<1>> \right|\cdot \left( \cos \alpha +i\sin \alpha \right) \\ & <_<2>>=\left| <_<2>> \right|\cdot \left( \cos \beta +i\sin \beta \right) \\ \end\]

Тогда их произведение равно

\[<_<1>>\cdot <_<2>>=\left| <_<1>> \right|\cdot \left| <_<2>> \right|\cdot \left( \cos \left( \alpha +\beta \right)+i\sin \left( \alpha +\beta \right) \right)\]

А если ещё и $\left| <_<2>> \right|\ne 0$, то их частное равно

Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!

Найти произведение и частное двух комплексных чисел:

\[\begin <_<1>>\cdot <_<2>> & =2\cdot 5\cdot \left( \cos \left( \frac<\pi ><3>+\frac<\pi > <6>\right)+i\sin \left( \frac<\pi ><3>+\frac<\pi > <6>\right) \right)= \\ & =10\cdot \left( \cos \frac<\pi ><2>+i\sin \frac<\pi > <2>\right) \\ \end\]

\[\begin \frac<<_<1>>><<_<2>>> & =\frac<2><5>\cdot \left( \cos \left( \frac<\pi ><3>-\frac<\pi > <6>\right)+i\sin \left( \frac<\pi ><3>-\frac<\pi > <6>\right) \right)= \\ & =0,4\cdot \left( \cos \frac<\pi ><6>+i\sin \frac<\pi > <6>\right) \\ \end\]

По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)

3. Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

\[z=\left| z \right|\cdot \left( \cos \text< >\!\!\varphi\!\!\text< >+i\sin \text< >\!\!\varphi\!\!\text < >\right)\]

Возведём его в квадрат, умножив на само себя:

\[\begin <^<2>> & =z\cdot z = \\ & =\left| z \right|\left| z \right|\cdot \left( \cos \left( \text< >\!\!\varphi\!\!\text< + >\!\!\varphi\!\!\text < >\right)+i\sin \left( \text< >\!\!\varphi\!\!\text< + >\!\!\varphi\!\!\text < >\right) \right)= \\ & =<<\left| z \right|>^<2>>\cdot \left( \cos 2\text< >\!\!\varphi\!\!\text< >+i\sin 2\text< >\!\!\varphi\!\!\text < >\right) \\ \end\]

Затем возведём в куб, умножив на себя ещё раз:

Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.

Формула Муавра. При возведении всякого комплексного числа

\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]

в степень $n\in \mathbb$ получим

Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $n\in \mathbb$, а не только натуральном. Но об этом позже. Сейчас примеры:

Представим первое число в тригонометрической форме:

\[\begin \sqrt<3>-i & = 2\cdot \left( \frac<\sqrt<3>><2>+i\cdot \left( -\frac<1> <2>\right) \right)= \\ & =2\cdot \left( \cos \left( -\frac<\pi > <6>\right)+i\sin \left( -\frac<\pi > <6>\right) \right) \\ \end\]

По формуле Муавра:

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Теперь второе число запишем в комплексной форме:

По формуле Муавра:

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

4. Дополнение 1. Геометрический подход

Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:

А есть полярная система координат, где точки задаются поворотом на угол $\varphi $ и расстоянием до центра $r$:

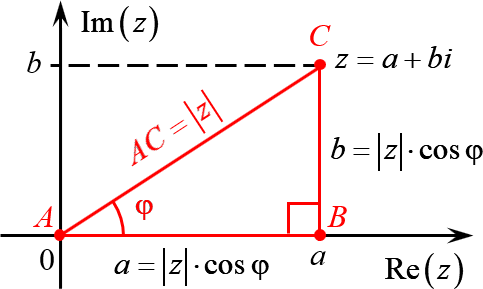
А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:

Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние

Треугольник $ABC$ — прямоугольный. Пусть $\angle BAC=\varphi $. Тогда:

\[\begin & AB=AC\cdot \cos \varphi =\left| z \right|\cdot \cos \varphi \\ & BC=AC\cdot \sin \varphi =\left| z \right|\cdot \sin \varphi \\ \end\]

С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:

\[\begin a+bi & =\left| z \right|\cos \varphi +i\cdot \left| z \right|\sin \varphi = \\ & =\left| z \right|\left( \cos \varphi +i\sin \varphi \right) \\ \end\]

Итак, мы перешли от пары $\left( a;b \right)$ к паре $\left( \left| z \right|;\varphi \right)$, где $\left| z \right|$ — модуль комплексного числа, $\varphi $ — его аргумент (проще говоря, угол поворота).

Важное замечание. А кто сказал, что такой угол $\varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:

Осталось подобрать такой угол $\varphi $, чтобы выполнялось два равенства:

Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:

На практике основная трудность заключается именно в поиске подходящего аргумента.

5. Дополнение 2. Как найти аргумент?

В учебниках пишут много разной дичи, типа вот этой:

Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.

5.1. Точки на координатных осях

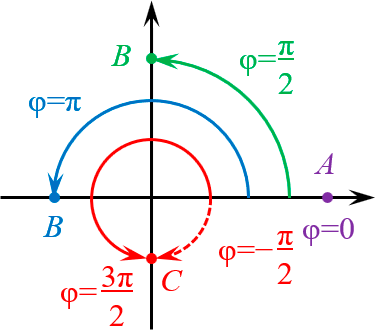
Для начала рассмотрим точки, лежащие осях координат.

Тут всё очевидно:

• На положительной полуоси абсцисс $\varphi =0$ (фиолетовая точка $A$).
• На отрицательной — $\varphi =\pi $ (синяя точка $B$).
• На положительной полуоси ординат $\varphi =\frac<\pi ><2>$ (зелёная точка $B$).
• На отрицательной — $\varphi =\frac<3\pi ><2>$ (красная точка $C$). Однако ничто не мешает рассмотреть $\varphi =-\frac<\pi ><2>$ — результат будет тем же самым.:)

5.2. Точки с арктангенсом

А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $a\ne 0$ и $b\ne 0$. Рассмотрим вспомогательный угол

Очевидно, это острый угол:

Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол $<<\varphi >_<1>>$ от горизонтальной оси в эту четверть.

В правой полуплоскости мы откладываем от «нулевого» луча:

Точка $A\left( 3;4 \right)$ удалена от начала координат на расстояние 5:

\[\begin 3+4i & =5\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\operatorname\frac<4> <3>\end\]

Для точки $B\left( 6;-6 \right)$ арктангенс оказался табличным:

\[6-6i=6\sqrt<2>\cdot \left( \cos \left( -\frac<\pi > <4>\right)+i\sin \left( -\frac<\pi > <4>\right) \right)\]

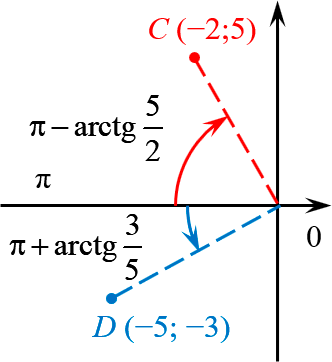
В левой полуплоскости откладываем от луча, соответствующего углу $\pi $:

Итого для точки $C\left( -2;5 \right)$ имеем:

\[\begin -2+5i & =\sqrt<29>\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\pi -\operatorname\frac<5> <2>\end\]

И, наконец, для точки $D\left( -5;-3 \right)$:

\[\begin -5-3i & =\sqrt<34>\cdot \left( \cos \varphi +i\sin \varphi \right) \\ \varphi & =\pi +\operatorname\frac<3> <5>\end\]

Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.

А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)

Формы записи комплексного числа: тригонометрическая, показательная

В данной публикации рассмотрена тригонометрическая форма комплексного числа с интерпретацией на коордлинатной плоскости, формулами расчета аргумента и примером для лучшего понимания изложенного материала. Также представлена базовая информация по показательной форме данного типа числа.

Тригонометрическая форма комплексного числа

Любое комплексное число (за искл. нуля) вида можно записать в тригонометрической форме следующим образом:

z = |z| ⋅ (cos φ + i ⋅ sin φ)

Чтобы было понятнее, покажем комплексное число на координатной плоскости. При этом, в качестве примера будем исходить из того, что a и b больше нуля.

Модуль комплексного числа |z| – это расстояние от начала координат до соответствующей точки на комплексной плоскости, другими словами, это длина зеленого вектора на чертеже выше.

Исходя из теоремы Пифагора модуль вычисляется так:

Аргумент комплексного числа ( φ ) – угол между положительной полуосью действительной оси (RE) и вектором, который проведен из начала координат. Аргумент не существует для , может обозначаться как .

Формула для расчета аргумента зависит от того, какие значения принимают a и b .