Дифференциальные уравнения первого порядка, приводящиеся к линейным
Метод решения
К линейным уравнениям первого порядка приводится уравнения вида:
(1) ,
где z – функция от y ; p и q – функции от x .
Действительно, по правилу дифференцирования сложной функции:
.
Подставляя в (1), получаем уравнение, линейное относительно z :
.
Дифференциальные уравнения, линейные относительно переменной x
Ранее мы рассматривали уравнения, линейные относительно переменной y . То есть мы считали, что x является независимой переменной, а y является зависимой переменной. Однако, всегда стоит иметь в виду, что возможен противоположный подход. То есть можно считать переменную y независимой переменной, а x – зависимой переменной. На практике часто встречаются задачи, в которых уравнение линейно относительно переменной x , а не y . В общем виде такое уравнение можно записать так:
(2) ,
где P, Q, R –функции от y .
Покажем, что это уравнение линейно относительно переменной x . Для этого выполняем преобразования. Представим производную в виде отношения дифференциалов:
.
Тогда уравнение (2) примет вид:
.
Умножаем на и выполняем алгебраические преобразования:
;
.
Разделив на R ( y ) , приводим уравнение к виду:
,
где .
Это – линейное относительно x дифференциальное уравнение.
Пример решения дифференциального уравнения, приводящегося к линейному уравнению первого порядка
Решить уравнение:
(П.1) .
Подставим в (П.1):
.
Считаем, что y – это независимая переменная, а x – зависимая. То есть x – это функция от y . Умножим на :
(П.2) .
Делаем подстановку:
.
Здесь z – сложная функция от y , .
Дифференцируем по y . По правилу дифференцирования сложной функции:
.
Подставляем в (П.2):
;
.
Это линейное, относительно z , дифференциальное уравнение. Решаем его с помощью интегрирующего множителя. Умножаем уравнение на интегрирующий множитель e y :
;
;
.
Интегрируем по частям:
;
;
;
.
Переходим к переменной x :
;
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 05-08-2012 Изменено: 26-06-2015
Методика введения решения линейных уравнений и уравнений, сводящихся к линейным
Разделы: Математика
Изучение уравнений в среднем звене начинается с введения решения линейных уравнений и уравнений, сводящихся к линейным.
Равенство двух функций, рассматриваемых в общей области определения, называется уравнением. Переменные, входящие в уравнение, обозначаются латинскими буквами x, y,z, t … Уравнение с одной переменной х в общем, виде записывается так f(x)= g(x).
Всякое значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называется корнем уравнения.
Решить уравнение – это, значит, найти все его корни или доказать, что их нет.
Например, уравнение 3+x=7 имеет единственный корень 4, так как при этом и только при этом значении переменной 3+x=7 верное равенство.
Уравнение (x-1)(x-2)=0 имеет 2 корня 1 и 2.
Уравнение x 2 +1=0 не имеет действительных корней, так как сумма двух положительных чисел не равняется 0.
Для того, чтобы решить любое уравнение с одной переменной, учащийся должен знать: во-первых, правила, формулы или алгоритмы решения уравнений данного вида и, во-вторых, правила выполнения тождественных и равносильных преобразований, с помощью которых данное уравнение можно привести к простейшим.
Таким образом, решение каждого уравнения складывается из двух основных частей:
- преобразования данного уравнения к простейшим;
- решения простейших уравнений по известным правилам, формулам или алгоритмам.
Если вторая часть является алгоритмической, то первая часть — в значительной степени — эвристической, что и представляет наибольшую трудность для учащихся. В процессе решения уравнения его стараются заменить более простым, поэтому важно знать с помощью каких преобразований это возможно. Здесь необходимо в доступной для ребенка форме дать понятие равносильности.
Уравнения, имеющие одни и теже корни, называются равносильными. Равносильными считаются и уравнения, каждое из которых не имеет корней.
Например, уравнения x+2=5 и x+5=8 равносильны, так как каждое из них имеет единственный корень — число 3.Равносильны и уравнения x 2 +1=0 и 2x 2 +5=0 — ни одно из них не имеет корней.
Уравнения х-5=1 и х 2 =36 не равносильны, так как первое имеет только один корень х=6, тогда как второе имеет два корня 6 и –6.
К равносильным преобразованиям относятся:
1) Если к обеим частям уравнения прибавить одно и тоже число или одно и тоже целое алгебраическое выражение, содержащее неизвестное, то новое уравнение будет равносильно данному.
2) Если обе части уравнения умножить или разделить на одно и тоже отличное от нуля число, то получится уравнение, равносильное данному.
Например, уравнение 
3) Если в уравнении произвести раскрытие скобок и привести подобные слагаемые, то получится уравнения, равносильно данному.
Обучение решения уравнений начинается с простейших линейных уравнений и уравнений сводящихся к ним. Дается определение линейного уравнения и рассматриваются случаи, когда оно имеет одно решение; не имеет решений и имеет бесконечное множество решений.
Линейным уравнением с одной переменной х называют уравнение вида ах = b, где а и b — действительные числа, а — называют коэффициентом при переменной, b — свободным членом.
Для линейного уравнения ах = b могут представиться при случае:
- а
0, в этом случае корень уравнения равен b/a
- а = 0; b = 0; в этом случае уравнение принимает вид 0
х = b, что верно при любом х, т.е. корнем уравнения служит любое действительное число;
- а = 0; b
0; в том случае уравнение принимает вид 0
х = b, оно не имеет корней.
Многие уравнения в результате преобразований сводятся к линейным.
Так в 7 классе можно применить следующие уравнения:
1)
Это уравнение сводиться к линейному уравнению.
Умножением обеих частей на 12 (наименьшее общее краткое знаменателей 3, 4, 6, 12), получим:
8 + 3x + 2 – 2x = 5x –12,
8 + 2 + 12 = 5x – 3x + 2x,
2) Покажем, что уравнение 2 (х + 1) – 1 = 3 — (1 — 2х) не имеет корней.
Упростим обе части уравнения:
2х + 2 – 1 = 3 – 1 + 2х,
Это уравнение не имеет корней, т.к. левая часть 0 х равна 0 при любом х, а значит не равна 1.
3) Покажем, что уравнение 3(1 – x) + 2 = 5 – 3x имеет бесконечное множество корней.
При прохождении темы “линейные уравнения с двумя переменными” можно предложить учащимся графический способ решения уравнения. Данный метод основан на пользовании графиков функций, входящих в уравнение. Суть метода: найти абсциссы точек пересечения графиков функций, стоящих в левой и правой частях уравнения. Основывается на выполнение следующих действий:
1) Преобразовать исходное уравнение к виду f(x) = g(x), где f(x) и g(x) функции, графики, которых можно построить.
2) Построить графики функций f(x) и g(x)
3) Определить точки пересечения построенных графиков.
4) Определить абсциссы найденных точек. Они и дадут множество решений исходного уравнения.
5) Записать ответ.
Преимущество данного метода заключается в том, что он позволяет легко определить число корней уравнения. Недостаток в том, что корни в общем случае определяются приближенно.
Следующим этапом в изучении линейных уравнений, являются уравнения с модулями, причем некоторые решения выполняются несколькими способами.
Решение уравнений, содержащих знак модуля и уравнений с параметрами можно назвать деятельностью, близкой к исследовательской. Это обусловлено тем, что выбор метода решения, процесс решения, запись ответа предполагают определенный уровень сформированности умений наблюдать, сравнивать, анализировать, выдвигать и проверять гипотезу, обобщать полученные результаты.
Особой интерес представляют уравнения, содержащие знак модуля.
По определению модуля числа a, имеем:
Число –a может быть отрицательным при a>0; -a положительным при a -1, тогда

Видим, что число 0 принадлежит промежутку. Значит, является корнем. Таким образом, уравнение 
На простых примерах рассмотрим алгоритм решения уравнений с параметрами: область допустимых значений, область определения, общие решения, контрольные значения параметров, типы частных уравнений. Способы их нахождения будут устанавливаться в каждом виде уравнений отдельно.
На базе введенных понятий определим общую схему решения всякого уравнения F(a;x)=0 с параметром а (для случая двух параметров схема аналогична):
- устанавливаются область допустимых значений параметра и область определения;
- определяются контрольные значения параметра, разбивающие область допустимых значений параметра на области однотипности частных уравнений;
- для контрольных значений параметра соответствующие частные уравнения исследуются отдельно;
- находятся общие решения x=f1 (a),…, fk (a) уравнения F(a;x)=0 на соответствующих множествах Аf1,…, Аfk значений параметра;
- составляется модель общих решений, контрольных значений параметра;
- на модели выделяются промежутки значений параметра с одинаковыми общими решениями (области однотипности);
- для контрольных значений параметра и выделенных областей однотипности записываются характеристики всех типов частных уравнений
- Особое место в алгебре отводится линейным уравнениям с параметрами.
Рассмотрим несколько примеров.
| 1. | 2х – 3 = m +1, +1, |
2х – 3 = 
Умножим обе части уравнения на 3, получим
6х — m•х + 12m + 12,

 , при m
, при m  6.
6.Уравнение 2х – 3 + m (х/3 + 4) + 1 имеет множество решений, заданных формулой 
2. 



mx – n = 2x – 2 + 2n + 3xn,
mx – 2x – 3xn = — 2 + 2n +n,
mx – 2x – 3xn = 3n – 2,
x (m – 2 – 3n) = 3n – 2, при m 


Рассмотрим случай, где a = 0, тогда
m = 3n +2, при n 
n = 
m = 3 • 
x(4 – 2 – 3 

x – любое число, кроме x = 1.
б) 3n – 2 
0 • x = b. В этом случае уравнение не имеет решений.
2) a 
m – 2 – 3n 
m 
x = 


3n – 2 
3n + 3n 
6n 

В этом случае уравнение решений не имеет.
Значит, при n = 
(n 


Ответ: 1. n = 

2. n = 0, m = 6n (n 

3. n 




В дальнейшем предлагается рассмотреть решение задач методом составления линейных уравнений. Это сложный процесс, где надо уметь думать, догадываться, хорошо знать фактически материал.
В процессе решения каждой задачи надо четко размечать четыре этапа:
- изучение условия задачи;
- поиск плана решения и его составление;
- оформление найденного решения;
- критический анализ результата решения.
Теперь рассмотрим задачи, при решении которых применяются линейные уравнения.
1. Сплав меди и цинка содержит меди на 640 г. Больше, чем цинка. После того, как из сплава выделили 6/7 содержащейся в нем меди и 60% цинка, масса сплава оказалась равной 200 г. Какова была масса сплава первоначально?
Пусть в сплаве было х г. цинка, тогда меди (640 + х) г. после того, как выделили 6/7 меди и 60% цинка, осталось 1/7 меди и 40% цинка, т.е. 0,4 части. Зная, что масса сплава оказалась равной 200 г., составим уравнение.
1/7 (х + 640) + 0,4•х = 200,
х + 640 + 2,8•х =1400,
Значит, цинка было 200 г., а меди 840 г.
(200 + 640 = 840). 1) 200 + 840 = 1040 (г.) – масса сплава. Ответ: первоначальная масса сплава 1040 г.
2. Сколько литров 60% серной кислоты нужно прибавить к 10 л 30% кислоты, чтобы получить 40% раствор?
Пусть число литров 60% кислоты, которое прибавим х л, тогда раствора чистой кислоты будет 





60х + 300 = 40х + 400,
60х – 40х = 400 – 300,
Значит, нужно прибавить 5 л 60% кислоты.
При изучении темы “Решение линейных уравнений” рекомендуется некоторая историческая справка.
Задачи на решение уравнений первой степени встречаются еще в вавилонских клинописных текстах. В них же есть некоторые задачи, приводящие к квадратным и даже кубическим уравнениям (последние, по-видимому, решались с помощью подбора корней). Древнегреческие математики нашли геометрическую форму решения квадратного уравнения. В геометрической же форме арабский математик Омар Хайям (конец XI – начало XII века н. э.) исследовал кубическое уравнение, хотя и не нашел общей формулы для его решения. Решение кубического уравнения было найдено в начале XVI века в Италии. После того, как Сципиан дель Ферро решил один частный вид таких уравнений в 1535 году, итальянец Тарталья нашел общую формулу. Он доказал, что корни уравнения x 3 + px + q = 0 имеют вид x =
Это выражение обычно называют формулой Кардано, по имени ученого, узнавшего ее от Тартальи и опубликовавшего в 1545 году в своей книге “Великое искусство алгебраических правил”. Ученик Кардано – молодой математик Феррари решил общее уравнение четвертой степени. После этого на протяжении двух с половиной столетий продолжались поиски формулы для решения уравнений пятой степени. В 1823 году замечательный норвежский математик Нильс Хендрик Абель (1802-1829) доказал, что такой формулы не существует. Точнее говоря, он доказал, что корни общего уравнения пятой степени нельзя выразить через его коэффициенты с помощью арифметических действий и операций извлечения корня. Глубокое исследование вопроса об условиях разрешимости уравнений в радикалах провел французский математик Эварист Галуа (1811-1832), погибший на дуэли в возрасте 21 года. Некоторые проблемы теории Галуа решил советский алгебраист И.Т.Шафаревич.
Наряду с поисками формулы для решения уравнения пятой степени велись и другие исследования в области теории алгебраических уравнений. Виета установил связь между коэффициентами уравнений и его корнями. Он доказал, что если x1,…,xn – корни уравнения x n + a1x n-1 +…+an=0, то имеют место формулы:
Литература:
- Журнал “Математика в школе” 6, 1999
- Приложение к газете “Первое сентября”- математика 20, 1999.
- С.И. Туманов “Алгебра”, пособие для учащихся 6-8 классов.
- Н.И. Александров; И. П.Ярандай “Словарь-справочник по математике”.
- О.Б. Епишева; В.И. Крупич “Учить школьников учиться математике”.
- Е.И.Ямщенко “Изучение функций”.
- А.И. Худобин; М.Ф. Шуршалов “Сборник задач по алгебре и элементарным функциям”.
- Ш. А. Алимов, В.А. Ильин “Алгебра 6-8 классы”.
Виды дифференциальных уравнений
Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.
В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.
Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.
Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.
Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».
Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1 -го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2 -го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.
Напомним, что y ‘ = d x d y , если y является функцией аргумента x .
Дифференциальные уравнения первого порядка
Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )
Начнем с примеров таких уравнений.
y ‘ = 0 , y ‘ = x + e x — 1 , y ‘ = 2 x x 2 — 7 3
Оптимальным для решения дифференциальных уравнений f ( x ) · y ‘ = g ( x ) является метод деления обеих частей на f ( x ) . Решение относительно производной позволяет нам прийти к уравнению вида y ‘ = g ( x ) f ( x ) . Оно является эквивалентом исходного уравнения при f ( x ) ≠ 0 .
Приведем примеры подобных дифференциальных уравнений:
e x · y ‘ = 2 x + 1 , ( x + 2 ) · y ‘ = 1
Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х , при которых функции f ( x ) и g ( x ) одновременно обращаются в 0 . В качестве дополнительного решения в уравнениях f ( x ) · y ‘ = g ( x ) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х .
Наличие дополнительных решений возможно для дифференциальных уравнений x · y ‘ = sin x , ( x 2 — x ) · y ‘ = ln ( 2 x 2 — 1 )
Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1 -го порядка».
Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )
Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f ( y ) d y = g ( x ) d x . Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у , разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.
Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x
К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:
y 2 3 d y = sin x d x , e y d y = ( x + sin 2 x ) d x
Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f 2 ( y ) ⋅ g 1 ( x ) . Так мы придем к уравнению f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x . Преобразование можно будет считать эквивалентным в том случае, если одновременно f 2 ( y ) ≠ 0 и g 1 ( x ) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.
В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: d y d x = y · ( x 2 + e x ) , ( y 2 + a r c cos y ) · sin x · y ‘ = cos x y .
К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = a x + b y . Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y ‘ = f ( a x + b y ) , a , b ∈ R .
Подставив z = 2 x + 3 y в уравнение y ‘ = 1 e 2 x + 3 y получаем d z d x = 3 + 2 e z e z .
Заменив z = x y или z = y x в выражениях y ‘ = f x y или y ‘ = f y x , мы переходим к уравнениям с разделяющимися переменными.
Если произвести замену z = y x в исходном уравнении y ‘ = y x · ln y x + 1 , получаем x · d z d x = z · ln z .
В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.
Предположим, что в условии задачи нам дано уравнение y ‘ = y 2 — x 2 2 x y . Нам необходимо привести его к виду y ‘ = f x y или y ‘ = f y x . Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x 2 или y 2 .
Нам дано уравнение y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R .
Для того, чтобы привести исходное уравнение к виду y ‘ = f x y или y ‘ = f y x , нам необходимо ввести новые переменные u = x — x 1 v = y — y 1 , где ( x 1 ; y 1 ) является решением системы уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0
Введение новых переменных u = x — 1 v = y — 2 в исходное уравнение y ‘ = 5 x — y — 3 3 x + 2 y — 7 позволяет нам получить уравнение вида d v d u = 5 u — v 3 u + 2 v .
Теперь выполним деление числителя и знаменателя правой части уравнения на u . Также примем, что z = u v . Получаем дифференциальное уравнение с разделяющимися переменными u · d z d u = 5 — 4 z — 2 z 2 3 + 2 z .
Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».
Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )
Приведем примеры таких уравнений.
К числу линейных неоднородных дифференциальных уравнений 1 -го порядка относятся:
y ‘ — 2 x y 1 + x 2 = 1 + x 2 ; y ‘ — x y = — ( 1 + x ) e — x
Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y ( x ) = u ( x ) v ( x ) . Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».
Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a
Приведем примеры подобных уравнений.
К числу дифференциальных уравнений Бернулли можно отнести:
y ‘ + x y = ( 1 + x ) e — x y 2 3 ; y ‘ + y x 2 + 1 = a r c t g x x 2 + 1 · y 2
Для решения уравнений этого вида можно применить метод подстановки z = y 1 — a , которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1 -го порядка. Также применим метод представления функции у в качестве y ( x ) = u ( x ) v ( x ) .
Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.
Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0
Если для любых значений x и y выполняется ∂ P ( x , y ) ∂ y = ∂ Q ( x , y ) ∂ x , то этого условия необходимо и достаточно, чтобы выражение P ( x , y ) d x + Q ( x , y ) d y представляло собой полный дифференциал некоторой функции U ( x , y ) = 0 , то есть, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y . Таким образом, задача сводится к восстановлению функции U ( x , y ) = 0 по ее полному дифференциалу.
Выражение, расположенное в левой части записи уравнения ( x 2 — y 2 ) d x — 2 x y d y = 0 представляет собой полный дифференциал функции x 3 3 — x y 2 + C = 0
Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».
Дифференциальные уравнения второго порядка
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R
Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k 2 + p k + q = 0 . Здесь возможны три варианта в зависимости от различных p и q :
- действительные и различающиеся корни характеристического уравнения k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
- действительные и совпадающие k 1 = k 2 = k , k ∈ R ;
- комплексно сопряженные k 1 = α + i · β , k 2 = α — i · β .
Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:
- y = C 1 e k 1 x + C 2 e k 2 x ;
- y = C 1 e k x + C 2 x e k x ;
- y = e a · x · ( C 1 cos β x + C 2 sin β x ) .
Пример 13
Предположим, что у нас есть линейное однородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами y ‘ ‘ + 3 y ‘ = 0 . Найдем корни характеристического уравнения k 2 + 3 k = 0 . Это действительные и различные k 1 = — 3 и k 2 = 0 . Это значит, что общее решение исходного уравнения будет иметь вид:
y = C 1 e k 1 x + C 2 e k 2 x ⇔ y = C 1 e — 3 x + C 2 e 0 x ⇔ y = C 1 e — 3 x + C 2
Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами».
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R
Основным способом решение уравнений данного вида является нахождение суммы общего решения y 0 , которое соответствует линейному однородному дифференциальному уравнению y ‘ ‘ + p y ‘ + q y = 0 , и частного решения y
исходного уравнения. Получаем: y = y 0 + y
Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y
мы можем методом неопределенных коэффициентов при определенном виде функции f ( x ) , которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.
К числу линейных неоднородных дифференциальных уравнений 2 -го порядка с постоянными коэффициентами относятся:
y ‘ ‘ — 2 y ‘ = ( x 2 + 1 ) e x ; y ‘ ‘ + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x
Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2 -го порядка с постоянными коэффициентами».
Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )
Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.
На некотором отрезке [ a ; b ] общее решение линейного однородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 представлено линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, y = C 1 y 1 + C 2 y 2 .
Частные решения мы можем выбрать из систем независимых функций:
1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 x , e k 2 x , . . . , e k n x 3 ) e k 1 x , x · e k 1 x , . . . , x n 1 · e k 1 x , e k 2 x , x · e k 2 x , . . . , x n 2 · e k 2 x , . . . e k p x , x · e k p x , . . . , x n p · e k p x 4 ) 1 , c h x , s h x
Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.
Возьмем для примера линейное однородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = 0 .
Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y
, где y 0 — общее решение соответствующего ЛОДУ, а y
частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y
нам поможет метод вариации произвольных постоянных.
Возьмем для примера линейное неоднородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = x 2 + 1 .
Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».
Дифференциальные уравнения высших порядков
Дифференциальные уравнения, допускающие понижение порядка
Мы можем провести замену y ( k ) = p ( x ) для того, чтобы понизить порядок исходного дифференциального уравнения F ( x , y ( k ) , y ( k + 1 ) , . . . , y ( n ) ) = 0 , которое не содержит искомой функции и ее производных до k — 1 порядка.
В этом случае y ( k + 1 ) = p ‘ ( x ) , y ( k + 2 ) = p ‘ ‘ ( x ) , . . . , y ( n ) = p ( n — k ) ( x ) , и исходное дифференциальное уравнение сведется к F 1 ( x , p , p ‘ , . . . , p ( n — k ) ) = 0 . После нахождения его решения p ( x ) останется вернуться к замене y ( k ) = p ( x ) и определить неизвестную функцию y .
Дифференциальное уравнение y ‘ ‘ ‘ x ln ( x ) = y ‘ ‘ после замены y ‘ ‘ = p ( x ) станет уравнением с разделяющимися переменными y ‘ ‘ = p ( x ) , и его порядок с третьего понизится до первого.
В уравнении, которое не содержит аргумента х и имеет вид F ( y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 , порядок может быть заменен на единицу следующим образом: необходимо провести замену d y d x = p ( y ) , где p ( y ( x ) ) будет сложной функцией. Применив правило дифференцирования, получаем:
d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.
Рассмотрим решение уравнения 4 y 3 y ‘ ‘ = y 4 — 1 . Путем замены d y d x = p ( y ) приведем исходное выражение к уравнению с разделяющимися переменными 4 y 3 p d p d y = y 4 — 1 .
Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )
Решение уравнений данного вида предполагает выполнение следующих простых шагов:
- находим корни характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 ;
- записываем общее решение ЛОДУ y 0 в стандартной форме, а общее решение ЛНДУ представляем суммой y = y 0 + y
— частное решение неоднородного дифференциального уравнения.
Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y
целесообразно использовать метод вариации произвольных постоянных.
Линейному неоднородному ДУ с постоянными коэффициентами y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = x cos x + sin x соответствует линейное однородное ДУ y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = 0 .
Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )
Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y
, где y 0 — общее решение соответствующего ЛОДУ, а y
— частное решение неоднородного дифференциального уравнения.
y 0 представляет собой линейную комбинацию линейно независимых функций y 1 , y 2 , . . . , y n , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 в тождество. Частные решения y 1 , y 2 , . . . , y n обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.
После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y
Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».
Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2
Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.
http://urok.1sept.ru/articles/410415
http://zaochnik.com/spravochnik/matematika/differentsialnye-uravnenija/vidy-differentsialnyh-uravnenij/
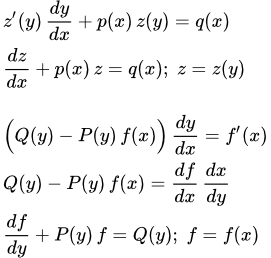
 0, в этом случае корень уравнения равен b/a
0, в этом случае корень уравнения равен b/a х = b, что верно при любом х, т.е. корнем уравнения служит любое действительное число;
х = b, что верно при любом х, т.е. корнем уравнения служит любое действительное число; 0; в том случае уравнение принимает вид 0
0; в том случае уравнение принимает вид 0 х = b, оно не имеет корней.
х = b, оно не имеет корней.

