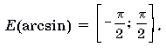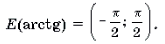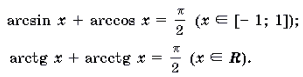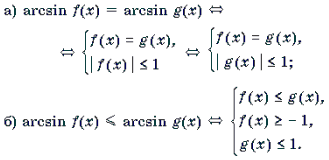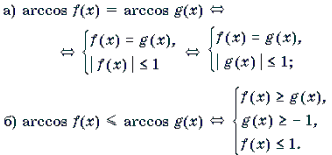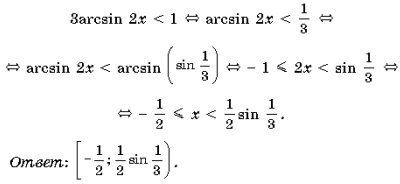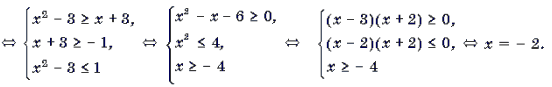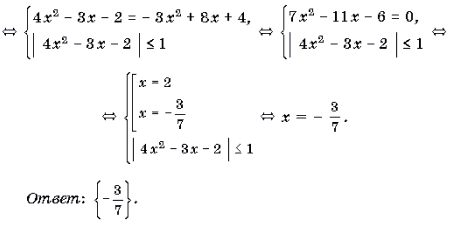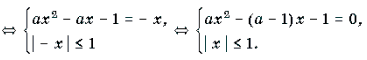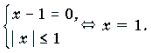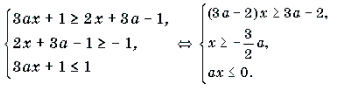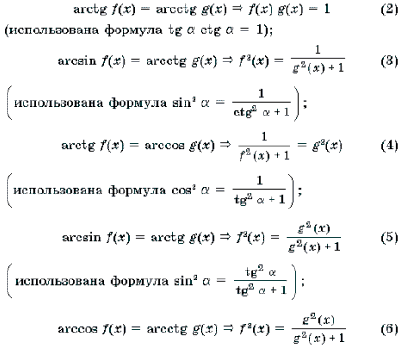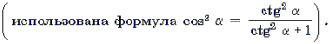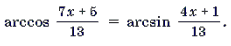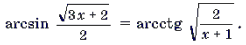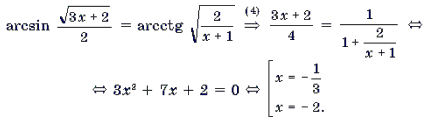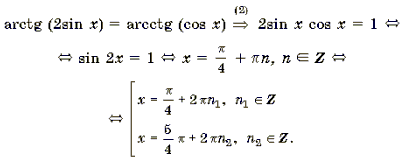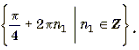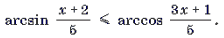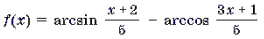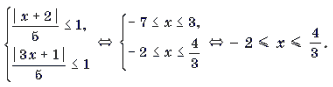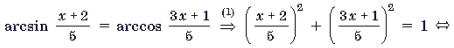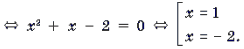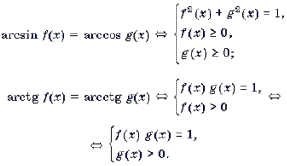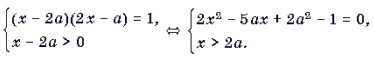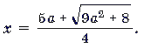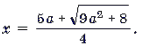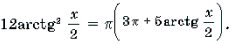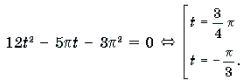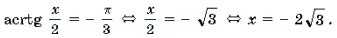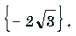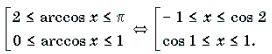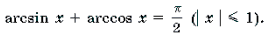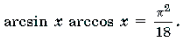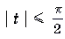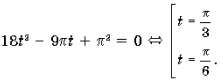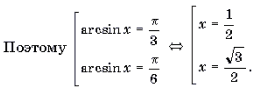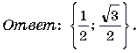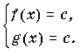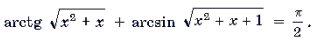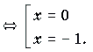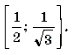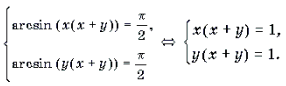Уравнения которые содержат обратные тригонометрические функции

Вначале напомним важнейшие свойства обратных тригонометрических функций.

1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];

arcsin (– x) = – arcsin x (x О [– 1; 1]);

2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];

3 Функция y = arctg x определена и монотонно возрастает на R;

arctg (– x) = – arctg x (x О R);

4 Функция y = arcctg x определена и монотонно убывает на R;

Свойства монотонности и ограниченности являются ключевыми при решении многих уравнений и неравенств, содержащих обратные тригонометрические функции. Перейдем к рассмотрению методов решения этих уравнений и неравенств.

I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями

Решение уравнений и неравенств, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность. Напомним, что функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения. Поэтому справедливы следующие равносильные переходы.

1 .

2 .

3 .

4 .

Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).

Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).

Решение. Уравнение равносильно системе

Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.

Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).

Решение. Неравенство равносильно следующему:

Пример 3. Решить неравенство 3arcsin 2x

Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).

Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .

Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:

arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

Рассмотрим два случая:

1) a = 0. В этом случае система примет вид:

2) a № 0. В этом случае уравнение системы является квадратным. Его корни:
Так как | x | Ј 1, то . Если a = – 1, то x₂ = x₁ = 1. Если a О (– Ґ Ч ; – 1) И [1; Ґ ), то уравнение имеет два корня.

Ответ : при при a = – 1 и a = 0 x = 1; при прочих a решений нет.

Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).

Решение. Неравенство равносильно системе

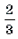
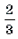
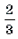
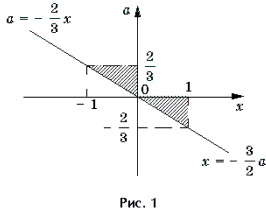
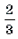
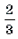
Решать последнюю систему можно графо-аналитическим методом, учитывая то, что при a > первое неравенство системы равносильно неравенству x і 1, при a – неравенству x Ј 1, при a = решением первого неравенства является любое действительное число. Множество всех точек (x; a) плоскости Oxa, удовлетворяющих системе, показано на рис. 1 штриховкой.

Ответ: при | a | > решений нет; при a = – x = 1;

II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями

При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Эта группа задач является чуть более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x₀ – решение этого уравнения. Обозначим arcsin f(x₀) = arccos g(x₀) через a. Тогда sin a = f(x₀), cos a = g(x₀), откуда f 2 (x₀) + g 2 (x₀) = 1. Итак, arcsin f(x) = arccos g(x) Ю f 2 (x) + g 2 (x) = 1. (1)

Рассуждая аналогично, можно получить следующие переходы:

Замечание 3. Корнем каждого из уравнений (1)–(4) может быть только такое число x₀, для которого f(x₀) і 0 и g(x₀) і 0. В противном случае множество значений левой и правой частей уравнения не пересекаются.

Пример 9. Решить уравнение

Корень является посторонним.

Пример 10. Решить уравнение

Корень x = – 2 является посторонним.

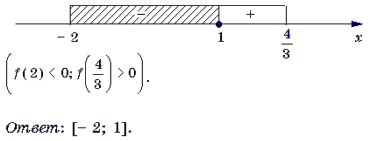
Ответ : .

Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).

Корни вида 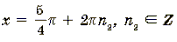являются посторонними.

Ответ :

При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций.

Пример 12. Решить неравенство

Решение. Рассмотрим функцию

и решим неравенство f(x) Ј 0 методом интервалов.

1) Найдем D(f). Для этого решим систему

2) Найдем нули f(x). Для этого решим уравнение

Корень x = – 2 является посторонним.

3) Решим неравенство f(x) Ј 0 методом интервалов.

Замечание 4. Заметим, что найдя корень уравнения можно было не обращаться к методу интервалов, а воспользоваться тем, что функция является монотонно возрастающей, а функция монотонно убывающей на отрезке . Поэтому решением исходного неравенства является промежуток [– 2; 1]. Следует, однако, понимать, что метод интервалов является более универсальным, – ведь его можно применять и в тех случаях, когда использование свойств монотонных функций не приводит к искомому результату.

При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,

Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).

Решение. Данное уравнение равносильно системе

Графиком квадратного трехчлена f(x) = 2x 2 – 5ax + 2a2 – 1 является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 2a. Это корень

Ответ: при любом a

III. Замена переменной

Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую замену переменной. При этом следует помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.

Пример 14. Решить уравнение

Решение. Обозначим 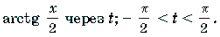После преобразований получим уравнение

Поскольку

откуда

Ответ :

Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.

Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда

Поскольку 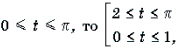откуда

Ответ : [– 1; cos 2] И [cos 1; 1].

Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Пример 16. Решить уравнение

Решение. Данное уравнение равносильно следующему:

Пусть arcsin x = t,

Тогда

IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций

Решение некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы.

Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.

Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.

Теорема 3. Если 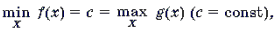то на множестве X уравнение f(x) = g(x) равносильно
системе

Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.

Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.

Пример 18. Решить уравнение

Решение. Пусть x 2 + x = t. Тогда уравнение примет вид

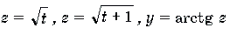
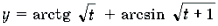
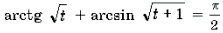
Функции являются монотонно возрастающими. Поэтому функция также является монотонно возрастающей. В силу теоремы 1 уравнение имеет не более одного корня. Очевидно, что t = 0 является корнем этого уравнения. Поэтому x 2 + x = 0

Пример 19. Решить неравенство

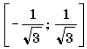
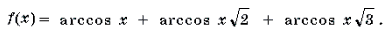
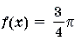
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке функцию Уравнение в силу теоремы 1 имеет не более одного корня. Очевидно, что – корень этого уравнения. Поэтому решением неравенства является отрезок

Ответ :

Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .

Решение. Поскольку arcsin 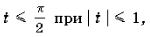то левая часть уравнения не превосходит Знак равенства возможен, лишь если каждое слагаемое левой части равно . Таким образом, уравнение равносильно системе:

Решение последней системы не представляет труда.

Уравнения и неравенства, содержащие обратные тригонометрические функции

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Обратные тригонометрические функции

Уравнения и неравенства

Задачи, связанные с обратными тригонометрическими функциями, часто вызывают у школьников старших классов значительные трудности. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как — то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике не излагается методика решения даже простейших уравнений и неравенств такого рода.

В данном материале уравнения и неравенства, содержащие обратные тригонометрические функции, по методам решения условно разделены на 4 группы, поэтому изложение материала производится в соответствии этого разбиения. Вначале перечислены основные свойства обратных тригонометрических функций и основные соотношения, которые используются при решении уравнений. В конце имеется набор упражнений для самостоятельной работы и приведены ответы.

Вначале напомним важнейшие свойства обратных тригонометрических функций.

Функция у = arcsin x

E(arcsin) = [- π /2;π /2]

arcsin 0 = 0, arcsin 1 = π /2,

является функцией нечетной, т.е.

arcsin(-x) = arcsin x; (| х |  1)

является функцией возрастающей

Функция у = arccos x

arccos 0 = π /2, arccos 1 = 0,

4) не является функцией ни четной, ни нечетной: arccos (-x) = π – arccos x; (|х |  1)

5) является функцией убывающей.

Функция у = arctg x

arctg 0 = 0, arctg  2/2 = π/4;

является функцией нечетной:

arctg (-x) = — arctg x;

является функцией возрастающей.

Функция у = arcctg x

Не является функцией ни четной, ни нечетной: arcctg(-x) = π – arcctg x

Является функцией убывающей.

sin(arcsin x) = x, при -1  x  1;

cos(arccos x) = x, при -1  x  1;

tg(arctg x) =x, при x  R

ctg(arcctg x) =x, при x  R

Формулы перехода к функциям другого наименования:

arcsin x = arccos = arctg x/ = arcctg /x, 0

arccos x = arcsin = arctg /x = arcctg x/ , 0

arctg x = arcsin x/ = arccos 1/ = arcctg 1/x, x>0

arcctg x = arcsin 1/ = arccos x/ = arctg 1/x, x>0

3. Основные тождества:

arcsin x + arccos x =π /2, при -1  x  1

arctg x + arcctg x = π /2 , при x  R

Применение метода замены переменной

Пример 1. Решить уравнение

2 arcsin 2 x – 7 arcsin x + 3 =0

Пусть arcsin x =t, | t |  π / 2

Откуда t = 3 или t = 1/2

Поскольку , | t |  π / 2 , то t = 1/2

Или arcsin x = 1/2 , x = sin1 / 2

Пример 2. Решить уравнение

arcsin 2 x + arccos 2 x = 5π 2 /36.

Пусть arcsin x =α, arccos x =β, | α |  π/2, 0  β  π;

По условию задания составим систему двух уравнений:

α 2 + β 2 = 5π 2 /36,

Решая, систему двух уравнений с двумя неизвестными получаем что, β = π /3 или β = π / 6

Или arccos x = π /3 или arccos x = π / 6

x = 1 / 2 или х =  3 / 2

Пример 3. Решить неравенство

arccos 2 x – 3 arccos x + 2  2

Решение. Пусть arccos x = t, 0  t  π. Тогда

Решая, квадратичное неравенство имеем:

Поскольку 0  t  π , то  2  t  π

Откуда  2  arccos x  π   — 1  x  cos 2

 0  arccos x  1  cos 1  x  1.

Ответ : [-1; cos 2]  [cos 1; 1].

Решить следующие уравнения методом замены переменной:

arcsin 2 x – π /2arcsin x + π 2 /18 = 0

arctg 2 x + arcctg 2 x = π 2 /8

6 arctg 2 x – 5 arctg x + 1 = 0

12 arctg 2 x/2 = π (3 π + 5 arctg x/2)

arcsinx  arccosx = π 2 /18

arctgx  arcctgx = -5π 2 /18

2. Уравнения и неравенства, содержащие одноименные обратные тригонометрические функции

Решение этих уравнений и неравенств основывается на таком свойстве обратных тригонометрических функций, как монотонность. Напомним, что функции y = arcsin x и y = arctg x монотонно возрастают, а функции y = arccos x и y = arcctg x монотонно убывают. Поэтому справедливы следующие равносильные переходы:

a) arcsin f(x) = arcsin g(x) 

б ) arcsin f(x)  arcsin g(x)   f(x)  -1,

а ) arccos f(x) = arccos g(x) 

б ) arccos f(x)  arccos g(x)   g(x)  -1,

3 . а ) arctg f(x) = acrtg g(x)  f(x) = g(x);

б ) arctg f(x)  arctg g(x)  f(x)  g(x).

4. а ) arcctg f(x) = accrtg g(x)  f(x) = g(x);

б ) arcctg f(x)  arcctg g(x)  f(x)  g(x).

Замечание. Какое из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: |f(x)|  1 (тогда используем первую систему), или |g(x) |  1 (в этом случае используем вторую систему).

Пример 10. Решить неравенство

2 arcsin x/2  π /3

arcsin x/ 2  π /6

arcsin x/ 2  arcsin 1/ 2

С учетом ОДЗ –2  х  1

Пример 11. Решить уравнение

arcsin (2x -15) = arcsin (x 2 — 6x — 8)

Учитывая, вышеприведенные равносильные преобразования имеем:

2х – 15 = х 2 – 6х – 8,   x 2 – 8x + 7 – 0, 

| 2x – 15|  1  | 2x – 15 |  1

Замечание. Решать неравенство, входящее в систему, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении уравнения 11.

Пример 12. Решить уравнение

arccos (4x 2 – 3x – 2) + arccos ( 3x 2 – 8x – 4) = π.

Решение. Так как π – arccos t = arccos (-t ), то имеет место следующая цепочка равносильных преобразований:

arccos ( 4x 2 – 3x – 2) = π – arccos ( 3x 2 – 8x – 4) 

arccos ( 4x 2 – 3x – 2) = arccos (-3x 2 + 8x + 4) 

 4x 2 – 3x – 2 = -3x 2 + 8x + 4,   7x 2 – 11x – 6 – 0,  |4x 2 – 3x – 2 |  1  |4x 2 – 3x – 2 |  1

Пример 13. Решить неравенство

arctg (5x 2 – 3x) > arctg (5x – 3).

Это неравенство равносильно неравенству:

( 5x 2 – 3x) > (5х – 3),

х (5х – 3) – (5х – 3) > 0,

Решение находится за корнями:

x > 1 или x  ; 0,6)  (1;  ).

Пример 14. Решить неравенство

arcsin (x 2 – x) > arcsin (3x – 4).

Это неравенство равносильно системе неравенств:

Решим первое неравенство системы:

Решим второе неравенство системы:

(1 —  5)/2  х  (1 +  5)/2.

Решим третье неравенство системы: х  1.

Объединяя, полученные результаты имеем

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 15. Решить уравнение с параметром а:

arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

arcsin (ax 2 – ax + 1) = — arcsin x 

 arcsin (ax 2 – ax + 1) = arcsin (-x) 

 ax 2 – ax + 1 = -1,   ax 2 – (a – 1)x – 1 = 0,

Рассмотрим два случая:

а =0. В этом случае система примет вид:

а  0. В этом случае уравнение системы является квадратным. Его корни: х₁ = 1 и х₂ = -1/a. Так как |x |  1, то | -1/a |  1  |a |  1. Если а = -1, то х₂ = х₁ = 1.

Если а  ( —  ; -1)  [1;  ), то уравнение имеет два корня.

Ответ: при а  (-  ; -1)  [1;  ) х = 1 и х = — 1/a;

при а = -1 и а = 0 х = 1;

при прочих а решений нет.

Решить следующие уравнения и неравенства:

16. 2 arccos x/2 ≥ π /2.

17. arccos (x 2 – 4x +3) > π /2.

18. arcsin (2x 2 – 9x +8 )/2 π /6

19. arcsin (5x – 3) π /3

20. arccos (3x + 2) = arccos ( 5x + 3).

21. arcctg (x 2 +2x) = arcctg (8x –5)

22. arccos (2x –1) arcsin (5x –3)

24. arctg x/2 + arctg x/3 = arctg x

3. Уравнения и неравенства, содержащие разноименные обратные тригонометрические функции.

При решении уравнений и неравенств данного вида пользуются известными тригонометрическими тождествами. Эта группа задач является более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Например, требуется решить уравнение

arcsin f(x) = arccos g(x).

Предположим, что х₀ – решение этого уравнения. Обозначим arcsin f(х₀) = arccos g(х₀) через α. Тогда sin α = f(х₀), cos α = g(х₀), откуда

arcsin f(x) = arccos g(x)  f 2 (х₀) + g 2 (х₀) = 1.

Пример 25. Решить уравнение:

arcsin 5x = arccos 12x

Решение. Используем формулу:

arcsin f(x) = arccos g(x)   f 2 (х₎ + g 2 (х) = 1,

Условия f(x)  0, g(x)  0 появляются так, как в противном случае, множество значений правой и левой частей уравнения не пересекаются.

Исходя, из вышеприведенной системы имеем:

(5х) 2 + (12х) 2 = 1,   25х 2 + 144 х 2 = 1, 

169х 2 = 1,  х = ± 1/13,

Пример 26. Решить неравенство

arccos x > arctg x.

Решение. Решим неравенство методом интервалов. Рассмотрим функцию f(x) = arccos x – arctg x и решим неравенство f(x) > 0. Областью определения этой функции является отрезок [-1;1]

Найдем нули функции: arccos x = arctg x

Используя формулу cos 2  = 1/(1 + tg 2  ) перейдем к системе:

x > 0; так как множество значений функций

y = arccos x и y = arc t g x совпадают при x > 0.

Решением первого уравнения системы будут значения х 2 = (  5 – 1)/2, но т.к. x > 0, то остается один нуль: х =  (  5 – 1)/2. Отметим его на координатной прямой:

Определим знаки в каждом интервале:

f(1) = arccos 1 – arctg 1 = — π /4

f(-1) = arccos(-1) – arctg(-1) = π + π /4 >0;

f(x) > 0 при -1  x  (  5 – 1)/2.

Пример 27. Решить уравнение

arcsin x = arccos(1 –2x).

Решение. Исходному уравнению равносильна система  sin(arcsin x) = sin(arccos(1 – 2x)),

Отсюда  х =  1 – (1 – 2х) 2 ,

Решить уравнения и неравенства:

28. arccos 4x = arcsin 3x;

29. arcsin x = arccos √1-x;

30. arcsin (x 2 – 2x) = arccos √1-x 2 ;

31. arcsin x = arcctg x;

Общий метод решения.

При решении уравнений и неравенств этого типа используются методы сведения их к алгебраическим. При их решении приходится использовать самые разные преобразования (которые могут быть не эквивалентными), поэтому необходимо сделать проверку каждого получившегося корня.

Пример 34. Решить неравенство

arcsinx ( π /2 – arcsin x )  0.

Решение. ОДЗ: | x |  1

Пусть arcsin x = t , | t |  π /2

Тогда неравенство перепишется

Данное неравенство равносильно совокупности:

С учетом условия | t |  π /2

-π/2  t  0, t = π /2

Вернемся к старой переменной:

— π /2  arcsin x  0, arcsin x = π/2

Пример 35. Решить уравнение

arccos x = 2 arctg (1 – x ).

Решение. ОДЗ: | x |  1

Обозначим arccos x через α , а arctg (1 – х) через β, тогда cos α = x , tg β = 1 – x . По условию задачи имеем систему:

Преобразуем второе уравнение системы:

Заменим tg  = t, тогда 1 – t 2 + t + t 3 – 1 – t 2 = 0,

t 3 – 2t 2 + t = 0,

 t = 0,   tg  = 0,   1 – x = 0,   x = 1,

 t = 1;  tg  = 1;  1 – x = 1;  x = 0.

Пример 36. Решить уравнение

arcsin (1 + 2 cos x ) + arccos (1 + 3 tg x ) = π /2.

Решение: Перепишем уравнение в виде:

arcsin(1 + 2cos x) = (π/2 — arccos(1 + 3tg x)),

Возьмем синусы обеих частей :

sin(arcsin(1 + 2cos x)) = sin(π/2 — arccos(1 + 3tg x)),

1 + 2cos x = 1 + 3tg x,

2 cos x – 3 tg x = 0,

2 cos 2 x – 3sin x = 0,

2 – 2 sin 2 x – 3sin x = 0,

2 sin 2 x + 3sin x – 2 = 0,

2 t 2 + 3 t – 2 = 0,

т.к. |t |  1, то t = 2 – посторонний корень,

следовательно t = 1/ 2;

x = 5π/6 + 2πn, n  Z

Проверка показывает, что серия корней

x = π/6 + 2πn, является посторонней.

Ответ: x = 5π/6 + 2πn, n  Z.

Решить уравнения и неравенства:

37. arcsin x = 2 arctg2x/3;

38. arcsin (x 2 – 3x + 0,5) = π /6;

39. arcsin (x 2 –2x +2) = π x /2;

40. arcsin 2x = 3 arcsin x;

41. arccos(x –1) = 2 arccos x;

42. arccos(3x – 4) = 2arctg(5 – 3x);

43. arcsin 2x + arccos(6x –2)  0;

В этом разделе представлены разные примеры, которые можно использовать как на уроках, так и при подготовке при поступлении в вузы.

Решить уравнение ( неравенство, систему).

44. arcsin ( x + 1) + arccos ( x – 1) = π /2;

45. arcsin(x + 1/x) + arctg(x 2 –1) = π/3;

46. arcsin 1/  x + arccos  (1-x) = π/2;

47. arcsin2x + arccos 2 x = π 2 /2;

48. arctg 3 x +arcctg 3 x = π 3 /24;

49. 3arctgx + 2arcctgx = π;

50. arcsin(1 – x) – 2arcsinx = π/2;

51. arctg(x 2 + 1) + arctg(x 2 –1) = π/4;

52. arcsin2x = 3arcsinx;

53. arctg(x –1)/x = 2arctg(x –1);

54. arcsin x + arcsin2x = π/2;

55.  arcsin x  arcsin y = π 2 /18,

 arccos x + arccos y = π/2;

56.  arcsin x + arccos y = π/2,

57.  arctg x + arctg y = π/3,

58.  arcsin x  arccos x = π 2 /18,

59.  arctg x  arcctg x = π 2 /16,

60.  arcctg x + arcctg y = π/2,

61. arcsin x > arcsin(1 — x);

62. arcsin(1 – x) + 2arcsin x > π/2;

63. arctg(x –1) + arctg x + arctg(x +) > arctg3x;

64. sin((arccos x)/5)= 1;

65. arctg(x 2 – 3x – 3) = -3π/4;

66. arctg(x + x 2 ) + arctg(x 2 – x) = π/4;

67. arctg3 x – arctg3 -x = π/6;

68. arccos (3ax + 1)  arccos(2x + 3a – 1);

69. arcsin x = arcsin(a 2 + a – 1)(x – 2a 2 – 3a +2);

Решение уравнений и неравенств, содержащих обратные тригонометрические функции

Уроки 1-2 в 10 академическом классе на тему

«Решение уравнений и неравенств,

содержащих обратные тригонометрические функции»

· Правильно определяет вид уравнения;

· Распознает уравнения, содержащие переменную под знаком обратной тригонометрической функции из множества уравнений других видов;

· Решает простейшие уравнения через определение «арктермина»;

· Определяет метод решения конкретного уравнения в знакомой ситуации;

· Решает более сложные уравнения знакомым методом: графическим, функционально-графическим, сведением к алгебраическому;

· Правильно выделяет уравнения, решаемые новыми методами: применением тождества, взятием удобной тригонометрической функции обеих частей уравнения, по свойствам монотонных функций;

· Определяет метод решения конкретного уравнения в знакомой ситуации;

· Решает неравенства знакомым методом: графическим, функционально-графическим.

· Знают вид уравнения;

· Умеют выделять уравнения из уравнений других видов;

· Применяют известные методы для решения уравнений с аркфункциями в знакомой ситуации.

Наглядные пособия и раздаточный материал:

— Раздаточный материал для диктанта;

— Презентация к уроку.

Урок изучения нового материала.

Частично-поисковый и проблемный.

1. Организационный момент и постановка целей.

2. Актуализация знаний через подготовку домашнего задания и постановку вопросов (с использованием презентации) на знание:

— определения обратных тригонометрических функций и «арктерминов»;

— некоторых свойств обратных тригонометрических функций;

— тождеств с обратными тригонометрическими функциями и способов их доказательства;

— алгоритмов решения уравнений и неравенств функционально-графическим методом;

— основных видов уравнений и неравенств;

— основных методов решения уравнений и неравенств.

2. Введение нового материала через проверку домашнего задания и постановку новой проблемы в этом задании, которая приведет к введению определения уравнения, содержащего переменную под знаком обратной тригонометрической функции.

3. Этап промежуточного контроля с целью выявления уровня усвоения метода решения простейших уравнений с проверкой с помощью презентации.

4. Изучение новых методов в новых ситуациях через сравнение с известными ситуациями из других тем методов решения уравнений.

5. Подведение итогов через рефлексию деятельности учащихся, оценку, самооценку и определение целей следующего урока. Задание на дом.

«Что значит решить задачу?

(советский математик, профессор МГУ,

Эпиграф урока: «Функция, как правило, определяется

для тех значений аргумента, какие для

данной задачи представляют реальное

I. На перемене до урока.

Просмотреть выполнение учащимися домашних работ. Вызвать к доске для оформления заданий 1-3 домашней работы трех учеников.

Задание №1. Доказать тождества (13), (20), (25);

Задание №2. Вывести из тождеств новые (учесть ОДЗ): (1, (18).

Задание №3 (Задание дома оформить на одной странице, вторую оставив свободной для последующих записей на уроке). Графически найти сумму координат точек пересечения графиков функций (а) ;

(б)

I этап. Организационный момент.

— (Учитель) Здравствуйте, ребята! Начинаем урок.

Чему мы научились с вами на прошлых уроках?

· (ученик) Изучили обратные тригонометрические функции, научились строить их графики, рассмотрели свойства;

· Научились вычислять значения обратных тригонометрических функций; сравнивать значения выражений;

· Вывели тождества, содержащие обратные тригонометрические функции, помогающие вычислениям значений функций или выражений.

— И чем планировали заниматься сегодня на уроке? Чему должны научиться?

· Сегодня мы познакомимся с уравнениями и неравенствами, содержащими обратные тригонометрические функции;

· Выведем формулы для решения простейших уравнений и неравенств;

· Попробуем использовать известные методы для решения уравнений и неравенств, содержащих аркфункции;

· Познакомимся с новыми специальными методами решения.

— Какие знания из нашего опыта попробуем применить? Определения арксинуса, арккосинуса, арктангенса и арккотангенса;

· Определения обратных тригонометрических функций;

· Тождества, содержащие тригонометрические функции;

· Методы решения уравнений и неравенств, основные и специальные.

— Какие умения будем использовать?

· Строить графики и их читать;

· Решать уравнения и неравенства известными методами.

— Итак, открыли тетради (напоминаю, страница с заданием №3 осталась свободной). Тема урока – «Решение уравнений и неравенств, содержащих обратные тригонометрические функции».

· (Работаем с презентацией)

Слайд 1(тема урока)

Слайд 3 (Эпиграф темы)

— Работаем устно. Какие функции называем обратными тригонометрическими функциями?

· (Слайд 5) Функции вида у=arcsin x, y=arccos x, y=arctg x, y=arcctg x называются обратными тригонометрическими функциями или аркфункциями.

— При формировании определения «arcsin a» что понимали под «а»? Под «arcsin a»?

· «а» — это число, «arcsin a» — это угол.

— Сформулируйте определения arcsin a, arccos a, arctg a, arcctg a.

· Арксинус числа — такой угол , синус которого равен а.

· Арккосинус числа — такой угол , косинус которого равен а.

· Арктангенс числа — такой угол , синус которого равен а.

· Арккотангенс числа — такой угол , котангенс которого равен а.

— Используя определения, найдите значения выражений (Слайд 8):

— Какие свойства арксинуса и арккосинуса можно использовать при вычислении в последних случаях?

· arcsin(-a)=-arcsin a; arccos(-a)=-a

— Какова связь между арксинусом и арккосинусом одного и того же числа?

— Используя определения, найдите значения выражений (Слайд 9):

— Какие свойства арктангенса и арккотангенса можно использовать при вычислении в последних случаях?

· arctg(-a)=-arctg a; arcctg(-a)=-a

— Какова связь между арктангенсом и арккотангенсом одного и того же числа?

— Итак, получили знакомые нам тождества. (Слайд 10) Имеют ли смысл выражения ?

· Первое, второе – нет, так как числа 2 и не входят в отрезок . Третье – имеет смысл, так как арктангенс определен на множестве всех действительных чисел.

— Может ли значение выражения быть равно 5, , -10?

· Углы в 5 и -10 радиан не входят в область значений ни одной аркфункции. Угол в радиан может быть значением арккосинуса числа, так как в данном случае .

— Найдите значения выражений (Слайд 11):

· Ответ: (учащиеся обосновывают

ответы. Если потребуется, то проговорить и показать в презентации свойства аркфункций, а именно (слайд 50):

— Проверяем домашнее задание.

Задание №1. Доказать тождества (13), (20), (25);

· (13)

Доказательство: , ч. т.д.

(20)

, ч. т.д.

(25)

Так как

При доказательстве каждого тождества можно использовать соотношения в прямоугольном треугольнике, с учетом знаков тригонометрических функций, например, докажем, что . Пусть arcsin x=, тогда sin =х, то есть отношение противолежащего катета к гипотенузе равно .

, найдем соs по теореме Пифагора (смотри рисунок). Тогда tg равен отношению противолежащего катета к прилежащему, то есть .

Задание №2. Вывести из тождеств новые (учесть ОДЗ): (13), (6), (18).

(13)

ОДЗ левой и правой частей равенства есть промежуток , . Пусть угол arcsin x=t, t . Имеем тригонометрическое уравнение tg t =,

t= , то есть .

(6) равносильно на ОДЗ .

(18) равносильно на ОДЗ .

II этап. Изучение нового материала.

Задание №3. Графически найти сумму координат точек пересечения графиков функций (а) ;

(б)

· Ответ (а): +1; (б) . (Учащиеся проверяют ответы задания в тетради).

— Работаем с решением (а).

— Что конкретно требовалось найти по условию задачи?

· Сумму соответствующих абсцисс и ординат точек пересечения графиков функций или сумму абсциссы и ординаты точки пересечения (если она единственная).

— Как мы поступали согласно требованиям задачи?

· В одной системе координат строили графики соответствующих функций, находили координаты их точек (точки) пересечения, находили сумму.

— А если бы требовалось найти абсциссу точки пересечения графиков, как можно было бы переформулировать задачу?

· Решить уравнение .

— Можно ли данное уравнение отнести к какому-либо известному виду?

— Перечислите, пожалуйста, известные вам виды уравнений.

— Какая, на ваш взгляд, функция могла бы определить вид данного уравнения?

— Действительно, данное уравнение – это уравнение, содержащее переменную под знаком обратной тригонометрической функции (Учитель акцентирует внимание учащихся на запись на доске темы урока, учащиеся записывают в тетрадях)

— Каким методом в данном случае мы его решили?

— Перечислите основные шаги этого метода применительно к данному уравнению.

— Заменим знак равенства на знак неравенства, например, (учитель цветным мелом на доске, а учащиеся цветной ручкой в тетради делают исправления). Какое неравенство по виду получили?

· Неравенство, содержащее переменную величину под знаком обратной тригонометрической функции.

— Решите его, используя предыдущее уравнение, и перечислите основные шаги графического метода решения неравенств. (Учитель приглашает желающего ученика к доске для комментария, учащиеся оформляют решение в тетради).

— Внимание, пример (б). Найдем абсциссу общих точек (точки) графиков функций. Ответ?

— Составьте уравнение, соответствующее этой задаче и определите его вид.

· , это уравнение, содержащее обратную тригонометрическую функцию.

— Можно ли было бы сразу оговорить количество корней уравнения? Почему?

· Да, не более одного корня, так как в левой части уравнения функция монотонно убывает на своей области определения, а в правой – возрастает.

— Можно ли было тогда обойтись без построения графиков при решении?

· Подобрать корень уравнения, используя функционально-графический метод.

— Проговорите и запишите решение на доске. (Ученик проговаривает решение данным методом и записывает, учащиеся записывают в тетрадях).

— Можно ли было этим методом решить уравнение (а)? Обоснуйте.

· Нет, так как функции, стоящие в обеих частях уравнения, имеют одинаковый характер монотонности (возрастающие).

— Меняем знак равенства на знак «>» и решаем полученное неравенство. Метод – функционально-графический. Можем ли мы использовать решение уравнения для решения неравенства и почему?

· Корень уравнения будет делить область определения (!) уравнения на промежутки, в каждом из которых монотонные функции, стоящие в обеих частях уравнения, будут сохранять постоянный знак. Нам останется только выбрать промежуток, на котором график левой функции лежит выше (л. ч. > пр. ч.) графика правой.

— Решим и прокомментируем запишем в тетради.

— Попробуйте решить функционально-графическим методом уравнение arcsin x =. (Слайд 17). Обоснуйте решение.

· Слева – возрастающая функция, справа – постоянная. Уравнение имеет не более одного корня. Находим подбором.

— А как проще решить уравнение?

· По определению: arcsin x – это угол, синус которого равен х, то есть x=sin() = -1.

— Составьте простейшие по виду уравнения с обратными тригонометрическими функциями, которые можно решать по определению.

— Итак, уравнения такого вида мы будем называть простейшими уравнениями, содержащими обратные тригонометрические функции.

Пользуясь определениями, составим формулы для решения уравнений (у каждого ученика на столе лежат заготовки, их дополняем. Ученики проговаривают, работает презентация).

(Слайд 18)

— Работаем устно. Решить простейшие уравнения по формулам или определению:

· (1) Нет решений, так как не входит в область значений арксинуса промежуток .

· (3) x =, так как 2х=tg=1.

· (4) x=0, так как =сtg =0.

III этап. Этап промежуточного контроля

— Проверим себя. Небольшой диктант (5-7 минут) по простейшим уравнениям, содержащим обратные тригонометрические функции. (У каждого ученика — листочки с текстом. Работаем на тех же листочках, вписывая решения). (Слайд 20).

— (Листочки собираем для проверки, предварительно ученики прописывают ответы себе в тетрадь). Проверим. Оценку за диктант можете себе предварительно выставить: 4 верных — «5», 3 верных – «4», 2 верных – «3», 1-0 – «2».

1 вариант 2 вариант

— Продолжаем работу. Итак, с какими по виду уравнениями мы познакомились?

· (Слайд 22, виды) С уравнениями, содержащими переменную величину под знаком обратной тригонометрической функции.

— Выберите из представленных уравнений те, которые можно отнести к этому виду. (К слайду 47).

· Это уравнения (4), (5), (6) из первого столбика и все уравнения из второго.

— Какие из них можно отнести к простейшим?

· Уравнения(2), (5) из первого столбика.

— Каким методом вы можете их решить?

· По определению (по формулам).

— Можете ли вы назвать корни второго уравнения?

IV этап. Изучение новых методов

— Пробуем решить другие уравнения. Какие методы решения мы можем попробовать применить?

(Внимание учащихся — на второй столбик)(Слайд 36 в презентации)

· функционально-графический и графический, по определению, оценка обеих частей уравнения, сведение к квадратному…

— Какие уравнения мы можем решить перечисленными методами?

(Ребята обязательно догадаются, как можно решить, например, уравнения (2) – к квадратному, (5) – использовать свойства аркфункций).

(Выявляем новые методы решения уравнений данного типа) Обратимся к простейшим (Слайд 19).

Второе уравнение arccos x =

— 1 подход: через определение: arccos x – это угол, косинус которого равен х, то есть x=cos() = 0.

— 2 подход: Что значит «решить уравнение?» — найти х…

— Где находиться х?

· Под знаком арккосинуса.

— Вспомните, как мы поступали, когда х был «спрятан», например, под знаком арифметического квадратного корня в уравнении вида и его нужно было «освободить».

· Возводили обе части уравнения в квадрат при условии, что правая часть неотрицательна, применяя свойство .

— Возможно ли выполнить соответствующие действия (как при решении иррационального уравнения) в данной ситуации?

· Можно применить свойство причем к обеим частям уравнения, то есть cos( arccos x) =cos , получим х=0.

— Говорят, «возьмем косинусы обеих частей уравнения» или «возьмем удобную тригонометрическую функцию обеих частей уравнения». Какие уравнения можно попробовать решить этим способом?

— Но где «опасность»?

· Посторонние корни. Нужно сделать проверку или найти ОДЗ уравнения.

— Осталось найти методы решения уравнений (6) и (13). Как поступим? Результаты какого из домашних заданий мы еще не использовали?

· Не использовали тождества. Например, в уравнении (13) одну из аркфункций можно выразить через другую, зная, что arcsinx+arccosx=.

— Какой прием применить?

— Или что применили?

— Можно ли, используя тождество, решить уравнение (6)? Если можно, то какое тождество применить?

· Тождество, полученное в домашней работе из тождества

(В процессе выявления методов учитель прописывает напротив каждого уравнения название метода решения)

Класс делится на 6 групп, каждой – по одному уравнению (повторить названия методов). 3 минуты решают на местах, по мере получения ответов выходят к доске представители групп и оформляют решение. Затем обсуждаем решения, каждый прописывает недостающее решение у себя в тетради, обязательно указывая метод решения.

Заключительный этап. Итоги урока и домашнее задание.

— Чем мы занимались сегодня на уроке, что нового узнали, чему научились?

· Определили вид уравнений с обратными тригонометрическими функциями, вывели формулы для решения простейших уравнений данного типа, установили возможность применения основных методов к решению уравнений, таких как графический, функционально-графический, по определению, с помощью замены, а также познакомились с новыми, специальными методами решения уравнений данного типа: «взять удобную тригонометрическую функцию обеих частей уравнения», применить тождество с обратными тригонометрическими функциями.

— Какой метод пока не рассмотрели в применении?

— Хорошо. Чем будем заниматься на следующих уроках?

· Отрабатывать умения распознавать необходимый для решения уравнения метод, непосредственно решать уравнения этим методом.

· От уравнений перейдем к неравенствам, выявим особенности их решения тем или иным методом.

— Молодцы! Домашнее задание. Используя «методички» (раздаются каждому ученику в качестве дидактического материала), решить уравнения I (1; 3; 4); II (1; 3; 7); V (2; 4). В группах уравнений I, II изменить знак равенства на любой знак неравенства и решить полученное неравенство. (Объявляются оценки за работу).

-Урок закончен. Спасибо за урок!

Уроки 3-4 в 10 академическом классе на тему

«Решение уравнений и неравенств,

содержащих обратные тригонометрические функции»

· Правильно определяет вид уравнения и неравенства;

· Распознает уравнения и неравенства, содержащие переменную под знаком обратной тригонометрической функции из множества уравнений и неравенств других видов;

· Решает простейшие уравнения через определение «арктермина» или взятием обратной тригонометрической функции обеих частей уравнения, решает простейшие неравенства соответственными методами с учетом характера монотонности функций;

· Распознает и определяет изученные методы решения более сложных конкретных уравнений и конкретных неравенств в знакомой ситуации;

· Решает уравнения и неравенства и уравнения с обратными тригонометрическими функциями и неравенства смешанного типа всеми известными методами.

· Знают виды уравнения и неравенства;

· Умеют выделять уравнения и неравенства из уравнений и неравенств других видов;

· Применяют известные методы для решения уравнений и неравенств с аркфункциями в знакомой ситуации.

Наглядные пособия и раздаточный материал:

— Презентация к уроку.

Тип урока: урок №3 комбинированный – урок закрепления знаний (по методам решения уравнений и некоторым методам решения неравенств), одновременного изучения нового материала (методы решения неравенств);

Урок №4 – урок обобщения и систематизации знаний.

1. Организационный момент и постановка целей.

2. Актуализация знаний через подготовку домашнего задания и постановку вопросов (с использованием презентации) на знание:

— определения уравнений и неравенств с обратными тригонометрическими функциями;

— алгоритмов решения простейших уравнений;

— алгоритмов решения уравнений и неравенств с аркфункциями методами: функционально-графическим, сведением к алгебраическому (метод интервалов для неравенств), с помощью тождеств;

— основных методов решения уравнений, рассмотренных на прошлом уроке и, соответственно, неравенств.

2. Отработка и закрепление изученного через проверку домашнего задания и практическую (индивидуальную, групповую работу на уроке), а именно: решение уравнений из списка с определением метода решения. Изучение нового материала (методы и приемы решения неравенств) через постановку новой проблемы («А как поступаем, если знак равенства поменять на знак неравенства?») в выполняемых заданиях по решению уравнений, которая приведет к получению знаний и приобретению навыков по решению неравенств с обратными тригонометрическими функциями.

3. Этап обобщения и систематизации методов решения уравнений и неравенств с обратными тригонометрическими функциями через рефлексию по выполненным упражнениям, дидактические материалы «Методы решения» и дидактические материалы, в которых метод решения не указан.

4. Подведение итогов через рефлексию деятельности учащихся, оценку, самооценку и определение целей следующего урока (урока контроля знаний). Задание на дом.

Наглядные пособия и раздаточный материал:

— Дидактические материалы «Методы решения», «Доказать тождества»;

— Презентация к уроку.

Замечания по содержательной части 3-4 уроков

1. На этапе актуализации знаний можно использовать слайды (18), (20) презентации, изменив численные значения.

2. Основные этапы прошлого урока также можно повторить, воспользовавшись презентаций («Что изучали на прошлом уроке?», «Что нового для себя открыли?»)

3. По слайду (23) повторить и обобщить основные и специальные методы решения уравнений и неравенств.

4. По слайдам (32), (33) повторить, а с помощью (34), (35) проверить решение уравнения и неравенства с помощью свойств монотонных функций.

5. Работу по основной части урока лучше начать со списка уравнений на доске, решаемых различными методами (учитель заранее выбирает из «методички»), распознавания метода их решения (и метода решения соответственного неравенства) с прописыванием на доске.

6. Формы работы (по группам, поочередно с выходом ученика к доске, самостоятельно за рабочим столом и последующей проверкой) учитель определяет, исходя и уровня подготовки класса, ситуации и своего видения хода урока.

7. Домашнее задание можно организовать как домашнюю самостоятельную работу (С-12, №6) по дидактическим материалам , , Алгебра и начала анализа 10-11, при этом самостоятельно превратив уравнение в неравенство (метод решения ученикам предлагается определить самостоятельно), либо по дидактическим материалам «Методы решения», где шаг определения метода уже не требуется (для менее подготовленных учащихся), либо по учебнику. Домашнюю работу можно дифференцировать, используя те же «методички», либо комбинировать источники заданий.

По тематическому планированию время на контрольную работу предусмотрено по всей теме «Обратные тригонометрические функции», поэтому проверочную самостоятельную работу можно провести на уроке-паре закрепления знаний и подготовке к контрольной работе, включив в нее, например, два уравнения и два неравенства, решаемые различными методами.

уравнений (неравенств), содержащих обратные тригонометрические функции

(Поменяйте знак «=» на знак и решите полученное неравенство)