Электронная библиотека
Областью в комплексной плоскости называется множество D точек этой плоскости, обладающее свойствами:
1) открытости – вместе с точкой из D этому множеству принадлежит и достаточно малая окрестность с центром в этой точке;
2) связности – любые две точки D можно соединить ломаной, целиком состоящей из точек D.
Примером области могут служить окрестности точек на комплексной плоскости. Под e-окрестностью точки z0 понимают открытый круг радиуса e с центром в этой точке: |z – z0| 2 + (y – 1) 2 = e 2 – окружность радиуса e с центром в точке х = 0, у = 1 комплексной плоскости.
Область с присоединенной к ней границей называют замкнутой и обозначают D. Будем в дальнейшем предполагать, что граница области состоит из конечного числа замкнутых линий, разрезов (дуг) и точек. Линии и разрезы, входящие в состав границы будем предполагать всегда кусочно-гладкими.
Область называется односвязной, если граница состоит из одной связной линии. Область называется многосвязной, если граница области состоит из нескольких связных частей, например: двухсвязной, трехсвязной и т.д. – по числу не связных между собой частей границы. На рис. 2.2,б – пример двухсвязной области.
Обход односвязной области считается положительным, если она остается по левую руку (контур обходится против хода часовой стрелки). На рис. 2.2,б сделан разрез l, а обход области изображен положительным (область в результате разреза стала односвязной).
Указать, является ли каждая из этих областей открытой или замкнутой, ограниченной или неограниченной, односвязной или многосвязной.
а) поэтому получим: . Область (рис. 2.3) – замкнутая, ограниченная, односвязная.
б) и – лучи, выходящие из начала координат (рис. 2.4). Все точки, удовлетворяющие неравенству б) лежат внутри угла, образованного этими лучами, и на сторонах этого угла. Следовательно, область замкнутая, неограниченная, односвязная.
Неравенство означает, что расстояние каждой точки z от точки больше 1, но меньше 2. Поэтому областью есть кольцо (его внутренность), ограниченное концентрическими окружностями с центром в точке . Область – открытая, ограниченная, двухсвязная (рис. 2.5).
г) Неравенство равносильно или
или, возведя в квадрат обе части, получим:
х 2 + у 2 – 2у + 1 2 + у 2 + 2у + 1.
Отсюда: – верхняя полуплоскость (рис.
Вывод: область у>0 – открытая, неограниченная, односвязная (рис. 2.4).
Определение. Кривая называется непрерывной, если она может быть задана параметрическими уравнениями:
в которых – непрерывные функции на отрезке .
Например, окружность ; дуга окружности
; дуга параболы – непрерывные кривые; гипербола не является непрерывной, так как функции эти при и имеют точки разрыва.
С помощью комплексного переменного параметрические уравнения кривой (2.18) можно записать в виде одного уравнения:
Например, уравнение эллипса с полуосями a и b можно записать:
уравнение окружности радиуса R
уравнение окружности с центром в точке запишется так:
Задачи для упражнений
1) Построить в комплексной плоскости линии, точки которых удовлетворяют уравнениям:
а) б) в) г) д) е) ж) ; з)
2) Построить на комплексной плоскости z области, заданные условиями:
Указать, является ли каждая из этих областей открытой или замкнутой, ограниченной или нет, односвязной или многосвязной.
3) Какие кривые определяются следующими уравнениями:
Ответы: а) б) в) г) д)
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
КОМПЛЕКСНОЗНАЧНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО. КРИВЫЕ НА КОМПЛЕКСНОЙ ОБЛАСТИ
Комплексные функции действительного переменного. Пусть каждой точке t отрезка [a,b] на действительной оси поставлено в соответствие число Z(t), если разложить число Z(t) на действительную и мнимую части Z(t)=х(t)+iy(t),то возникнут две действительные функции одного действительного переменного х(t) и y(t). Если эти функции непрерывны в точке 

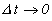

Справедливы и обратные утверждения.
Все правила вычисления производных вытекают из свойств пределов, поэтому
;
(с ― комплексное число);
;
, если
.
Здесь предполагалось, что 
Заметим еще, что для кусочно-непрерывной функции 



обладающий всеми свойствами обычного интеграла Римана.
Можно проверить, что комплексный постоянный множитель можно вносить под знак интеграла.
Вместо одного равенства интеграл можно эквивалентно определить двумя




Иными словами, знаки Re и Im можно вносить под знак интеграла.
Рассмотрим теперь модуль интеграла. Обозначим
Пусть 

I (cos 

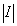




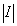
(постоянный множитель внесли под знак интеграла).
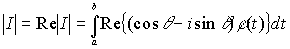
Действительная часть комплексного числа не превосходит его модуля, а определённый интеграл не меняет знака неравенства, поэтому

Отметим ещё, что справедлива формула Ньютона-Лейбница
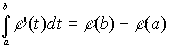
Кривые на комплексной плоскости. Непрерывное отображение отрезка 












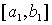


Совокупность всех взаимно эквивалентных путей называется кривой. Кривую мы обычно будем обозначать одной буквой, например, 


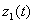


Кривая называется замкнутой, если её начало и конец совпадают. Понятие непрерывной кривой является слишком общим в том смысле, что оно не всегда соответствует нашему интуитивному понятию кривой. Так, например, построены кривые, множество точек которых совпадают с квадратом на плоскости (кривая Пеано). Более естественным объектом являются простые или жордановы кривые. Кривая называется простой или жордановой, если для её представителей (путей) 





Глубоким фактом является
Теорема Жордана. Всякая жорданова замкнутая кривая 

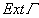
Доказательство этой теоремы сложно и здесь не приводится.
Для дальнейшего полезно следующее определение.
Область 


Геометрически понятие односвязности означает, что область «не имеет дыр». Если в области одна дыра, то она называется двусвязной и т.д.
Жордановы замкнутые кривые еще называют жордановыми контурами.
Путь 






Из курса анализа известно, что кусочно-гладкая кривая является спрямляемой, т.е. имеет конечную длину, вычисляемую с помощью интеграла по формуле
или в комплексной форме

Через 
http://mydocx.ru/10-83704.html

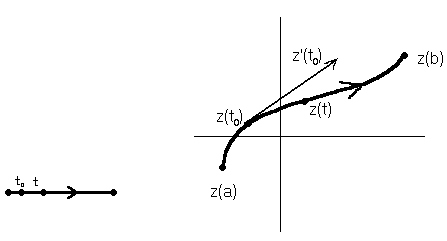
 ;
;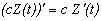 (с ― комплексное число);
(с ― комплексное число); ;
;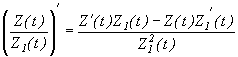 , если
, если  .
.









