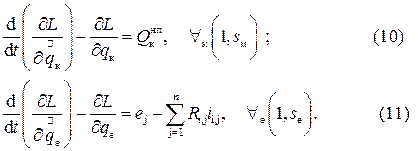Уравнения лагранжа для электромеханических систем

Жесткость C

Инверсная индуктивность Г

Кинетическая энергия

Энергия магнитного поля

Энергия электрического поля

Потенциальная энергия

Энергия электрического поля

Энергия магнитного поля

Мощность рассеяния

Мощность рассеяния

Мощность рассеяния

Первая система аналогий между механическими и электрическими цепями более «физична», поэтому в основном 6удем пользоваться ею, хотя в некоторых случаях применение второй системы дает более простые уравнения.

Из этой системы видно, что ЭДС в электрической цепи аналогична силе, индуктивность аналогична массе и обладает инерционностью, и энергия, запасаемая в магнитном поле, является кинетической энергией. Конденсатор, аналогично пружине, запасает энергию, которую логично считать потенциальной. Активное сопротивление действует аналогично механическому вязкому сопротивлению, и энергия, выделяемая на нем, рассеивается в виде тепла.

Тогда простейшей механической цепи, содержащей массу, пружину и вязкое сопротивление, и описываемой уравнением вида

можно поставить в соответствие простейшую электрическую цепь с последовательно включенными индуктивностью, емкостью и сопротивлением, описываемую уравнением

где L · q «- ЭДС самоиндукции, R · q `- падение напряжения на сопротивлении, S · q — напряжение на емкости.

В электротехнике обычно это уравнение записывается в виде:

Электромеханическую систему, имеющую S_m степеней механической свободы и S ₁ независимых электрических контуров, учитывая электромеханические аналогии, можно представить в виде механической системы, имеющей S_m + S ₁ степеней свободы и обладающей

• суммарной электромеханической кинетической энергией T_Σ = T_M + W_M ;
• потенциальной энергией П _Σ =П_М+ W _Э ;
• мощностью рассеяния D_Σ = D_M + D _Э .

Отсюда движение в такой системе будет описываться уравнениями, аналогичными уравнениям Лагранжа и называемыми уравнениями Лагранжа-Максвелла :

,

Первые S_m уравнений описывают механические движения в системе (механические уравнения), последующие S ₁ уравнений описывают процессы в электрических цепях (электрические уравнения — уравнения 2-го закона Кирхгофа).

1.3. Энергия электрического и магнитного полей. Силы и моменты, возникающие при электромеханическом преобразовании энергии

В общем виде энергия электрического поля в объеме V выражается интегралом

,

где E — вектор напряженности электрического поля, D — вектор смещения.

Для однородного поля в конденсаторе

Энергия магнитного ноля в объеме V также выражается интегралом

где B — вектор магнитной индукции, H — вектор напряженности магнитного поля.

Для однородного магнитного поля

Для n магнитно связанных контуров с токами получим:

,

где L_jk — индуктивности и взаимные индуктивности контуров

Или , где Y _j — потокосцепление контуров.

Тогда для одиночного контура с током имеем:

для двух контуров: ;

для контура с током, помещенного в магнитный поток Φ: ,

где L — индуктивность контура, Y — потокосцепление внешнего потока F с контуром.

Рассмотрим гипотетическую электромеханическую систему. в которой механически связаны контур с током, помещенный в магнитное поле, и ротор конденсатора, причем при повороте происходит изменение индуктивности контура, потокосцепления с контуром и емкости конденсатора.

Общая кинетическая энергия такой системы будет:

;

;

Подставляя это выражение в уравнение Лагранжа-Максвелла и принимая за обобщенную координату h — угол поворота f , а также считая, что внешняя сила отсутствует, получим два уравнения — механическое и электрическое

Из первого (механического) уравнения получаем силы (в данном случае — моменты), возникающие при электромеханическом преобразовании энергии :

• — сила (момент), вызванная изменением индуктивности от изменения координаты (угла поворота) — злектромагнитная сила,
• — сила (момент), действующая на проводник (контур) с таком, помещенный в магнитный поток,- магнитоэлектрический момент,
• — сила (момент), вызванная электрическим полем при механическом изменении емкости конденсатора .

Реально в технике применяются преобразователи, в которых действует только одна из перечисленных сил — электромагнитные, магнитоэлектрические, электростатические.

Слагаемые второго, электрического уравнения являются электрическими реакциями системы:

• — противоЭДС, вызванная изменением индуктивности при повороте контура с током (если индуктивность изменяется, что происходит не всегда);
• — ЭДС индукции, вызванная вращением контура в магнитном поле;
• — ЭДС самоиндукции;
• — напряжение конденсатора;
• R · i — падение напряжения на сопротивлении.

Эквивалентная схема электрической цепи такой системы имеет вид на .

Рис. 1-1. Эквивалентная схема гипотетической электромеханической системы

1.4. Электромагнитные, электродинамические и электростатические преобразователи.

1.4.1. Электромагнитные преобразователи.

В электромагнитном преобразователе усилие создается за счет изменения магнитной энергии, запасенной в катушке индуктивности L при перемещении сердечника. Магнитная и энергия и энергия рассеяния имеют следующий вид:

,

В этих системах , поэтому дифференциальные уравнения имеют вид (при отсутствии внешней силы):

;

Типичным преобразователем такого типа является электромагнитное реле, схема которого приведена на .

Рис. 1-2. Электромагнитное реле.

Реле представляет собой электромагнит с контактами К. При подаче напряжения U на обмотку электромагнита, имеющую индуктивность L и активное сопротивление R создается электромагнитное тяговое усилие , которое притягивает якорь Р, изменяя его положение относительно сердечника 1 (координату h от 0 до d ), при этом происходит переключение контактов К.

Из анализа дифференциальных уравнений имеем:

• m · h «- сила инерции,
• r · h `- сила вязкого сопротивления, которой в реле можно пренебречь,
• c · h — сила сопротивления возвратной пружины ВП, имеющей жесткость С,
• — тяговое усилие,
• — ЭДС, вызванная изменением индуктивности при перемещении якоря,
• — ЭДС, вызванная изменением тока,
• R · i — падение напряжения на активном сопротивлении обмотки реле.

Итак, тяговое усилие реле определяется изменением индуктивности L при перемещении якоря. При показанной на конструкции реле (клапанного типа) и малом перемещении якоря можно считать, что

.

Тогда , откуда , где .

При включении репе на постоянное напряжение, как эта обычно бывает, процесс описывается нелинейными дифференциальными уравнениями:

, где

Тогда так называемые тяговые характеристики реле имеют вид на .

Рис. 1-3а. Механические характеристики электромагнитного реле

Характеристики вход-выход имеют скачкообразный характер ( ).

Рис. 1-3б. Характеристики «вход-выход» электромагнитного реле.

Переходный процесс при включении реле показан на .

Рис. 1-4. Переходный процесс при включении реле.

Модель электромагнитного реле приведена в .

1.4.2. Электродинамические преобразователи.

В магнитоэлектрической (электродинамической) системе усилие создается за счет изменения второй составляющей магнитной энергии Y (h) × i . То есть уравнения имеют следующий вид:

;

Электродинамический принцип преобразования энергии используется в электроизмерительных приборах, содержащих постоянный магнит, двигателях постоянного тока, тахогенераторах постоянного тока. В этих устройствах обобщенной характеристикой является угол поворота ротора f и уравнения имеют вид:

;

Обычно обозначают угловую частоту вращения , тогда

;

• — момент сопротивления, вызванный механической инерционностью системы ( I — момент инерции системы),
• ρ·ω- момент вязкого сопротивления,
• σ· f — момент упругого сопротивления,
• — вращающий момент,
• M_c — статический момент сопротивления,
• — ЭДС индукции (вращения),
• — ЭДС самоиндукции,
• R · i — падение напряжения на активном сопротивлении.

При применении преобразователя как исполнительного устройства (измерительного прибора) используется факт возникновения магнитоэлектрического вращающего момента, пропорционального току в цепи ротора. При применении его как датчика скорости используется возникновение в цепи ЭДС индукции, пропорциональной частоте вращения ротора. В этом случае электрическое уравнение преобразователя имеет вид :

И в установившемся режиме, когда , имеем .

В частности, при повороте в магнитном поле с индукцией B рамки длиной 1 и радиусом r имеем dΨ = r ·ω· B ·1· r · d f , откуда .

Основным достоинством электродинамических систем является линейность их характеристик.

1.4.3. Электростатические преобразователи.

В электростатических системах используется энергия электрического поля, запасенная в конденсаторе

;

В этом случае дифференциальные уравнения таковы:

;

Здесь — тяговое усилие, S × q — напряжение на конденсаторе .

Эти уравнения имеют меньше слагаемых, чем уравнения индукционных систем, поэтому электростатические преобразователи обладают меньшими возможностями и получили меньшее распространение.

Исполнительные устройства электростатического типа очень маломощны, так как электрическое поле в единице объема может сконцентрировать гораздо меньше энергии, чем магнитное. Поэтому тяговое усилие сравнительно небольшое. Исполнительные устройства такого типа применяются в основном как измерительные и индикаторные.

Возможности электростатического преобразователя как датчика, как видно из электрического уравнения, также ограничены, так как он не может индуцировать ЭДС и является, по существу, пассивным емкостным датчиком с уравнением вида:

Обозначив U_c — напряжение на конденсаторе, получим :

Пассивный емкостной преобразователь переменного тока.

1.5. Классификация электромеханических преобразователей

Электромеханические преобразователи, применяемые в системах автоматики и вычислительной технике, можно классифицировать по назначению, конструктивному исполнению и принципу действия (см. ).

Рис. 1-5. Классификация электромеханических преобразователей.

1.6. Представление электромеханических преобразователей как преобразователей сигналов (информации)

При применении электромеханических преобразователей в системах автоматического управления они рассматриваются не как энергетические устройства, а как информационные преобразователи сигналов при их прохождении от входов к выходам (см. ).

Рис. 1-6а. Функциональная схема динамической системы.

Если электромеханический преобразователь описывается исходными линейными или линеаризованными дифференциальными уравнениями, то от них можно перейти к дифференциальным уравнениям «вход-выход» вида

где y ( t ) и u ( t ) — векторы выходных и входных координат

; — полиномиальные матрицы,

— оператор дифференцирования по времени.

Перейти от исходных энергетических уравнений к уравнениям «вход-выход» удобно, используя структурные схемы и передаточные функции. Типичная структурная схема имеет вид, представленный на , где W ( p ) — передаточные функции, а u ( p ), y ( p ), i ( p ) — изображения входных, выходных и внутренних переменных ( p = c + j·ω ).

Рис. 1-6б. Структурная схема динамической системы.

Уравнение «вход-выход» получим в виде:

,

где

Структурная схема тесно связана с физикой работы преобразователя и поэтому легко может быть составлена по исходным энергетическим уравнениям, а уравнения «вход-выход» представляют более абстрактную модель системы.

Можно перейти к еще более абстрактной модели — уравнениям состояния, когда система представляется стандартной структурой в виде автомата с памятью ( ).

Рис. 1-7а. Структурная схема динамической системы в виде непрерывного автомата.

;

,

где x — вектор состояния, A — матрица коэффициентов, B — матрица управления, C — матрица выхода, D — матрица обхода.

В этой структуре переменные состояния часто не являются физическими величинами, которые могут быть измерены в реальной системе.

Для моделирования электромеханической системы на ЭВМ или при управлении ею от ЭВМ удобно эту систему представить как дискретную по времени (импульсную), в которой ее переменные наблюдаются (вычисляются) через дискретные промежутки времени Т. При выборе Т достаточно малом по сравнению с инерционностью системы, дискретная модель достаточно точно описывает непрерывную систему.

Для анализа дискретной модели вводится аппарат дискретного преобразования Лапласа и дискретные передаточные функции D ( Z ), где Z — оператор запаздывания на интервал Т .

При достаточно малом Т можно принять .

Имея передаточную функцию системы W ( P ), заменой получим D ( Z ) в виде

,

где Z -1 — запаздывание на один такт (время Т). Этой функции соответствует разностное уравнение «вход-выход»

Этой модели соответствует дискретный рекурсивный фильтр вида , где А и В -полиномиальные матрицы, а Т — матрица задержек тактов.

Рис. 1-7б. Структурная схема динамической системы в виде дискретного автомата.

По схеме рекурсивного фильтра может быть восстановлен алгоритм вычисления выходной величины y ( n ) в данном такте, зная y ( n — i ) в предыдущие такты, и значения входного воздействия u ( n ) в данный такт и u ( n — i ) в предыдущие такты — прямое программирование. Применяются также последовательное и параллельное программирование, когда D ( Z ) представляется в виде произведения или суммы более простых функций.

От разностных уравнений «вход-выход» можно перейти к уравнениям пространства состояний и представить систему в виде дискретного автомата с памятью в виде .

;

где x[n] — состояние в данный такт, x[n+1] — состояние в следующий такт.

Удобной моделью для анализа динамической системы является частотная характеристика

которая обычно представляется в виде двух характеристик, амплитудной A (ω) и фазовой f (ω).

1.7. Анализ простейшего электромеханического преобразователя.

Рассмотрим простейший магнитоэлектрический преобразователь, имеющий одну степень механической н электрической свободы, в качестве которого может быть приведен линейный исполнительный двигатель, применяемый в системе позиционирования в накопителях на жестких дисках СМ-ЭВМ.

Его динамика описывается двумя уравнениями:

Модель такого преобразователя приведена на и .

Обозначив и , получим эти уравнения в операторной форме:

Перейдя к изображениям, получим следующие уравнения:

По этим уравнениям можно получить структурную схему согласно , по которой можно получить передаточную функцию

где ; ;

Рис. 1-8. Структурная схема электромеханического преобразователя.

Перейдя обратно во временную область, можно получить уравнение «вход-выход»

, где

Для перехода к уравнениям состояния представим уравнение вход-выход в скобочной форме

Введем новые координаты, соответствующие перемещенным в квадратных скобках и получим дифференциально-алгебраическую систему (слева) и ее преобразованную форму (справа)

Этим уравнениям соответствует структура, показанная на .

Рис. 1-9. Структурная схема преобразователя в пространстве состояния.

При переходе к уравнениям состояния получим x `= A · x + B · u ; h = C · x + D · u ,

где u = U ; ; ; ; ; D =0.

При достаточно малом периоде квантования Т по сравнению с инерционностью системы ее можно представить как дискретную (по времени) с дискретной передаточной функцией

Произведя необходимые преобразования, получим

где ; ; B ₁ = B ₂ =3· B ₀ ; B ₃ = B ₀ .

Обозначим h `= h · K ₀ -1 .Тогда из выражения получим разностное уравнение «вход-выход»:

Этому уравнению соответствует структура рекурсивного фильтра, представленная на .

Рис. 1-10а. Структурная схема преобразователя в виде рекурсивного фильтра.

Используя, например, прямое программирование, можно моделировать систему на ЭВМ, вычисляя значения выходной величины h ( n ) по шагам. Скажем, переходную функцию при ступенчатом воздействии

U ( n )= U при n >0 (см. )

Рис. 1-10б. Выход преобразователя при ступенчатом воздействии.

От разностного уравнения вход-выход можно перейти к уравнениям состояния и представить систему в виде дискретного автомата с памятью

;

• X ( n ) — вектор состояния автомата в данный дискретный момент времени,
• X ( n +1) — вектор состояния в следующий наблюдаемый момент через промежуток времени Т,
• B — матрица входного преобразования,
• A — матрица, реализующая функцию переходов,
• C — матрица, соответствующая функции выходов.

Частотная характеристика системы

В этом случае, если характеристическое уравнение имеет вещественные отрицательные корни, получим

Тогда амплитудная частотная характеристика будет (см. )

Рис. 1-11. Частотная характеристика электромеханического преобразователя.

1.8. Упражнения и контрольные вопросы к главе 1.

1. Перечислите основные механические аналогии, дополнив колонки 1 и 2 таблицы 1-1 размерностями представленных в них физических величин.
2. Выведите уравнения динамики простейших механической и электромеханической систем из уравнений Лагранжа-Максвелла. Нарисуйте схемы, соответствующие этим уравнениям.
3. Перечислите основные типы электромеханических преобразователей и приведите примеры этих преобразователей.
4. Выведите передаточную функцию и нарисуйте структурную схему линейного двигателя без пружины и без трения.
5. По полученной в п.4 передаточной функции выведите выражение для частотной характеристики двигателя и постройте ее, задавшись численными значениями параметров двигателя (например, Тэ=10 мс, m=50 г, Кэм=0,05 Вс).

Уравнения Лагранжа-Максвелла 2 рода

Уравнения Лагранжа — Максвелла – универсальны и справедливы для любой системы координат. Форма уравнения Лагранжа – Максвелла не зависит от физической природы параметров.

Представим систему уравнений 2-го рода применительно к электромеханической системе в полном объеме

Уравнение (10) справедливо для всех степеней свободы механической подсистемы от 1 до s_м , а уравнение (11) справедливо для всех степеней свободы электрической подсистемы от 1 до s_е.

Эти уравнения записаны на энергетическом уровне.

Для электромеханической системы функция Максвелла имеет вид

где Т_м – кинетическая энергия механической подсистемы;

Т_е – кинетическая энергия электрической подсистемы;

П_м – потенциальная энергия механической подсистемы;

П_е– потенциальная энергия электрической подсистемы.

– кинетическая энергия для линейного характера поступательного движения, где m – масса объекта,υ – линейная скорость перемещения объекта;

– кинетическая энергия для вращательного движения, где J_xк – момент инерции к– ой точки относительно оси, проходящей через центр вращения;

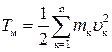
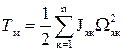
Ω_xк– угловая скорость вращения к– ой точки.

сумма потенциальных энергий всех материальных точек.

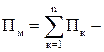
Кинетическая энергия электрической подсистемы – это энергия магнитного поля подсистемы.

(13)

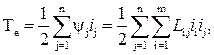
где Ψ_j – потокосцепление; i – ток , j – количество контуров; L_i,j – индуктивность, если i=j, то это собственная индуктивность; если i≠j, то это взаимная индуктивность; i_i, i_j – токи соответствующих контуров.

Потенциальная энергия электрической подсистемы – это энергия электрического поля.

(14)

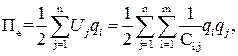
В выше приведенной системе уравнений Лагранжа – Максвелла используются так называемые обобщенные координаты q, которые однозначно определяют положение или состояние системы.

q_к – обобщенная координата механической подсистемы.

q_j – обобщенная координата электрической подсистемы.

Обычно в качестве обобщённой координаты выбирается та координата, которая уже не дробится на другие.

Введем также понятие число степеней свободы s:

s_м – число степеней свободы механической подсистемы;

s_e– число степеней свободы электрической подсистемы, определяет количество выделенных независимых контуров.

В уравнениях Лагранжа – Максвелла применяется также понятие «связи». Связи – это условия, определяющие свободу перемещений точек системы.

Связи могут быть кинематическими и аналитическими, представленными в форме

где Ψ – потокосцепление , C – ёмкость, М – взаимоиндуктивность, L – индуктивность.

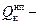
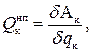
Введенное выше обозначение означает обобщённые силы, не связанные с потенциальной энергией, т.е. «не потенциальные силы». Размерность обобщённой не потенциальной силы может не совпадать с размерностью силы физической .

(15)

где А_к – элементарная работа, q_к – обобщенная координата механической подсистемы.

δА_к – определяется как работа всех активных сил на возможном перемещении.

(16)

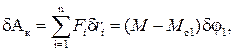
где δr_i– возможные перемещения материальных точек. Возможные перемещения — это перемещения, вызываемые изменениями обобщённых координат.

нп – обобщённые силы, не связанные с потенциальной энергией.

е_j – это ЭДС в независимых координатах.

R_i,j – активные cопротивления в j – ых независимых контурах, по которым протекает соответствующий ток.

Теоретическая механика. Уравнения Лагранжа

В этой статье мы попробуем разобраться с такой темой, как «Уравнения Лагранжа». Вообще, уравнения Лагранжа довольно полезная штука, например, на их основе решаются задачи на малые колебания. В МГТУ им. Баумана в третьем семестре предлагается самостоятельное домашнее задание, в котором нужно записать уравнения Лагранжа для системы с двумя степенями свободы.

Итак, типовое задание выглядит так.

Прежде чем броситься решать эту задачу, посмотрим на задание и проанализируем его. Есть призма 3, которая движется поступательно по горизонтальной плоскости без трения. В призме сделан паз 2, по которому движется шарик 1. Если вы помните темы прошлого семестра, то легко увидите, что шарик совершает сложное движение — переносное поступательное вместе с призмой 3 и относительное поступательное по пазу 2. Далее есть стержень 4, который соединяет призму и каток 5. Очевидно, что скорость центра катка С равна скорость призмы. Каток движется без скольжения, это важный момент. Движение системы описывается двумя обобщенными координатами, которые любезно выбрал для нас составитель задания.

Итак, приступим к решению.

Поскольку обобщенных координат две (две степени свободы), система уравнений Лагранжа будет выглядеть так:

Расчет начинаем с записи уравнений связи — выражаем скорости всех ключевых точек и тел, имеющих массу, через обобщенные координаты. Из сказанного ранее понятно, что нам понадобится линейная скорость призмы 3, линейная скорость катка 5, угловая скорость катка 5 и скорость шарика 1. С поступательным движением все просто

С угловой скоростью катка тоже все понятно. Так как проскальзывание отсутствует

Самое трудное — выразить скорость шарика 1. Как мы уже говорили, он совершает сложное движение, значит, его скорость складывается из относительной и переносной. Переносная — это скорость поступательного движения призмы 3. Относительное — скольжение вдоль паза 2, которое описано координатой S. Значит

Векторно складываем эти две скорости

Второе выражение здесь — это теорема косинусов. Если нанести все векторы на рисунок, станет понятно, почему так.

Определившись со скоростями, записываем выражение для кинетической энергии системы Т. Полная кинетическая энергия складывается из кинетических энергий всех тел, обладающих массой. То есть в нашем случае, тел 1, 3, 5.

Шарик 1 обладает энергией

Призма 3 движется поступательно

Каток 5 совершает плоское движение, так что его кинетическая энергия складывается из энергии поступательного и вращательного движений

Полная кинетическая энергия системы

Для записи уравнений Лагранжа это выражение нужно несколько раз продифференцировать.

Сначала по координате x. Частные производные

Производную по x с точкой дифференцируем по времени

Теперь то же самое по координате S. Частные производные

Производная по времени

Левая часть уравнений Лагранжа готова. Займемся правой частью. Для нее нужно посчитать обобщенные силы по каждой координате. Есть несколько способов это сделать, мы предпочитаем делать это через элементарную работу на малом приращении координаты. В общем случае формула выглядит так

На практике это применяется следующим образом. Сначала нанесем на рисунок все действующие силы. В нашем случае это сила упругости пружины и силы тяжести.

Сначала считаем обобщенную силу по координате x. Для этого мысленно «замораживаем» координату S, и позволяем системе свободно двигаться по координате x. То есть шарик «приклеивается» к пазу 2, и внутри него никуда не движется. Все перемещение происходит по координате x. Очевидно, что сила упругости работу не совершает, так как ее длина не меняется. Очевидно, что силы тяжести работу не совершают, так как движение происходит горизонтально. Официальным языком это записывается так

Теперь обобщенная сила по координате S. Мысленно «замораживаем» координату x. Получается, что призма 3 вместе с пазом 2 и катком 5 стоит на месте, а внутри неподвижного паза движется шарик. Сила упругости совершает работу, также как и сила тяжести шарика 1. Пружина была растянута на величину статической деформации δ и дополнительно растянута на S в произвольный момент времени, то есть сила упругости равна с·(δ+S). Работа силы упругости отрицательна, так как пружина растягивается. Работа силы тяжести шарика 1 положительна, так как шарик движется вниз. Силы тяжести призмы 3 и катка 5 работу не совершают, так как эти тела покоятся. Получаем

Собственно, все. Собираем все посчитанные величины в уравнения Лагранжа и получаем систему дифференциальных уравнений, описывающих движение системы.

Для проверки можно посмотреть размерности, в обеих частях выражения размерности должны совпадать (обычно это ньютоны).

Конечно, разные задачи немного отличаются в ходе решения, но алгоритм всех задач примерно такой.

1) Определить число степеней свободы и выбрать обобщенные координаты

2) Записать уравнения связей

3) Записать выражение для кинетической энергии

4) Взять необходимые производные

5) Записать обобщенные силы по каждой координате

6) Записать уравнения Лагранжа

Если что-то не получается, не отчаивайтесь, мы всегда рады помочь.