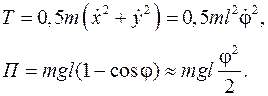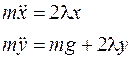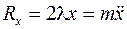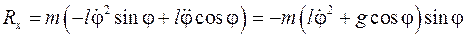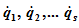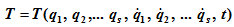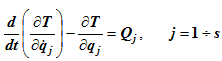Уравнения лагранжа i и ii рода

ЛАГРА́НЖА УРАВНЕ́НИЯ

ЛАГРА́НЖА УРАВНЕ́НИЯ ме­ха­ни­ки, обык­но­вен­ные диф­фе­рен­ци­аль­ные урав­не­ния вто­ро­го по­ряд­ка, опи­сы­ваю­щие дви­же­ние ме­ха­нич. сис­тем под воз­дей­ст­ви­ем при­ло­жен­ных к ним сил. Вы­ве­де­ны Ж. Ла­гран­жем в 1788 в двух фор­мах: Л. у. 1-го ро­да – урав­не­ния в де­кар­то­вых ко­ор­ди­на­тах с не­оп­ре­де­лён­ны­ми мно­жи­теля­ми Ла­гран­жа, и Л. у. 2-го ро­да – урав­не­ния в обоб­щён­ных ла­гран­же­вых ко­ор­ди­на­тах.

Лекция 10. Уравнения Лагранжа 1-го рода

Применяются при решении специальных задач. Прежде всего, их можно применить для определения реакций идеальных связей при движении системы. Достоинством уравнений Лагранжа 2-го рода является отсутствие в них реакций идеальных связей, что существенно облегчает задачу динамики и, вообще, делает ее разрешимой. Найти реакции идеальных связей в этом случае можно способом, основанным на применении принципа освобождаемости от связей. Сначала решается задача по определению законов изменения обобщенных координат, в которой реакции идеальных связей не учитываются. Затем механическая система разнимается по связям, реакции которых необходимо найти. Составляются уравнения Лагранжа 2-го рода для полученных в результате разъема связей частей системы. Туда подставляется найденное ранее решение и таким образом находится значение реакций связей.

Получим уравнения Лагранжа 1-го рода.

Имеем МС с l идеальными связями, уравнения которых

(10.1)

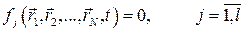
Отсюда, в соответствии с тем, что при варьировании время не меняется, а операция варьирования совпадает с операцией дифференцирования, получим

(10.2)

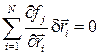
Умножим (10.2) на λ_j и сложим, получим

(10.3)

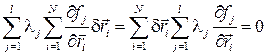
В то же время по свойству идеальности связей

(10.4)

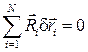
где 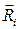‑ реакции идеальных связей.

Вычтем из уравнения (10.3) уравнение (10.4), получим

(10.5)

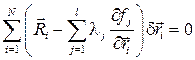
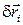
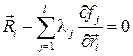
Среди 3N вариаций независимых вариаций будет только столько, сколько степеней свободы у МС, т.е. s. Остальные 3N—s , т.е. l будут зависимыми и выражаются через независимые из (10.2). Поэтому подберем значения коэффициентов λ_j так, чтобы выражения в скобках, куда они входят в уравнении (10.5), обращались в ноль. Остальные 3N—l=s скобок обязаны равняться нулю, т.к. при них стоят независимые вариации, а сумма (10.5) равна нулю при любых значениях этих вариаций. Таким образом, все скобки в выражении (10.5) равны нулю

.

Откуда, находятся все силы реакций идеальных связей

.

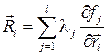
Запишем теперь уравнения движения всех точек системы, исходя из ІІ закона Ньютона

(10.6)

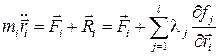
Это и есть уравнения Лагранжа I рода.

В этих 3N уравнениях 3N+l неизвестных, поэтому к ним следует добавить l уравнений связей (10.1).

Рассмотрим пример малых движений математического маятника (рис. 8.1а).

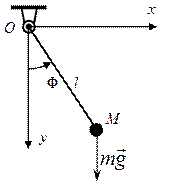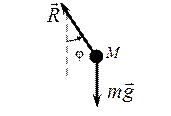Выбрав за обобщенную координату угол поворота оси невесомой нити от вертикали φ, получим

Тогда, согласно уравнениям Лагранжа 2-го рода (5.1), получим

. (10.7)

. (10.8)

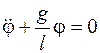
Теперь разрежем нить (освободим точку М от связи) и составим уравнение для точки М, движущейся под действием силы тяжести и силы натяжения нити (рис. 10.1б). Проектируем уравнение движения точки в форме 2-го закона Ньютона на нормаль, получаем

,

. (10.9)

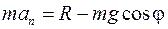
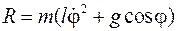
Для одновременного получения закона движения механической системы и действующих в ней реакций связей и служат уравнения Лагранжа 1-го рода.

Составим уравнения движения математического маятника в форме уравнений Лагранжа 1-го рода

(10.10)

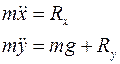
Выразим проекции силы реакции связи через неопределенные множители Лагранжа

, ,

, ,

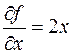
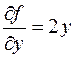
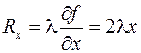
получим уравнения (10.10) в виде

Найдем из первого 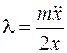, подставим во второе, получим

. (10.11)

Это уравнение решается заменой

, . (10.12)

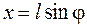
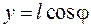
получим уравнение (10.7). Но, одновременно,

.

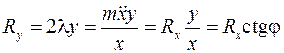
После подстановки в первое уравнение заменяющей формулы (10.12) и уравнения (10.7), окончательно, получим

,

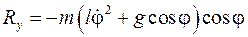
iSopromat.ru

Уравнения Лагранжа второго рода, которые представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат.

Для такой системы можно записать s уравнений, которые называются уравнениями Лагранжа второго рода или дифференциальными уравнениями движения в обобщенных координатах:

Уравнения Лагранжа второго рода могут быть обобщены на случай связей, осуществляемых с трением, хотя они и не являются идеальными. Для этого следует силу трения перенести из группы сил реакции в группу активных сил, тогда связь с трением можно формально считать идеальной.

Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат q₁, q₂,…q_s.

Дважды интегрируя эти уравнения и определяя по начальным условиям постоянные интегрирования, получим систему уравнений движения в обобщенных координатах:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах