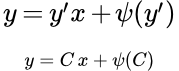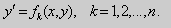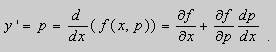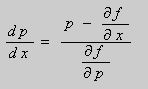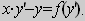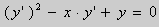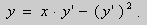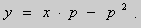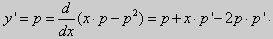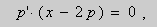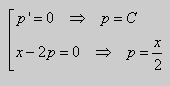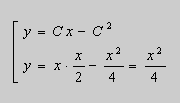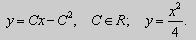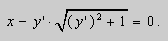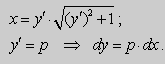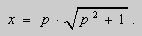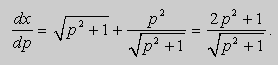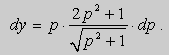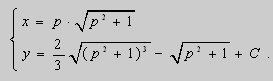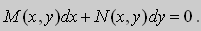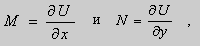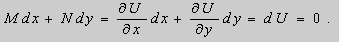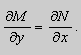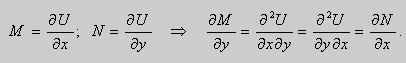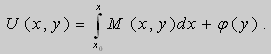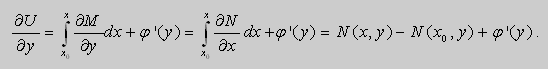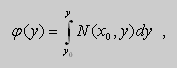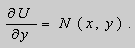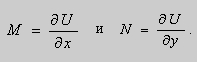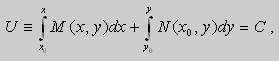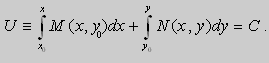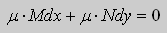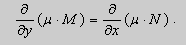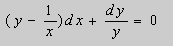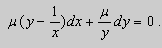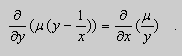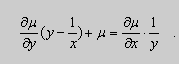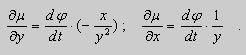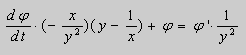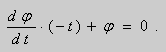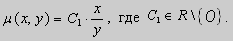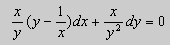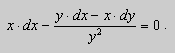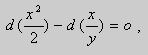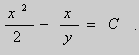Уравнения лагранжа и клеро на примерах

Дифференциальное уравнение Клеро

Решение дифференциального уравнения Клеро

Рассмотрим уравнение Клеро:
(1)
Не трудно убедиться, что его общее решение имеет вид:
(2)

Действительно, поскольку – постоянная, то – тоже постоянная. Тогда дифференцируя (2) имеем:
;
(3) .
Подставляя (2) и (3) в (1), получаем тождество:
.

Особое решение дифференциального уравнения Клеро

Уравнение Клеро может иметь особое решение. Как известно, если общее решение дифференциального уравнения имеет вид:
,
то особое решение может получиться исключением из уравнений:
;
.

В нашем случае, решение (2) можно записать в виде:
.
Тогда
.
Тогда особое решение может получиться, исключением из уравнений:
;
.

Поскольку возможны посторонние решения, то после нахождения особого решения, необходимо проверить, удовлетворяет ли он исходному уравнению (1).

Пример

Решить уравнение:
(1.1)

Это уравнение Клеро. Его общее решение имеет вид:

Ищем особое решение. Перепишем общее решение в виде:
.
Дифференцируем по :

.
Тогда особое решение может получиться исключением из уравнений:
(1.2) ;
(1.3) .

Исключаем . Из уравнения (1.3) имеем:
(1.4) .
Возводим в квадрат и преобразуем:
;
;
. Отсюда следует, что .
Извлекаем квадратный корень:
(1.5) .
Поскольку мы возводили в квадрат, то, возможно, (1.5) содержит лишние решения, которые не удовлетворяют (1.4). Сейчас мы примем (1.5), а отсев лишних решений сделаем в самом конце.
Подставим (1.4) и (1.5) в (1.2):
.

Итак, особые решения имеют вид:
(1.6) .
Теперь сделаем проверку, чтобы выяснить, удовлетворяет ли исходному уравнению (1.1):
(1.1) .
Находим производную (1.6) и выполняем преобразования:

;
;
.
Подставляем в (1.1):
(1.7) .

При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять нижний знак:
.
То есть при , .

При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять верхний знак:
.
То есть при , .

Общее решение уравнения имеет вид:

При уравнение имеет особое решение:
.

При уравнение имеет особое решение:
.

Автор: Олег Одинцов . Опубликовано: 24-08-2012 Изменено: 10-04-2016

Лекция 2. Дифференциальные уравнения первого порядка, не разрешённые относительно производной .

Рассмотрим уравнение вида

F ( x , y , y ‘ ) = 0 ,

не разрешённое относительно производной. Если попытаться выразить из него y ‘ , то можно получить , вообще говоря , несколько уравнений

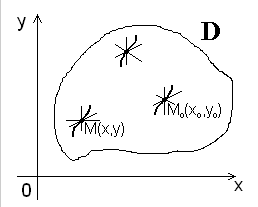
Геометрически это означает , что в каждой точке 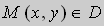задаётся несколько направлений поля (см.рис.2).

Следовательно через любую точку M ( x , y ) может проходить несколько интегральных кривых 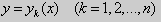. Для того, чтобы выделить из этого множества единственную интегральную кривую, проходящую через заданную точку M₀ ( x₀ , y₀) , надо помимо значений ( x₀ , y₀ ) дополнительно задать в этой точке направление поля y ‘ ( x₀) = y ‘_{0 .}

Задача Коши . Найти решение 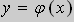уравнения F ( x , y , y ‘ ) = 0, удовлетворяющее начальным условиям y ( x₀) = y₀ и y ‘ ( x₀) = y ‘₀ , где y ‘₀ — решение уравнения F ( x₀ , y₀ , y ‘ ) = 0.

Теорема существования и единственности решения задачи Коши.

Пусть в некоторой окрестности U точки (x₀ , y₀ , y ‘₀ ), где y ‘₀ — решение уравнения F ( x₀ , y₀ , y ‘ ) = 0, выполнены условия :

1) F( x , y , y ‘ ) определена, непрерывна и имеет непрерывные частные производные F’_y и F’_{y ‘} по совокупности переменных ( x , y , y ‘ ) ;

2) значение производной F_y‘_‘ (x₀ , y₀ , y’₀ )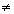0.

Тогда в некоторой окрестности точки x₀ существует единственное решение 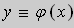уравнения F (x, y, y’) = 0, удовлетворяющее условиям y(x₀) = y₀ и y’ (x₀) = y’₀ .

Метод введения параметра.

На практике при решении уравнений F( x , y , y ‘ ) = 0 часто используют следующий метод.

Предположим , что уравнение F( x , y , y ‘ ) = 0 “легко” решить относительно y : y = f ( x , y ‘ ). Тогда введем замену y ‘ = p ( параметр зависит от x ). Предполагая, что дифференциальное уравнение имеет решение y = y ( x ) , получим ( в силу уравнения )

Из этих равенств выражаем :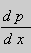

Это уравнение разрешено относительно производной 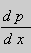. Пусть его общее решение имеет вид p = p ( x , C ) .Тогда общее решение заданного уравнения можно записать в виде y =f ( x , p ( x , C ) ). Решение найдено.

Таким методом можно решать , в частности , уравнения Лагранжа и Клеро.

Уравнение вида 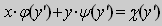называется уравнением Лагранжа. Оно является линейным относительно переменных x и y . Частным случаем этого уравнения является уравнение Клеро. Оно имеет вид :

Пример 1 . Решить уравнение

Решение. Выразим из уравнения (5) переменную y :

.Заменим 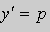и получим

Продифференцируем его по x :

Из этих равенств получаем :

После подстановки этих выражений в (6) будем иметь

Ответ :

Этим методом можно также решать уравнения , в которых «легко» выражается переменная x . Рассмотрим

Пример 2 . Решить уравнение

Решение . Выразим из уравнения (7) переменную x и введём параметр p :

Продифференцируем уравнение (8) по p :

Отсюда в силу равенства dy = p dx получим :

Проинтегрируем это уравнение :

Таким образом , с учётом ( 8 ) , получаем общее решение в параметрическом виде :

Примеры. Решить уравнения :

Уравнения в полных дифференциалах.

Если в уравнении (9) функции

В этом случае уравнение (9) называют уравнением в полных дифференциалах. После интегрирования получим общее решение уравнения

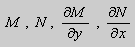
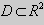
Теорема 1. Пусть функции непрерывные в некоторой односвязной области . Тогда необходимым и достаточным условием того, что уравнение (9) — в полных дифференциалах , является условие

Доказательство. 1. Необходимость.

Если выбрать функцию 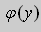та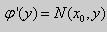к, чтобы

то и , следовательно ,

Таким образом , в уравнении (9)

Теорема 1 доказана.

Из теоремы следует , что общее решение уравнения (9) можно записать в виде

если 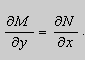Функцию U можно также представить в виде

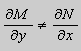
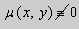
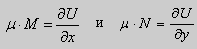
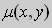
Предположим , что . Тогда можно попытаться найти такую функцию , чтобы . Функция называется интегрирующим множителем . В этом случае мы получаем уравнение

в полных дифференциалах. Следовательно, в силу теоремы 1,

Это уравнение позволяет найти интегрирующий множитель. Рассмотрим

Пример. Решить уравнение

Решение. Простой проверкой убеждаемся , что (10) не является уравнением в полных дифференциалах. Умножим его на неизвестную функцию :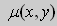

Попробуем найти 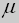из уравнения :

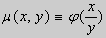
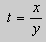
Пусть . Обозначим через и получим

После подстановки этих выражений в (11) будем иметь :

Проинтегрируем полученное уравнение :

Таким образом, интегрирующий множитель можно взять в виде

Умножим теперь уравнение (10) на функцию

Теорема 2. Если функции M и N непрерывные , имеют непрерывные частные производные первого порядка по x и по y , и 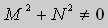, то интегрирующий множитель существует.

Замечание. Точка ( x₀ , y₀ ), в которой M ( x₀ , y₀ ) = N ( x₀ , y₀ ) = 0 является особой точкой уравнения (9). Поведение решений в окрестности особой точки изучается в лекции 3.

Примеры. Решить дифференциальные уравнения :

Примеры выполнения отчета по практике

Уравнения Лагранжа и Клеро.

( Алекси Клод Клеро (1713 – 1765) французский математик ин. поч. член Петерб. АН )

Определение. Уравнением Лагранжа называется дифференциальное уравнение, линейное относительно х и у, коэффициенты которого являются функциями от y ’ .

Для нахождения общего решение применяется подстановка p = y ’ .

Дифференцируя это уравнение, c учетом того, что , получаем:

Если решение этого (линейного относительно х) уравнения есть то общее решение уравнения Лагранжа может быть записано в виде:

Определение. Уравнением Клеро называется уравнение первой степени (т.е. линейное) относительно функции и аргумента вида:

Вообще говоря, уравнение Клеро является частным случаем уравнения Лагранжа.

С учетом замены , уравнение принимает вид:

Это уравнение имеет два возможных решения:

или

В первом случае :

Видно, что общий интеграл уравнения Клеро представляет собой семейство прямых линий.

Во втором случае решение в параметрической форме выражается системой уравнений:

Исключая параметр р, получаем второе решение F ( x , y ) = 0. Это решение не содержит произвольной постоянной и не получено из общего решения, следовательно, не является частным решением.

Это решение будет являться особым интегралом.

Далее рассмотрим примеры решения различных типов дифференциальных уравнений первого порядка.

Пример. Решить уравнение с заданными начальными условиями.

Это линейное неоднородное дифференциальное уравнение первого порядка.

Решим соответствующее ему однородное уравнение.

Для неоднородного уравнения общее решение имеет вид:

Дифференцируя, получаем:

Для нахождения функции С(х) подставляем полученное значение в исходное дифференциальное уравнение:

Итого, общее решение:

C учетом начального условия определяем постоянный коэффициент C .

Окончательно получаем:

Для проверки подставим полученный результат в исходное дифференциальное уравнение: верно

Ниже показан график интегральной кривой уравнения.

Пример. Найти общий интеграл уравнения .

Это уравнение с разделяющимися переменными.

Общий интеграл имеет вид:

Построим интегральные кривые дифференциального уравнения при различных значениях С.

С = — 0,5 С = -0,02 С = -1 С = -2

С = 0,02 С = 0,5 С = 1 С = 2

Пример. Найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.

Это уравнение с разделяющимися переменными.

Общее решение имеет вид:

Найдем частное решение при заданном начальном условии у(0) = 0.

Окончательно получаем:

Пример. Решить предыдущий пример другим способом.

Действительно, уравнение может быть рассмотрено как линейное неоднородное дифференциальное уравнение.

Решим соответствующее ему линейное однородное уравнение.

Решение неоднородного уравнения будет иметь вид:

Тогда

Подставляя в исходное уравнение, получаем:

Итого

С учетом начального условия у(0) = 0 получаем

Как видно результаты, полученные при решении данного дифференциального уравнения различными способами, совпадают.

При решении дифференциальных уравнений бывает возможно выбирать метод решения, исходя из сложности преобразований.

Пример. Решить уравнение с начальным условием у(0) = 0.

Это линейное неоднородное уравнение. Решим соответствующее ему однородное уравнение.

Для линейного неоднородного уравнения общее решение будет иметь вид:

Для определения функции С(х) найдем производную функции у и подставим ее в исходное дифференциальное уравнение.

Итого

Проверим полученное общее решение подстановкой в исходное дифференциальное уравнение.

(верно)

Найдем частное решение при у(0) = 0.

Окончательно

Пример. Найти решение дифференциального уравнения

с начальным условием у(1) = 1.

Это уравнение может быть преобразовано и представлено как уравнение с разделенными переменными.

С учетом начального условия :

Окончательно

Пример. Решить дифференциальное уравнение с начальным условием у(1) = 0.

Это линейное неоднородное уравнение.

Решим соответствующее ему однородное уравнение.

Решение неоднородного уравнения будет иметь вид:

Подставим в исходное уравнение :

Общее решение будет иметь вид:

C учетом начального условия у(1) = 0:

Частное решение:

Пример. Найти решение дифференциального уравнения с начальным условием у(1) = е.

Это уравнение может быть приведено к виду уравнения с разделяющимися переменными с помощью замены переменных.

Обозначим :

Уравнение принимает вид :

Получили уравнение с разделяющимися переменными.

Сделаем обратную замену:

Общее решение:

C учетом начального условия у(1) = е:

Частное решение:

Второй способ решения.

Получили линейное неоднородное дифференциальное уравнение. Соответствующее однородное :

Решение исходного уравнения ищем в виде:

Тогда

Подставим полученные результаты в исходное уравнение:

Получаем общее решение:

Пример. Решить дифференциальное уравнение с начальным условием у(1)=0.

В этом уравнении также удобно применить замену переменных.

Уравнение принимает вид :

Делаем обратную подстановку:

Общее решение:

C учетом начального условия у(1) = 0:

Частное решение:

Второй способ решения.

Замена переменной :

Общее решение:

III. Дифференциальное исчисление функции одной переменной

17. Производная функции, ее геометрический и механический смысл. Производная суммы, произведения и частного (обзор теорем школьного курса).

18. Производная сложной функции. Производная обратной функции. Производные обратных тригонометрических функций. Функции, заданные параметрически, и их дифференцирование.

19. Гиперболические функции, их свойства и графики. Производные гиперболических функций.

20. Дифференцируемость функции. Дифференциал функции. Связь дифференциала с производной. Геометрический смысл дифференциала. Дифференциал суммы, произведения и частного. Инвариантность формы дифференциала.

21. Производные и дифференциалы высших порядков. Формула Лейбница.

IV. Исследование функций с помощью производных

22. Условия возрастания и убывания функции. Точки экстремума. Необходимые условия экстремума. Достаточные признаки существования экстремума. Отыскание наибольшего и наименьшего значений непрерывной на отрезке функции.

23. Исследование функции на экстремум с помощью производных высшего порядка. Исследование функций на выпуклость и вогнутость. Точка перегиба. Асимптоты кривых. Общая схема построения графиков функций.

24. Комплексные числа. Их изображение на плоскости. Модуль и аргумент комплексного числа. Алгебраическая, тригонометрическая и показательная формы комплексного числа. Операции над комплексными числами. Формула Муавра.

25. Многочлен в комплексной области. Теорема Безу.

26. Корни многочлена. Основная теорема алгебры. Разложение многочлена с действительными коэффициентами на линейные и квадратичные множители.

27. Комплексные функции действительного переменного. Их дифференцирование. Формула Эйлера.

Базисы на плоскости и в пространстве Определение 1. Совокупность любых двух линейно независимых векторов, принадлежащих данной плоскости, называется базисом на этой плоскости. Если , — базис на плоскости, то для любого вектора , лежащего в этой плоскости, можно найти единственным образом такие числа и , что будет . Числа и называются координатами вектора в данном базисе.