ДВИЖЕНИЕ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ ОТСЧЕТА
Страница 1 из 2
До сих пор, рассматривая движение любой механической системы, мы всегда относили его к инерциальной системе отсчета. Только в инерциальных системах отсчета функция Лагранжа, например, одной частицы во внешнем поле имеет вид
L0 =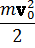 
− U, (39.1)
и соответственно уравнение движения
m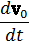 
= − 
(мы будем в этом параграфе отличать индексом 0 величины, относящиеся к инерциальной системе отсчета).
Займемся теперь вопросом о том, как выглядят уравнения движения частицы в неинерциальной системе отсчета. Отправным пунктом при решении этого вопроса снова является принцип наименьшего действия, применимость которого не ограничена никаким выбором системы отсчета; вместе с ним остаются в силе и уравнения Лагранжа
= 
. (39.2)
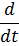
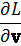
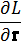
Однако функция Лагранжа уже не имеет вида (39.1), и для ее нахождения необходимо произвести соответствующее преобразование функции L0.
Это преобразование мы произведем в два приема. Рассмотрим сначала систему отсчета K’, которая движется относительно инерциальной системы K0 поступательно со скоростью V(t). Скорости v0 и v‘ частицы относительно систем K0 и K’ связаны друг с другом соотношением
v0 = v‘ + V(t). (39.3)
Подставив это выражение в (39.1), получим функцию Лагранжа в системе K’
L’ =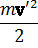 
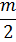
+ mv‘V + 
V 2 − U.
Но V 2 (t) есть заданная функция времени; она может быть представлена как полная производная по t от некоторой другой функции, и потому третий член в написанном выражении может быть опущен. Далее, v‘=dr‘/dt, где r‘ — радиус-вектор частицы в системе координат K’; поэтому
mV(t)v‘ = mV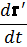
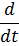
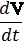
= (mVr‘) − mr‘ 
.
Подставив это в функцию Лагранжа и снова опустив полную производную по времени, получим окончательно:
L’ =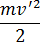 
− mW(t)r‘ −U, (39.4)
где W=dV/dt — ускорение поступательного движения системы отсчета K’.
Составляя с помощью (39.4) уравнение Лагранжа, получим
m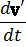 
= − 
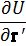
− mW(t). (39.5)
Мы видим, что в смысле своего влияния на уравнения движения частицы ускоренное поступательное движение системы отсчета эквивалентно появлению однородного силового поля, причем действующая в этом поле сила равна произведению массы частицы на ускорение W и направлена в противоположную этому ускорению сторону.
Введем теперь еще одну систему отсчета, K, которая имеет общее с системой K’ начало, но вращается относительно нее с угловой скоростьюΩ(t); по отношению же к инерциальной системе K0 система K совершает как поступательное, так и вращательное движение.
Скорость v‘ частицы относительно системы K’ складывается из ее скорости v относительно системы K и скорости [Ωr] ее вращения вместе с системой K:
v‘ = v + [Ωr]
(радиус-векторы r и r‘ частицы в системах K иK’‘ совпадают). Подставив это выражение в функцию Лагранжа (39.4), получим
L =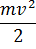 
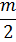
+ mv[Ωr] + [Ωr] 2 − mWr − U. (39.6)
Это есть общий вид функции Лагранжа частицы в произвольной неинерциальной системе отсчета. Отметим, что вращение системы отсчета приводит к появлению в функции Лагранжа члена совершенно особого вида — линейного по скорости частицы.
В классической механике представления о силах и их свойствах основываются на законах Ньютона и неразрывно связаны с понятием инерциальная система отсчёта.
Действительно, физическая величина, называемая силой, вводится в рассмотрение вторым законом Ньютона, при этом сам закон формулируется только для инерциальных систем отсчёта [17] . Соответственно, понятие силы оказывается определённым только для таких систем отсчёта [18] .
Уравнение второго закона Ньютона, связывающее ускорение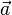 
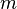
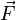
и 
массу материальной точки с действующей на неё силой 
, записывается в виде
Из уравнения непосредственно следует, что причиной ускорения тел являются только силы, и наоборот: действие на тело не скомпенсированных сил обязательно вызывает его ускорение.
Третий закон Ньютона дополняет и развивает сказанное о силах во втором законе.
Учёт содержания всех законов Ньютона приводит к заключению о том, что силы, о которых идёт речь в классической механике, обладают неотъемлемыми свойствами:
· сила есть мера механического действия на данное материальное тело других тел. [19]
· в соответствии с третьим законом Ньютона силы способны существовать лишь попарно, при этом природа сил в каждой такой паре одинакова [20][21] .
· любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, силы обязательно представляют собой результатвзаимодействия тел [22] .
Никакие другие силы в классической механике в рассмотрение не вводятся и не используются [18][23] . Возможность существования сил, возникших самостоятельно, без взаимодействующих тел, механикой не допускается [22][24] .
Хотя в наименованиях эйлеровых и даламберовых сил инерции содержится слово сила, эти физические величины силами в смысле, принятом в механике, не являются
Ньютоновы силы инерции[править | править вики-текст]
Некоторые авторы используют термин «сила инерции» для обозначения силы-противодействия из третьего закона Ньютона. Понятие было введено Ньютоном в его«Математических началах натуральной философии» [26] : «Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает свое состояние покоя или равномерного прямолинейного движения. От инерции материи происходит, что всякое тело лишь с трудом выводится из своего покоя или движения. Поэтому врожденная сила могла бы быть весьма вразумительно названа силою инерции. Эта сила проявляется телом единственно лишь, когда другая сила, к нему приложенная, производит изменение в его состоянии. Проявление этой силы может быть рассматриваемо двояко — и как сопротивление, и как напор.», а собственно термин «сила инерции» был, по словам Эйлера, впервые употреблён в этом значенииКеплером( [26] , со ссылкой на Е. Л. Николаи).
Для обозначения этой силы-противодействия некоторые авторы предлагают использовать термин «ньютонова сила инерции» во избежание путаницы с фиктивными силами, применяемыми при вычислениях в неинерциальных системах отсчёта и при использовании принципа д’Аламбера.
Отголоском ньютоновского выбора слова «сопротивление» для описания инерции является также представление о некоей силе, якобы реализующей это свойство в форме сопротивления изменениям параметров движения. В связи с этим Максвелл заметил, что с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, так как сладким он становится не сам по себе, а лишь после добавления сахара [26] .
Существование инерциальных систем отсчёта[править | править вики-текст]
Ньютон исходил из предположения, что инерциальные системы отсчёта существуют и среди этих систем существует наиболее предпочтительная (сам Ньютон связывал её с эфиром, заполняющим всё пространство). Дальнейшее развитие физики показало, что такой системы нет, но это привело к необходимости выйти за пределы классической физики.
Движение в инерциальной СО[править | править вики-текст]
Выполнив тривиальную математическую операцию в выражении третьего закона Ньютона (5) и перенеся член из правой части в левую, получаем безупречную математически запись:
(6)
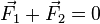
С физической точки зрения, сложение векторов сил имеет своим результатом получение равнодействующей силы.
В таком случае, прочтённое с точки зрения второго закона Ньютона выражение (6) означает, с одной стороны, что равнодействующая сил равна нулю и, следовательно, система из этих двух тел не двигается ускоренно. С другой стороны, здесь не высказаны никакие запреты на ускоренное движение самих тел.
Дело в том, что понятие о равнодействующей возникает лишь в случае оценки совместного действия нескольких сил на одно и то же тело. В данном же случае, хотя силы равны по модулю и противоположны по направлению, но приложены к разным телам и потому, касательно каждого из рассматриваемых тел по отдельности, не уравновешивают друг друга, поскольку на каждое из взаимодействующих тел действует лишь одна из них. Равенство (6) не указывает на взаимную нейтрализацию их действия для каждого из тел, оно говорит о системе в целом. [26][27]
Рис.1 Материальная точка в двух декартовых системах координат: неподвижной O, считающейся инерциальной, и подвижной O’
Повсеместно используется запись уравнения, выражающего второй закон Ньютона в инерциальной системе отсчёта:
(7)
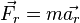
Если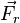 
есть результирующая всех реальных сил, действующих на тело, то это выражение, представляющее собой каноническую запись Второго закона, является просто утверждением, что получаемое телом ускорение пропорционально этой силе и массе тела. Оба выражения, стоящие в каждой части этого равенства, относятся к одному и тому же телу.
Но выражение (7) может быть, подобно (6), переписано в виде:
(8)
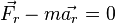
Для постороннего наблюдателя, находящегося в инерциальной системе и анализирующего ускорение тела, на основании сказанного выше такая запись имеет физический смысл только в том случае, если члены в левой части равенства относятся к силам, возникающим одновременно, но относящимся к разным телам. И в (8) второй член слева представляет собой такую же по величине силу, но направленную в противоположную сторону и приложенную к другому телу, а именно силу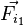 
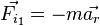
, то есть
(9)
В случае, когда оказывается целесообразным разделение взаимодействующих тел на ускоряемое и ускоряющее и, чтобы отличить действующие тогда на основании Третьего закона силы, те из них, которые действуют со стороны ускоряемого тела на ускоряющее, называют силами инерции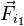 
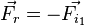
или «ньютоновыми силами инерции» [26] , что соответствует записи выражения (5) для Третьего закона в новых обозначениях:
(10)
Существенно, что сила действия ускоряющего тела на ускоряемое и сила инерции имеют одно и то же происхождение и, если массы взаимодействующих тел близки друг другу настолько, что и получаемые ими ускорения сравнимы по величине, то введение особого наименования «сила инерции» является лишь следствием достигнутой договорённости. Оно так же условно, как и само деление сил на действие и противодействие.
Иначе обстоит дело, когда массы взаимодействующих тел несравнимы между собой (человек и твёрдый пол, отталкиваясь от которого, он идёт). В этом случае деление тел на ускоряющие и ускоряемые становится вполне отчётливым, а ускоряющее тело может рассматриваться как механическая связь, ускоряющая тело, но не ускоряемая сама по себе
Центробе́жная си́ла [1] — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил.
Зачастую это бывает удобно. Например, когда вращается целиком вся лаборатория, может быть более удобным рассматривать все движения относительно нее, введя лишь дополнительно силы инерции, в том числе центробежную, действующие на все материальные точки, чем учитывать постоянное изменение положения каждой точки относительно инерциальной системы отсчета.
Часто, особенно в технической литературе, во вращающуюся с телом неинерциальную систему отсчёта переходят неявно, и говорят о проявлениях закона инерции как о центробежной силе, действующей со стороны движущегося по круговой траектории тела на вызывающие это вращение связи, и считают её по определению равной по модулю центростремительной силе и всегда направленной в противоположную ей сторону.
Однако в общем случае, когда мгновенный центр поворота тела по дуге окружности, которой аппроксимируется траектория в каждой её точке, может не совпадать с началом вектора силы, вызывающей движение, неверно называть действующую на связь силу силой центробежной. Ведь есть ещё составляющая силы связи, направленная по касательной к траектории, и эта составляющая будет изменять скорость движения тела по ней. Поэтому некоторые физики вообще избегают использовать термин «центробежная сила», как ненужный
Формулы[править | править вики-текст]
Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение этого понятия и может быть в некоторых случаях достаточно легко получено для релятивистской механики).
По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета.
Для материальной точки центробежная сила выражается формулой:
— центробежная сила приложенная к телу,
— масса тела,
— угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),
— радиус-вектор тела во вращающейся системе координат.
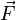
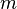
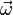
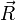
Эквивалентное выражение для центробежной силы можно записать как
если использовать обозначение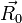 
для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.
Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело.
Вывод[править | править вики-текст]
Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью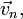 
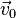
а сама система движется поступательно с линейной скоростью 
в инерциальной системе координат и одновременно вращается с угловой скоростью 
Тогда линейная скорость тела в инерциальной системе координат равна:
где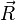 
— радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:
Найдём значение каждого слагаемого в инерциальной системе координат:
где 
— линейное ускорение относительно системы, 
— угловое ускорение.
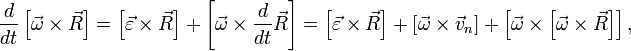
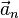
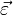
Таким образом, получаем:
Последнее слагаемое и будет центростремительным ускорением.
Раскрыв двойное векторное произведение и положив 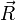перпендикулярным оси вращения, получим:
Элементарное рассмотрение и мотивировка[править | править вики-текст]
Ю. Г. Павленко
Лекции по теоретической механике
М.: ФИЗМАТЛИТ, 2002, 392 с.
ГЛАВА 1. УРАВНЕНИЯ НЬЮТОНА И ЛАГРАНЖА
Многообразие. Координаты. Евклидово пространство. Векторы в евклидовом пространстве. Скалярное произведение векторов. Векторное произведение векторов. Скалярное и векторное поля на многообразии. Тензоры в евклидовом пространстве. Диагонализация матрицы Производная определителя.
Система отсчета. Галилеево пространство. Кинематика. Базисные векторы. Угловая скорость одного базиса относительно другого. Два вращающихся базиса. Частица в пространстве. Скорость и ускорение в декартовых координатах. Скорость и ускорение в цилиндрических координатах. Естественные координаты.
Инерциальные системы отсчета. Силы в механике. Второй закон Ньютона. Третий закон Ньютона. Принцип относительности Галилея. Приближение внешнего поля.
Закон изменения импульса системы. Закон изменения момента импульса системы. Закон изменения кинетической энергии. Потенциальная энергия взаимодействия частиц Закон сохранения полной энергии. Уравнение Мещерского. Теорема вириала.
Одномерное движение в консервативном поле. Движение заряда в электромагнитном поле. Движение частицы в центрально-симметричном поле.
Потенциальная энергия взаимодействия однородного шара и частицы. Первые интегралы. Решение задачи Кеплера. Движение по эллипсу. Траектория частицы в пространстве. Орбитальные полеты. Коррекция траектории.
Лагранжиан, функционал действия. Принцип Гамильтона-Остроградского (или принцип наименьшего действия) Первые интегралы. Теорема Нетер. Движение системы во внешнем поле. Лагранжиан заряженной частицы в заданном электромагнитном поле. Вектор-потенциал магнитного поля соленоида.
Лагранжиан частицы в поступательно движущейся системе отсчета и во вращающейся системе отсчета.
ГЛАВА 2. ДВИЖЕНИЕ СИСТЕМЫ ЧАСТИЦ
Лагранжиан системы N частиц. Лагранжевы движения. Уравнения движения в относительных координатах. Задача трех тел. Переменные Якоби.
Лагранжиан и уравнения движения. Движение в системе центра масс (СЦМ). Приближение внешнего поля. Система Земля-Луна в поле тяготения Солнца. Гравитационная рогатка. Движение двух зарядов во внешнем поле.
Кинематика упругого рассеяния. Динамическая теория рассеяния. Сечение рассеяния реакции p1 + p2 → p’1 + p’2. Упругое рассеяние. Дифференциальные распределения в лабораторной системе. Обратная задача рассеяния. Условие классичности рассеяния. Рассеяние тождественных частиц.
Лагранжиан ограниченной задачи трех тел. Ограниченная круговая задача трех тел. Точки либрации. Вклад Луны в ускорение свободного падения.
Солнечная система. Наша Галактика и Вселенная. Полеты к Луне. Полеты к Венере. Полеты к Марсу. Космический вояж к дальним планетам. Сфера действия. Вторая космическая скорость. Третья космическая скорость. Четвёртая космическая скорость. Гомановская траектория перелета. Движение аппарата внутри сферы действия планеты-цели.
ГЛАВА 3. УРАВНЕНИЯ ЛАГРАНЖА СИСТЕМ СО СВЯЗЯМИ
Голономные связи. Силы реакции. Виртуальные перемещения. Идеальные связи. Метод неопределенных множителей Лагранжа. Закон изменения полной энергии. Принцип Д’Аламбера-Лагранжа. Неголономные связи.
Обобщенные координаты. Уравнения Лагранжа второго рода. Обобщенные импульс и энергия. Принцип Гамильтона. Движение в неинерциальной системе отсчета.
Координаты на поверхности. Векторные и тензорные поля на многообразии. Метрика на поверхности. Поднятие и опускание индексов. Геодезические кривые. Локально-геодезическая система координат. Ковариантное дифференцирование. Тензор кривизны. Тензор внешней кривизны. Расхождение геодезических.
ГЛАВА 4. ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
Одномерные колебания. Осциллятор в среде с линейным трением. Фазовый портрет линейного осциллятора. Система с s степенями свободы. Линейные колебания консервативной системы. Условия существования ограниченных решений. Биения. Нормальные координаты.
Одномерные колебания. Запаздывающая функция Грина. Энергия, потребляемая системой. Резонанс. Переходный и установившийся режимы. Колебания связанных систем.
Нелинейные системы. Нелинейные системы на плоскости. Синэргетика. Устойчивость по Ляпунову. Функция Ляпунова. Устойчивость по линейному приближению. Предельный цикл. Бифуркация. Бифуркация Хопфа. Бифуркация удвоения периода. Переход к хаосу. Детерминированный хаос. Система Лоренца. Странный аттрактор. Размерность Хаусдорфа. Фракталы. Хаос в динамических системах.
Решение нелинейных уравнений методом усреднения. Автоколебания. Вынужденная синхронизация. Система с медленно изменяющимися параметрами. Адиабатические инварианты. Параметрический резонанс в нелинейной системе. Многомерные системы.
ГЛАВА 5. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Координаты твердого тела. Углы Эйлера. Угловая скорость. Скорость и ускорение частиц твердого тела. Мгновенная ось вращения. Чистое качение. Динамические переменные. Тензор инерции. Твердое тело с одной неподвижной точкой.
Равновесие твердого тела. Уравнения Эйлера. Движение твердого тела с одной закрепленной точкой. Движение тела с неподвижной осью. Оси Резаля. Гироскопический момент.
Движение свободного твердого тела. Обобщенные импульсы и силы. Движение твердого тела с одной неподвижной точкой в однородном поле тяжести (случай Лагранжа). Плоскопараллельное качение твердого тела. Движение твердого тела относительно неинерциальной системы отсчета, вращающейся с угловой скоростью Ω(t). Космический аппарат (КА) в ньютоновом поле тяготения. Движение КА относительно центра масс. Гравилет.
Квазистационарные поля и токи. Функция Лагранжа электромеханической системы линейных проводников. Уравнения Лагранжа. Сила Ампера и момент силы Ампера. Магнитный момент проводника с током. Закон изменения обобщенной энергии. Нейтральная частица в электромагнитном поле. Твердое не ферромагнитное тело в магнитном поле.
ГЛАВА 6. КАНОНИЧЕСКИЕ УРАВНЕНИЯ
Преобразование Лежандра. Гамильтониан. Канонические уравнения. Функционал уравнений Гамильтона. Скобки Пуассона. Теорема Пуассона. Расширенное фазовое пространство. Интегрируемость гамильтоновых систем. Фазовый поток. Теорема Лиувилля.
Метод вариации канонических постоянных Производящие функции канониче¬ских преобразований Линейные канонические преобразования. Диагонализация гамильтониана. Операторная форма канонических преобразований. Канонические преобразования в классической теории магнитного резонанса.
Полный интеграл. Теорема Якоби. Метод разделения переменных. Перемен¬ные действие-угол. Метод характеристик. Метод Фока. Задача Коши. Классическая механика и квантовая механика. Уравнение Гамильтона—Якоби вр- представлении. Элементы гамильтоновой оптики.
Построение формальных рядов. Структура ряда теории возмущений. Условия существования решения. Интегрирование уравнений движения. Реакция системы на внешнее возмущение. Спонтанное и индуцированное излучение классических систем.
Секулярные члены. Методы усреднения гамильтоновых систем. Каноническое преобразование к медленным переменным. Локализация энергии в нелинейной системе. Параметрический резонанс. Система в быстроосциллирующем поле. Заряженная частица в высокочастотном поле.
Гамильтониан нелинейной системы первого порядка. Обращение интегралов. Решение алгебраических и трансцендентных уравнений. Усреднение слабонелинейных систем. Линейные сингулярно-возмущенные уравнения. Система общего вида.
Гамильтонова форма линейного уравнения второго порядка. Преобразование аргумента. Нормализация гамильтониана. Преобразование Лиувилля-Трина. Преобразование Беклунда. Высшие ВКБ-приближения. Решение в окрестности обыкновенной точки. Решение в окрестности регулярной особой (или правильной) точки. Исследование асимптотических разложений.
ГЛАВА 7. РЕЛЯТИВИСТСКАЯ МЕХАНИКА
Пространство Минковского. Преобразование Лоренца. Четырехмерные скорость и импульс частицы. Масса системы невзаимодействующих частиц. Электромагнитное поле. Лагранжиан и уравнения движения. Заряд в плосковолновом поле. Уравнения Гамильтона. Канонические преобразования. Уравнение Гамильтона-Якоби. Ковариантная теория возмущений в классической электродинамике.
Неинерциальные системы отсчета. Неинерциальные системы отсчёта. Силы инерции при ускоренном поступательном движении системы отсчета
| Название | Силы инерции при ускоренном поступательном движении системы отсчета |
| Анкор | Неинерциальные системы отсчета |
| Дата | 10.09.2021 |
| Размер | 57.79 Kb. |
| Формат файла |  |
| Имя файла | Неинерциальные системы отсчёта.docx |
| Тип | Закон #231233 |
 С этим файлом связано 1 файл(ов). Среди них: Закат как физическое явление.docx. Показать все связанные файлы Подборка по базе: Гигиена и силы природы.docx, Лабораторная работа №2 Измерение электродвижущей силы источника , Теория моментов инерции.doc, ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ОДНОРОДНОГО ДИСКА МЕТОДОМ КОЛЕБАНИЙ., 103. Определение момента инерции диска. Проверка теоремы Штейнер, Упраженения с отягощением направленные на развитие силы.docx,Неинерциальными называют такие системы отсчета, в которых не выполняются законы Ньютона. Не выполняется закон инерции, ибо в таких системах отсчета тело, на которое не действуют другие тела, не сохраняет своего состояния покоя или равномерного прямолинейного движения. Не выполняется второй закон Ньютона, так как тело может иметь ускорение, не испытывая действия со стороны другого тела. Наконец, не выполняется и третий закон Ньютона, ибо тело, испытывая действие некоторой силы инерции, не оказывает противодействия (нет тела, к которому должно быть приложено это противодействие). Различают два вида неинерциальных систем отсчета: системы, движущиеся относительно инерциальной системы отсчета поступательно с постоянным или переменным ускорением, и системы, вращающиеся с постоянной или переменной угловой скоростью относительно некоторого центра или некоторой оси. Произвольное движение системы всегда можно представить в виде суммы указанных двух движений. В НеИСО законы Ньютона в обычном виде применять нельзя, требуется введение специальных поправок — сил инерции. СИЛЫ ИНЕРЦИИ ПРИ УСКОРЕННОМ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ СИСТЕМЫ ОТСЧЕТА Пусть в равноускоренно движущемся вагоне нитью к потолку привязан шар. В инерциальной (лабораторной) системе отсчета второй закон Ньютона для груза имеет вид: Угол наклона нити легко можно найти, воспользовавшись «треугольником сил», откуда tgα=a/g . Для наблюдателя в вагоне шар покоится. Его ускорение равно нулю, хотя силы, действующие на шар, направлены не вдоль одной прямой и не могут компенсировать друг друга. Сохранить уравнение (1) и в левой части закона Ньютона получить ноль можно, если перенести слагаемое В правой части появилось новое слагаемое Иными словами, чтобы с точки зрения наблюдателя, находящегося в НеИСО, объяснить покой тела, мы вынуждены ввести новую силу Важно, что в силе инерции m – масса тела, к которому сила приложена, Проявление сил инерции при поступательном движении мы можем видеть в повседневных явлениях. Если поезд набирает скорость, то пассажир, сидящий при этом по ходу поезда, прижимается к спинке сиденья под действием силы инерции. Наоборот, при торможении поезда пассажир отклоняется от спинки сиденья, т. к. сила инерции направлена в противоположную сторону. Особенно силы инерции заметны при внезапном торможении поезда. Эти силы проявляются в перегрузках, возникающих при запуске и торможении космических кораблей. Пусть диск равномерно вращается с угловой скоростью ω (ω=const) вокруг перпендикулярной ему оси, которая проходит через его центр. На диске установлены маятники, на разных расстояниях от оси вращения и на нитях висят шарики массой m, изображенной на рис.1 . Когда диск начнет вращаться, шарики отклоняются от вертикали на некоторый угол. В инерциальной системе отсчета, которая связана, например, с помещением, где установлен диск, происходит равномерное вращение шарика по окружности радиусом R (расстояние от центра масс вращающегося тела до оси вращения), рис.2 Второй закон Ньютона имеет вид: Угол отклонения нити снова можно найти из «треугольника сил»: Относительно системы отсчета, которая связана с вращающимся диском, шарик покоится, что возможно, если силы Сила На практике действие центробежных сил инерции испытывают, например, пассажиры в движущемся автобусе на поворотах, летчики при выполнении фигур высшего пилотажа, дети на карусели; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах, в режиме отжима в стиральных машинах и т. д., где они достигают очень больших значений. При проектировании быстро вращающихся деталей машин (винтов самолетов, роторов и т. д.) используются специальные механизмы для уравновешивания центробежных сил инерции. Из формулы (5) следует, что центробежная сила инерции, которая действует на тела во вращающихся системах отсчета и которая направлена в сторону радиуса от оси вращения, зависит от угловой скорости вращения ω системы отсчета и радиуса R , но при этом не зависит от скорости тела относительно вращающихся систем отсчета. Значит, центробежная сила инерции действует во вращающихся системах отсчета на все тела, которые удалены от оси вращения на конечное расстояние, при этом не имеет значения, покоятся ли они в этой системе отсчета (как мы предполагали до сих пор) или движутся относительно нее с некоторой скоростью. Но еще раз оговоримся, что реально центробежных сил нет! Это лишь плата за выбор системы отсчета, в которой для объяснения стремления тела двигаться прямолинейно (по инерции) приходится вводить фиктивную силу. Cила Кориолиса действует только на тела, которые движутся относительно вращающейся системы отсчета, чаще всего рассматривается случай относительно Земли. Действием этих сил объясняется ряд наблюдаемых на Земле явлений. Так, на тело, движущееся в северном полушарии на север, действует сила Кориолиса, направленная вправо по отношению к направлению движения, т. е. на восток. Если тело движется на юг, то сила Кориолиса также действует вправо, если смотреть по направлению движения, т. е. тело отклоняется на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, и т. д. В южном полушарии все наоборот. Благодаря действию силы Кориолиса падающие на поверхность Земли предметы отклоняются к востоку. С силой Кориолиса связано движение маятника Фуко, которое явилось в свое время одним из доказательств вращения Земли. Если бы силы Кориолиса не было, то плоскость колебаний качающегося вблизи поверхности Земли маятника оставалась бы неизменной (относительно Земли). Действие же данной силы приводит к вращению плоскости колебаний вокруг вертикального направления. https://foxford.ru/wiki/fizika/neinertsialnye-sistemy-otschyota
источники: http://alexandr4784.narod.ru/pavlenkotm.html http://topuch.ru/sili-inercii-pri-uskorennom-postupatelenom-dvijenii-sistemi-ot/index.html |
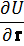
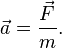
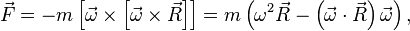
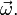
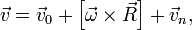
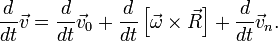
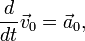
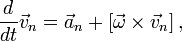
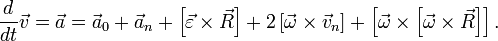
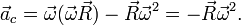
(1)
в правую часть. Тогда получим
(2)
. Так как оно находится в «области сил», то и название у него — сила инерции.
. (3). По сути, этой силы НЕТ! Она не имеет природы, и у нее нет пары по третьему закону Ньютона. Приложена сила инерции к центру масс тела, направлена против ускорения НеИСО. Для любого из тел, которые находятся в неинерциальной системе отсчета, силы инерции являются внешними; следовательно, нет замкнутых НеИСО, т. е. в неинерциальных системах отсчета не выполняются также и законы сохранения импульса, энергии и момента импульса, аккуратно надо применять законы статики.
− ускорение не тела а самой НеИСО, в которую мы пересели!
, (4) где 
− нормальное или центростремительное ускорение.
, т. е. углы отклонения нитей маятников будут тем больше, чем больше угловая скорость вращения ω и чем больше расстояние R от центра шарика до оси вращения диска.
и 
уравновешиваются силой 
, являющейся не чем иным, как силой инерции, так как никакие другие силы на шарик не действуют.
(5).
(6)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
