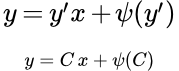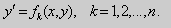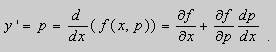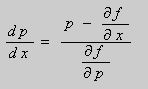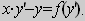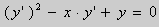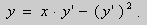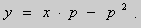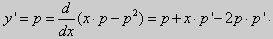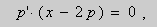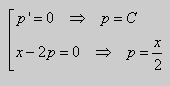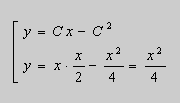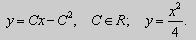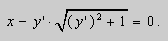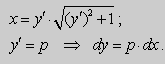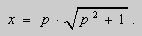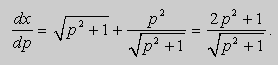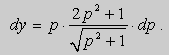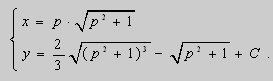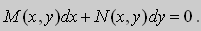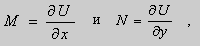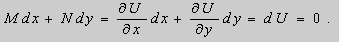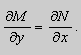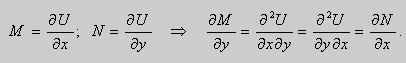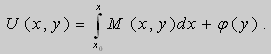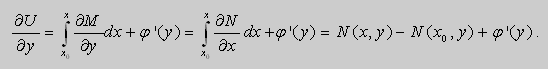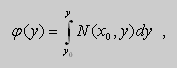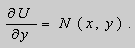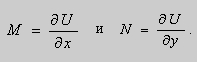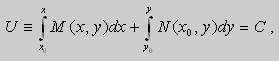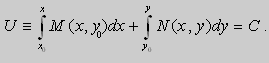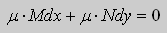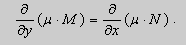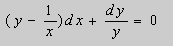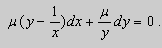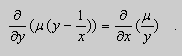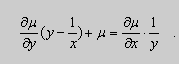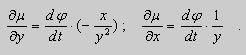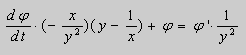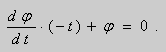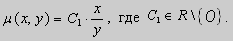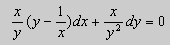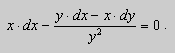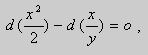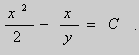Уравнения лагранже и клеро задачи

Дифференциальное уравнение Клеро

Решение дифференциального уравнения Клеро

Рассмотрим уравнение Клеро:
(1)
Не трудно убедиться, что его общее решение имеет вид:
(2)

Действительно, поскольку – постоянная, то – тоже постоянная. Тогда дифференцируя (2) имеем:
;
(3) .
Подставляя (2) и (3) в (1), получаем тождество:
.

Особое решение дифференциального уравнения Клеро

Уравнение Клеро может иметь особое решение. Как известно, если общее решение дифференциального уравнения имеет вид:
,
то особое решение может получиться исключением из уравнений:
;
.

В нашем случае, решение (2) можно записать в виде:
.
Тогда
.
Тогда особое решение может получиться, исключением из уравнений:
;
.

Поскольку возможны посторонние решения, то после нахождения особого решения, необходимо проверить, удовлетворяет ли он исходному уравнению (1).

Пример

Решить уравнение:
(1.1)

Это уравнение Клеро. Его общее решение имеет вид:

Ищем особое решение. Перепишем общее решение в виде:
.
Дифференцируем по :

.
Тогда особое решение может получиться исключением из уравнений:
(1.2) ;
(1.3) .

Исключаем . Из уравнения (1.3) имеем:
(1.4) .
Возводим в квадрат и преобразуем:
;
;
. Отсюда следует, что .
Извлекаем квадратный корень:
(1.5) .
Поскольку мы возводили в квадрат, то, возможно, (1.5) содержит лишние решения, которые не удовлетворяют (1.4). Сейчас мы примем (1.5), а отсев лишних решений сделаем в самом конце.
Подставим (1.4) и (1.5) в (1.2):
.

Итак, особые решения имеют вид:
(1.6) .
Теперь сделаем проверку, чтобы выяснить, удовлетворяет ли исходному уравнению (1.1):
(1.1) .
Находим производную (1.6) и выполняем преобразования:

;
;
.
Подставляем в (1.1):
(1.7) .

При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять нижний знак:
.
То есть при , .

При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять верхний знак:
.
То есть при , .

Общее решение уравнения имеет вид:

При уравнение имеет особое решение:
.

При уравнение имеет особое решение:
.

Автор: Олег Одинцов . Опубликовано: 24-08-2012 Изменено: 10-04-2016

Лекция 2. Дифференциальные уравнения первого порядка, не разрешённые относительно производной .

Рассмотрим уравнение вида

F ( x , y , y ‘ ) = 0 ,

не разрешённое относительно производной. Если попытаться выразить из него y ‘ , то можно получить , вообще говоря , несколько уравнений

Геометрически это означает , что в каждой точке задаётся несколько направлений поля (см.рис.2).

Следовательно через любую точку M ( x , y ) может проходить несколько интегральных кривых . Для того, чтобы выделить из этого множества единственную интегральную кривую, проходящую через заданную точку M₀ ( x₀ , y₀) , надо помимо значений ( x₀ , y₀ ) дополнительно задать в этой точке направление поля y ‘ ( x₀) = y ‘_{0 .}

Задача Коши . Найти решение 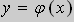уравнения F ( x , y , y ‘ ) = 0, удовлетворяющее начальным условиям y ( x₀) = y₀ и y ‘ ( x₀) = y ‘₀ , где y ‘₀ — решение уравнения F ( x₀ , y₀ , y ‘ ) = 0.

Теорема существования и единственности решения задачи Коши.

Пусть в некоторой окрестности U точки (x₀ , y₀ , y ‘₀ ), где y ‘₀ — решение уравнения F ( x₀ , y₀ , y ‘ ) = 0, выполнены условия :

1) F( x , y , y ‘ ) определена, непрерывна и имеет непрерывные частные производные F’_y и F’_{y ‘} по совокупности переменных ( x , y , y ‘ ) ;

2) значение производной F_y‘_‘ (x₀ , y₀ , y’₀ )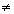0.

Тогда в некоторой окрестности точки x₀ существует единственное решение 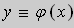уравнения F (x, y, y’) = 0, удовлетворяющее условиям y(x₀) = y₀ и y’ (x₀) = y’₀ .

Метод введения параметра.

На практике при решении уравнений F( x , y , y ‘ ) = 0 часто используют следующий метод.

Предположим , что уравнение F( x , y , y ‘ ) = 0 “легко” решить относительно y : y = f ( x , y ‘ ). Тогда введем замену y ‘ = p ( параметр зависит от x ). Предполагая, что дифференциальное уравнение имеет решение y = y ( x ) , получим ( в силу уравнения )

Из этих равенств выражаем :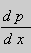

Это уравнение разрешено относительно производной 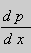. Пусть его общее решение имеет вид p = p ( x , C ) .Тогда общее решение заданного уравнения можно записать в виде y =f ( x , p ( x , C ) ). Решение найдено.

Таким методом можно решать , в частности , уравнения Лагранжа и Клеро.

Уравнение вида 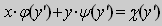называется уравнением Лагранжа. Оно является линейным относительно переменных x и y . Частным случаем этого уравнения является уравнение Клеро. Оно имеет вид :

Пример 1 . Решить уравнение

Решение. Выразим из уравнения (5) переменную y :

.Заменим 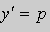и получим

Продифференцируем его по x :

Из этих равенств получаем :

После подстановки этих выражений в (6) будем иметь

Ответ :

Этим методом можно также решать уравнения , в которых «легко» выражается переменная x . Рассмотрим

Пример 2 . Решить уравнение

Решение . Выразим из уравнения (7) переменную x и введём параметр p :

Продифференцируем уравнение (8) по p :

Отсюда в силу равенства dy = p dx получим :

Проинтегрируем это уравнение :

Таким образом , с учётом ( 8 ) , получаем общее решение в параметрическом виде :

Примеры. Решить уравнения :

Уравнения в полных дифференциалах.

Если в уравнении (9) функции

В этом случае уравнение (9) называют уравнением в полных дифференциалах. После интегрирования получим общее решение уравнения

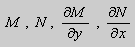
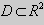
Теорема 1. Пусть функции непрерывные в некоторой односвязной области . Тогда необходимым и достаточным условием того, что уравнение (9) — в полных дифференциалах , является условие

Доказательство. 1. Необходимость.

Если выбрать функцию 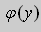та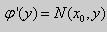к, чтобы

то и , следовательно ,

Таким образом , в уравнении (9)

Теорема 1 доказана.

Из теоремы следует , что общее решение уравнения (9) можно записать в виде

если 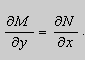Функцию U можно также представить в виде

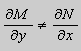
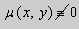
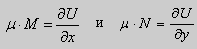
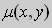
Предположим , что . Тогда можно попытаться найти такую функцию , чтобы . Функция называется интегрирующим множителем . В этом случае мы получаем уравнение

в полных дифференциалах. Следовательно, в силу теоремы 1,

Это уравнение позволяет найти интегрирующий множитель. Рассмотрим

Пример. Решить уравнение

Решение. Простой проверкой убеждаемся , что (10) не является уравнением в полных дифференциалах. Умножим его на неизвестную функцию :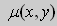

Попробуем найти 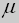из уравнения :

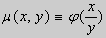
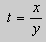
Пусть . Обозначим через и получим

После подстановки этих выражений в (11) будем иметь :

Проинтегрируем полученное уравнение :

Таким образом, интегрирующий множитель можно взять в виде

Умножим теперь уравнение (10) на функцию

Теорема 2. Если функции M и N непрерывные , имеют непрерывные частные производные первого порядка по x и по y , и 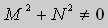, то интегрирующий множитель существует.

Замечание. Точка ( x₀ , y₀ ), в которой M ( x₀ , y₀ ) = N ( x₀ , y₀ ) = 0 является особой точкой уравнения (9). Поведение решений в окрестности особой точки изучается в лекции 3.

Примеры. Решить дифференциальные уравнения :

Уравнение Клеро

Вы будете перенаправлены на Автор24

Дифференциальные уравнения первого порядка, не разрешенные относительно производной.

В общем виде дифференциальные уравнения первого порядка, не разрешенные относительно производной, записываются как $F\left(x,y,y’\right)=0$.

Основной метод решения таких дифференциальных уравнений состоит в том, чтобы выполнить некоторые преобразования, приводящие к уравнениям, разрешенным относительно производной. В дальнейшем могут применяться любые из известных методов, соответствующие тому, что в результате получилось: или уравнение с разделяющимися переменными, или однородное уравнение, или линейное уравнение и т.п.

Решить дифференциальное уравнение $y’^ <3>-y’^ <2>\cdot x+2\cdot y’=2\cdot x$.

Данное дифференциальное уравнение не разрешено относительно производной, поэтому известные методы для его решения применить не удается.

Поэтому выполняем следующие преобразования:

• все слагаемые переносим в одну сторону $y’^ <3>-y’^ <2>\cdot x+2\cdot y’-2\cdot x=0$;
• выражение слева разлагаем на множители $\left(y’^ <2>+2\right)\cdot \left(y’-x\right)=0$;
• так как $y’^ <2>+2\ne 0$, то исходное уравнение эквивалентно $y’-x=0$.

Получено дифференциальное уравнение, допускающее непосредственное интегрирование: $\frac =x$.

Отсюда: $y=\int x\cdot dx $; $y=\frac > <2>+C$.

Решить дифференциальное уравнение

\[y’^ <2>-y’\cdot y+\cos x\cdot \left(y’-y\right)=0.\]

Данное дифференциальное уравнение не разрешено относительно производной, поэтому выполняем преобразования:

\[y’\cdot \left(y’-y\right)+\cos x\cdot \left(y’-y\right)=0;\] \[\left(y’-y\right)\cdot \left(y’+\cos x\right)=0.\]

Таким образом, данное дифференциальное уравнение эквивалентно двум другим: $y’-y=0$ и $y’+\cos x=0$.

Первое дифференциальное уравнение $y’-y=0$ решается посредством разделения переменных:

Второе дифференциальное уравнение $y’+\cos x=0$ допускает непосредственное интегрирование: $\frac =-\cos x$, откуда $y=-\sin x+C$.

Метод введения параметра

В ряде случаев дифференциальное уравнение вида $F\left(x,y,y’\right)=0$ не удается разрешить относительно производной. Но вполне возможно, что оно разрешимо или относительно $y$, или относительно $x$. Тогда мы получаем дифференциальное уравнение общего вида $y=u\left(x,y’\right)$ или $x=v\left(y,y’\right)$. Некоторые из дифференциальных уравнений подобного вида можно решить методом введения параметра.

Рассмотрим пример дифференциального уравнения вида $x=f\left(y’\right)$.

Решается введением параметра $\frac =p$.

В результате имеем решение данного дифференциального уравнения в параметрической форме, задаваемое следующими выражениями:

Готовые работы на аналогичную тему

Решить дифференциальное уравнение $8\cdot y’^ <3>=27\cdot x$.

Здесь мы имеем дифференциальное уравнение вида $x=f\left(y’\right)$, не разрешенное относительно производной.

Вводим параметр $\frac =p$ и записываем уравнение в виде $x=\frac<8> <27>\cdot p^ <3>$.

Здесь $f\left(p\right)=\frac<8> <27>\cdot p^ <3>$, откуда $\frac =\frac<8> <27>\cdot 3\cdot p^ <2>=\frac<8> <9>\cdot p^ <2>$.

Таким образом, решение данного дифференциального уравнения в параметрической форме задается следующими выражениями:

Отсюда получаем: $\left\<\begin <27>\cdot p^ <3>> \\ <9>\cdot \frac<1> <4>\cdot p^ <4>+C> \end\right. $ или $\left\<\begin <27>\cdot p^ <3>> \\ <9>\cdot p^ <4>+C> \end\right. $ — решение данного дифференциального уравнения в параметрической форме.

Параметр $p$ из этой системы уравнений можно исключить:

из $x=\frac<8> <27>\cdot p^ <3>$ получаем $p^ <3>=\frac<27> <8>\cdot x$ или $p=\frac<3> <2>\cdot x^<\frac<1> <3>> $;

подставляем в $y=\frac<2> <9>\cdot p^ <4>+C$ и получаем $y=\frac<2> <9>\cdot \left(\frac<3> <2>\cdot x^<\frac<1> <3>> \right)^ <4>+C$ или $y=\frac<9> <8>\cdot x^<\frac<4> <3>> +C$.

Таким образом, получено общее решение $y=\frac<9> <8>\cdot x^<\frac<4> <3>> +C$ данного дифференциального уравнения $8\cdot y’^ <3>=27\cdot x$ в явной форме.

Решение уравнения Клеро

Уравнение Клеро имеет вид $y=x\cdot y’+\psi \left(y’\right)$ и относится к более сложным видам дифференциальных уранений, не разрешенных относительно производной.

Введим параметр $\frac =p$, в результате чего имеем $y=x\cdot p+\psi \left(p\right)$.

После дифференцирования и простых преобразований получаем уравнение $\frac \cdot \left(x+\psi ‘\left(p\right)\right)=0$, которое распадается на два дифференциальных уравнения $\frac =0$ и $x+\psi ‘\left(p\right)=0$.

Из этого уравнения следует $p=C$. Отсюда получаем общее решение дифференциального уравнения Клеро $y=x\cdot C+\psi \left(C\right)$. Иначе говоря, общее решение можно получить из данного уравнения $y=x\cdot y’+\psi \left(y’\right)$ формальной заменой $y’$ на $C$.

Уравнение $x+\psi ‘\left(p\right)=0$.

Это уравнение дает особое решение в параметрической форме:

Оно представляет собой огибающую семейства кривых общего решения.

Решить дифференциальное уравнение $y=x\cdot y’+y’$.

Имеем уравнение Клеро, в котором $\psi \left(y’\right)=y’$.

Вводим параметр $\frac =p$ и получаем $y=x\cdot p+p$, где $\psi \left(p\right)=p$.

Формально заменив в данном дифференциальном уравнении $y’$ на $C$, получим его общее решение $y=x\cdot C+C$ или $y=C\cdot \left(x+1\right)$.

Находим особое решение.

Так как $\psi \left(p\right)=p$ и $\frac =1$, то особое решение в параметрической форме преобразуется к виду: $\left\<\begin \\ \end\right. $. Это значит, что особые решения для данного дифференциального уравнения отсутствуют.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 19 01 2022