Уравнения лапласа для электрического поля в проводящей среде

Электрическое поле в проводящей среде подчиняется уравнению Лапласа

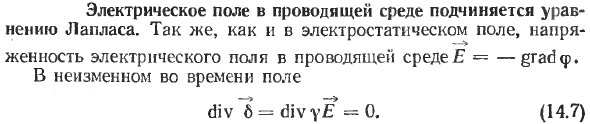
Электрическое поле в проводящей среде подчиняется уравнению Лапласа

Электрическое поле проводящей среды следует уравнению Лапласа. Подобно электростатическому полю, напряженность электрического поля проводящих сред составляет E = —град

• Для полей, не зависящих от времени, div 6 = divy £ = 0- (14.7) Если среда не меняется от точки к точке, то есть если среда однородна и изотропна,

то y как постоянное значение можно взять из знака расходимости Людмила Фирмаль

Вместо divуЕ-0 вы можете написать div divЕ = 0 или divÅ = 0. (14.8) Другими словами, div (-gradtp) = О или V?

Следовательно, оно следует полевому уравнению Лапласа для однородной проводящей среды.

• Уравнение Лапласа описывает потенциальное поле.

Следовательно, поле постоянного тока в проводящей среде

является потенциальным полем. Людмила Фирмаль

Среди них в районах, не занятых источниками (г-н Эдл-0.

Если вам потребуется заказать решение по электротехнике (ТОЭ) вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

2.4. Уравнение Лапласа для электрического поля в проводящей среде

Поскольку электрическое поле в проводящей среде является потенциальным, то справедливо равенство

.

Подставив последнее выражение в уравнение для плотности тока (2.1), а затем плотность тока в уравнение (2.3), получим

Если среда однородна и изотропна по отношению к удельной проводимости, то

Таким образом, поле в однородной проводящей среде подчиняется уравнению Лапласа.

Три группы формул Максвелла

13.2.11. Три группы формул Максвелла

В системе нескольких заряженных тел потенциал каждого из них определяется не только зарядом данного тела, но и зарядами всех остальных тел. При этом, если диэлектрическая проницаемость среды не зависит от напряженности электрического поля, то потенциал оказывается линейной функцией зарядов.

В матричной форме система уравнений с потенциальными коэффициентами для n заряженных тел имеет вид: j = aq. (13.37а)

Здесь j и q – матрицы-столбцы, a – квадратная матрица. Каждая матрица имеет n строк.

Эта система и представляет собой первую группу формул Максвелла для электростатики. Она позволяет вычислить потенциалы тел по заданным зарядам.

В частности, для тела с номером k можно записать

(13.37б)

и сами коэффициенты определить с помощью эксперимента (или рассчитать) при следующих условиях.

Если все заряды, кроме , положить равными нулю, то собственный потенциальный коэффициент, как следует из (13.37б), будет равен . В свою очередь, взаимный потенциальный коэффициент можно найти через потенциал того же тела, но при равенстве нулю всех зарядов, кроме : .

Вторую группу формул Максвелла – уравнения с емкостными коэффициентами (коэффициентами электростатической индукции)– нетрудно получить, разрешив систему уравнений (13.37а) относительно зарядов тел. В матричной форме:

Эта группа позволяет вычислить заряды тел по заданным потенциалам.

Из уравнения для k-го тела

. (13.38б)

следует способ определения коэффициентов. Если принять равными нулю потенциалы всех тел, кроме , то собственный емкостный коэффициент равен . Взаимный емкостный коэффициент выражается через заряд того же тела и не равный нулю потенциал тела с номером m, причем потенциалы остальных тел равны нулю: . Очевидно, квадратные матрицы коэффициентов в уравнениях (13.37а) и (13.38а) взаимно обратны:

Третья группа формул Максвелла – уравнения с частичными емкостями – связывает заряды тел с разностями потенциалов между телами (в том числе и с землей, чей потенциал считается равным нулю). Эти уравнения можно получить из второй группы формул перегруппировкой слагаемых. Матричная запись системы уравнений имеет вид:

В уравнении для k-го тела

. (13.39б)

переменные равны: .

Для определения собственной частичной емкости следует принять потенциалы всех тел одинаковыми и определить заряд тела с номером k. Тогда . Если этот результат сравнить с записью в тех же условиях уравнения с емкостными коэффициентами, то легко убедиться, что

. (13.39в)

Чтобы найти взаимную частичную емкость, нужно принять потенциалы всех тел, кроме m — го, равными нулю, иными словами, заземлить и определить заряд k-го тела. Тогда . Очевидно, . При этом, поскольку на заземленном теле наводится заряд противоположного знака по сравнению с , который определяется потенциалом , то все частичные емкости и собственный емкостный коэффициент положительны, а взаимные емкостные коэффициенты отрицательны. Разумеется, положительны и все потенциальные коэффициенты. Кроме того, в соответствии с принципом взаимности

.

Пример 13.11. Двухпроводная линия над землей (рис. 13.11,а).

Известны расстояние между проводами d, высота подвеса над землей h, радиус и длина l каждого из них.

Определить потенциальные коэффициенты и емкость единицы длины линии с учетом влияния земли.

Длину проводов будем полагать достаточно большой, чтобы поле можно было считать плоскопараллельным. А радиус провода по сравнению с высотой подвеса и расстоянием между проводами достаточно малым, чтобы не учитывать смещения электрических осей проводов относительно геометрических.

Для определения потенциальных коэффициентов воспользуемся методом зеркальных изображений (рис. 13.11,б). Пусть известен заряд первого провода q, а заряд второго провода равен нулю. Тогда зеркальное изображение первого провода имеет заряд – q. Найдем потенциалы проводов, используя формулу (13.26), в которой заменим .

Очевидно, .

Отсюда легко находятся потенциальные коэффициенты:

.

Уравнения для двух заряженных проводов имеют вид:

.

Чтобы определить емкость линии с учетом влияния земли, следует принять (при этом, очевидно, и ). Тогда

.

Подставляя значения коэффициентов, найдем и емкость единицы длины линии .

Если высота подвеса гораздо больше расстояния между провода ми, то полученное выражение приводится к формуле (13.36).

13.3. Электрическое поле постоянных токов

в проводящей среде

13.3.1. Уравнение Лапласа

Постоянный ток в окружающей среде создает как электрическое, так и магнитное поле. Если рассматривать электрическую составляющую, то из полной системы уравнений электромагнитного поля в расчет следует взять только три. Тождество позволяет из уравнения (13.1б) получить принцип непрерывности электрического тока:

. (13.40)

Вне источников электрической энергии уравнение (13.2б) упрощается:

. (13.41)

Свойства проводящей среды в каждой точке учитываются законом Ома в дифференциальной форме:

. (13.42)

Уравнение (13.41) говорит о том, что, как и в электростатике, электрическое поле постоянного тока в проводящей среде – безвихревое, а значит, потенциальное. Поэтому и в данном случае справедлива формула (13.12):

Подстановка этого выражения в (13.42), а последнего в (13.40) приводит к уравнению Лапласа (13.15): Для того, чтобы решить это уравнение, нужно знать граничные условия, в первую очередь однородные – на поверхности раздела двух сред.

13.3.2. Граничные условия на поверхности раздела двух сред

с различными удельными проводимостями

Выделим точку на поверхности раздела двух проводников, через которую протекает ток, и рассмотрим электрическое поле вблизи нее. Как и в разделе 13.2.3, окружим эту точку некоторой замкнутой цилиндрической поверхностью. Причем будем считать, что высота цилиндра гораздо меньше диаметра оснований. На рис. 13.12,а контур abcda – это след цилиндрической поверхности в плоскости чертежа, которая проходит через ось цилиндра. Вычислим ток сквозь эту поверхность и воспользуемся принципом непрерывности (13.40). Учитывая соотношение размеров цилиндра, током сквозь боковую поверхность можно пренебречь, подсчитав лишь ток сквозь поверхности оснований и приравняв его нулю:

.

Поверхности оснований столь малы, что в их пределах векторы и не меняются. В результате интегрирования скалярных произведений векторов с учетом их расположения по отношению к нормали , получим: . Тогда

(13.43)

Итак, в точке, лежащей на поверхности раздела двух проводящих сред, нормальные составляющие вектора плотности электрического тока равны.

Теперь окружим ту же точку прямоугольным контуром abcda в плоскости чертежа (рис. 13.12,б) и подсчитаем циркуляцию вектора Е, сохранив соотношение ab = cd > bc = da. Напомним, что источники энергии не попадают в контур интегрирования, поэтому в соответствии с формулой (13.11а) получим. Если считать и отрезки ab и cd столь малыми, что в их пределах векторы и не меняются, то интегралы от скалярных произведений с учетом расположения векторов по отношению к нормали n1n2 перейдут в равенство: . Отсюда

(13.44)

В точке, лежащей на поверхности раздела двух проводящих сред, касательные составляющие вектора напряженности электрического поля равны. Это условие также означает, что при переходе через поверхность раздела двух диэлектриков потенциал изменяется плавно, без скачков.

Кроме того, из формул (13.42)–( 13.44) следует еще одно условие:

. (13.45)

13.3.3. Граничные условия на поверхности раздела

проводника и диэлектрика

Повторив рассуждения предыдущего раздела применительно к точке, лежащей на поверхности раздела проводника и диэлектрика (рис. 13.1,в), убедимся в том, что и здесь справедливо равенство касательных составляющих напряженности электрического поля (13.44).

При этом и вектор плотности тока на поверхности проводника имеет только касательную составляющую (постоянный ток в диэлектрике не течет), так что

(13.46)

Разумеется, в диэлектрике существует и нормальная составляющая напряженности электрического поля, причем, как правило, гораздо большей величины, чем нормальная. Но она не связана с протеканием тока внутри проводника.

13.3.4. Аналогия между электрическим полем тока

в проводящей среде и электростатическим полем в диэлектрике

Если сравнить выражения, описывающие эти два поля (табл. 13.4), то нетрудно заметить, что они отличаются лишь обозначениями. Это так называемая математическая аналогия.

Электрическое поле тока

(r = 0)

Аналогами являются потенциал j, напряжение U и вектор напряженности электрического поля Е в обеих средах (здесь и обозначения одинаковы). Вектор плотности электрического тока d, ток I и удельная проводимость g соответствуют вектору D, потоку вектора электрического смещения и абсолютной диэлектрической проницаемости . Если же подсчитать ток и поток сквозь замкнутую поверхность, то аналогами окажутся источник тока J и заряд q, а также коэффициенты пропорциональности – проводимость и емкость:

Отсюда (при одинаковой геометрии системы) следует соотношение

Существенно отличаются лишь граничные условия на поверхности раздела проводника и диэлектрика. Если в электростатике и то для поля тока и Это важно при использовании метода зеркальных изображений. Если в электростатике зеркальным изображениям тел придавались заряды те же по величине, что и у реальных тел, но противоположного знака, то зеркальные изображения проводящих тел должны иметь ток того же направления. Только в этом случае поле в однородной среде будет обладать такой симметрией, которая нужна для выполнения граничных условий реальной задачи.

На формальном соответствии уравнений, часть из которых приведена в табл. 13.4 основан так называемый метод электростатической аналогии. С одной стороны, этот метод позволяет использовать при расчете поля в проводящей среде готовые решения аналогичных задач электростатики. С другой, – можно заменить экспериментальное исследование электростатического поля (весьма сложное из-за искажений, вносимых зондом) экспериментами в проводящей среде, где подобные искажения несущественны. Рассмотрим обе возможности подробнее.

Пример 13.12. Поле металлического заземлителя в форме полушария, расположенного у поверхности земли (рис. 13.13,а).

Известны радиус м, ток J = 10 А, удельная проводимость грунта См/м.

Определить сопротивление заземления и шаговое напряжение.

Ток стекает через металлический электрод (заземлитель) в грунт, равномерно растекается в толще земли, чтобы собраться у другого заземлителя, включенного в цепь общего источника. Чтобы свести задачу к расчету поля в однородной среде воспользуемся методом зеркальных изображений. Очевидно, заданные условия полностью сохраняются в нижней полуплоскости системы, изображенной на рис. 13.13,б. Но в соответствии с методом электростатической аналогии решение этой новой задачи должно быть подобно расчету поля уединенного заряженного шара (рис. 13.2,б).

В частности, используя формулу емкости из примера 13.7 и соотношение (13.47), можно подсчитать проводимость шарового заземлителя:

.

Проводимость одного полушария, естественно, вдвое меньше. Поэтому сопротивление заземления равно

Ом.

Под шаговым напряжением понимается разность потенциалов между точками на поверхности земли, находящимися на расстоянии шага человека друг от друга. Обычно принимают это расстояние равным м. Очевидно, наибольшее значение напряжения получается между точками a и b на рис. 13.13,а. И здесь на помощь приходит формула (13.23), в которой следует заменить q на 2J и на g. Результат:

В.

Электростатическое поле удобно изучать на модели, выполненной в проводящей среде. Электромоделирование основано на очевидном факте. Если систему металлических электродов, имеющих разные потенциалы, залить раствором солей, проводимость которого на несколько порядков меньше проводимости самих электродов, то положение эквипотенциальных поверхностей не изменится.

Поэтому для моделирования электростатического поля обычно используются так называемые электролитические ванны. В такую ванну, выполненную из изолирующего материала и заполненную раствором (электролитом), помещаются металлические электроды, форма которых подобна форме заряженных тел в электростатическом поле

(рис. 13.14). Размеры модели выбираются такими, чтобы можно было пренебречь влиянием стенок ванны.

Потенциалы определяются с помощью зонда (З), который вместе с нуль-индикатором (НИ) включается в диагональ моста, плечами которого служат части реостата (Р) и участки электролита между электродами (А и Б). Во избежание электролиза измерения проводятся при синусоидальном напряжении источника низкой (50–400 Гц) частоты, а в качестве комбинации электрод – электролит используются медь – раствор медного купороса или нержавеющая сталь дистиллированная (или

очищенная водопроводная) вода. Возможно использование и твердых моделей. Это может быть либо специальная проводящая бумага, либо так называемая сеточная модель, в которой проводящая среда заменена набором сопротивлений.

13.4. магнитное поле постоянных токов

13.4.1. Скалярный и векторный магнитные потенциалы

Магнитное поле выявляется по силовому воздействию на неподвижные проводники с токами. Сила, действующая в магнитном поле с индукцией B на элемент dl проводника с током I, определяется законом Ампера: , причем направление вектора dl совпадает с направлением тока (рис. 13.15). Все три вектора в этом выражении взаимно перпендикулярны друг другу.

Уравнения магнитного поля постоянных токов в дифференциальной форме выведены в разделе 1б, 13.4б, 13.7):

, ,

Первое из этих уравнений говорит о том, что в областях, занятых током, магнитное поле имеет вихревой характер. А вне этих областей, где , магнитное поле безвихревое и, значит, потенциальное. Иными словами, вектор напряженности магнитного поля можно представить в виде

(13.48)

Тогда откуда следует уравнение Лапласа для скалярного магнитного потенциала jм:

(13.49)

Для областей, занятых током, это уравнение не годится. Там можно ввести новую функцию – векторный магнитный потенциал А, который связан с вектором магнитной индукции соотношением

В этом случае тождественно удовлетворяется принцип непрерывности магнитного потока: . Тогда

= d.

Если, не нарушая соотношения (13.50), в последнем выражении принять div A = 0, то из него следует уравнение Пуассона для векторного магнитного потенциала А:

(13.51а)

Естественно, в областях, незанятых током (d = 0), оно переходит в уравнение Лапласа

(13.51б)

Уравнения (13.51а) и (13.51б) – векторные. Каждое из них распадается на три скалярных, связывающих между собой проекции векторов А и d на оси декартовой системы координат:

Отметим, что с использованием векторного магнитного потенциала существенно упрощается вычисление магнитного потока. Действительно, . Теорема Стокса позволяет преобразовать поверхностный интеграл в контурный, который вычислять гораздо проще:

. (13.53)

Здесь напрашивается чисто формальное сопоставление с законом полного тока (13.1а): линии вектора А охватывают магнитный поток подобно тому, как линии вектора Н охватывают ток.

Общей задачей расчета магнитного поля постоянных токов является определение вектора напряженности магнитного поля или вектора магнитной индукции в каждой точке пространства по заданному распределению тока. Эта задача решается определением векторного потенциала как функции координат. Если сравнить уравнения Лапласа–Пуассона (13.13) и (13.15) для электростатики с уравнениями (13.51а, б), то легко заметить их очевидное сходство. Продолжая аналогию, можно частному решению для распределенных по объему зарядов из (13.31) сопоставить соответствующее выражение для проекции векторного потенциала:

,

где R – расстояние от элемента объема dV с током до точки, в которой определяется . Если ток I протекает по проводнику, размеры поперечного сечения которого S значительно меньше, чем расстояние R, то после замены ddV = dSdl = Idl можно найти векторный потенциал, создаваемый током такого провода длиной l:

, (13.54)

Кстати, из этого соотношения с учетом формулы (13.47) следует известный из курса физики закон Био–Савара:

(13.55)

Здесь 1R – единичный вектор, направленный вдоль R от элемента тока в рассматриваемую точку.

В областях, не занятых током, более простым может оказаться решение уравнения Лапласа для скалярного магнитного потенциала (13.49) с последующим использованием формулы (13.48). Разумеется, для этого подходят все методы, рассмотренные при исследовании электростатического поля.

Для выбора нужного решения уравнений в частных производных нужно знать граничные условия, в первую очередь на поверхности раздела сред с различными магнитными свойствами.