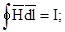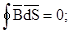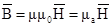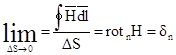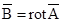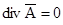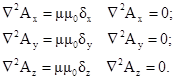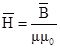Линии вектора магнитной индукции В всегда замкнуты.
Уравнения магнитного поля постоянного тока в интегральной форме
В основе расчета магнитного поля постоянных токов лежит следующая система уравнений в интегральной форме:
Эту систему следует дополнить выражением объемной плотности энергии магнитного поля
Первый интеграл известен под названием закона полного тока:
циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов, охватываемых контуром интегрирования.
Как известно, положительными считаются токи, направление которых образует правую винтовую систему с направлением обхода по контуру.
Второй интеграл выражает закон непрерывности магнитного потока:
линии вектора магнитной индукции В всегда замкнуты.
Связь между векторами B и H устанавливается третьим уравнением в котором m магнитная проницаемость вещества, а m0 магнитная постоянная. Н измеряется в амперах на метр, а В — в веберах на квадратный метр (в теслах). Следует напомнить, что уравнение, (3.3) применимо только для изотропных сред и является частным случаем соотношения, где вектор намагниченности пропорционален напряженности магнитного поля.
Из выражения удельной энергии магнитного поля (3.4) можно получить формулу для силы dFс которой магнитное поле действует на элемент тока Idl
dF=I[Bdl]
Формулу (3.5) часто рассматривают как уравнение, определяющее вектор В.
Уравнения (3.1) — (3.5) являются основой для расчёта магнитных цепей электромеханических устройств, в том числе и электрических машин.
Уравнения магнитного поля постоянного тока в дифференциальной форме
Уравнения поля в дифференциальной форме так же, как и граничные условия, получаются обычно из уравнений поля в интегральной форме путем предельного перехода к бесконечно малым величинам контура и поверхности интегрирования. Применим к элементарному контуру,
ограничивающему площадку DS, через которую проходит ток DIдля точек, где m непрерывно 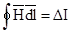
После деления обеих частей этого равенства на DS и перехода к пределу получится
или, учитывая, что проекции векторов равны независимо от
положения контура

Это и есть закон полного тока в дифференциальной форме.
Если вихрем вектора напряженности магнитного поля является вектор плотности свободных токов, то вихри вектора магнитной индукции определяются и свободными, и молекулярными токами
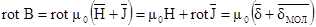
Применение уравнения , (3.9) к поверхности элементарной призмы объема DVприводит к выражению
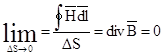
Это и есть закон непрерывности линий магнитной индукции в дифференциальной форме.Этот закон свидетельствует о чисто соленоидальном характере поля вектора В: не существует магнитных зарядов, которые служили бы началами и концами для линий магнитной индукции.
Иначе обстоит дело с вектором H. Из выражения

т.е. концы и начала линий вектора намагниченности являются началами и концами линий H. Так, например линии J начинаются на южном полюсе постоянного магнита и, не выходя за пределы магнита, заканчиваются на северном полюсе. Это и дает повод говорить об имеющих чисто расчетный смысл истоках и стоках вектора H как о “положительных магнитных массах” северного полюса, откуда линии Ннаправляются вне и внутри магнита к “отрицательным магнитным массам” южного полюса; так как внутри магнита линия H направлены против В, то принято говорить также о размагничивающем действии полюсов.
Граничные условия для векторов магнитного поля
Для точек, лежащих на поверхности раздела двух сред с различными значениями m, уравнения (3.1) и (3.2) при предельном переходе приводят к граничным условиям. Применим закон полного тока (2.1) к контуру элементарного прямоугольника (аналогичного изображенному на рис. 1.3), у которого основание — бесконечно малая первого порядка, высота—бесконечно малая второго порядка, а площадь, следовательно, бесконечно малая третьего порядка. Циркуляция вектора Н сведется к сумме двух слагаемых:

а полный ток, равный произведению средней плотности тока (конечной величины) на площадь прямоугольника,— к нулю. Таким образом, искомое граничное условие получается в виде
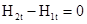
Если же применить закон непрерывности магнитного потока (3.2) к поверхности элементарной призмы (аналогичной изображенной на рис. 1.2), у которой площадь боковых граней бесконечно мала по сравнению с площадью оснований, то нетрудно получить граничное условие для нормальных составляющих вёкторов В1n и В2n:
Таким образом, в магнитном поле постоянных токов непрерывны, тангенциальные составляющие векторов Н и нормальные составляющие векторов В. Разумеется, Н и Вна границе сред с разными m меняются скачком, чем и обусловлено преломление магнитных линий.
Вектор-потенциал магнитного поля
Пуcть сформулирована следующая задача требуется рассчитать магнитное поле в однородной среде (m), если задано распределение плотности тока 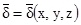
если плотность тока d задана в виде произвольной функции координат.
Введем новую векторную функцию А =А (х, у, z),позволяющую исключить неизвестные векторы Ви Низ уравнений (3.16) и получить взамен их дифференциальное уравнение, решение которого известно.
Такой подстановкой являетcя уравнение
удовлетворяющее требованию div B=0, так как дивергенция ротора тождественно равна нулю. Теперь можно исключить H из первого уравнения (3.16): _
Учитывая, что m = сопst; и что 
получаем
В полученном уравнении можно произвольно задаться значением 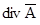
Действительно, если изменять величину дивергенции вектора, то будет меняться только величина потенциальной составляющей этого вектора, ротор от которой равен нулю. В рассматриваемом случае проще всего принять
В результате получается векторное уравнение Пуассона
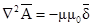
а для точек, где d = 0 —векторное уравнение Лапласа
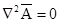
Каждое из этих векторных уравнений распадается на три скалярных уравнения:
Таким образом, определив А из уравнений (3.22) можно определить магнитную индукцию дифференцированием
Векторная функция A, с помощью которой решена поставленная задача, называется векторным потенциалом магнитного поля
Если среда состоит из различныхкусочно-однородных (в магнитном отношении областей” то решение системы (3.22) имеет свои особенности, поскольку в этом случае каждая область описывается своим вектор-потенциалом, который надо находить из уравнения Лапласа (если в области нет токов) либо из уравнения Пуассона. Отдельные решения должны удовлетворять граничным условиям (3.14 ) и (3.15).
Заметим, что граничное условие (3. 14) В1n=B2n удовлетворяется, если A1t=A2t. (это требование достаточное, но не необходнмое). Действительно, нормальная составляющая вектора В есть одновременно нормальная составляющая ротора А.Ноиз структуры дифференциального оператора rot A следует, что его нормальная к поверхности S составляющая определяется изменением вдоль этой поверхности касательных составляющих вектора А. Поэтому, если эти составляющие будут непрерывны, то непрерывны будут также нормальные составляющие rot A и B. В дальнейшем предполагается непрерывность тангенциальных составляющих вектор — потенциала.
Магнитное поле тока, магнитный ток.
Магнитное поле тока представляет собой силовое поле, воздействующее на электрические заряды и на тела, находящиеся в движении и имеющие магнитный момент, вне зависимости от состояния их движения. Магнитное поле является частью электромагнитного поля.
Ток заряженных частиц либо магнитные моменты электронов в атомах создают магнитное поле. Также, магнитное поле возникает в результате определенных временных изменений электрического поля.
Вектор индукции магнитного поля В представляет собой главную силовую характеристику магнитного поля. В математике В = В (X,Y,Z) определяется как векторное поле. Это понятие служит для определения и конкретизации физического магнитного поля. В науке зачастую вектор магнитной индукции попросту, для краткости, именуется магнитным полем. Очевидно, что такое применение допускает некоторую вольную трактовку этого понятия.
Ещё одной характеристикой магнитного поля тока есть векторные потенциал.
В научной литературе часто можно встретить, что в качестве главной характеристики магнитного поля, в условиях отсутствия магнитной среды (вакууме), рассматривается вектор напряжённости магнитного поля. Формально, такая ситуация вполне приемлема, поскольку в вакууме вектор напряженности магнитного поля H и вектор магнитной индукции B совпадают. В тоже время, вектор напряженности магнитного поля в магнитной среде не наполнен тем же физическим смыслом, и является второстепенной величиной. Исходя из этого при формальной равенства этих подходов для вакуума, систематическая точка зрения рассматривает вектор магнитной индукции основной характеристикой магнитного поля тока.
Магнитное поле, безусловно, представляет собой особенный вид материи. С помощью этой материи происходит взаимодействие между обладающими магнитным моментом и движущимися заряженными частицами либо телами.
Специальная теория относительности рассматривает магнитные поля как следствие существования самих электрических полей.
В совокупности магнитное и электрическое поля формируют электромагнитное поле. Проявлениями электромагнитного поля является свет и электромагнитные волны.
Квантовая теория магнитного поля рассматривает магнитное взаимодействие как отдельный случай электромагнитного взаимодействия. Он переносится безмассовым бозоном. Бозон представляет собой фотон — частицу, которую можно представить как квантовое возбуждение электромагнитного поля.
Порождается магнитное поле либо током заряженных частиц, либо трансформирующимся во временном пространстве электрическим полем, либо собственными магнитными моментами частиц. Магнитные моменты частиц для однообразного восприятия формально сводятся к электрическим токам.
Вычисление значения магнитного поля.
Простые случаи позволяют вычислить значения магнитного поля проводника с током по закону Био-Савара-Лапласа, либо при помощи теоремы о циркуляции. Таким же образом может быть найдено значение магнитного поля и для тока, произвольно распределённого в объёме или пространстве. Очевидно, эти законы применимы для постоянных либо относительно медленно изменяющихся магнитных и электрических полей. То есть, в случаях наличия магнитостатики. Более сложные случаи требуют вычисления значения магнитного поля тока согласно уравнений Максвелла.
Проявление наличия магнитного поля.
Основным проявлением магнитного поля является влияние на магнитные моменты частиц и тел, на заряженные частицы находящиеся в движении. Силой Лоренца называется сила, которая воздействует на электрически заряженную частицу, которая движется в магнитном поле. Эта сила имеет постоянно выраженную перпендикулярную направленность к векторам v и B. Она также имеет пропорциональное значение заряду частицы q, составляющей скорости v, осуществляющейся перпендикулярно направлению вектора магнитного поля B, и величине, которая выражает индукцию магнитного поля B. Сила Лоренца согласно Международной системе единиц имеет такое выражение: F = q [v, B], в системе единиц СГС: F = q / c [v, B]
Векторное произведение отображено квадратными скобками.
В результате влияния силы Лоренца на движущиеся по проводнику заряженные частицы, магнитное поле и может осуществлять воздействие на проводник с током. Силой Ампера является сила, действующая на проводник с током. Составляющими этой силы считаются силы, воздействующие на отдельные заряды, которые движутся внутри проводника.
Явление взаимодействия двух магнитов.
Явление магнитного поля, которое мы можем встретить в повседневной жизни, получило название взаимодействие двух магнитов. Оно выражается в отталкивании друг от друга одинаковых полюсов и притяжении противоположных полюсов. С формальной точки зрения описать взаимодействия между двумя магнитами как взаимодействие двух монополей, является достаточно полезной, реализуемой и удобной идеей. В то же время, детальный анализ свидетельствует, что в действительности это не совсем верное описание явления. Основным вопросом, остающимся без ответа в рамках такой модели, является, почему монополя не могут быть разделены. Собственно, экспериментально доказано, что любое изолированное тело не имеет магнитный заряд. Также эту модель невозможно применить к магнитному полю, созданному макроскопическим током.
С нашей точки зрения, правильно считать, что сила, действующая на магнитный диполь, находящийся в неоднородном поле, стремится развернуть его таким образом, чтобы магнитный момент диполя имел одинаковое с магнитным полем направление. Однако нет магнитов, которые подвержены воздействию суммарной силы со стороны однородного магнитного поля тока. Сила, которая действует на магнитный диполь с магнитным моментом m выражается следующей формулой:
.
Действующая на магнит сила со стороны неоднородного магнитного поля, выражается суммой всех сил, которые определяются данной формулой, и воздействующих на элементарные диполи, которые составляют магнит.
Электромагнитная индукция.
В случае изменения во времени потока вектора магнитной индукции через замкнутый контур, в этом контуре формируется ЭДС электромагнитной индукции. Если контур неподвижен, она порождается вихревым электрическим полем, которое возникает в результате изменения магнитного поля со временем. Когда магнитное поле не изменяется со временем и нет изменений потока из-за движения контура-проводника, то ЭДС порождается силой Лоренца.
Уравнения магнитного поля постоянных токов
3.3.1 нБЗОЙФОПЕ РПМЕ Й ЕЗП ИБТБЛФЕТЙУФЙЛЙ
чПЛТХЗ РТПЧПДОЙЛПЧ У ФПЛПН Й РПУФПСООЩИ НБЗОЙФПЧ УХЭЕУФЧХЕФ НБЗОЙФОПЕ РПМЕ. нБЗОЙФОПЕ РПМЕ ЕУФШ ЧЙД НБФЕТЙЙ, РПУТЕДУФЧПН ЛПФПТПЗП ЧЪБЙНПДЕКУФЧХАФ НЕЦДХ УПВПК ДЧЙЦХЭЙЕУС ЬМЕЛФТЙЮЕУЛЙЕ ЪБТСДЩ. пОП ЧПЪОЙЛБЕФ ЧПЛТХЗ МАВПЗП ОБРТБЧМЕООП ДЧЙЦХЭЕЗПУС ЬМЕЛФТЙЮЕУЛПЗП ЪБТСДБ, Б ФБЛЦЕ РТЙ ОБМЙЮЙЙ РЕТЕНЕООПЗП ЧП ЧТЕНЕОЙ ЬМЕЛФТЙЮЕУЛПЗП РПМС (Й Ч ЧБЛХХНЕ, Й Ч ДЙЬМЕЛФТЙЛБИ) Й ДЕКУФЧХЕФ ФПМШЛП ОБ ДЧЙЦХЭЙЕУС ЬМЕЛФТЙЮЕУЛЙЕ ЪБТСДЩ. оЕРПДЧЙЦОЩЕ ЪБТСДЩ НБЗОЙФОПЗП РПМС ОЕ УПЪДБАФ Й ОЕ ЙУРЩФЩЧБАФ УЙМПЧПЗП ЧПЪДЕКУФЧЙС УП УФПТПОЩ НБЗОЙФОПЗП РПМС.
нБЗОЙФОПЕ РПМЕ НПЦОП ПВОБТХЦЙФШ, РПНЕЭБС Ч ОЕЗП НБЗОЙФОЩЕ УФТЕМЛЙ ЙМЙ РТПЧПДОЙЛЙ У ФПЛПН, ФБЛ ЛБЛ ПОП ПЛБЪЩЧБЕФ ОБ ОЙИ ПТЙЕОФЙТХАЭЕЕ ДЕКУФЧЙЕ. нБЗОЙФОПЕ РПМЕ НПЦОП ЙУУМЕДПЧБФШ У РПНПЭША ЪБНЛОХФПЗП ЛПОФХТБ (ТБНЛЙ) У ФПЛПН. зЕПНЕФТЙЮЕУЛЙЕ ТБЪНЕТЩ ЛПОФХТБ ДПМЦОЩ ВЩФШ ОБУФПМШЛП НБМЩ, ЮФПВЩ Ч ЕЗП РТЕДЕМБИ РПМЕ ОЕ ЙЪНЕОСМПУШ. пТЙЕОФБГЙС ЛПОФХТБ Ч РТПУФТБОУФЧЕ ИБТБЛФЕТЙЪХЕФУС ОБРТБЧМЕОЙЕН ОПТНБМЙ Л ЛПОФХТХ. ч ЛБЮЕУФЧЕ РПМПЦЙФЕМШОПЗП ОБРТБЧМЕОЙС ОПТНБМЙ РТЙОЙНБЕФУС ОБРТБЧМЕОЙЕ, УЧСЪБООПЕ У ФПЛПН РТБЧЙМПН РТБЧПЗП ЧЙОФБ, Ф. Е. ЪБ РПМПЦЙФЕМШОПЕ ОБРТБЧМЕОЙЕ ОПТНБМЙ РТЙОЙНБЕФУС ОБРТБЧМЕОЙЕ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС ЧЙОФБ, ЗПМПЧЛБ ЛПФПТПЗП ЧТБЭБЕФУС Ч ОБРТБЧМЕОЙЙ ФПЛБ, ФЕЛХЭЕЗП Ч ТБНЛЕ. оБ ЛПОФХТ Ч НБЗОЙФОПН РПМЕ ДЕКУФЧХЕФ НЕИБОЙЮЕУЛЙК ЧТБЭБФЕМШОЩК НПНЕОФ. пФОПЫЕОЙЕ НБЛУЙНБМШОПЗП ЧТБЭБФЕМШОПЗП НПНЕОФБ нНБИ Л РТПЙЪЧЕДЕОЙА УЙМЩ ФПЛБ I, ФЕЛХЭЕЗП РП ЛПОФХТХ, Й РМПЭБДЙ РПЧЕТИОПУФЙ S, ПИЧБФЩЧБЕНПК ЬФЙН ЛПОФХТПН, ЧЕМЙЮЙОБ РПУФПСООБС:
ьФЙН ПФОПЫЕОЙЕН ПРТЕДЕМСЕФУС ПУОПЧОБС УЙМПЧБС ИБТБЛФЕТЙУФЙЛБ НБЗОЙФОПЗП РПМС — ЧЕЛФПТ НБЗОЙФОПК ЙОДХЛГЙЙ ч. рТПЙЪЧЕДЕОЙЕ I S ОБЪЩЧБЕФУС НБЗОЙФОЩН НПНЕОФПН ЛПОФХТБ У ФПЛПН:
оБРТБЧМЕОЙЕ НБЗОЙФОПЗП НПНЕОФБ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ЙОДХЛГЙЙ НБЗОЙФОПЗП РПМС, УПЪДБЧБЕНПЗП Ч ГЕОФТЕ ЛПОФХТБ ФЕЛХЭЙН РП ОЕНХ ФПЛПН. оБРТБЧМЕОЙЕ ЧЕЛФПТБ ч ПРТЕДЕМСЕФУС РП РТБЧЙМХ: ЕУМЙ ОБРТБЧМЕОЙЕ ЧТБЭЕОЙС ЧЙОФБ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ФПЛБ Ч ЛПОФХТЕ, ФП ЕЗП РПУФХРБФЕМШОПЕ ДЧЙЦЕОЙЕ ХЛБЦЕФ ОБРТБЧМЕОЙЕ ЙОДХЛГЙЙ НБЗОЙФОПЗП РПМС Й, УППФЧЕФУФЧЕООП, НБЗОЙФОПЗП НПНЕОФБ (ТЙУХОПЛ 3.27) (УМЕДУФЧЙЕ РТБЧЙМБ РТБЧПЗП ЧЙОФБ).

йФБЛ, ЧЕЛФПТ НБЗОЙФОПК ЙОДХЛГЙЙ ПРТЕДЕМСЕФУС НБЛУЙНБМШОЩН ЧТБЭБФЕМШОЩН НПНЕОФПН, ДЕКУФЧХАЭЙН ОБ ЛПОФХТ У ФПЛПН, НБЗОЙФОЩК НПНЕОФ ЛПФПТПЗП ТБЧЕО ЕДЙОЙГЕ:
 | (3.37) |
нБЗОЙФОБС ЙОДХЛГЙС ЙЪНЕТСЕФУС Ч ФЕУМБИ (фМ). фЕУМБ — ЬФП ЙОДХЛГЙС ФБЛПЗП ПДОПТПДОПЗП НБЗОЙФОПЗП РПМС, ЛПФПТПЕ ДЕКУФЧХЕФ У НБЛУЙНБМШОЩН ЧТБЭБФЕМШОЩН НПНЕОФПН 1о·Н ОБ ЛПОФХТ У ФПЛПН, НБЗОЙФОЩК НПНЕОФ ЛПФПТПЗП ТБЧЕО 1б·Н 2 .
йОДХЛГЙС НБЗОЙФОПЗП РПМС — ЬЛУРЕТЙНЕОФБМШОП ЙЪНЕТСЕНБС ЧЕМЙЮЙОБ, ЪБЧЙУСЭБС ПФ ФПЛПЧ, УПЪДБАЭЙИ РПМЕ, Й УЧПКУФЧ УТЕДЩ, Ч ЛПФПТПК ПОП УПЪДБОП.
нБЗОЙФОПЕ РПМЕ, ФБЛ ЦЕ ЛБЛ Й ЬМЕЛФТЙЮЕУЛПЕ, ЙЪПВТБЦБЕФУС УЙМПЧЩНЙ МЙОЙСНЙ, Ф.Е. МЙОЙСНЙ, ЛБУБФЕМШОБС Ч ЛБЦДПК ФПЮЛЕ ЛПФПТЩИ УПЧРБДБЕФ У ЧЕЛФПТПН НБЗОЙФОПК ЙОДХЛГЙЙ ч. пДОПТПДОПЕ НБЗОЙФОПЕ РПМЕ ЙЪПВТБЦБЕФУС РБТБММЕМШОЩНЙ МЙОЙСНЙ, ПФУФПСЭЙНЙ ОБ ТБЧОПН ТБУУФПСОЙЙ ДТХЗ ПФ ДТХЗБ. оБРТБЧМЕОЙЕ МЙОЙК НБЗОЙФОПК ЙОДХЛГЙЙ РПМС, УПЪДБООПЗП ФПЛПН, ПРТЕДЕМСЕФУС РП РТБЧЙМХ РТБЧПЗП ЧЙОФБ.
рТЙНЕТ 1. лЧБДТБФОБС ТБНЛБ УП УФПТПОПК 5 УН, ЙНЕАЭБС 10 ЧЙФЛПЧ, ОБИПДЙФУС Ч ПДОПТПДОПН НБЗОЙФОПН РПМЕ У ЙОДХЛГЙЕК 0,1 фМ. рМПУЛПУФШ ТБНЛЙ УПУФБЧМСЕФ ХЗПМ 0њУ ОБРТБЧМЕОЙЕН НБЗОЙФОПЗП РПМС. пРТЕДЕМЙФШ ЧТБЭБАЭЙК НПНЕОФ УЙМ, ДЕКУФЧХАЭЙИ ОБ ТБНЛХ, ЕУМЙ ФПЛ Ч ТБНЛЕ ТБЧЕО 4б.
Б = 5 УН (5ћ 10 -2 Н),
тЕЫЕОЙЕ. нЕИБОЙЮЕУЛЙК НПНЕОФ УЙМ, ДЕКУФЧХАЭЙК ОБ ТБНЛХ, ПРТЕДЕМСЕФУС ЙЪ ЖПТНХМЩ (3.37), Й ФБЛ ЛБЛ ТБНЛБ УПУФПЙФ ЙЪ N ЧЙФЛПЧ НПЦОП ЪБРЙУБФШ
нЧТ = N I S B sin Б,
ЗДЕ S = Б 2 — РМПЭБДШ ТБНЛЙ, Б = π /2 — ХЗПМ НЕЦДХ ОПТНБМША Л РМПУЛПУФЙ ТБНЛЙ Й ОБРТБЧМЕОЙЕН НБЗОЙФОПЗП РПМС. йНЕЕН
нЧТ = 10 ћ 4 ћ 25 ћ 10 -4 ћ0,1 (о ћ Н) = 10 -2 о ћ Н
оБТСДХ У ЧЕЛФПТПН НБЗОЙФОПК ЙОДХЛГЙЙ ч ЧЧПДЙФУС ЕЭЕ ПДОБ УЙМПЧБС ИБТБЛФЕТЙУФЙЛБ НБЗОЙФОПЗП РПМС — ОБРТСЦЕООПУФШ НБЗОЙФОПЗП РПМС о. чЕЛФПТЩ ч Й о УЧСЪБОЩ УППФОПЫЕОЙЕН
 | (3.38) |
оБРТСЦЕООПУФШ НБЗОЙФОПЗП РПМС ЙЪНЕТСЕФУС Ч БНРЕТБИ ОБ НЕФТ (б/Н), μ0 — НБЗОЙФОБС РПУФПСООБС, ТБЧОБС μ0 = 4 π· 10 -7 зО/Н, μ — ПФОПУЙФЕМШОБС НБЗОЙФОБС РТПОЙГБЕНПУФШ УТЕДЩ, РПЛБЪЩЧБАЭБС, ЧП УЛПМШЛП ТБЪ ЙОДХЛГЙС НБЗОЙФОПЗП РПМС Ч ДБООПК УТЕДЕ ВПМШЫЕ ЙМЙ НЕОШЫЕ, ЮЕН Ч ЧБЛХХНЕ. оБРТСЦЕООПУФШ НБЗОЙФОПЗП РПМС ПРТЕДЕМСЕФУС ФПМШЛП ЛПОЖЙЗХТБГЙЕК РТПЧПДОЙЛПЧ, УПЪДБАЭЙИ РПМЕ, Й ФПЛБНЙ, ФЕЛХЭЙНЙ РП ЬФЙН РТПЧПДОЙЛБН, Ф. Е. НБЛТПЙУФПЮОЙЛБНЙ РПМС, Й ОЕ ЪБЧЙУЙФ ПФ НБЗОЙФОЩИ УЧПКУФЧ УТЕДЩ, Ч ЛПФПТПК РПМЕ УПЪДБЕФУС.
3.3.2 нБЗОЙФОПЕ РПМЕ ФПЛПЧ ТБЪМЙЮОПК ЛПОЖЙЗХТБГЙЙ
йОДХЛГЙС НБЗОЙФОПЗП РПМС, УПЪДБЧБЕНПЗП РТПЧПДОЙЛБНЙ У ФПЛПН ТБЪМЙЮОПК ЛПОЖЙЗХТБГЙЙ, ПРТЕДЕМСЕФУС РП ЪБЛПОХ вЙП — уБЧБТБ — мБРМБУБ. дБМШОЕКЫЙЕ ЖПТНХМЩ РТЙЧПДЙН ВЕЪ ЧЩЧПДБ.
1) йОДХЛГЙС НБЗОЙФОПЗП РПМС, УПЪДБЧБЕНПЗП ВЕУЛПОЕЮОЩН РТСНЩН РТПЧПДОЙЛПН У ФПЛПН (ТЙУХОПЛ 3.28.), ТБЧОБ:
 тЙУХОПЛ 3.28 |  | (3.39) |
2) йОДХЛГЙС НБЗОЙФОПЗП РПМС Ч ГЕОФТЕ ЛТХЗПЧПЗП ЧЙФЛБ У ФПЛПН (ТЙУХОПЛ 3.29)
 тЙУХОПЛ 3.29 |  | (3.40) |
ЗДЕ З — ТБДЙХУ ЧЙФЛБ.
3) йОДХЛГЙС НБЗОЙФОПЗП РПМС Ч ГЕОФТЕ УПМЕОПЙДБ (ЧДБМЙ ПФ ЛТБЕЧ УПМЕОПЙДБ, ЗДЕ РПМЕ УХЭЕУФЧЕООП ОЕПДОПТПДОП) ТБЧОБ (ТЙУХОПЛ 3.30):
 тЙУХОПЛ 3.30 |  |
ЗДЕ n — ЮЙУМП ЧЙФЛПЧ, РТЙИПДСЭЕЕУС ОБ ЕДЙОЙГХ ДМЙОЩ УПМЕОПЙДБ.
еУМЙ РПМЕ УПЪДБЕФУС ОЕУЛПМШЛЙНЙ ЙУФПЮОЙЛБНЙ, ФП ЧЕЛФПТ НБЗОЙФОПК ЙОДХЛГЙЙ Ч ДБООПК ФПЮЛЕ ПРТЕДЕМСЕФУС, ЛБЛ ЧЕЛФПТОБС УХННБ ЧЕЛФПТПЧ НБЗОЙФОПК ЙОДХЛГЙЙ РПМЕК, УПЪДБЧБЕНЩИ ЛБЦДЩН ЙУФПЮОЙЛПН Ч ПФДЕМШОПУФЙ чi, (РТЙОГЙР УХРЕТРПЪГЙЙ):
ъБНЕФЙН, ЮФП УЙМПЧЩЕ МЙОЙЙ НБЗОЙФОПЗП РПМС ЪБНЛОХФЩ, ФБЛ ЛБЛ Ч РТЙТПДЕ ОЕ УХЭЕУФЧХЕФ РПМПЦЙФЕМШОЩИ Й ПФТЙГБФЕМШОЩИ НБЗОЙФОЩИ ЪБТСДПЧ.
рТЙНЕТ 1. лТХЗПЧПК ЧЙФПЛ ТБДЙХУБ r, РП ЛПФПТПНХ ФЕЮЕФ ФПЛ I2, ОБИПДЙФУС ЧВМЙЪЙ ВЕУЛПОЕЮОПЗП РТСНПЗП РТПЧПДБ, РП ЛПФПТПНХ ФЕЮЕФ ФПЛ I1 . рТПЧПДОЙЛ Й ЧЙФПЛ МЕЦБФ Ч ПДОПК РМПУЛПУФЙ (ТЙУХОПЛ 3.31). тБУУФПСОЙЕ ПФ ГЕОФТБ ЧЙФЛБ ДП РТПЧПДОЙЛБ ТБЧОП 2r. пРТЕДЕМЙФЕ ЙОДХЛГЙА НБЗОЙФОПЗП РПМС Ч ГЕОФТЕ ЧЙФЛБ. лБЛ ДПМЦОБ ЙЪНЕОЙФШУС УЙМБ ФПЛБ I2, ЮФПВЩ ЙОДХЛГЙС НБЗОЙФОПЗП РПМС Ч ГЕОФТЕ ЧЙФЛБ УФБМБ ТБЧОБ ОХМА?
 тЙУХОПЛ 3.31
тЙУХОПЛ 3.31тЕЫЕОЙЕ. нБЗОЙФОПЕ РПМЕ УПЪДБЕФУС РТСНЩН РТПЧПДОЙЛПН У ФПЛПН Й ЛТХЗПЧЩН ЧЙФЛПН. чЕЛФПТ ЙОДХЛГЙЙ РПМС B1, УПЪДБЧБЕНПЗП РТСНЩН РТПЧПДОЙЛПН У ФПЛПН (ТЙУХОПЛ 3.31), МЕЦЙФ Ч РМПУЛПУФЙ ЮЕТФЕЦБ. чЕЛФПТ ЙОДХЛГЙЙ НБЗОЙФОПЗП РПМС ЧЙФЛБ У ФПЛПН ч2 ФБЛЦЕ РЕТРЕОДЙЛХМСТЕО РМПУЛПУФЙ ЧЙФЛБ. уПЗМБУОП РТЙОГЙРХ УХРЕТРПЪЙГЙЙ РПМЕК, ч = B1 + B2, ЙМЙ Ч РТПЕЛГЙЙ ОБ ПУШ Х:
йОДХЛГЙС НБЗОЙФОПЗП РПМС Ч ГЕОФТЕ ЧЙФЛБ ПВТБЭБЕФУС Ч ОХМШ, ЕУМЙ I1 = I’2/2π, ПФЛХДБ I’2 = 2πI1. уЙМБ ФПЛБ, ФЕЛХЭЕЗП РП РТСНПНХ РТПЧПДОЙЛХ, ДПМЦОБ ЙЪНЕОЙФШУС ОБ ЧЕМЙЮЙОХ I1= I’2 — I1 = 2 πI1 — I1.
3.3.3 ъБЛПО бНРЕТБ
рПНЕУФЙН Ч НБЗОЙФОПЕ РПМЕ РТПЧПДОЙЛ ДМЙОПК L, РП ЛПФПТПНХ ФЕЮЕФ ФПЛ I (ТЙУХОПЛ 3.32).

оБ РТПЧПДОЙЛ ДЕКУФЧХЕФ УЙМБ, РТСНП РТПРПТГЙПОБМШОБС УЙМЕ ФПЛБ, ФЕЛХЭЕЗП РП РТПЧПДОЙЛХ, ЙОДХЛГЙЙ НБЗОЙФОПЗП РПМС, ДМЙОЕ РТПЧПДОЙЛБ, Й ЪБЧЙУСЭБС ПФ ПТЙЕОФБГЙЙ РТПЧПДОЙЛБ Ч НБЗОЙФОПН РПМЕ. ъБЛПО бНРЕТБ:
| |F| = I B L sin α | (3.41) |
ЗДЕ α — ХЗПМ НЕЦДХ ОБРТБЧМЕОЙЕН ФПЛБ Ч РТПЧПДОЙЛЕ Й ОБРТБЧМЕОЙЕН ЧЕЛФПТБ НБЗОЙФОПК ЙОДХЛГЙЙ ч.
оБРТБЧМЕОЙЕ УЙМЩ бНРЕТБ ПРТЕДЕМСЕФУС РП РТБЧЙМХ МЕЧПК ТХЛЙ: ЕУМЙ МЕЧХА ТХЛХ ТБУРПМПЦЙФШ ФБЛ, ЮФП НБЗОЙФОЩЕ УЙМПЧЩЕ МЙОЙЙ ЧИПДСФ Ч МБДПОШ, ЮЕФЩТЕ ЧЩФСОХФЩИ РБМШГБ ОБРТБЧЙФШ РП ФПЛХ, ФП ПФПЗОХФЩК ВПМШЫПК РБМЕГ ХЛБЦЕФ ОБРТБЧМЕОЙЕ УЙМЩ. пЮЕЧЙДОП, ЮФП УЙМБ бНРЕТБ ТБЧОБ ОХМА, ЕУМЙ РТПЧПДОЙЛ ТБУРПМПЦЕО ЧДПМШ УЙМПЧЩИ МЙОЙК РПМС Й НБЛУЙНБМШОБ, ЕУМЙ РТПЧПДОЙЛ РЕТРЕОДЙЛХМСТЕО УЙМПЧЩН МЙОЙСН.
рТЙНЕТ 1. ч ПДОПТПДОПН НБЗОЙФОПН РПМЕ, ЙОДХЛГЙС ЛПФПТПЗП ТБЧОБ 4ћ10 -2 фМ Й ОБРТБЧМЕОБ РПД ХЗМПН β = 30њ Л ЧЕТФЙЛБМЙ, РП ЧЕТФЙЛБМШОЩН РТПЧПДБН ВЕЪ ФТЕОЙС ЧЧЕТИ ДЧЙЦЕФУС РТСНПК РТПЧПДОЙЛ НБУУПК 10 З, РП ЛПФПТПНХ ФЕЮЕФ ФПЛ 3 б. юЕТЕЪ 5 У РПУМЕ ОБЮБМБ ДЧЙЦЕОЙС РТПЧПДОЙЛ ЙНЕЕФ УЛПТПУФШ 20 Н/У. пРТЕДЕМЙФШ ДМЙОХ РТПЧПДОЙЛБ.
I = 3 б, t = 5У, v = 20 Н/У;
тЕЫЕОЙЕ. оБ РТПЧПДОЙЛ У ФПЛПН, РПНЕЭЕООЩК Ч НБЗОЙФОПЕ РПМЕ, ДЕКУФЧХЕФ УЙМБ бНРЕТБ |F| = I B L sin α, ЗДЕ α = π /2, ОБРТБЧМЕООБС, ЛБЛ ХЛБЪБОП ОБ ТЙУХОЛЕ 3.33.

дЧЙЦЕОЙЕ РТПЧПДОЙЛБ ПУХЭЕУФЧМСЕФУС ФПМШЛП Ч ЧЕТФЙЛБМШОПН ОБРТБЧМЕОЙЙ. хУЛПТЕОЙЕ РТПЧПДОЙЛБ ОБКДЕН ЙЪ ЧФПТПЗП ЪБЛПОБ оШАФПОБ mБ = FAX — mg, ЗДЕ FAX — FA COS 60њ — РТПЕЛГЙС УЙМЩ бНРЕТБ ОБ ЧЕТФЙЛБМШОХА ПУШ:
mБ = FA cos 60њ — mg = I B l cos 60њ — mg
уЛПТПУФШ РТПЧПДОЙЛБ ТБЧОБ
3.3.4 чЪБЙНПДЕКУФЧЙЕ ДЧХИ РТСНПМЙОЕКОЩИ РТПЧПДОЙЛПЧ У ФПЛПН
рХУФШ РП ДЧХН РБТБММЕМШОЩН РТПЧПДОЙЛБН, ПФУФПСЭЙН ДТХЗ ПФ ДТХЗБ ОБ ТБУУФПСОЙЙ d, ФЕЛХФ ФПЛЙ Ч ПДОПН ОБРТБЧМЕОЙЙ I1 Й I2 (ТЙУХОПЛ 3.34).
тБУУНПФТЙН РТПЧПДОЙЛ 2 Ч РПМЕ РТПЧПДОЙЛБ У ФПЛПН I1. йОДХЛГЙС НБЗОЙФОПЗП РПМС, УПЪДБООПЗП РТПЧПДОЙЛПН У ФПЛПН I1 ОБ ТБУУФПСОЙЙ d,УПЗМБУОП (3.39), ТБЧОБ
рП ЪБЛПОХ бНРЕТБ ОБ РТПЧПДОЙЛ 2 ДЕКУФЧХЕФ УЙМБ:
ЗДЕ Δl — ЬМЕНЕОФ ДМЙОЩ РТПЧПДОЙЛБ 2:
 | (3.42) |
оБ ФБЛПК ЦЕ ЬМЕНЕОФ ДМЙОЩ РТПЧПДОЙЛБ 1 ДЕКУФЧХЕФ УЙМБ, ТБЧОБС РП ЧЕМЙЮЙОЕ (3.42) Й РТПФЙЧПРПМПЦОБС РП ОБРТБЧМЕОЙА.
рПУЛПМШЛХ ЪБЛПО (3.42) МЕЗЛП РТПЧЕТЙФШ ПРЩФОЩН РХФЕН, ФП ЙЪ ОЕЗП НПЦЕФ ВЩФШ ЧЩЧЕДЕОБ ПУОПЧОБС ЬМЕЛФТЙЮЕУЛБС ЕДЙОЙГБ уй — БНРЕТ. 1 БНРЕТ — ЬФП УЙМБ ФБЛПЗП ФПЛБ, РТЙ РТПФЕЛБОЙЙ ЛПФПТПЗП РП ДЧХН ВЕУЛПОЕЮОЩН РБТБММЕМШОЩН РТПЧПДОЙЛБН ОЙЮФПЦОП НБМПЗП УЕЮЕОЙС, ТБУРПМПЦЕООЩН ДТХЗ ПФ ДТХЗБ ОБ ТБУУФПСОЙЙ 1 Н Ч ЧБЛХХНЕ, РТПЧПДОЙЛЙ ЧЪБЙНПДЕКУФЧХАФ У УЙМПК 2 · 10 -7 о ОБ ЛБЦДЩК НЕФТ ДМЙОЩ РТПЧПДОЙЛБ. йЪ ТЙУХОЛБ УМЕДХЕФ, ЮФП ФПЛЙ, ФЕЛХЭЙЕ Ч ПДОПН ОБРТБЧМЕОЙЙ, РТЙФСЗЙЧБАФУС, Ч РТПФЙЧПРПМПЦОЩИ — ПФФБМЛЙЧБАФУС.
3.3.5 дЧЙЦЕОЙЕ ЪБТСЦЕООЩИ ЮБУФЙГ Ч НБЗОЙФОПН РПМЕ
рХУФШ РП ДЧХН РБТБММЕМШОЩН РТПЧПДОЙЛБН, ПФУФПСЭЙН ДТХЗ ПФ ДТХЗБ ОБ ТБУУФПСОЙЙ d, ФЕЛХФ ФПЛЙ Ч ПДОПН ОБРТБЧМЕОЙЙ I1 Й I2 (ТЙУХОПЛ 3.34).
оБ РТПЧПДОЙЛ У ФПЛПН Ч НБЗОЙФОПН РПМЕ ДЕКУФЧХЕФ УЙМБ бНРЕТБ Fб = I B sin α. фПЛ, Ч УЧПА ПЮЕТЕДШ, ЬФП ОБРТБЧМЕООПЕ ДЧЙЦЕОЙЕ ЪБТСЦЕООЩИ ЮБУФЙГ. уЙМБ ФПЛБ ТБЧОБ I = q n v S, ЗДЕ q — ЪБТСД ЮБУФЙГЩ, n — ЛПОГЕОФТБГЙС ДЧЙЦХЭЙИУС ЪБТСЦЕООЩИ ЮБУФЙГ, v — УТЕДОСС УЛПТПУФШ ЙИ ОБРТБЧМЕООПЗП ДЧЙЦЕОЙС, S — РМПЭБДШ РПРЕТЕЮОПЗП УЕЮЕОЙС РТПЧПДОЙЛБ. рПДУФБЧЙЧ I Ч ЧЩТБЦЕОЙЕ ДМС Fб, РПМХЮЙН Fб = q n v S I B sin α, ЗДЕ n S l = N — ПВЭЕЕ ЮЙУМП ЮБУФЙГ, УПЪДБАЭЙИ ФПЛ. фПЗДБ УЙМБ, ДЕКУФЧХАЭБС ОБ ПФДЕМШОЩК ДЧЙЦХЭЙКУС ЪБТСД — УЙМБ мПТЕОГБ, ТБЧОБ
| FМ = q v B sin α | (3.43) |
ЗДЕ α ХЗПМ НЕЦДХ ЧЕЛФПТБНЙ УЛПТПУФЙ Й НБЗОЙФОПК ЙОДХЛГЙЙ.
оБРТБЧМЕОЙЕ УЙМЩ мПТЕОГБ ПРТЕДЕМСЕФУС ДМС РПМПЦЙФЕМШОП ЪБТСЦЕООПК ЮБУФЙГЩ РП РТБЧЙМХ МЕЧПК ТХЛЙ. еУМЙ МЕЧХА ТХЛХ ТБУРПМПЦЙФШ ФБЛ, ЮФП УЙМПЧЩЕ МЙОЙЙ РПМС ЧИПДСФ Ч МБДПОШ, ЧЩФСОХФЩЕ ЮЕФЩТЕ РБМШГБ ОБРТБЧМЕОЩ ЧДПМШ УЛПТПУФЙ, ФП ПФПЗОХФЩК ВПМШЫПК РБМЕГ ХЛБЦЕФ ОБРТБЧМЕОЙЕ УЙМЩ мПТЕОГБ. дМС ЮБУФЙГЩ У ПФТЙГБФЕМШОЩН ЪБТСДПН ОБРТБЧМЕОЙЕ УЙМЩ РТПФЙЧПРПМПЦОП. йЪ ЖПТНХМЩ (3.43) ДМС УЙМЩ мПТЕОГБ УМЕДХЕФ, ЮФП НБЗОЙФОПЕ РПМЕ ОЕ ДЕКУФЧХЕФ 1) ОБ ОЕРПДЧЙЦОХА ЮБУФЙГХ (РТЙ v = 0 Fм = 0); 2) ОБ ОЕКФТБМШОХА ЮБУФЙГХ (РТЙ q = 0 Fм = 0); 3) ЕУМЙ УЛПТПУФШ ЮБУФЙГЩ ОБРТБЧМЕОБ ЧДПМШ МЙОЙК ЙОДХЛГЙЙ РПМС (РТЙ α = 0, π, Fм = 0). фБЛ ЛБЛ УЙМБ мПТЕОГБ ОБРТБЧМЕОБ РЕТРЕОДЙЛХМСТОП УЛПТПУФЙ, ФП ЬФБ УЙМБ ОЕ ЙЪНЕОСЕФ ЧЕМЙЮЙОЩ УЛПТПУФЙ, Б ЙЪНЕОСЕФ ФПМШЛП ЕЕ ОБРТБЧМЕОЙЕ, ЮБУФЙГБ ДЧЙЦЕФУС У ГЕОФТПУФТЕНЙФЕМШОЩН (ОПТНБМШОЩН) ХУЛПТЕОЙЕН БР.
рХУФШ ЪБТСЦЕООБС ЮБУФЙГБ, НБУУБ Й ЪБТСД ЛПФПТПК Ф Й q, ЧМЕФБЕФ РЕТРЕОДЙЛХМСТОП ЧЕЛФПТХ ч УП УЛПТПУФША v. оБ ЮБУФЙГХ ДЕКУФЧХЕФ УЙМБ мПТЕОГБ Fм = q v B. пУОПЧОПК ЪБЛПО ДЙОБНЙЛЙ ДМС ЮБУФЙГЩ, ДЧЙЦХЭЕКУС РП ПЛТХЦОПУФЙ, ЙНЕЕФ ЧЙД:
ПФЛХДБ ТБДЙХУ ПЛТХЦОПУФЙ, РП ЛПФПТПК ДЧЙЦЕФУС ЮБУФЙГБ, ТБЧЕО
 | (3.44) |
лБЛ ЧЙДЙН, Ч ПДОПТПДОПН НБЗОЙФОПН РПМЕ R = const Й, УМЕДПЧБФЕМШОП, ФТБЕЛФПТЙС ЮБУФЙГЩ — ДХЗБ ПЛТХЦОПУФЙ. рЕТЙПД ДЧЙЦЕОЙС ЮБУФЙГЩ РП ПЛТХЦОПУФЙ ТБЧЕО
уЙМБ мПТЕОГБ ЧУЕЗДБ РЕТРЕОДЙЛХМСТОБ УЛПТПУФЙ, Б УМЕДПЧБФЕМШОП, Й ЬМЕНЕОФБТОПНХ РЕТЕНЕЭЕОЙА. рПЬФПНХ ТБВПФБ УЙМЩ мПТЕОГБ ТБЧОБ ОХМА.
еУМЙ ЮБУФЙГБ ЧМЕФБЕФ РПД ХЗМПН α Л МЙОЙСН ЙОДХЛГЙЙ НБЗОЙФОПЗП РПМС (ТЙУХОПЛ 3.35), ФП ПОБ ХЮБУФЧХЕФ Ч УМПЦОПН ДЧЙЦЕОЙЙ.

тБЪМПЦЙН ЧЕЛФПТ УЛПТПУФЙ ОБ ДЧЕ УПУФБЧМСАЭЙЕ v|| Й v┴, ПЮЕЧЙДОП, ЮФП ЮБУФЙГБ ВХДЕФ ДЧЙЗБФШУС ТБЧОПНЕТОП ЧДПМШ УЙМПЧЩИ МЙОЙК НБЗОЙФОПЗП РПМС УП УЛПТПУФША v|| (ОБ ЮБУФЙГХ, ДЧЙЦХЭХАУС ЧДПМШ УЙМПЧЩИ МЙОЙК, НБЗОЙФОПЕ РПМЕ ОЕ ДЕКУФЧХЕФ) Й ТБЧОПНЕТОП ДЧЙЗБФШУС РП ПЛТХЦОПУФЙ УП УЛПТПУФША v┴ Ч РМПУЛПУФСИ, РЕТРЕОДЙЛХМСТОЩИ ЧЕЛФПТХ ч (ОБ ЮБУФЙГХ ДЕКУФЧХЕФ УЙМБ мПТЕОГБ Fм = q v┴ B). ч ТЕЪХМШФБФЕ УМПЦЕОЙС ЬФЙИ ДЧЙЦЕОЙК ЮБУФЙГБ ВХДЕФ ДЧЙЗБФШУС РП ЧЙОФПЧПК МЙОЙЙ.
рТЙНЕТ 1. рТПФПО ЧМЕФБЕФ Ч ПВМБУФШ ПДОПТПДОПЗП НБЗОЙФОПЗП РПМС ЫЙТЙОПК l, ЙОДХЛГЙС НБЗОЙФОПЗП РПМС ч. уЛПТПУФШ РТПФПОБ РЕТРЕОДЙЛХМСТОБ ЙОДХЛГЙЙ РПМС ч Й ЗТБОЙГЕ ПВМБУФЙ. рПД ЛБЛЙН ХЗМПН α Л РЕТЧПОБЮБМШОПНХ ОБРТБЧМЕОЙА ДЧЙЦЕОЙС РТПФПО ЧЩМЕФЙФ ЙЪ ПВМБУФЙ РПМС?
тЕЫЕОЙЕ: йЪ ТЙУХОЛБ 3.36 УМЕДХЕФ, ЮФП УЙОХУ ЙУЛПНПЗП ХЗМБ α ТБЧЕО sin α = l/R, ЗДЕ R — ТБДЙХУ ПЛТХЦОПУФЙ, РП ЛПФПТПК ДЧЙЦЕФУС РТПФПО Ч НБЗОЙФОПН РПМЕ.

тЙУХОПЛ 3.36
рП ЖПТНХМЕ (3.44) ПРТЕДЕМЙН ТБДЙХУ ФТБЕЛФПТЙЙ ДЧЙЦЕОЙС РТПФПОБ:
рТЙНЕТ 2. ьМЕЛФТПО ДЧЙЦЕФУС Ч ПДОПТПДОПН НБЗОЙФОПН РПМЕ У ЙОДХЛГЙЕК 10 -2 фМ. ч ОЕЛПФПТЩК НПНЕОФ ЧЕЛФПТ ЕЗП УЛПТПУФЙ, ТБЧОПК 10 6 Н/У, УПУФБЧМСЕФ ХЗПМ 30њ У ОБРТБЧМЕОЙЕН НБЗОЙФОПЗП РПМС. чЩЮЙУМЙФШ ТБДЙХУ R Й ЫБЗ h ЧЙОФПЧПК МЙОЙЙ, РП ЛПФПТПК ДЧЙЦЕФУС ЬМЕЛФТПО. нБУУБ ЬМЕЛФТПОБ mЕ = 9,1ћ 10 -31 ЛЗ, ЕЗП ЪБТСД qe = — 1,6ћ10 -19 лМ.
qe = — 1,6 ћ 10 -19 лМ;
тЕЫЕОЙЕ: чПУРПМШЪХЕНУС ЪБЛПОПН ОЕЪБЧЙУЙНПУФЙ ДЧЙЦЕОЙК Й ВХДЕН ТБУУНБФТЙЧБФШ УМПЦОПЕ ДЧЙЦЕОЙЕ ЛБЛ УХННХ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙК ЧДПМШ УЙМПЧЩИ МЙОЙК НБЗОЙФОПЗП РПМС Й Ч РМПУЛПУФЙ, РЕТРЕОДЙЛХМСТОПК ОБРТБЧМЕОЙА МЙОЙК ЙОДХЛГЙЙ. тБЪМПЦЙН ЧЕЛФПТ УЛПТПУФЙ ЬМЕЛФТПОБ v ОБ ДЧЕ УПУФБЧМСАЭЙЕ — ЧДПМШ НБЗОЙФОПЗП РПМС v|| Й РЕТРЕОДЙЛХМСТОП ЕНХ v┴ : v|| = v cos α, v┴ = v sin α (ТЙУХОПЛ 3.35). чДПМШ РПМС ЬМЕЛФТПО ДЧЙЦЕФУС ТБЧОПНЕТОП. оБ ЮБУФЙГХ ДЕКУФЧХЕФ УЙМБ мПТЕОГБ, ТБЧОБС FМ = q v┴ B. рПД ДЕКУФЧЙЕН ЬФПК УЙМЩ ЮБУФЙГБ ДЧЙЦЕФУС РП ПЛТХЦОПУФЙ, Ч РМПУЛПУФЙ, РЕТРЕОДЙЛХМСТОПК ОБРТБЧМЕОЙА РПМС, У РЕТЙПДПН ф. ч ТЕЪХМШФБФЕ УМПЦЕОЙС ЬФЙИ ДЧЙЦЕОЙС ЮБУФЙГБ ВХДЕФ ДЧЙЗБФШУС РП ЧЙОФПЧПК МЙОЙЙ, РТЙЮЕН ТБДЙХУ ПЛТХЦОПУФЙ ТБЧЕО:
ъБ ЧТЕНС, ТБЧОПЕ РЕТЙПДХ, ЮБУФЙГБ ЧДПМШ РПМС РТПИПДЙФ РХФШ h (ЫБЗ ЧЙОФПЧПК МЙОЙЙ):h = vIIT = (v cosα)2πme/qeB. рПДУФБЧЙЧ ЮЙУМЕООЩЕ ДБООЩЕ РПМХЮЙН:
3.3.6 нБЗОЙФОЩК РПФПЛ
нБЗОЙФОЩН РПФПЛПН ж ЮЕТЕЪ ОЕЛПФПТХА РПЧЕТИОПУФШ S (ТЙУХОПЛ 3.37) ОБЪЩЧБЕФУС УЛБМСТОБС ЧЕМЙЮЙОБ, ТБЧОБС РТПЙЪЧЕДЕОЙА НПДХМС ЧЕЛФПТБ НБЗОЙФОПК ЙОДХЛГЙЙ ОБ РМПЭБДШ ЬФПК РПЧЕТИОПУФЙ Й ЛПУЙОХУ ХЗМБ НЕЦДХ ОПТНБМША n Л ОЕК Й ОБРТБЧМЕОЙЕН ЧЕЛФПТБ НБЗОЙФОПК ЙОДХЛГЙЙ ч:
| ж = B S cosα = чn S | (3.45) |
ЗДЕ α — ХЗПМ НЕЦДХ ОБРТБЧМЕОЙСНЙ ЧЕЛФПТПЧ n Й ч, чn — РТПЕЛГЙС ЧЕЛФПТБ ч ОБ ОПТНБМШ.

еУМЙ НБЗОЙФОПЕ РПМЕ ОЕПДОПТПДОП, ФП РПЧЕТИОПУФШ S ТБЪВЙЧБАФ ОБ ЬМЕНЕОФБТОЩЕ РМПЭБДЛЙ ΔSi, (ТЙУХОПЛ 3.38), Ч РТЕДЕМБИ ЛБЦДПК ЙЪ ЛПФПТЩИ РПМЕ НПЦОП УЮЙФБФШ ПДОПТПДОЩН.

фПЗДБ РПМОЩК РПФПЛ ЮЕТЕЪ ЬФХ РПЧЕТИОПУФШ ТБЧЕО УХННЕ РПФПЛПЧ ЧЕЛФПТБ НБЗОЙФОПК ЙОДХЛГЙЙ ЮЕТЕЪ ЬМЕНЕОФБТОЩЕ РМПЭБДЛЙ:
дМС ВЕУЛПОЕЮОП НБМЩИ ЧЕМЙЮЙО НПЦОП ЪБРЙУБФШ:
ч уй ЕДЙОЙГЕК НБЗОЙФОПЗП РПФПЛБ СЧМСЕФУС 1 ЧЕВЕТ (чВ)- НБЗОЙФОЩК РПФПЛ ЮЕТЕЪ РПЧЕТИОПУФШ РМПЭБДША 1Н2, ТБУРПМПЦЕООХА РЕТРЕОДЙЛХМСТОП ОБРТБЧМЕОЙА ПДОПТПДОПЗП НБЗОЙФОПЗП РПМС, ЙОДХЛГЙС ЛПФПТПЗП ТБЧОБ 1 фМ:
http://www.calc.ru/Magnitnoye-Pole-Toka-Magnitniy-Tok.html
http://cde.osu.ru/courses2/course120/4_2.html