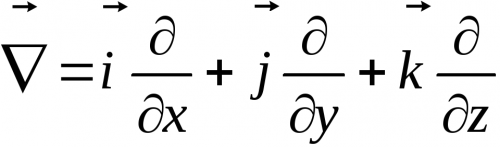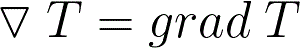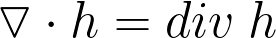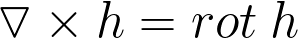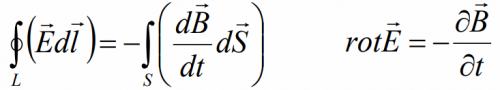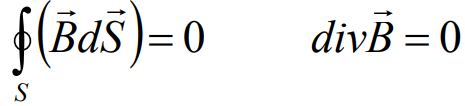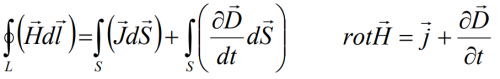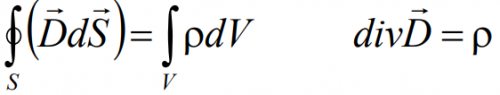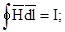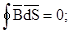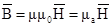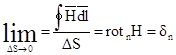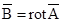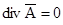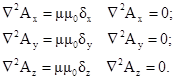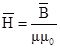Уравнения Максвелла

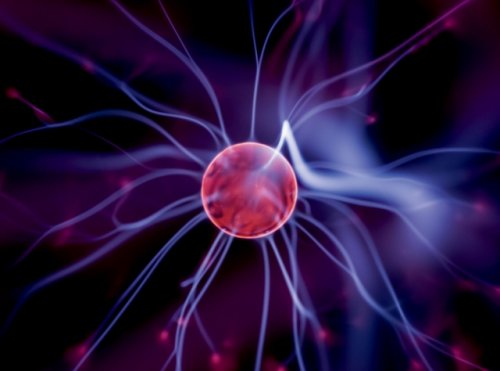
Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.

Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):

1. Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
2. В дальнейшем он вызывает появление магнитного поля.

Уравнения Максвелла в дифференциальной форме

Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.

Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.

Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.

Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.

Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.

Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:

1. Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
2. Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
3. Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.

Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.

Закон Гаусса для магнетизма утверждает (очень кратко):

1. Магнитных монополей не существует.
2. Расхождение полей B или H всегда равно нулю в любом объёме.
3. На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.

Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.

Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.

Уравнения Максвелла в интегральной и дифференциальной форме

Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.

Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.

Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.

Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.

Уравнения Максвелла для электромагнитного поля — основные законы электродинамики

Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.

Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.

Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.

Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).

Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.

Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.

В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.

Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.

Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:

где i, j и k – единичные координатные векторы

Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:

Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.

Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.

Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.

Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.

Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.

Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.

Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.

Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.

Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.

Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.

Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.

Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.

Физический смысл: источником электрического поля является электрический заряд.

Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды:

Линии вектора магнитной индукции В всегда замкнуты.

Уравнения магнитного поля постоянного тока в интегральной форме

В основе расчета магнитного поля постоянных токов лежит следующая система уравнений в интегральной форме:

Эту систему следует дополнить выражением объемной плотности энергии магнитного поля

Первый интеграл известен под названием закона полного тока:

циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов, охватываемых контуром интегрирования.

Как известно, положительными считаются токи, направление которых образует правую винтовую систему с направлением обхода по контуру.

Второй интеграл выражает закон непрерывности магнитного потока:

линии вектора магнитной индукции В всегда замкнуты.

Связь между векторами B и H устанавливается третьим уравнением в котором m магнитная проницаемость вещества, а m₀ магнитная постоянная. Н измеряется в амперах на метр, а В — в веберах на квадратный метр (в теслах). Следует напомнить, что уравнение, (3.3) применимо только для изотропных сред и является частным случаем соотношения, где вектор намагниченности пропорционален напряженности магнитного поля.

Из выражения удельной энергии магнитного поля (3.4) можно получить формулу для силы dFс которой магнитное поле действует на элемент тока Idl

dF=I[Bdl]

Формулу (3.5) часто рассматривают как уравнение, определяющее вектор В.

Уравнения (3.1) — (3.5) являются основой для расчёта магнитных цепей электромеханических устройств, в том числе и электрических машин.

Уравнения магнитного поля постоянного тока в дифференциальной форме

Уравнения поля в дифференциальной форме так же, как и граничные условия, получаются обычно из уравнений поля в интегральной форме путем предельного перехода к бесконечно малым величинам контура и поверхности интегрирования. Применим к элементарному контуру,

ограничивающему площадку DS, через которую проходит ток DIдля точек, где m непрерывно .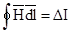

После деления обеих частей этого равенства на DS и перехода к пределу получится

или, учитывая, что проекции векторов равны независимо от
положения контура

.

Это и есть закон полного тока в дифференциальной форме.

Если вихрем вектора напряженности магнитного поля является вектор плотности свободных токов, то вихри вектора магнитной индукции определяются и свободными, и молекулярными токами

.

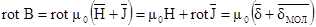
Применение уравнения , (3.9) к поверхности элементарной призмы объема DVприводит к выражению

.

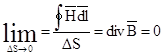
Это и есть закон непрерывности линий магнитной индукции в дифференциальной форме.Этот закон свидетельствует о чисто соленоидальном характере поля вектора В: не существует магнитных зарядов, которые служили бы началами и концами для линий магнитной индукции.

Иначе обстоит дело с вектором H. Из выражения

,

т.е. концы и начала линий вектора намагниченности являются началами и концами линий H. Так, например линии J начинаются на южном полюсе постоянного магнита и, не выходя за пределы магнита, заканчиваются на северном полюсе. Это и дает повод говорить об имеющих чисто расчетный смысл истоках и стоках вектора H как о “положительных магнитных массах” северного полюса, откуда линии Ннаправляются вне и внутри магнита к “отрицательным магнитным массам” южного полюса; так как внутри магнита линия H направлены против В, то принято говорить также о размагничивающем действии полюсов.

Граничные условия для векторов магнитного поля

Для точек, лежащих на поверхности раздела двух сред с различными значениями m, уравнения (3.1) и (3.2) при предельном переходе приводят к граничным условиям. Применим закон полного тока (2.1) к контуру элементарного прямоугольника (аналогичного изображенному на рис. 1.3), у которого основание — бесконечно малая первого порядка, высота—бесконечно малая второго порядка, а площадь, следовательно, бесконечно малая третьего порядка. Циркуляция вектора Н сведется к сумме двух слагаемых:

,

а полный ток, равный произведению средней плотности тока (конечной величины) на площадь прямоугольника,— к нулю. Таким образом, искомое граничное условие получается в виде

.

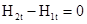
Если же применить закон непрерывности магнитного потока (3.2) к поверхности элементарной призмы (аналогичной изображенной на рис. 1.2), у которой площадь боковых граней бесконечно мала по сравнению с площадью оснований, то нетрудно получить граничное условие для нормальных составляющих вёкторов В_1n и В_2n:

Таким образом, в магнитном поле постоянных токов непрерывны, тангенциальные составляющие векторов Н и нормальные составляющие векторов В. Разумеется, Н и Вна границе сред с разными m меняются скачком, чем и обусловлено преломление магнитных линий.

Вектор-потенциал магнитного поля

Пуcть сформулирована следующая задача требуется рассчитать магнитное поле в однородной среде (m), если задано распределение плотности тока 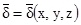, иначе говоря, требуется решить систему уравнений ‘

если плотность тока d задана в виде произвольной функции координат.

Введем новую векторную функцию А =А (х, у, z),позволяющую исключить неизвестные векторы Ви Низ уравнений (3.16) и получить взамен их дифференциальное уравнение, решение которого известно.

Такой подстановкой являетcя уравнение

удовлетворяющее требованию div B=0, так как дивергенция ротора тождественно равна нулю. Теперь можно исключить H из первого уравнения (3.16): _

Учитывая, что m = сопst; и что
получаем

В полученном уравнении можно произвольно задаться значением 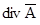, не нарушая уравнения.

Действительно, если изменять величину дивергенции вектора, то будет меняться только величина потенциальной составляющей этого вектора, ротор от которой равен нулю. В рассматриваемом случае проще всего принять

В результате получается векторное уравнение Пуассона
,
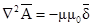
а для точек, где d = 0 —векторное уравнение Лапласа

.

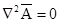
Каждое из этих векторных уравнений распадается на три скалярных уравнения:

Таким образом, определив А из уравнений (3.22) можно определить магнитную индукцию дифференцированием

Векторная функция A, с помощью которой решена поставленная задача, называется векторным потенциалом магнитного поля

Если среда состоит из различныхкусочно-однородных (в магнитном отношении областей” то решение системы (3.22) имеет свои особенности, поскольку в этом случае каждая область описывается своим вектор-потенциалом, который надо находить из уравнения Лапласа (если в области нет токов) либо из уравнения Пуассона. Отдельные решения должны удовлетворять граничным условиям (3.14 ) и (3.15).

Заметим, что граничное условие (3. 14) В_1n=B_2n удовлетворяется, если A1t=A2t. (это требование достаточное, но не необходнмое). Действительно, нормальная составляющая вектора В есть одновременно нормальная составляющая ротора А.Ноиз структуры дифференциального оператора rot A следует_, что его нормальная к поверхности S составляющая определяется изменением вдоль этой поверхности касательных составляющих вектора А. Поэтому, если эти составляющие будут непрерывны, то непрерывны будут также нормальные составляющие rot A и B. В дальнейшем предполагается непрерывность тангенциальных составляющих вектор — потенциала.