§25. Ток смещения и система уравнений Максвелла
Мы установили, что изменяющееся магнитное поле порождает изменяющееся электрическое поле, которое в свою очередь порождает изменяющееся магнитное поле и т. д. В результате образуются сцепленные между собой электрическое и магнитное поля, составляющие электромагнитную волну. Она “отрывается” от зарядов и токов, которые ее породили. Способ существования электромагнитной волны делает невозможным ее неподвижность в пространстве и постоянство напряженности во времени.
Постоянный ток не протекает в цепи с конденсатором, а в случае переменного напряжения в цепи ток протекает через конденсатор. Для постоянного тока конденсатор – разрыв в цепи, а для переменного этого разрыва нет. Поэтому необходимо заключить, что между обкладками конденсатора происходит некоторый процесс, который как бы замыкает ток проводимости. Этот процесс между обкладками конденсатора был назван током смещения. Напряженность поля между обкладками конденсатора 




А значит процессом, замыкающим ток проводимости в цепи, является изменение электрического смещения во времени. Плотность тока

Существование тока смещения было постулировано Максвеллом в 1864 г. и затем экспериментально подтверждено другими учеными.
Почему скорость изменения вектора смещения называется плотностью тока? Само по себе математическое равенство величины 


Уравнение Максвелла с током смещения.
Порождение магнитного поля токами проводимости описывается уравнением

Учитывая порождение поля током смещения, необходимо обобщить это уравнение в виде

Тогда, принимая во внимание (25.2), окончательно получаем уравнение

Являющееся одним из уравнений Максвелла.
Система уравнений Максвелла.
Полученная в результате обобщения экспериментальных данных, эта система имеет вид:

Эти уравнения называются полевыми и справедливы при описании всех макроскопических электромагнитных явлений. Учет свойств среды достигается уравнениями

Называемыми обычно Материальными уравнениями среды. Среды линейны, если 

Рассмотрим физический смысл уравнений.
Уравнение I выражает закон, по которому магнитное поле порождается токами проводимости и смещения, являющимися двумя возможными источниками магнитного поля. Уравнение II выражает закон электромагнитной индукции и указывает на изменяющееся магнитное поле как на один из возможных источников, порождающих электрическое поле. Вторым источником электрического поля являются электрические заряды (уравнение IV). Уравнение III говорит о том, что в природе нет магнитных зарядов.
Полнота и совместность системы. Единственность решения.
В случае линейной среды можно исключить из полевых уравнений (25.6) величины 


Чтобы в этом убедиться возьмем 

Т. е. получили одинаковые дифференциальные следствия. Аналогично возьмем 

С из уравнения непрерывности 



Наличие двух дифференциальных связей и делает систему уравнений Максвелла совместной. Более подробный анализ показывает, что система является полной, а ее решение однозначно при заданных начальных и граничных условиях.
Доказательство единственности решения в общих чертах сводится к следующему. Если имеется два различных решения, то их разность вследствие линейности системы тоже является решением, но при нулевых зарядах и токах и нулевых начальных и граничных условиях. Отсюда, пользуясь выражением для энергии электромагнитного поля и законом сохранения энергии заключаем, что разность решений тождественно равна нулю, т. е. решения одинаковы. Тем самым единственность решения уравнений Максвелла доказана.
Уравнения Максвелла
Вы будете перенаправлены на Автор24
Значение уравнений Максвелла
Уравнения Дж. Максвелла создают основу для предложенной им теории электромагнитных явлений, которая объяснила все известные в то время эмпирические факты, некоторые эффекты предсказала. Главным выводом теории Максвелла стало положение о существовании электромагнитных волн, которые распространяются со скоростью света.
Уравнения, предложенные Максвеллом, в электромагнетизме играют роль подобную роли законов Ньютона в классической механике. Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.
Сам Максвелл предложил двадцать уравнений в дифференциальной форме с двадцатью неизвестными величинами. В современном виде мы имеем систему уравнений Максвелла благодаря немецкому физику Г. Герцу и англичанину О. Хэвисайду. С помощью этих уравнений можно описать все электромагнитные явления.
Система уравнений Максвелла
Систему уравнений Максвелла составляют:
Выражения (1)-(4) называют полевыми уравнениями, они применимы для описания всех макроскопических электромагнитных явлений. Иногда уравнения системы Максвелла группируют в пары, первую пару составляют из второго и третьего уравнения, вторую пару — из первого и четвертого уравнений. При этом говорят, что в первую пару уравнений входят только основные характеристики поля ($\overrightarrow
Каждое из векторных уравнений (1) и (2) эквивалентно трем скалярным уравнениям. Эти уравнения связывают компоненты векторов, которые находятся в левой и правой частях выражений. Так, в скалярном виде уравнение (1) представляется как:
Готовые работы на аналогичную тему
В скалярном виде уравнение (2) запишем как:
Третье уравнение из системы Максвелла в скалярном виде:
Четвертое уравнение в скалярной форме примет следующий вид:
Для того чтобы рассмотреть конкретную ситуацию, систему уравнений (1)-(4) дополняют следующими материальными уравнениями, которые учитывают электромагнитные свойства среды:
Необходимо отметить, что существует целый ряд явлений, в которых материальные уравнения существенно отличны от уравнений (5), например, если речь идет о нелинейных явлениях. В таких случаях получение материальных уравнений составляет отдельную научную задачу.
Физический смысл уравнений Максвелла
Уравнение (1) системы указывает на то, что двумя возможными источниками магнитного поля являются токи проводимости ($\overrightarrow
Уравнение (2) является законом электромагнитной индукции и отображает тот факт, что переменное магнитное поле — один из источников возникновения электрического поля.
Следующим источником электрического поля служат электрические заряды, что и отображает уравнение (4), которое является, по сути, законом Кулона.
Уравнение (3) означает, что линии магнитной индукции не имеют источников (они либо замкнуты, либо уходят в бесконечность), что приводит к выводу об отсутствии магнитных зарядов, которые создают магнитное поле.
Материальные уравнения (5) — это соотношения между векторами поля и токами. Диэлектрические свойства среды заключены в диэлектрической проницаемости ($\varepsilon $). Магнитные свойства, которые описывает намагниченность, учтены в магнитной проницаемости ($\mu $). Проводящие свойства среды сосредоточены в удельной проводимости ($\sigma $).
Уравнения поля линейны и учитывают принцип суперпозиции.
Границы применимости уравнений Максвелла
Система уравнений Максвелла ограничена следующими условиями:
Материальные тела должны быть неподвижны в поле.
Постоянные $\varepsilon ,\ \mu ,\sigma $ могут зависеть от координат, но не должны зависеть от времени и векторов поля.
В поле не должно находиться постоянных магнитов и ферромагнитных тел.
Если существует необходимость учета движения среды, то уравнения системы Максвелла оставляют неизменными, а движение учитывается в материальных уравнениях, которые становятся зависимыми от скорости среды и существенно усложняются. Кроме прочего материальные уравнения перестают быть соотношениями между парами величин, как в (5). Например, плотность тока проводимости становится зависимой от индукции магнитного поля, а не только от напряженности электрического поля.
Магнитное поле постоянных магнитов, например, можно описать, используя систему Максвелла, если известна намагниченность. Но, если заданы токи, то в присутствии ферромагнетиков описать поле при помощи данных уравнений не получится.
Задание: Докажите, что из уравнений Максвелла следует закон сохранения заряда.
Решение:
В качестве основания для решения задачи используем из системы Максвелла уравнение:
Проведем операцию дивергирования в обеих частях выражения (1.1):
Для выражения (1.2) в соответствии с теоремой равенстве нулю дивергенции ротора имеем:
Рассмотрим второе слагаемое в правой части. Мы можем поменять порядок дифференцирования, так как время и пространственные координаты независимы, то есть записать:
В соответствии с системой Максвелла мы знаем, что источниками электрических полей служат заряды или:
Что позволяет нам записать уравнение (1.4) в виде:
Что дает нам закон сохранения заряда, который записан в виде:
Данное уравнение называют уравнением непрерывности тока, оно содержит в себе закон сохранения заряда, что совершенно очевидно, если выражение (1.8), записать в интегральной форме:
тогда если области замкнуты и изолированы получаем:
Что требовалось доказать.
Задание: Покажите, что уравнения $rot\overrightarrow
Решение:
За основу решения примем уравнение:
Возьмём дивергенцию от обеих частей уравнения:
В соответствии с теоремой равенстве нулю дивергенции ротора имеем:
Соответственно, получаем, что
Выражение $div\overrightarrow=const$ не противоречит тому, что $div\overrightarrow=0$.
Мы получили, что уравнения $rot\overrightarrow
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 01 03 2021
Уравнения Максвелла и их физический смысл
Все электромагнитные процессы макроскопической электродинамики подчиняются уравнениям Максвелла, сформулированным в 1873 г. в виде дифференциальных уравнений. Эти уравнения связывают воедино электрические и магнитные характеристики поля:
rot H = Iпр + 

rot Е = — 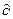

div D = 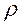
Физический смысл этих уравнений заключается в следующем.
Первое уравнение Максвелла(5.9,а) является обобщенным законом Ампера (закон полного тока) и говорит о том, что если в некоторой точке пространства существует переменное электрическое поле Е, создающее токи проводимости Iпр = σE и токи смещения Iсм = iω 
Второе уравнение Максвелла (5.9,б) является обобщенным законом магнитной индукции Фарадея. Фарадей установил, что если замкнутый контур пронизывается переменным магнитным потоком Ф, то в контуре возникает электродвижущая сила (ЭДС) равная скорости изменения магнитного потока:
е = — 

Знак «минус» в правой части означает, что возникающая в контуре ЭДС стремится воспрепятствовать изменению потока, пронизывающего контур.
Физический смысл второго уравнения Максвелла заключается в том, что всякое изменение магнитного поля во времени непрерывно вызывает независимо от параметров среды появление электрического поля.
Второе уравнение Максвелла связано с гармоническим колебанием соотношением:
rot Е = — 

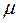
т.е. оно утверждает, что если в некоторой точке пространства существует переменное магнитное поле, то в окрестностях этой точки возникает переменное вихревое электрическое поле. Магнитное поле и создаваемое им электрическое поле образуют левовинтовую систему.
Следует отметить, что электрическое поле может быть как вихревым, так и потенциальным. Источником потенциального электрического поля являются заряды (в случае электрических полей), которые находятся в тех точках пространства, где текут токи проводимости, представляющие собой движущиеся заряды.
Таким образом, гармоническое электрическое поле может быть вихревым, потенциальным или представлять суперпозицию (сумму) потенциального и вихревого полей, тогда как магнитное поле только вихревое.
Первое и второе уравнения Максвелла говорят о том, что между электрической и магнитной составляющими в переменном электромагнитном поле существует тесная взаимосвязь, которая выражается тем, что созданное сторонними источниками меняющееся во времени электромагнитное поле, может существовать вне этого источника за счет собственной энергии, перекачивающейся из энергии электрического поля в энергию магнитного поля и обратно.
Третье уравнение Максвелла(материальное уравнение 5.9,в) — это обобщенный закон Гаусса для случая переменных процессов, физически означает, что источником электрического поля являются электрические заряды, т.е. электрическая индукция D связана с плотностью электрических зарядов 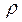
Четвертое уравнениеМаксвелла (материальное уравнение 5.9,г) показывает, что в природе отсутствуют магнитные заряды, а линии вектора В непрерывны и всегда пронизывают любую замкнутую поверхность.
Таким образом, третье и четвертое уравнения Максвелла учитывают электрическую и магнитную характеристики среды. Действительно, в случае линейных изотропных сред можно записать:
D = 
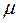
Следует отметить, что к основным уравнениям электродинамики относят и закон Ома в дифференциальной форме (5.6), который выражает зависимость плотности тока Iпр в какой-либо точке проводящей сферы от напряженности электрического поля в этой точке.
Таким образом, мы рассмотрели основные уравнения электродинамики, каждое из которых описывает те или иные свойства электромагнитного поля. Однако, для полного анализа электродинамических процессов необходимо использовать полную систему уравнений Максвелла, содержащую основные уравнения Максвелла (5.9,а-г) и материальные уравнения (5.6) и (5.10), которая записывается в виде:
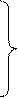



rot Е = — 

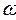
div D = 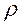
D = 
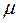
Поскольку уравнения (5.13) и (5.14) являются линейными дифференциальными уравнениями, можно утверждать, что электромагнитные поля удовлетворяют принципу суперпозиции.
http://spravochnick.ru/fizika/uravneniya_maksvella/
http://helpiks.org/4-68998.html

