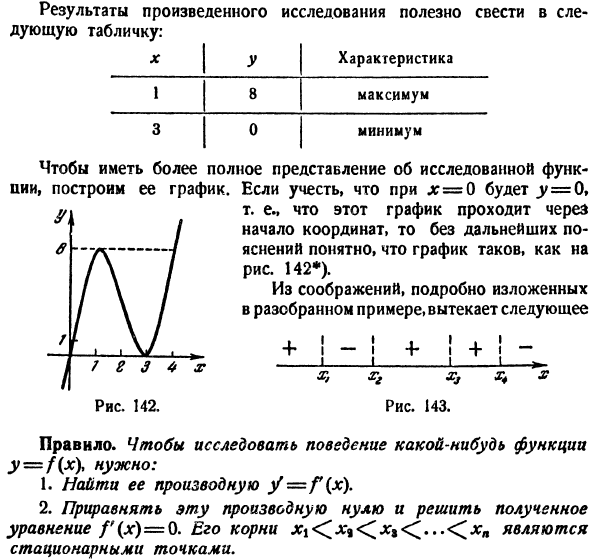
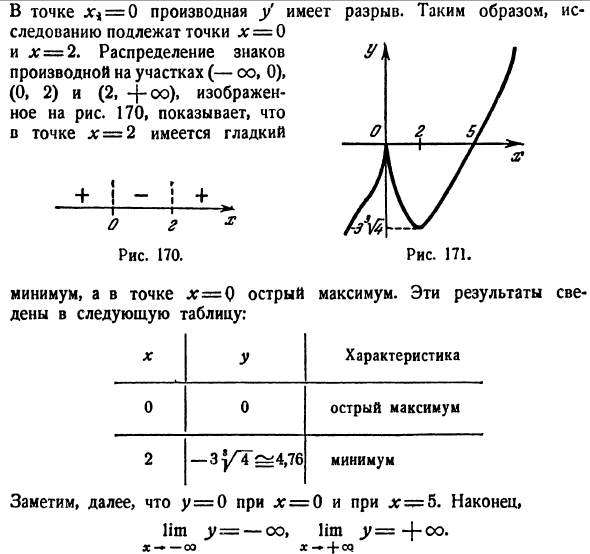
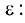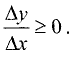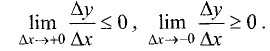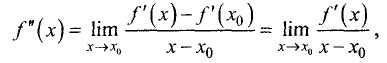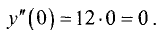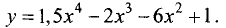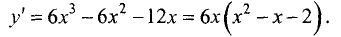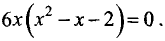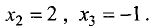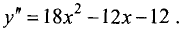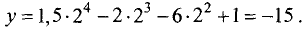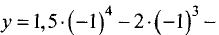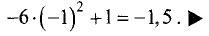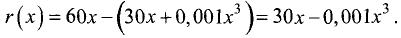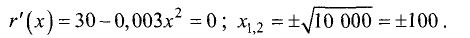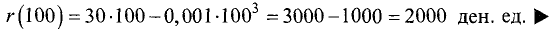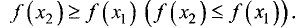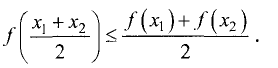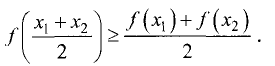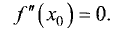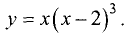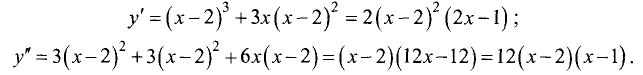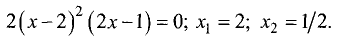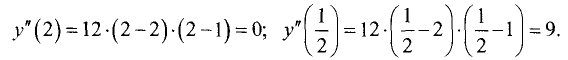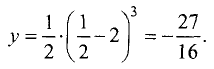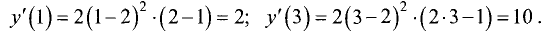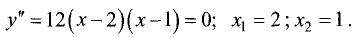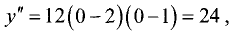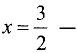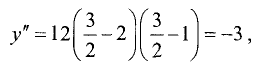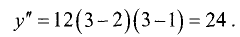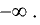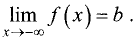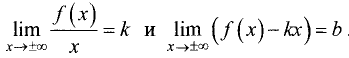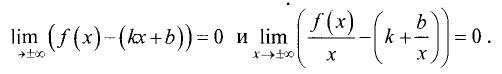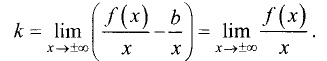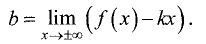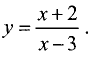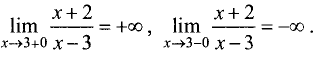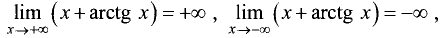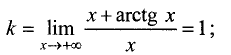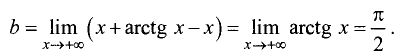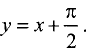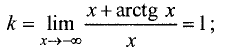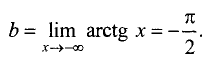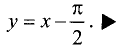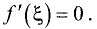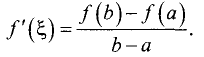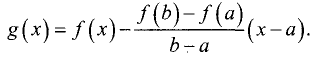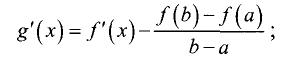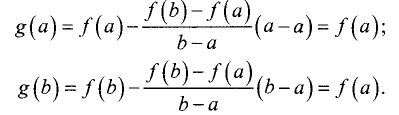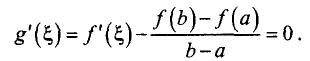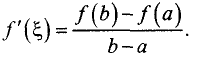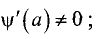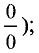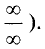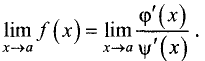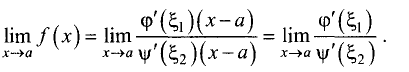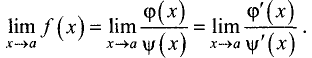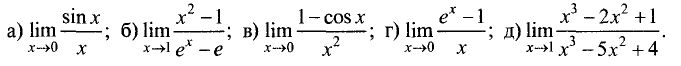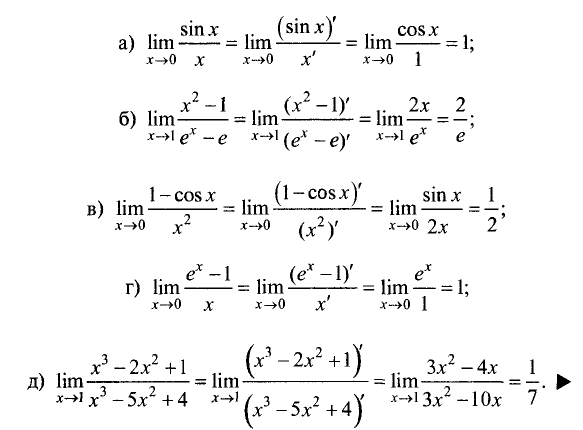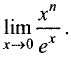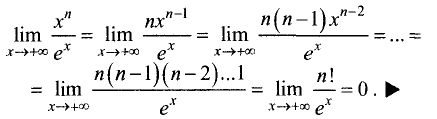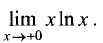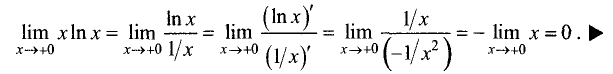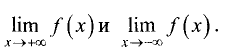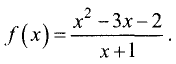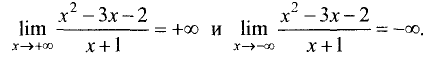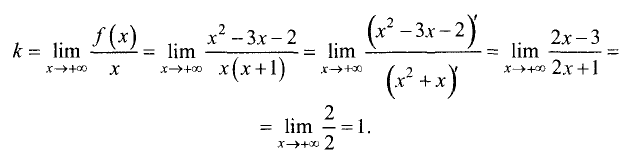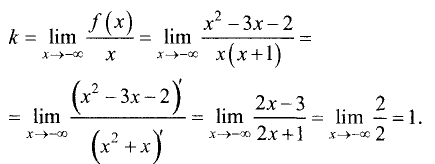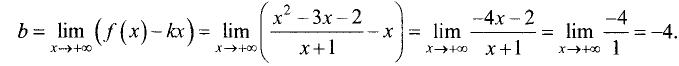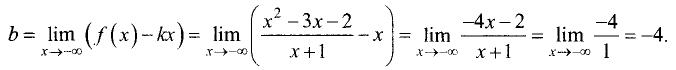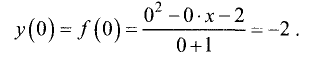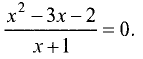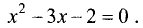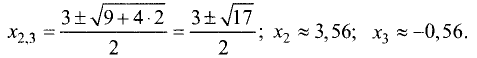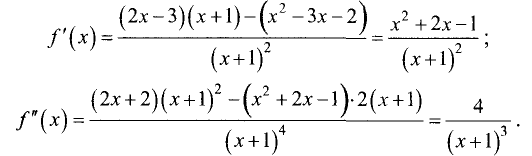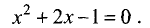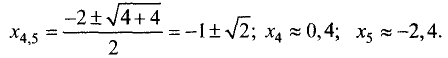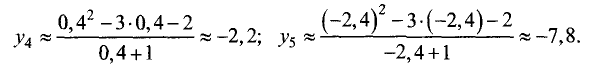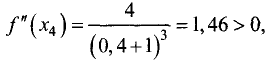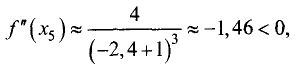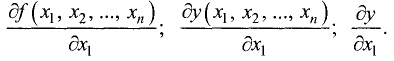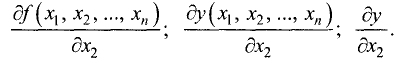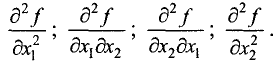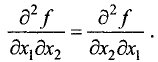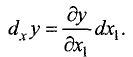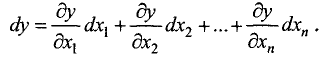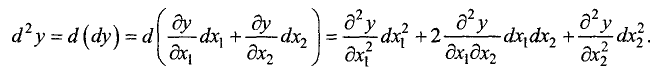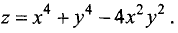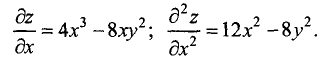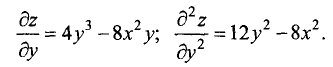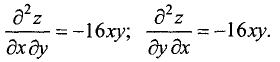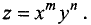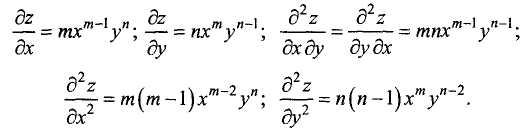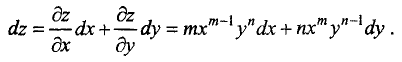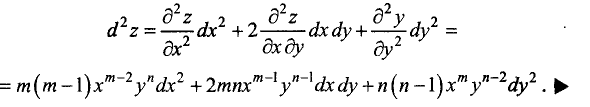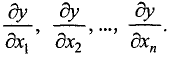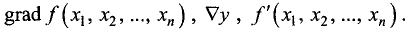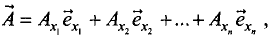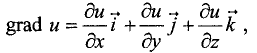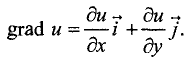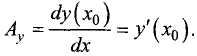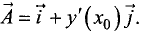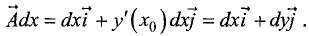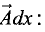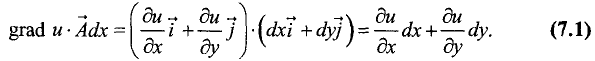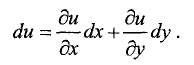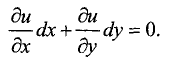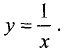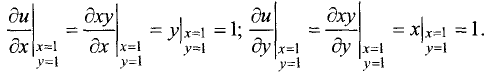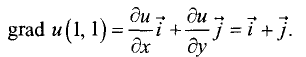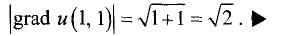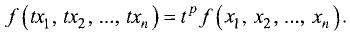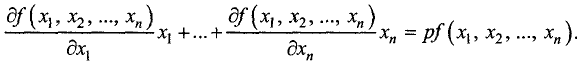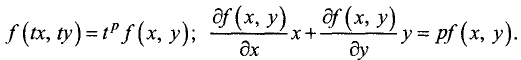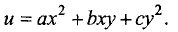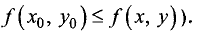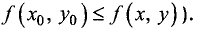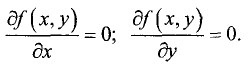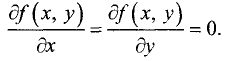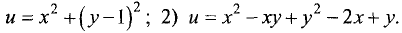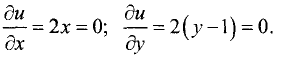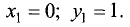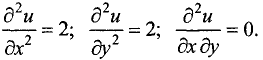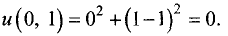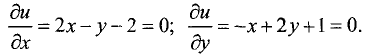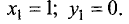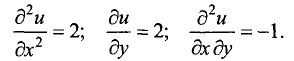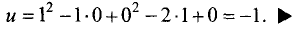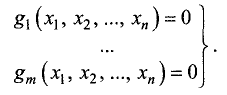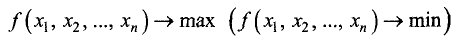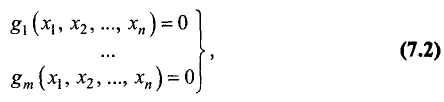Экстремумы функции
Необходимое условие экстремума функции одной переменной
Достаточное условие экстремума функции одной переменной
Если в точке x * выполняется условие:
Пример №1 . Найти наибольшее и наименьшее значения функции: 
Решение.
Критическая точка одна x1 = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
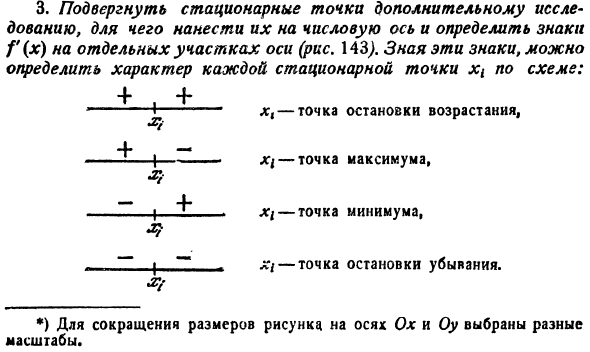
f(1)=9, f(2)= 5 /2, f(3)=3 8 /81
Ответ: fmin= 5 /2 при x=2; fmax=9 при x=1
Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /3+2πk, k∈Z. Находим y’’=2sin(x), вычисляем 

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
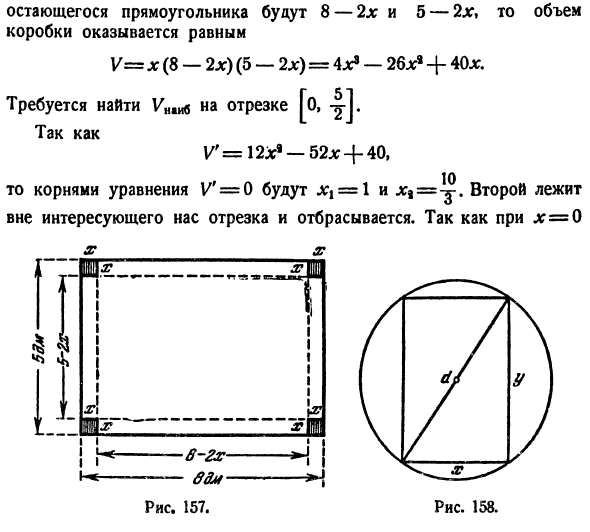
Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x 2
Экстремумы функции: признаки существования, примеры решений
Экстремумы функции, их необходимый и достаточный признаки
Точка экстремума функции — это точка области определения функции, в которой значение функции принимает минимальное или максимальное значение. Значения функции в этих точках называются экстремумами (минимумом и максимумом) функции.
Нахождение эктремумов функции может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графиков. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций. И ещё потребуются таблица производных простых функций и таблица производных сложных функций (откроются в новом окне), так как в примерах указано, какая именно табличная производная найдена.
Рассмотрим график непрерывной функции (рисунок снизу).
Определение. Точка x 1 области определения функции f(x) называется точкой максимума функции, если значение функции в этой точке больше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f(x 0 ) > f(x 0 + Δx) ). В этом случае говорят, что функция имеет в точке x 1 максимум.
Определение. Точка x 2 области определения функции f(x) называется точкой минимума функции, если значение функции в этой точке меньше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f(x 0 ) 0 + Δx) ). В этом случае говорят, что функция имеет в точке x 2 минимум.
Допустим, точка x 1 — точка максимума функции f(x) . Тогда в интервале до x 1 функция возрастает, поэтому производная функции больше нуля ( f ‘(x) > 0 ), а в интервале после x 1 функция убывает, следовательно, и производная функции меньше нуля ( f ‘(x) ). Тогда в точке x 1 производная функции равна нулю или не существует.
Допустим также, что точка x 2 — точка минимума функции f(x) . Тогда в интервале до x 2 функция убывает, а производная функции меньше нуля ( f ‘(x) ), а в интервале после x 2 функция возрастает, а производная функции больше нуля ( f ‘(x) > 0 ). В этом случае также в точке x 2 производная функции равна нулю или не существует.
Теорема Ферма (необходимый признак существования экстремума функции). Если точка x 0 — точка экстремума функции f(x) , то в этой точке производная функции равна нулю ( f ‘(x) = 0 ) или не существует.
Определение. Точки, в которых производная функции равна нулю или не существует, называются критическими точками.
Пример 1. Рассмотрим функцию 
В точке x = 0 производная функции равна нулю, следовательно, точка x = 0 является критической точкой. Однако, как видно на графике функции, она возрастает во всей области определения, поэтому точка x = 0 не является точкой экстремума этой функции.
Таким образом, условия о том, что производная функции в точке равна нулю или не существует, являются необходимыми условиями экстремума, но не достаточными, поскольку можно привести и другие примеры функций, для которых эти условия выполняются, но экстремума в соответствующей точке функция не имеет. Поэтому нужно располагать достаточными признаками, позволяющими судить, имеется ли в конкретной критической точке экстремум и какой именно — максимум или минимум.
Теорема (первый достаточный признак существования экстремума функции). Критическая точка x 0 является точкой экстремума функции f(x) , если при переходе через эту точку производная функции меняет знак, причём, если знак меняется с «плюса» на «минус», то точкой максимума, а если с «минуса» на «плюс», то точкой минимума.
Если же вблизи точки x 0 , слева и справа от неё, производная сохраняет знак, то это означает, что функция либо только убывает, либо только возрастает в некоторой окрестности точки x 0 . В этом случае в точке x 0 экстремума нет.
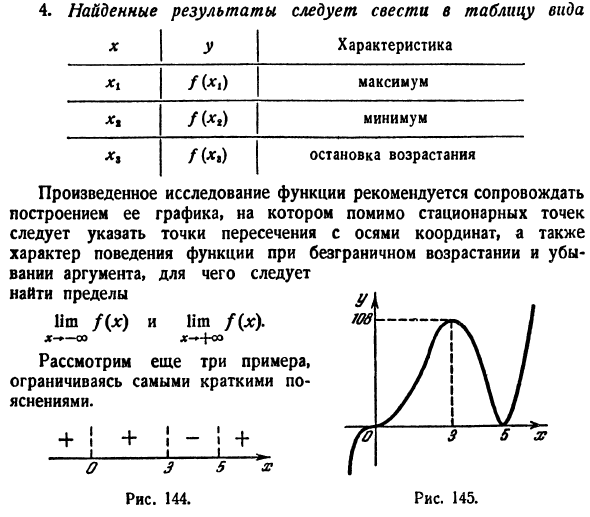
Итак, чтобы определить точки экстремума функции, требуется выполнить следующее:
- Найти производную функции.
- Приравнять производную нулю и определить критические точки.
- Мысленно или на бумаге отметить критические точки на числовой оси и определить знаки производной функции в полученных интервалах. Если знак производной меняется с «плюса» на «минус», то критическая точка является точкой максимума, а если с «минуса» на «плюс», то точкой минимума.
- Вычислить значение функции в точках экстремума.
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Пример 2. Найти экстремумы функции 
Решение. Найдём производную функции (в таблице производных сложных функций — производная 6):

Приравняем производную нулю, чтобы найти критические точки:

Так как для любых значений «икса» знаменатель не равен нулю, то приравняем нулю числитель:

Получили одну критическую точку x = 3 . Определим знак производной в интервалах, разграниченных этой точкой:
в интервале от минус бесконечности до 3 — знак минус, то есть функция убывает,
в интервале от 3 до плюс бесконечности — знак плюс, то есть функция возрастает.
То есть, точка x = 3 является точкой минимума.
Найдём значение функции в точке минимума:

Таким образом, точка экстремума функции найдена: (3; 0) , причём она является точкой минимума.
Теорема (второй достаточный признак существования экстремума функции). Критическая точка x 0 является точкой экстремума функции f(x) , если вторая производная функции в этой точке не равна нулю ( f »(x) ≠ 0 ), причём, если вторая производная больше нуля ( f »(x) > 0 ), то точкой максимума, а если вторая производная меньше нуля ( f »(x) ), то точкой минимума.
Замечание 1. Если в точке x 0 обращаются в нуль и первая, и вторая производные, то в этой точке нельзя судить о наличии экстремума на основании второго достаточного признака. В этом случае нужно воспользоваться первым достаточным признаком экстремума функции.
Замечание 2. Второй достаточный признак экстремума функции неприменим и тогда, когда в стационарной точке первая производная не существует (тогда не существует и вторая производная). В этом случае также нужно вопользоваться первым достаточным признаком экстремума функции.
Локальный характер экстремумов функции
Из приведённых определений следует, что экстремум функции имеет локальный характер — это наибольшее и наименьшее значение функции по сравнению с близлежайшими значениями.
Предположим, вы рассматриваете свои заработки в отрезке времени протяжённостью в один год. Если в мае вы заработали 45 000 рублей, а в апреле 42 000 рублей и в июне 39 000 рублей, то майский заработок — максимум функции заработка по сравнению с близлежайшими значениями. Но в октябре вы заработали 71 000 рублей, в сентябре 75 000 рублей, а в ноябре 74 000 рублей, поэтому октябрьский заработок — минимум функции заработка по сравнению с близлежашими значениями. И вы легко видите, что максимум среди значений апреля-мая-июня меньше минимума сентября-октября-ноября.
Говоря обобщённо, на промежутке функция может иметь несколько экстремумов, причём может оказаться, что какой-либо минимум функции больше какого-либо максимума. Так, для функции изображённой на рисунке выше, 
То есть не следует думать, что максимум и минимум функции являются, соответственно, её наибольшим и наименьшим значениями на всём рассматриваемом отрезке. В точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума, а в точке минимума — наименьшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке минимума.
Поэтому можно уточнить приведённое выше понятие точек экстремума функции и называть точки минимума точками локального минимума, а точки максимума — точками локального максимума.
Ищем экстремумы функции вместе
Пример 3. Найти экстремумы функции 
Решение. Функция определена и непрерывна на всей числовой прямой. Её производная (и первое, и второе слагаемые — табличная производная 3) 







Для интервала 




















Чтобы уточнить построение графика, найдём точки пересечения его с осями координат. При 



Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Пример 4. Найти экстремумы функции 
Областью определения функции является вся числовая прямая, кроме точки 

Для сокращения исследования можно воспользоваться тем, что данная функция чётная, так как 

Находим производную (каждое слагаемое находим как табличную производную 3) 
1) 
2) 
но функция терпит разрыв в этой точке, поэтому она не может быть точкой экстремума.
Таким образом, заданная функция имеет две критические точки: 









Чтобы составить более полное представление о графике функции, выясним её поведение на границах области определения:
(здесь символом 




т.е. если 

Точек пересечения с осями график функции не имеет. Рисунок — в начале примера.
Найти экстремумы функции самостоятельно, а затем посмотреть решение
Пример 5. Найти экстремумы функции 
Пример 6. Найти экстремумы функции 
Пример 7. Найти экстремумы функции 
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Продолжаем искать экстремумы функции вместе
Пример 8. Найти экстремумы функции 
Решение. Найдём область определения функции. Так как должно выполняться неравенство 


Найдём первую производную функции (производная вида 2 в таблице производных сложной функции):
Найдём критические точки функции:
Точки 





Найдём значения функции в этих точках:
Таким образом, экстремумы функции:

Пример 9. Найти экстремумы функции 
Решение. Найдём область определения функции.
Найдём критические точки функции:
Таким образом, у данной функции две критические точки: 




Найдём значение функции в точке минимума:
Таким образом, минимум функции:

Пример 10. Найти экстремумы функции 
Решение. Найдём первую производную функции (первое слагаемое — производная вида 12 в таблице производных простых функций, второе — производная вида 6 в таблице производных сложной функции):

Найдём критические точки функции:

Так как для любого действительного x должно выполняться условие 

Таким образом, данная функция имеет одну критическую точку. Определим значения производной в критической точке. При переходе через точку 

Найдём значение функции в точке максимума:

Таким образом, максимум функции:

Исследование функций с примерами решения и образцами выполнения
Исследование функции — задача, заключающаяся в определении основных параметров заданной функции. Одной из целей исследования является построение графика функции.
Точки экстремума
Максимумом или минимумом функции y = f(x) называется
такое ее значение 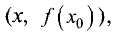
неравенства при любых малых положительных и отрицательных значениях
■ 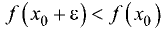
■ 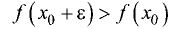
Таким образом, в точках максимума (минимума) значение 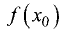
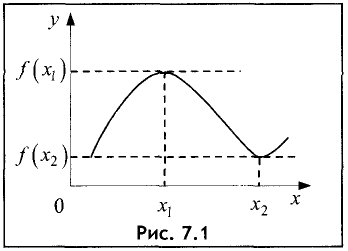
Функция, представленная на рис. 7.1, в точке 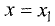
максимум, а в точке 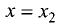
Точки, в которых функция принимает максимальное или минимальное значения, называются точками экстремума.
Необходимое условие максимума и минимума функции
Теорема Ферма:
Если функция определена и дифференцируема
в некотором промежутке X и во внутренней точке этого промежутка 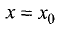
производная функции в этой точке равна нулю, т.е.
Доказательство:
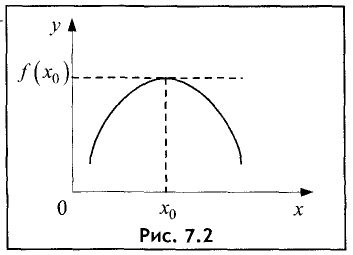
Пусть функция y = f(x) в точке 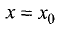
промежутка X имеет наибольшее значение (рис. 7.2).
Тогда 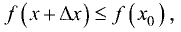
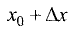
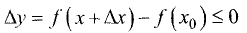
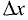
Если 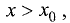
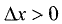
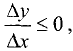
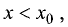
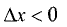
Переходя к пределам справа при 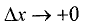
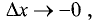
получим
Так как по условию функция y=f(x) дифференцируема в
точке 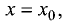
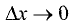
стремления (слева или справа).
т.е. 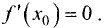
Необходимым условием максимума (минимума) непрерывной функции является равенство нулю первой производной.
Это условие является следствием теоремы Ферма. Действительно, если в точке 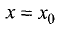
Необходимое условие максимума или минимума непрерывной функции имеет простой геометрический смысл. Так как в экстремальных точках касательная параллельна оси Ох (см. рис. 7.1 и 7.2), т.е. угол наклона касательной к оси Ох равен нулю, то тангенс данного угла, который равен производной, также равен нулю.
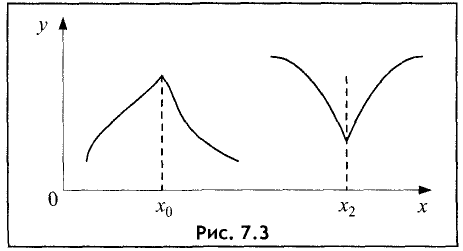
Максимум или минимум может иметь место также в тех точках, где производная не существует вовсе (рис. 7.3).
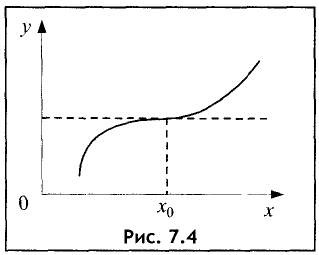
Приведенное условие существования экстремумов является необходимым, но не достаточным. На рис. 7.4 приведен случай, когда необходимое условие выполняется в точке 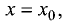
Достаточные условия существования экстремума
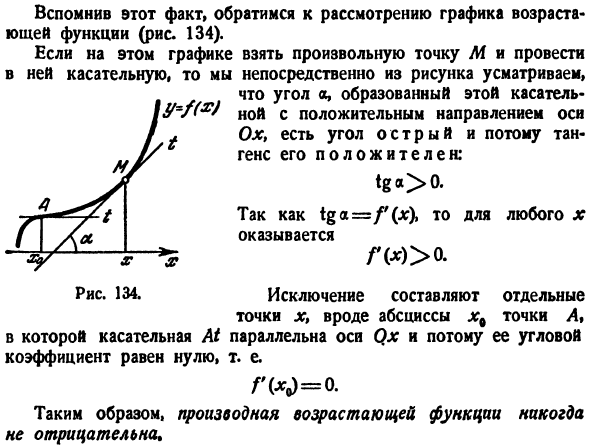
Первое условие. Если при переходе через точку 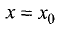
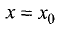
Действительно, если 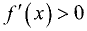
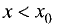
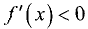
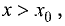
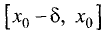
промежутке 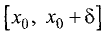
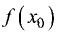
наибольшим в промежутке 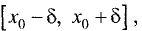
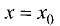
Если при переходе через точку 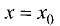
своего знака, то в точке 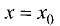
(см. рис. 7.4).
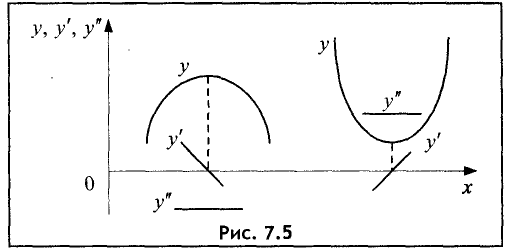
Второе условие. Если функция y = f(x) дважды дифференцируема в точке 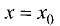
нулю, а вторая производная в этой точке положительна, то точка
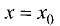
функции y = f(x) отрицательна в точке 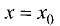
Действительно, вторая производная вычисляется по формуле:
так как 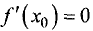
Пусть 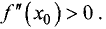
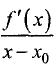
из окрестности точки 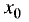
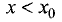
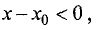
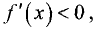
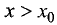
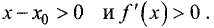
точки 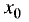
в такой точке имеет место минимум. Аналогично можно показать,
что при 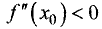
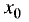
поясняется на рис. 7.5.
Если вторая производная в некоторой точке равна нулю, то эта
точка также может быть экстремальной. Например, для функции
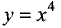
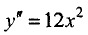
Алгоритм исследования функции на экстремум
1.Найти производную функции и приравнять ее нулю.
2.Решив это уравнение, определить подозрительные точки.
3.Исследовать знак производной слева и справа от каждой
подозрительной точки и принять решение о наличии
минимума или максимума.
4.Найти значения функции в экстремальных точках.
Пример:
Найти максимумы и минимумы функции
Решение:
Область определения функции — вся числовая ось.
Определяем производную:
Подозрительные точки находим, решая уравнение
Отсюда 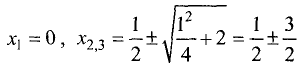
Определяем вторую производную:
Для точки 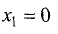
имеет место максимум. Его значение равно
у = 1,5*0-2*0-6*0 + 1 = 1.
Для точки 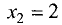
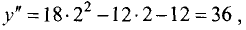
имеет место минимум. Его значение равно
Для точки 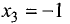
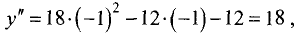
точке имеет место минимум. Его значение равно
Пример:
Производитель реализует свою продукцию по цене
60 ден. ед. за единицу продукции. Издержки производителя
определяются кубической зависимостью 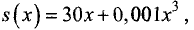
количество изготовленной и реализованной продукции. Найти оптимальный объем выпуска и соответствующий ему доход.
Решение:
Доход определяется разностью между выручкой за
проданную продукцию 60х и ее себестоимостью, т.е.
Для определения оптимального объема выпуска найдем производную
этой функции, приравняем ее нулю и решим полученное уравнение
Отрицательный корень не имеет экономического смысла, поэтому
для дальнейших исследований принимаем 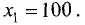
производная в исследуемой точке r»(х) = -0,006х = -0,006 • 100 = -0,6 является отрицательной, т.е. в этой точке имеет место максимум функции. Таким образом, оптимальный объем выпуска равен 100 единицам продукции.
Доход, соответствующий оптимальному выпуску,
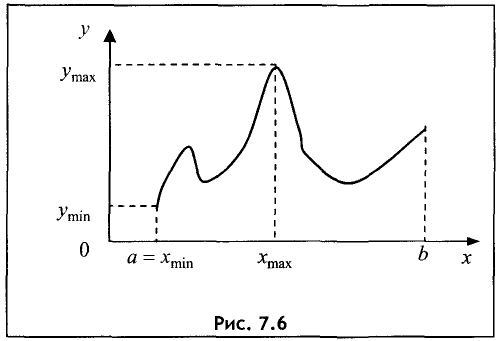
Для определения наибольшего и наименьшего значений на
отрезке, помимо указанного алгоритма, находят значения функции на концах отрезка. Затем выбирают наибольшее и наименьшее
значения из этих двух и всех экстремальных значений. Смысл
сказанного поясняется на рис. 7.6.
Монотонность и выпуклость функций
Функция y = f(x) не убывает (не возрастает) на промежутке X, если для любых 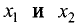
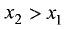
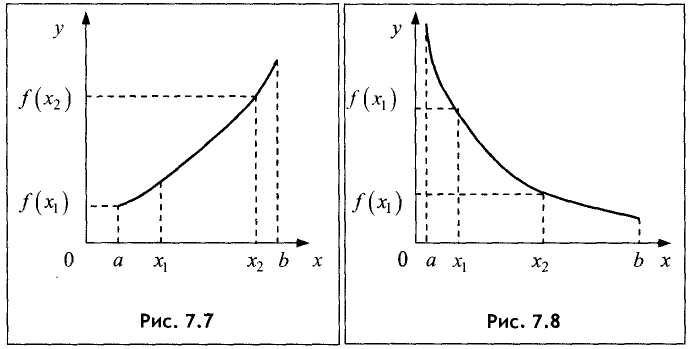
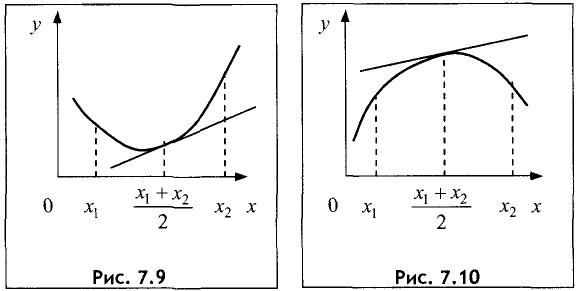
Если меньшему значению неравенства аргумента соответствует меньшее значение функции, то функция называется возрастающей (рис. 7.7). Если меньшему значению аргумента соответствует большее значение функции, то функция называется убывающей (рис.7.8).
Функции возрастающие и убывающие называются монотонными.
Функция называется ограниченной на промежутке X, если существует такое положительное число М > 0, что 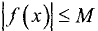
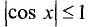
Функция y = f(x) на интервале (а,b) имеет выпуклость вниз (вверх), если в пределах данного интервала график лежит не ниже (не выше) любой касательной к графику функции. На рис. 7.9 изображен график функции, имеющей выпуклость вниз, а на рис. 7.10 — график функции, имеющей выпуклость вверх.
Функция y = f(x) на интервале (а, b) называется выпуклой вниз, если для любых двух значений 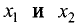
Функция y = f(x) на интервале (а, b) называется выпуклой вверх, если для любых двух значений 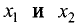
При исследовании функций бывают полезны две следующие
теоремы.
Теорема:
Функция выпукла вниз (вверх) тогда и только тогда,
когда ее первая производная на этом промежутке монотонно
возрастает (убывает).
Теорема:
Если вторая производная дважды дифференцируемой
функции положительна (отрицательна) внутри интервала (a, b), то
функция выпукла вниз (вверх) внутри этого интервала (достаточное
условие).
Однако, данное условие справедливо не всегда. Например,
функция 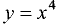
производная 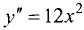
Точка 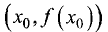
y = f(x), если в этой точке график имеет касательную и существует
такая окрестность точки 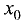
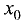
На рис. 7.4 точка 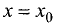
Необходимое условие перегиба. Вторая производная дважды
дифференцируемой функции в точке перегиба 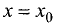
Достаточное условие перегиба. Вторая производная дважды
дифференцируемой функции при переходе точки перегиба 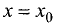
меняет свой знак.
Алгоритм исследования функции на выпуклость и точки перегиба
1.Найти вторую производную функции и приравнять ее нулю.
2.Решив это уравнение, определить подозрительные точки.
3.Исследовать знак второй производной слева и справа от
каждой подозрительной точки и принять решение об интервалах
выпуклости и наличии точек перегиба.
4.Найти значения функции в точках перегиба.
Пример:
Найти экстремальные точки, интервалы выпуклости
и точки перегиба функции
Решение:
Находим первую и вторую производные исследуемой
функции:
Приравняем нулю первую производную и решим полученное
уравнение:
Подставив полученные значения в формулу для второй
производной, найдем
Таким образом, точка 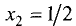
Значение исследуемой функции в этой точке
Точку 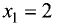
производная определена на всей числовой оси, так как точек, в которых производная отсутствует, не существует. Исследуем знак производной на интервале 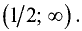
Так как слева и справа от точки 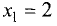
положительный, то в этой точке экстремума нет.
Приравняем нулю вторую производную и решим полученное
уравнение:
Вторая производная также определена на всей числовой оси. В
точке х = 0 значение второй производной
в точке
■ на интервале 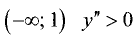
■ на интервале (1; 2) у» Асимптоты функций
Прямая называется асимптотой функции y = f(x), если расстояние от
точки (х, f(x)) , лежащей на графике функции, до этой прямой
стремится к нулю при движении точки по графику в бесконечность.
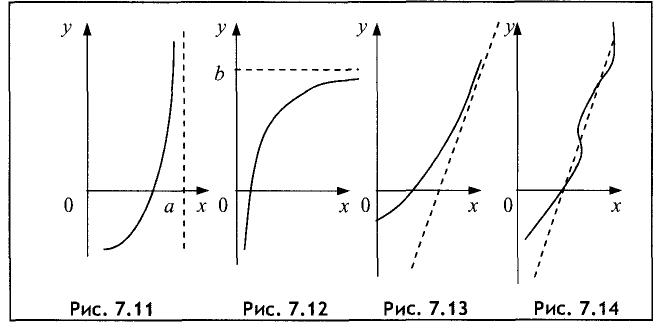
Существуют три вида асимптот: вертикальные (рис. 7.11),
горизонтальные (рис. 7.12) и наклонные (рис. 7.13, 7.14).
На рис. 7.14 кривая приближается к асимптоте, все время пересекая ее.
Прямая х = а называется вертикальной асимптотой графика
функции у = f(x), если хотя бы одно из предельных значений 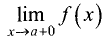
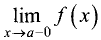
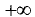
Прямая у = b называется горизонтальной асимптотой графика
функции y = f (х), если 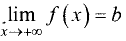
Прямая y = kx + b 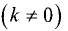
графика функции у = f(x), если существуют конечные пределы
Действительно, если у = kх + b — наклонная асимптота, то
Из последнего выражения следует
При известном k из равенства 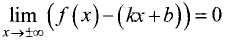
Если для горизонтальной и наклонной асимптот конечен только
предел при 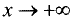
Пример:
Найти асимптоты графика функции
Решение:
Областью определения является вся числовая ось,
кроме точки х = 3 . Причем
Поэтому прямая х = 3 — вертикальная асимптота. Так как 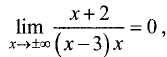
Пример:
Найти асимптоты графика функции у = х + arctg х.
Решение. Функция непрерывна на всей числовой оси, поэтому
вертикальные асимптоты отсутствуют. Так как
то отсутствуют и горизонтальные асимптоты.
Для правосторонней наклонной асимптоты
Уравнение правосторонней асимптоты имеет вид
Для левосторонней наклонной асимптоты
Уравнение правосторонней асимптоты имеет вид
Правило Лопиталя
При отыскании предела часто сталкиваются с
неопределенностями 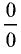
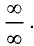
Прежде чем переходить к доказательству правила Лопиталя,
рассмотрим две теоремы.
Теорема Ролля:
Пусть функция y = f(x) удовлетворяет
следующим условиям:
■ непрерывна на промежутке [а,b];
■ дифференцируема на промежутке (а,b);
■ на концах промежутка принимает равные значения, т.е.
f(a) = f(b).
Тогда внутри промежутка существует по крайней мере одна точка
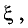
Доказательство. Действительно, если внутри промежутка функция имеет хотя бы одну точку, в которой она принимает наибольшее или наименьшее значение, то в соответствии с теоремой Ферма производная в этой точке равна нулю. Если же таких точек нет, то функция тождественно постоянна на всем интервале. Тогда производная равна нулю во всех точках указанного интервала.
Теорема Лагранжа:
Пусть функция y = f(x) удовлетворяет
следующим условиям:
■ непрерывна на промежутке [а, b];
■ дифференцируема на промежутке (а, b).
Тогда внутри промежутка существует по крайней мере одна точка
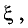
приращения функции на приращение аргумента на данном промежутке:
Доказательство:
Эта функция удовлетворяет условиям теоремы Ролля, поскольку она:
■ непрерывна на промежутке [а, b];
■ дифференцируема на промежутке (а, b) и
■ на концах промежутка принимает равные значения:
Следовательно, внутри промежутка существует по крайней мере одна точка 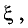
Отсюда находим
Правило Лопиталя
Пусть 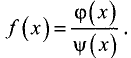
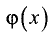
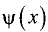
■ непрерывны на промежутке [х, а];
■ дифференцируемы на промежутке (х, а) и
■ 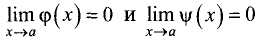
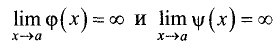
Тогда
Доказательство:
Доказательство проведем для неопределенности 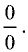
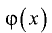
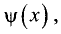
Так как при 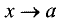
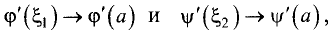
В случае, если 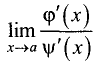
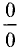
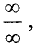
Пример:
Используя правило Лопиталя, найти пределы:
Решение:
Во всех примерах имеем неопределенность 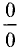
Пример:
Используя правило Лопиталя, найти предел
Решение:
Имеем неопределенность 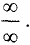
Пример:
Используя правило Лопиталя, найти предел
Решение:
Имеем неопределенность 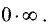
знаменатель на х , получим 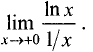
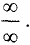
Построение графиков функций
Изучение функции и построение ее графика целесообразно
проводить по следующей схеме:
1.Найти область существования функции, точки разрыва и
определить их характер.
2.Определить поведение функции в бесконечности, вычислив
пределы
4.Найти пересечение кривой с осью Ох, решая уравнение
f(x) = 0, и с осью Оу , вычисляя у = f(0).
5.Найти экстремумы и интервалы монотонности функции.
6.Найти интервалы выпуклости функции и точки перегиба.
7.По полученным данным постепенно делают набросок
кривой, уточняя его по отдельным точкам.
Пример:
Построить график функции
Решение:
1. Эта функция определена и непрерывна для всех 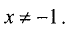
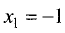
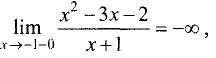
а справа — 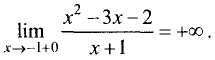
2.Пределы функции в бесконечности:
3.Определим параметры наклонных асимптот. Угловой
коэффициент справа
Угловой коэффициент слева
Точка пересечения асимптоты с осью Оу справа
Точка пересечения асимптоты с осью Оу слева
Таким образом, параметры правой и левой асимптот совпали,
т.е. имеет место одна асимптота, определенная уравнением прямой
у = х-4.
4.Точка пересечения кривой с осью Оу находится из
соотношения
Точка пересечения кривой с осью Ох находится из уравнения
Дробь равна нулю, если числитель равен нулю, т.е.
Решение данного квадратного уравнения имеет вид
5.Для определения экстремумов и интервалов монотонности
функции найдем первую и вторую производные:
Приравняв нулю первую производную, получим:
Решив данное уравнение, найдем подозрительные точки:
Значения функции в этих точках:
Подставив полученные координаты экстремальных точек в формулу
второй производной, найдем:
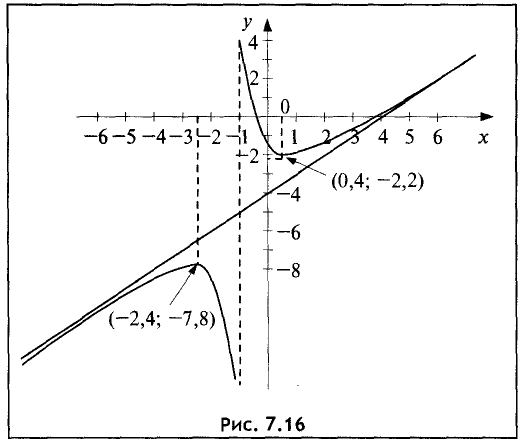
т.е. в точке (0,4; -2,2) имеет место минимум,
т.е. в точке (-2,4; -7,8) имеет место максимум.
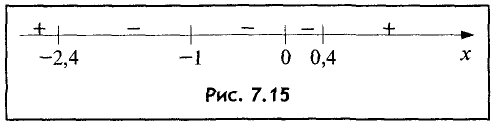
Для исследования функции на монотонность проследим поведение производных внутри полученных интервалов (рис. 7.15). Знаками плюс и минус показан знак производной на данном интервале.
В точке 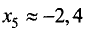
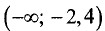
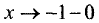
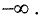
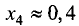
место минимум, поэтому на промежутке (-1; 0,4) функция
убывает, а на промежутке 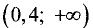
6.Для нахождения точек перегиба приравняем нулю вторую производную: 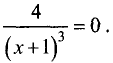
По полученным данным строим график функции (рис. 7.16). ►
Производные и дифференциалы функций нескольких переменных
Пусть задана функция n переменных
Первой частной производной функции 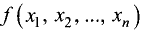
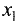
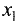
Аналогично определяется первая частная производная по любой другой переменной. Например, первую частную производную по 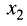
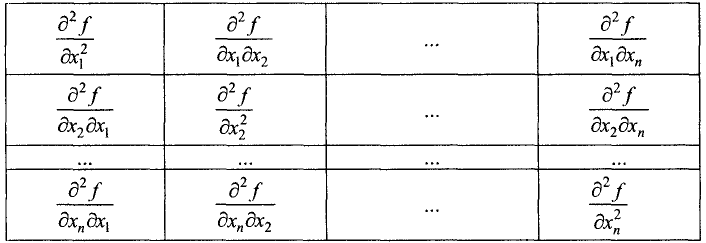
Второй частной производной функции 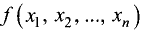
Функция n переменных имеет 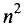
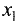
Таблица 7.1
Для функции двух переменных имеем четыре вторые частные производные:
Вторая частная производная по двум различным переменным, например 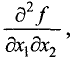
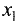
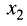
Аналогично определяются производные более высоких порядков, например третья частная производная, четвертая частная производная и т.д.
Частный дифференциал функции n переменных 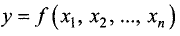
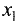
Полный дифференциал функции n переменных 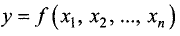
Полный дифференциал второго порядка функции двух переменных 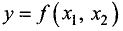
Пример:
Найти частные производные первого и второго порядка от функции
Решение:
Находим первую и вторую частные производные по х:
Находим первую и вторую частные производные по у :
Находим смешанные вторые частные производные:
Как и следовало ожидать, смешанные частные производные равны. ►
Пример:
Найти дифференциалы первого и второго порядков от функции
Решение. Частные производные первого и второго порядков исследуемой функции равны:
Дифференциал первого порядка
Дифференциал второго порядка
Градиент
Градиентом функции n переменных 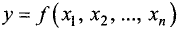
При этом пишут grad y,
Известно, что вектор 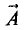
где 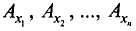
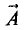
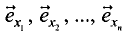
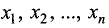
Градиент функции трех переменных u = f(x, у, z) можно представить в виде
где 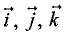
Градиент функции в заданной точке показывает направление самого быстрого роста функции в этой точке.
В экономике достаточно часто используются функции двух переменных. Градиент функции двух переменных u = f(х, у) можно представить в виде
Существует четкая связь между линиями уровня таких функций и направлением градиента.
Теорема:
Пусть задана дифференцируемая функция u = f(x,у) и величина градиента данной функции, отличная от нуля, в точке 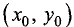
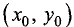
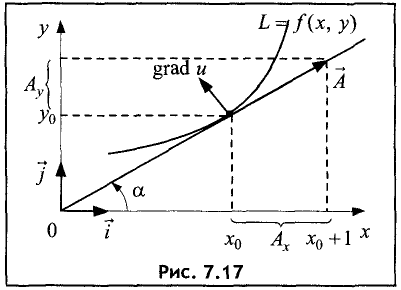
Доказательство. Линия уровня, представленная на рис. 7.17, задана уравнением L = f(x, у).
В точке 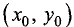
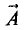
Пусть проекция вектора 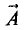
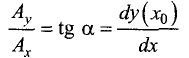
Таким образом, вектор 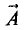
Умножив данный вектор на dx , получим
Найдем скалярное произведение градиента функции u = f(x,y)
в точке 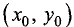
С другой стороны, полный дифференциал функции u = f(x, у)
в точке
На линии уровня функция u = f(x, у) не изменяется по определению, поэтому полный дифференциал по направлению вектора 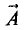
Сопоставив это выражение с (7.1), можно сделать вывод о
перпендикулярности векторов 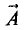
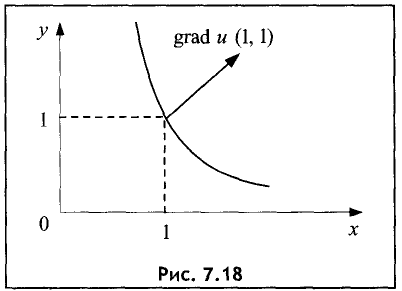
Пример:
Для функции u = ху построить линию уровня, проходящую через точку 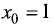
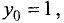
точке.
Решение:
Уровень в исследуемой точке равен с = 1 • 1 = 1. Линия уровня определяется формулой
1 = ху или
Таким образом, линией уровня является гипербола.
Для отыскания градиента найдем частные производные функции в
исследуемой точке:
Отсюда следует выражение для градиента функции в исследуемой
точке:
Из полученной формулы видно, что градиент в исследуемой точке
направлен вправо вверх под углом 45° к осям Ох и Оу (рис. 7.18).
Его модуль равен
Однородные функции
Пусть задана функция и переменных 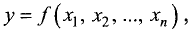
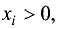
Функция 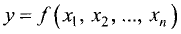
Заметим, что условие определения функции 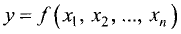
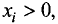
Для однородных функций п переменных 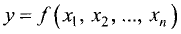
Для однородной функции двух переменных u=f(x, у) степени р имеем
Приведенные формулы называются формулами Эйлера.
Пример:
Определить степень однородных функций:
б)
Решение:
a) a(tx) + b(ty) = t(ax + by) = tu , т.е. функция u = ax + by имеет первую степень однородности;
б) 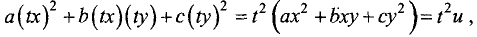
Экстремумы функции двух переменных
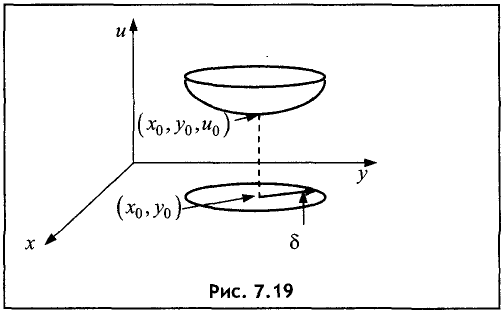
Пусть задана функция двух переменных u = f(x, у).
Точка 

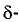

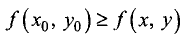
Двумерной 

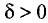

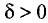
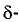



Если 
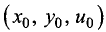
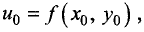
u = f(х,у) имеет вид шапочки, повернутой выпуклостью вверх
(максимум) или вниз (минимум).
Точка 
максимума (глобального (абсолютного) минимума) функции u = f(x,у), если для всех точек (х, у), для которых функция u = f(х, у) определена, справедливо неравенство 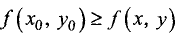
Пусть функция u = f(x, у) определена в окрестности точки

условием локального экстремума данной функции в точке 
является равенство нулю первых частных производных:
Эти точки являются подозрительными и среди них следует
искать точки локального экстремума. Подозрительные точки не
обязаны быть точками локального экстремума.
Достаточное условие локального экстремума функции u = f(x, у)
дважды дифференцируемой в точке 
Пусть функция u = f(x, у) в точке 
производные, равные нулю:
1.Если 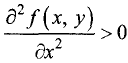
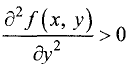
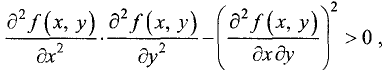

2. Если 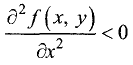
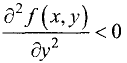
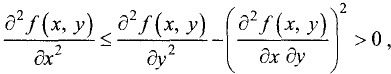

3.Если 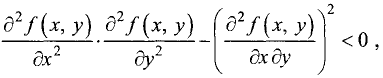

Пример:
Исследовать на экстремум следующие функции
нескольких переменных: 1)
Решение:
1.Находим первые частные производные и приравниваем их к нулю:
Решив полученные уравнения, находим подозрительные точки:
Находим в подозрительной точке вторые частные производные:
Так как 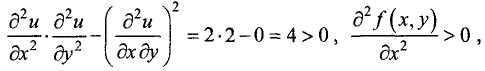
2.Находим первые частные производные и приравниваем их к нулю:
Решив систему из двух уравнений, находим подозрительные точки:
Находим в подозрительной точке вторые частные производные:
Так как 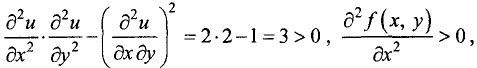
Условный экстремум
При определении безусловного экстремума функции п
независимых переменных 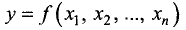
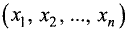
дополнительных условий. В задачах на условный экстремум поведение независимых переменных ограничено определенными условиями. Рассмотрим эту задачу для n независимых переменных в следующей формулировке.
Найти локальный экстремум функции n независимых
переменных 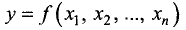
Задача на условный экстремум записывается следующим образом:
где m Дополнение к исследованию функции




































Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://function-x.ru/function_extremum.html
http://lfirmal.com/issledovanie-funkcij/