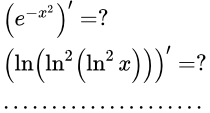Уравнения на производную сложной функции

Сложная функция. Производная сложной функции

Раз ты зашел сюда, то уже, наверное, успел увидеть в учебнике эту формулу

и сделать вот такое лицо:

Друг, не переживай! На самом деле все просто до безобразия. Ты обязательно все поймешь. Только одна просьба – прочитай статью не торопясь, старайся понять каждый шаг. Я писал максимально просто и наглядно, но вникнуть в идею всё равно надо. И обязательно реши задания из статьи.

Что такое сложная функция?

Представь, что ты переезжаешь в другую квартиру и поэтому собираешь вещи в большие коробки. Пусть надо собрать какие-нибудь мелкие предметы, например, школьные письменные принадлежности. Если просто скидать их в огромную коробку, то они затеряются среди других вещей. Чтобы этого избежать, ты сначала кладешь их, например, в пакет, который затем укладываешь в большую коробку, после чего ее запечатываешь. Этот «сложнейший» процесс представлен на схеме ниже:

Казалось бы, причем здесь математика? Да притом, что сложная функция формируется ТОЧНО ТАКИМ ЖЕ способом! Только «упаковываем» мы не тетради и ручки, а \(x\), при этом «пакетами» и «коробками» служат разные функции .

Например, возьмем x и «запакуем» его в функцию косинуса :

В результате получим, ясное дело, \(\cos⁡x\). Это наш «пакет с вещами». А теперь кладем его в «коробку» — запаковываем, например, в кубическую функцию.

Что получится в итоге? Да, верно, будет «пакет с вещами в коробке», то есть «косинус икса в кубе».

Получившаяся конструкция и есть сложная функция. Она отличается от простой тем, что к одному иксу применяется НЕСКОЛЬКО «воздействий» (упаковок) подряд и получается как бы «функция от функции» — «упаковка в упаковке».

В школьном курсе видов этих самых «упаковок» совсем мало, всего четыре :

Давай теперь «упакуем» икс сначала в показательную функцию с основанием 7, а потом в тригонометрическую функцию тангенс . Получим:

А теперь «упакуем» икс два раза в тригонометрические функции, сначала в синус , а потом в котангенс :

\(x → sin⁡x → ctg⁡ (sin⁡x )\)

Напиши теперь сам функции, где икс:
— сначала «упаковывается» в косинус, а потом в показательную функцию с основанием \(3\);
— сначала в пятую степень, а затем в тангенс;
— сначала в логарифм по основанию \(4\) , затем в степень \(-2\).

Ответы на это задание посмотри в конце статьи.

А можем ли мы «упаковать» икс не два, а три раза? Да, без проблем! И четыре, и пять, и двадцать пять раз. Вот, например, функция, в которой икс «упакован» \(4\) раза:

Но такие формулы в школьной практике не встретятся (студентам повезло больше — у них может быть и посложнее☺).

«Распаковка» сложной функции

Посмотри на предыдущую функцию еще раз. Сможешь ли ты разобраться в последовательности «упаковки»? Во что икс запихнули сначала, во что потом и так далее до самого конца. То есть — какая функция вложена в какую? Возьми листок и запиши, как ты считаешь. Можно сделать это цепочкой со стрелками как мы писали выше или любым другим способом.

Теперь правильный ответ: сначала икс «упаковали» в \(4\)-ую степень, потом результат упаковали в синус, его в свою очередь поместили в логарифм по основанию \(2\), и в конце концов всю эту конструкцию засунули в степень пятерки.

То есть разматывать последовательность надо В ОБРАТНОМ ПОРЯДКЕ. И тут подсказка как это делать проще: сразу смотри на икс – от него и надо плясать. Давай разберем несколько примеров.

Например, вот такая функция: \(y=tg⁡(\log_2⁡x )\). Смотрим на икс – что с ним происходит сначала? Берется логарифм от него. А потом? Берется тангенс от результата. Вот и последовательность будет такая же:

\(x → \log_2⁡x → tg⁡(\log_2⁡x )\)

Еще пример: \(y=\cos⁡<(x^3 )>\). Анализируем – сначала икс возвели в куб, а потом от результата взяли косинус. Значит, последовательность будет: \(x → x^3 → \cos⁡<(x^3 )>\). Обрати внимание, функция вроде бы похожа на самую первую (там, где с картинками). Но это совсем другая функция: здесь в кубе икс (то есть \(\cos⁡<(x·x·x)>)\), а там в кубе косинус \(x\) (то есть, \(\cos⁡x·\cos⁡x·\cos⁡x\)). Эта разница возникает из-за разных последовательностей «упаковки».

Последний пример (с важной информацией в нем): \(y=\sin⁡<(2x+5)>\). Понятно, что здесь сначала сделали арифметические действия с иксом, потом от результата взяли синус: \(x → 2x+5 → \sin⁡<(2x+5)>\). И это важный момент: несмотря на то, что арифметические действия функциями сами по себе не являются, здесь они тоже выступают как способ «упаковки». Давай немного углубимся в эту тонкость.

Как я уже говорил выше, в простых функциях икс «упаковывается» один раз, а в сложных — два и более. При этом любая комбинация простых функций (то есть их сумма, разность, умножение или деление) — тоже простая функция. Например, \(x^7\) – простая функция и \(ctg x\) — тоже. Значит и все их комбинации являются простыми функциями:

\(x^7+ ctg x\) — простая,
\(x^7· ctg x\) – простая,
\(\frac\) – простая и т.д.

Однако если к такой комбинации применить еще одну функцию – будет уже сложная функция, так как «упаковок» станет две. Смотри схему:

Хорошо, давай теперь сам. Напиши последовательность «заворачивания» функций:
\(y=cos<⁡(sin⁡x)>\)
\(y=5^\)
\(y=arctg⁡<11^x>\)
\(y=log_2⁡(1+x)\)
Ответы опять в конце статьи.

Внутренняя и внешняя функции

Зачем же нам нужно разбираться во вложенности функций? Что нам это дает? Дело в том, что без такого анализа мы не сможем надежно находить производные разобранных выше функций.

И для того, чтобы двигаться дальше, нам будут нужны еще два понятия: внутренняя и внешняя функции. Это очень простая вещь, более того, на самом деле мы их уже разобрали выше: если вспомнить нашу аналогию в самом начале, то внутренняя функция — это «пакет», а внешняя – это «коробка». Т.е. то, во что икс «заворачивают» сначала – это внутренняя функция, а то, во что «заворачивают» внутреннюю – уже внешняя. Ну, понятно почему – она ж снаружи, значит внешняя.

Вот в этом примере: \(y=tg⁡(log_2⁡x )\), функция \(\log_2⁡x\) – внутренняя, а — внешняя.

А в этом: \(y=\cos⁡<(x^3+2x+1)>\), \(x^3+2x+1\) — внутренняя, а — внешняя.

Выполни последнюю практику анализа сложных функций, и перейдем, наконец, к тому, ради чего всё затевалось — будем находить производные сложных функций:

Заполни пропуски в таблице:

Производная сложной функции

Браво нам, мы всё ж таки добрались до «босса» этой темы – собственно, производной сложной функции, а конкретно, до той самой ужасной формулы из начала статьи.☺

Формула эта читается так:

Производная сложной функции равна произведению производной внешней функции по неизменной внутренней на производную внутренней функции.

И сразу смотри схему разбора «по словам» чтобы понимать, что к чему относится:

Надеюсь, термины «производная» и «произведение» затруднений не вызывают. «Сложную функцию» — мы уже разобрали. Загвоздка в «производной внешней функции по неизменной внутренней». Что это такое?

Ответ: это обычная производная внешней функции, при которой изменяется только внешняя функция, а внутренняя остается такой же. Все равно непонятно? Хорошо, давай на примере.

Пусть у нас есть функция \(y=\sin⁡(x^3 )\). Понятно, что внутренняя функция здесь \(x^3\), а внешняя . Найдем теперь производную внешней по неизменной внутренней.

Из таблицы производных мы знаем, что производная синуса икс есть косинус икс (табличные значения надо знать наизусть!): \((<\sin⁡>)’=\cos⁡\).

Тогда производная внешней функции по неизменной внутренней для нашего случая будет \(\cos⁡(x^3)\). То есть, мы взяли ее как обычную производную синуса, а содержимое синуса (внутреннюю функцию) просто скопировали в полученную производную (косинус), ничего в ней не меняя.

Таким образом, на данный момент имеем:

Осталась «производная внутренней функции». Ну, это совсем легко – обычная производная от внутренней функции, при этом внешняя не влияет вообще никак. В нашем примере, производная от \(x^3\).

Все, теперь можем писать ответ:

Вот так. Давай еще один пример разберем.

Пусть надо найти производную функции \(y=(\sin⁡x )^3\).

Анализируем. Последовательность «заворачивания» у нас такая: \(x → \sin⁡x → (\sin⁡x )^3\). Значит, в данном примере внутренняя функция это \(\sin⁡x\), а внешняя .

Производная внешней по внутренней – это производная куба (содержимое куба при этом не меняется). Так как , а в нашем случае в куб «завернут» \(\sin⁡x\), то производная внешней будет \(3(\sin⁡x)^2\). То есть, имеем:

Ну, а производная внутренней – это просто производная синуса икс, то есть косинус икс.

Понятно?
Ладно, ладно, вот еще один пример с разбором. ☺

Пример. Найти производную сложной функции \(y=\ln(x^2-x)\).

Разбираем вложенность функций: \(x → x^2-x → \ln⁡(x^2-x)\).
Внутренняя: \(x^2-x\). Внешняя: .
Из таблицы производных знаем:.
То есть производная внешней по внутренней будет: \(\ln⁡(x^2-x)’=\) \(\frac<1>\) .
Производная внутренней: \((x^2-x)’= (x^2)’-(x)’=2x-1\).
В итоге, согласно большой и страшной формуле имеем:

Ну и напоследок можно немного «причесать» ответ, чтоб никто не докопался:

Что, еще примеров желаешь? Легко.

Пример. Найти производную сложной функции \(y=\sin⁡<(\cos⁡x)>\).
Вложенность функций: \(x → \cos⁡x → \sin⁡<(\cos⁡x)>\)
Внутренняя: \(\cos⁡x\) Внешняя:
Производная внешней по внутренней: \(\sin<⁡(\cos⁡x )>‘=\cos⁡<\cos⁡x>\)
Производная внутренней: \((\cos⁡x )’= -\sin⁡x\)
Имеем: \(y’=(\sin⁡<(\cos⁡x)>)’=\cos⁡<\cos⁡x>·(-\sin⁡x )=-\cos⁡ <\cos⁡x>·\sin⁡x\)

Замечание: Обрати внимание, что заменить запись \(\cos⁡<\cos⁡x>\) на \(\cos^2⁡x\) НЕЛЬЗЯ, так как \(\cos^2⁡x\) — это комбинация простых функций \(\cos^ 2⁡x=\cos⁡x·\cos⁡x\), а \(\cos⁡<\cos⁡x>\) – сложная функция: косинус от косинуса икс. Это абсолютно разные функции.

Еще пример с важным замечанием в нем.

Пример. Найти производную сложной функции \(y=\sqrt \)
Вложенность функций: \(x → x^6 → \sqrt\)
Внутренняя: \(x^6\) Внешняя:
Производная внешней по внутренней: \(\sqrt‘=\) \(\frac<1><2\sqrt>\)
Производная внутренней: \((x^6)’= 6x^5\)
Имеем: \((\sqrt)’=\) \(\frac<1><2\sqrt>\) \(·6x^5\)
И теперь упростим ответ. Вспомним свойство корня: \(\sqrt[b] =x^<\frac>\). Тогда \(\sqrt=x^<\frac<6><2>>=x^3\). С учетом этого получаем:

Всё. А теперь, собственно, важное замечание:

Давай рассмотрим пример, где эта идея нам сильно поможет.

Пример. Найти производную сложной функции \(y=\ln⁡(x^3)\).
Можно, конечно, рассмотреть вложенность функций: \(x → x^3 → \ln⁡(x^3 )\), разобрать на внутреннюю и внешнюю и так далее. Но можно вспомнить свойство логарифма: \(\log_a⁡=c·\log_a<⁡b>\). И тогда функция получается \(y=\ln⁡(x^3 )=3\ln⁡x\). Отлично! Берем производную:

Теперь задачка посложнее, для продвинутых. Решим пример с тройной вложенностью!

Пример. Найти производную сложной функции \(y=3^<\sin⁡(x^4+1)>\).
Вложенность функций: \(x → x^4+1 → \sin⁡(x^4+1) → 3^<\sin⁡(x^4+1)>\)
Внутренняя: \(x^4+1\) Средняя: Внешняя:
Сначала производная внешней по средней. Вспоминаем таблицу производных: . Значит, в нашем случае будет \(3^<\sin⁡(x^4+1)>·\ln⁡3\).
Хорошо, теперь производная средней по внутренней. По таблице: . Значит, мы получим, \(\sin⁡(x^4+1)’=\cos⁡(x^4+1)\).
И наконец, производная внутренней: \((x^4+1)’=(x^4 )’+(1)’=4x^3\).
Отлично. Теперь собираем все вместе, перемножая отдельные производные:

Готово. Да, это ответ. ☺

Ну, а что ты хотел, я сразу сказал – пример для продвинутых! А представь, что будет с четырехкратной или пятикратной вложенностью? ☺

Пример: Найти производную сложной функции \(y=tg⁡(7^x)\).

Разбираем вложенность функций: \(x \: → \:7^x \: → \:tg⁡(7^x)\).
Внутренняя: \(7^x\) Внешняя: \(tg⁡(7^x)\).
Ищем производную самой внешней функции, внутреннюю при этом не трогаем.
Из таблицы производных знаем: .
То есть, в нашем случае производная внешней по внутренней будет: \(\frac<1><\cos^2⁡(7^x)>\) .
Теперь ищем производную внутренней. Этой формулой мы уже пользовались, так что сразу пишем ответ: \((7^x)’=7^x·\ln⁡7\).
И перемножаем результаты:

Ну, теперь думаю всё понятно? И снова повторю – не пугайся сложных конструкций в ответах и промежуточных вычислениях. Они «на лицо ужасные», но зато добрые (в смысле простые) внутри. ☺ Пойми принцип и делай все последовательно.

Последний пример. Такие задания в разных вариациях весьма часто дают на контрольных и тестах. Он вроде как считается сложным. ☺ Хех, наивные учителя. ☺

Пример: Найти производную сложной функции \(y=\sqrt[3]<(x^5+2x-5)^2>\).

Казалось бы, опять у нас тройная вложенность функций:

Но давай снова воспользуемся свойством корня \(\sqrt[b] =x^<\frac>\) и преобразуем нашу функцию к виду:

Вот так. И теперь у нас вложенность двойная: \(x → x^5+2x-5 → (x^5+2x-5)^<\frac<2><3>>\)
При этом функция осталась той же! Удобное свойство, однако. Стоит его запомнить, да? ☺ Ладно, поехали дальше.
Внутренняя функция: \(x^5+2x-5\). Внешняя: .
Производная внешней по внутренней. По таблице производных общая формула производной степенной функции: . Получаем: . Тогда в нашем случае будет: \(\frac<2><3>(x^5+2x-5)^<-\frac<1><3>>\).
Производная внутренней: \((x^5+2x-5)’=5x^4+2\).
Общий результат: \(y ‘=(\sqrt[3]<(x^5+2x-5)^2>)’=((x^5+2x-5)^<\frac<2><3>> )’=\frac<2><3>(x^5+2x-5)^<-\frac<1><3>>·(5x^4+2)\).

В принципе, ответ найден. Но здесь можно сильно «причесать» результаты. Это может показаться сложным, но это не так, просто опять нагромождения символов большое и возникает такое ложное ощущение. На всякий случай помни: «не причесанный» ответ – тоже ответ. Поэтому если не поймешь дальнейших преобразований – не критично. Ладно, расческу в руки и вперед.
Вспоминаем свойство отрицательной степени \(a^<-n>=\) \(\frac<1>\) . Получаем:

Ну, и перемножаем дроби.

ВСЁ. А теперь сам.

Найти производные функций:

Ответы ко всем заданиям (вперемежку).

\(x → 1+x → \log_2⁡ <(1+x)>\)
\(x → 11^x → arctg⁡(11^x) \)
\(x → x^7 → 5^\)
\(x → \sin⁡x → \cos⁡(\sin⁡x)\)

Производная сложной функции

Функции сложного вида не всегда подходят под определение сложной функции. Если имеется функция вида y = sin x — ( 2 — 3 ) · a r c t g x x 5 7 x 10 — 17 x 3 + x — 11 , то ее нельзя считать сложной в отличие от y = sin 2 x .

Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.

Основные определения

Сложной функцией считается такая функция, у которой аргумент также является функцией.

Обозначается это таким образом: f ( g ( x ) ) . Имеем, что функция g ( x ) считается аргументом f ( g ( x ) ) .

Если есть функция f и является функцией котангенса, тогда g ( x ) = ln x – это функция натурального логарифма. Получаем, что сложная функция f ( g ( x ) ) запишется как arctg(lnx). Или функция f , являющаяся функцией возведенной в 4 степень, где g ( x ) = x 2 + 2 x — 3 считается целой рациональной функцией, получаем, что f ( g ( x ) ) = ( x 2 + 2 x — 3 ) 4 .

Очевидно, что g ( x ) может быть сложной. Из примера y = sin 2 x + 1 x 3 — 5 видно, что значение g имеет кубический корень с дробью. Данное выражение разрешено обозначать как y = f ( f 1 ( f 2 ( x ) ) ) . Откуда имеем, что f – это функция синуса, а f 1 — функция, располагаемая под квадратным корнем, f 2 ( x ) = 2 x + 1 x 3 — 5 — дробная рациональная функция.

Степень вложенности определено любым натуральным числом и записывается как y = f ( f 1 ( f 2 ( f 3 ( . . . ( f n ( x ) ) ) ) ) ) .

Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида

( f ( g ( x ) ) ) ‘ = f ‘ ( g ( x ) ) · g ‘ ( x )

Примеры

Найти производную сложной функции вида y = ( 2 x + 1 ) 2 .

По условию видно, что f является функцией возведения в квадрат, а g ( x ) = 2 x + 1 считается линейной функцией.

Применим формулу производной для сложной функции и запишем:

f ‘ ( g ( x ) ) = ( ( g ( x ) ) 2 ) ‘ = 2 · ( g ( x ) ) 2 — 1 = 2 · g ( x ) = 2 · ( 2 x + 1 ) ; g ‘ ( x ) = ( 2 x + 1 ) ‘ = ( 2 x ) ‘ + 1 ‘ = 2 · x ‘ + 0 = 2 · 1 · x 1 — 1 = 2 ⇒ ( f ( g ( x ) ) ) ‘ = f ‘ ( g ( x ) ) · g ‘ ( x ) = 2 · ( 2 x + 1 ) · 2 = 8 x + 4

Необходимо найти производную с упрощенным исходным видом функции. Получаем:

y = ( 2 x + 1 ) 2 = 4 x 2 + 4 x + 1

Отсюда имеем, что

y ‘ = ( 4 x 2 + 4 x + 1 ) ‘ = ( 4 x 2 ) ‘ + ( 4 x ) ‘ + 1 ‘ = 4 · ( x 2 ) ‘ + 4 · ( x ) ‘ + 0 = = 4 · 2 · x 2 — 1 + 4 · 1 · x 1 — 1 = 8 x + 4

При решении задач такого вида важно понимать, где будет располагаться функция вида f и g ( x ) .

Следует найти производные сложных функций вида y = sin 2 x и y = sin x 2 .

Первая запись функции говорит о том, что f является функцией возведения в квадрат, а g ( x ) – функцией синуса. Тогда получим, что

y ‘ = ( sin 2 x ) ‘ = 2 · sin 2 — 1 x · ( sin x ) ‘ = 2 · sin x · cos x

Вторая запись показывает, что f является функцией синуса, а g ( x ) = x 2 обозначаем степенную функцию. Отсюда следует, что произведение сложной функции запишем как

y ‘ = ( sin x 2 ) ‘ = cos ( x 2 ) · ( x 2 ) ‘ = cos ( x 2 ) · 2 · x 2 — 1 = 2 · x · cos ( x 2 )

Формула для производной y = f ( f 1 ( f 2 ( f 3 ( . . . ( f n ( x ) ) ) ) ) ) запишется как y ‘ = f ‘ ( f 1 ( f 2 ( f 3 ( . . . ( f n ( x ) ) ) ) ) ) · f 1 ‘ ( f 2 ( f 3 ( . . . ( f n ( x ) ) ) ) ) · · f 2 ‘ ( f 3 ( . . . ( f n ( x ) ) ) ) · . . . · f n ‘ ( x )

Найти производную функции y = sin ( ln 3 a r c t g ( 2 x ) ) .

Данный пример показывает сложность записи и определения расположения функций. Тогда y = f ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) обозначим, где f , f 1 , f 2 , f 3 , f 4 ( x ) является функцией синуса, функцией возведения в 3 степень, функцией с логарифмом и основанием е , функцией арктангенса и линейной.

Из формулы определения сложной функции имеем, что

y ‘ = f ‘ ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) · f 1 ‘ ( f 2 ( f 3 ( f 4 ( x ) ) ) ) · · f 2 ‘ ( f 3 ( f 4 ( x ) ) ) · f 3 ‘ ( f 4 ( x ) ) · f 4 ‘ ( x )

Получаем, что следует найти

1. f ‘ ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) в качестве производной синуса по таблице производных, тогда f ‘ ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) = cos ( ln 3 a r c t g ( 2 x ) ) .
2. f 1 ‘ ( f 2 ( f 3 ( f 4 ( x ) ) ) ) в качестве производной степенной функции, тогда f 1 ‘ ( f 2 ( f 3 ( f 4 ( x ) ) ) ) = 3 · ln 3 — 1 a r c t g ( 2 x ) = 3 · ln 2 a r c t g ( 2 x ) .
3. f 2 ‘ ( f 3 ( f 4 ( x ) ) ) в качестве производной логарифмической, тогда f 2 ‘ ( f 3 ( f 4 ( x ) ) ) = 1 a r c t g ( 2 x ) .
4. f 3 ‘ ( f 4 ( x ) ) в качестве производной арктангенса, тогда f 3 ‘ ( f 4 ( x ) ) = 1 1 + ( 2 x ) 2 = 1 1 + 4 x 2 .
5. При нахождении производной f 4 ( x ) = 2 x произвести вынесение 2 за знак производной с применением формулы производной степенной функции с показателем, который равняется 1 , тогда f 4 ‘ ( x ) = ( 2 x ) ‘ = 2 · x ‘ = 2 · 1 · x 1 — 1 = 2 .

Производим объединение промежуточных результатов и получаем, что

y ‘ = f ‘ ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) · f 1 ‘ ( f 2 ( f 3 ( f 4 ( x ) ) ) ) · · f 2 ‘ ( f 3 ( f 4 ( x ) ) ) · f 3 ‘ ( f 4 ( x ) ) · f 4 ‘ ( x ) = = cos ( ln 3 a r c t g ( 2 x ) ) · 3 · ln 2 a r c t g ( 2 x ) · 1 a r c t g ( 2 x ) · 1 1 + 4 x 2 · 2 = = 6 · cos ( ln 3 a r c t g ( 2 x ) ) · ln 2 a r c t g ( 2 x ) a r c t g ( 2 x ) · ( 1 + 4 x 2 )

Разбор таких функций напоминает матрешки. Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.

Существуют некоторые различия сложного вида от сложных функций. При явном умении это различать, нахождение производных будет давать особенно легко.

Необходимо рассмотреть на приведении подобного примера. Если имеется функция вида y = t g 2 x + 3 t g x + 1 , тогда ее можно рассмотреть в качестве сложной вида g ( x ) = t g x , f ( g ) = g 2 + 3 g + 1 . Очевидно, что необходимо применение формулы для сложной производной:

f ‘ ( g ( x ) ) = ( g 2 ( x ) + 3 g ( x ) + 1 ) ‘ = ( g 2 ( x ) ) ‘ + ( 3 g ( x ) ) ‘ + 1 ‘ = = 2 · g 2 — 1 ( x ) + 3 · g ‘ ( x ) + 0 = 2 g ( x ) + 3 · 1 · g 1 — 1 ( x ) = = 2 g ( x ) + 3 = 2 t g x + 3 ; g ‘ ( x ) = ( t g x ) ‘ = 1 cos 2 x ⇒ y ‘ = ( f ( g ( x ) ) ) ‘ = f ‘ ( g ( x ) ) · g ‘ ( x ) = ( 2 t g x + 3 ) · 1 cos 2 x = 2 t g x + 3 cos 2 x

Функция вида y = t g x 2 + 3 t g x + 1 не считается сложной, так как имеет сумму t g x 2 , 3 t g x и 1 . Однако, t g x 2 считается сложной функцией, то получаем степенную функцию вида g ( x ) = x 2 и f , являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что

y ‘ = ( t g x 2 + 3 t g x + 1 ) ‘ = ( t g x 2 ) ‘ + ( 3 t g x ) ‘ + 1 ‘ = = ( t g x 2 ) ‘ + 3 · ( t g x ) ‘ + 0 = ( t g x 2 ) ‘ + 3 cos 2 x

Переходим к нахождению производной сложной функции ( t g x 2 ) ‘ :

f ‘ ( g ( x ) ) = ( t g ( g ( x ) ) ) ‘ = 1 cos 2 g ( x ) = 1 cos 2 ( x 2 ) g ‘ ( x ) = ( x 2 ) ‘ = 2 · x 2 — 1 = 2 x ⇒ ( t g x 2 ) ‘ = f ‘ ( g ( x ) ) · g ‘ ( x ) = 2 x cos 2 ( x 2 )

Получаем, что y ‘ = ( t g x 2 + 3 t g x + 1 ) ‘ = ( t g x 2 ) ‘ + 3 cos 2 x = 2 x cos 2 ( x 2 ) + 3 cos 2 x

Функции сложного вида могут быть включены в состав сложных функций, причем сами сложные функции могут являться составными функции сложного вида.

Для примера рассмотрим сложную функцию вида y = log 3 x 2 + 3 cos 3 ( 2 x + 1 ) + 7 e x 2 + 3 3 + ln 2 x · ( x 2 + 1 )

Данная функция может быть представлена в виде y = f ( g ( x ) ) , где значение f является функцией логарифма по основанию 3 , а g ( x ) считается суммой двух функций вида h ( x ) = x 2 + 3 cos 3 ( 2 x + 1 ) + 7 e x 2 + 3 3 и k ( x ) = ln 2 x · ( x 2 + 1 ) . Очевидно, что y = f ( h ( x ) + k ( x ) ) .

Рассмотрим функцию h ( x ) . Это отношение l ( x ) = x 2 + 3 cos 3 ( 2 x + 1 ) + 7 к m ( x ) = e x 2 + 3 3

Имеем, что l ( x ) = x 2 + 3 cos 2 ( 2 x + 1 ) + 7 = n ( x ) + p ( x ) является суммой двух функций n ( x ) = x 2 + 7 и p ( x ) = 3 cos 3 ( 2 x + 1 ) , где p ( x ) = 3 · p 1 ( p 2 ( p 3 ( x ) ) ) является сложной функцией с числовым коэффициентом 3 , а p 1 — функцией возведения в куб, p 2 функцией косинуса, p 3 ( x ) = 2 x + 1 — линейной функцией.

Получили, что m ( x ) = e x 2 + 3 3 = q ( x ) + r ( x ) является суммой двух функций q ( x ) = e x 2 и r ( x ) = 3 3 , где q ( x ) = q 1 ( q 2 ( x ) ) — сложная функция, q 1 — функция с экспонентой, q 2 ( x ) = x 2 — степенная функция.

Отсюда видно, что h ( x ) = l ( x ) m ( x ) = n ( x ) + p ( x ) q ( x ) + r ( x ) = n ( x ) + 3 · p 1 ( p 2 ( p 3 ( x ) ) ) q 1 ( q 2 ( x ) ) + r ( x )

При переходе к выражению вида k ( x ) = ln 2 x · ( x 2 + 1 ) = s ( x ) · t ( x ) видно, что функция представлена в виде сложной s ( x ) = ln 2 x = s 1 ( s 2 ( x ) ) с целой рациональной t ( x ) = x 2 + 1 , где s 1 является функцией возведения в квадрат, а s 2 ( x ) = ln x — логарифмической с основанием е .

Отсюда следует, что выражение примет вид k ( x ) = s ( x ) · t ( x ) = s 1 ( s 2 ( x ) ) · t ( x ) .

Тогда получим, что

y = log 3 x 2 + 3 cos 3 ( 2 x + 1 ) + 7 e x 2 + 3 3 + ln 2 x · ( x 2 + 1 ) = = f n ( x ) + 3 · p 1 ( p 2 ( p 3 ( x ) ) ) q 1 ( q 2 ( x ) ) = r ( x ) + s 1 ( s 2 ( x ) ) · t ( x )

По структурам функции стало явно, как и какие формулы необходимо применять для упрощения выражения при его дифференцировании. Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной.

Примеры применения формулы производной сложной функции

Основные формулы

Здесь мы приводим примеры вычисления производных от следующих функций:
; ; ; ; .

Если функцию можно представить как сложную функцию в следующем виде:
,
то ее производная определяется по формуле:
.
В приводимых ниже примерах, мы будем записывать эту формулу в следующем виде:
.
где .
Здесь нижние индексы или , расположенные под знаком производной, обозначают переменные, по которой выполняется дифференцирование.

Обычно, в таблицах производных, приводятся производные функций от переменной x . Однако x – это формальный параметр. Переменную x можно заменить любой другой переменной. Поэтому, при дифференцировании функции от переменной , мы просто меняем, в таблице производных, переменную x на переменную u .

Простые примеры

Пример 1

Найти производную сложной функции
.

Запишем заданную функцию в эквивалентном виде:
.
В таблице производных находим:
;
.

По формуле производной сложной функции имеем:
.
Здесь .

Пример 2

Выносим постоянную 5 за знак производной и из таблицы производных находим:
.

Применяем формулу производной сложной функции:
.
Здесь .

Пример 3

Выносим постоянную –1 за знак производной и из таблицы производных находим:
;
Из таблицы производных находим:
.

Применяем формулу производной сложной функции:
.
Здесь .

Более сложные примеры

В более сложных примерах мы применяем правило дифференцирования сложной функции несколько раз. При этом мы вычисляем производную с конца. То есть разбиваем функцию на составные части и находим производные самых простых частей, используя таблицу производных. Также мы применяем правила дифференцирования суммы, произведения и дроби. Затем делаем подстановки и применяем формулу производной сложной функции.

Пример 4

Выделим самую простую часть формулы и найдем ее производную. .

Применяем правило дифференцирования сложной функции.

.
Здесь мы использовали обозначение
.

Находим производную следующей части исходной функции, применяя полученные результаты. Применяем правило дифференцирования суммы:
.

Еще раз применяем правило дифференцирования сложной функции.

.
Здесь .

Пример 5

Найдите производную функции
.

Выделим самую простую часть формулы и из таблицы производных найдем ее производную. .

Применяем правило дифференцирования сложной функции.
.
Здесь
.

Дифференцируем следующую часть, применяя полученные результаты.
.
Здесь
.

Дифференцируем следующую часть.

.
Здесь
.

Теперь находим производную искомой функции.

.
Здесь
.

Автор: Олег Одинцов . Опубликовано: 19-11-2016