Как решать
показательные уравнения?
Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.
Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной \(х\) не в основании степени, а в самом показателе. Как это выглядит:
Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение \(х\). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо \(х\) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
Значит, если \(х=3\), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь посложнее.
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
Мы применили свойство отрицательной степени по формуле:
Теперь наше уравнение будет выглядеть так:
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны \(3\), только вот степени разные – слева степень \((4х-1)\), а справа \((-2)\). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
Поздравляю, мы нашли корень нашего показательного уравнения.
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что \(125=5*5*5=5^3\), а \(25=5*5=5^2\), подставим:
Воспользуемся одним из свойств степеней \((a^n)^m=a^
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
И еще один пример:
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить \(2\) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
Где \(a,b\) какие-то положительные числа. (\(a>0, \; b>0\).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит \(a^x\), с этим ничего делать не будем, а вот справа у нас стоит загадочное число \(b\), которое нужно попытаться представить в виде \(b=a^m\). Тогда уравнение принимает вид:
Раз основания одинаковые, то мы можем просто приравнять степени:
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Замечаем, что \(16=2*2*2*2=2^4\) это степень двойки:
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6 $$5^<-x>=125 \Rightarrow 5^<-x>=5*5*5 \Rightarrow 5^<-x>=5^3 \Rightarrow –x=3 \Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 \Rightarrow (3*3)^<4x>=3*3*3*3 \Rightarrow(3^2)^<4x>=3^4 \Rightarrow 3^<8x>=3^4 \Rightarrow 8x=4 \Rightarrow x=\frac<1><2>.$$
Здесь мы заметили, что \(9=3^2\) и \(81=3^4\) являются степенями \(3\).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
\(3\) и \(2\) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число \(b>0\), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице \(a>0, \; a \neq 1\):
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим \(2\) в виде \(3\) в какой-то степени, где \(a=3\), а \(b=2\):
Подставим данное преобразование в наш пример:
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: \(a^x=b\), где \(a>0; \; b>0\).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа \(a^x=b\), где \(a>0; \; b>0\). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что \(9=3^2\), тогда \(9^x=(3^2)^x=3^<2x>=(3^x)^2\). Здесь мы воспользовались свойством степеней: \((a^n)^m=a^
Обратим внимание, что во всем уравнении все \(х\) «входят» в одинаковую функцию — \(3^x\). Сделаем замену \(t=3^x, \; t>0\), так как показательная функция всегда положительна.
Квадратное уравнение, которое решается через дискриминант:
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
И второй корень:
И еще один пример на замену:
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание \(3\). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член \(3=2+1\) и вынести общий множитель \(2\):
Подставим в исходное уравнение:
Теперь показательные функции одинаковы и можно сделать замену:
Обратная замена, и наше уравнение сводится к простейшему:
И второе значение \(t\):
Тут у нас две показательные функции с основаниями \(7\) и \(3\), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на \(3^x\):
Здесь нам придется воспользоваться свойствами степеней:
Разберем каждое слагаемое:
Теперь подставим получившееся преобразования в исходное уравнение:
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену \(t=(\frac<7><3>)^x\):
Сделаем обратную замену:
И последний пример на замену:
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
Разберем каждое слагаемое нашего уравнения:
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!
И последнее слагаемое со степенью:
Подставим все наши преобразования в исходное уравнение:
Теперь можно сделать замену \(t=2^x\) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель \(2^x\)):
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании \(2\), \(5\) и \(10\). Очевидно, что \(10=2*5\). Воспользуемся этим и подставим в наше уравнение:
Воспользуемся формулой \((a*b)^n=a^n*b^n\):
И перекинем все показательные функции с основанием \(2\) влево, а с основанием \(5\) вправо:
Сокращаем и воспользуемся формулами \(a^n*a^m=a^
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Показательные уравнения в математике с примерами решения и образцами выполнения
Простейшее показательное уравнение — это уравнение вида 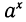
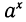
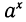
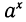
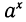
Сформулируем общий результат о решении простейшего показательного уравнения (схема XI).
Теорема:
Пусть а > 0 и а ≠ 1. Уравнение 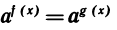
Доказательство:
Докажем, что если 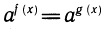
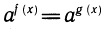
Примеры:
Простейшее логарифмическое уравнение — это уравнение вида logax=b. Оно имеет единственное решение х — а при любом b.
Сформулируем общий результат о решении простейшего логарифмического уравнения (схема XI).
Теорема:
Уравнение ioga f (х) = loga g (х) равносильно уравнению f(x)=g(x) при ограничениях f (х)> 0, g(x)>0.
Доказательство:
Пусть х — решение уравнения
Тогда определены логарифмы чисел f (х) и g (х), т. е. эти числа должны быть больше нуля. Потенцируя равенство 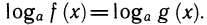
Примеры:
Мы решили уравнение х— 1 = 5 — х, а затем проверили, удовлетворяет ли решение условиям х— 1 >0 и 5 — х>0. Заметим, что если f (x) = g (х) и f (х)>0, то тогда и g (x)>0, т. е. из двух неравенств достаточно проверить только одно.
Показательные уравнения справочные сведения
Показательная функция 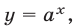
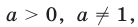
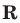
2.Для любых 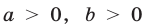
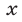
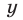
3. Простейшее показательное уравнение
не имеет корней при 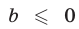
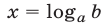
В частности, уравнение 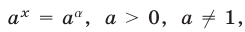
4.Уравнение
5.Уравнение
равносильно каждому из уравнений
Примеры с решениями
Пример:
Решить уравнение
Решение:
Данное уравнение равносильно каждому из уравнений 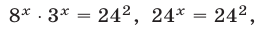
Ответ.
Пример:
Решить уравнение
Решение:
Это уравнение равносильно каждому из уравнений:
откуда находим
Ответ.
Пример:
Решение:
Пусть 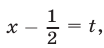
Это уравнение равносильно каждому из уравнений: 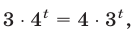
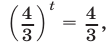
Ответ.
Пример:
Решение:
Полагая 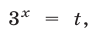
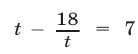
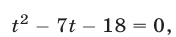
Следовательно, исходное уравнение равносильно совокупности уравнений 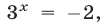
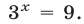
Ответ.
Пример:
Решение:
Запишем данное уравнение в виде
и заметим, что левая часть уравнения (2) — однородный многочлен степени 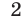
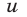
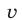
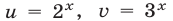
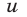
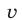
Разделив обе части уравнения (2) на 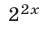
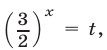
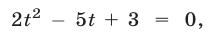
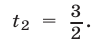
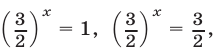
Ответ.
Пример:
Решение:
Воспользуемся равенством 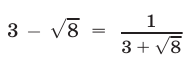
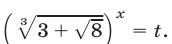
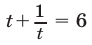
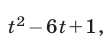
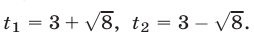
откуда
Ответ,
Пример:
Решение:
Число 2 является корнем этого уравнения. Докажем, что уравнение не имеет других корней. Так как каждая из функций 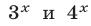
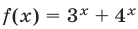
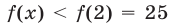
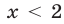
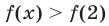
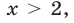
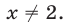
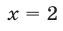
Показательные неравенства
Простейшее показательное неравенство — это неравенство вида 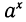
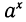
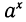
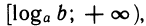
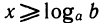
Пусть а>1 и b ≤ 0. Решением неравенства 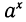
Можно сказать, что неравенство типа 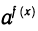
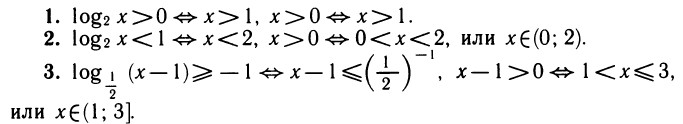
4. 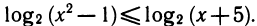
Основной прием, с помощью которого решают показательные и логарифмические уравнения и неравенства,— это введение новой неизвестной. Поясним этот прием на ряде примеров.
1) Выражение показательных функций друг через друга.
Рассмотрим выражения 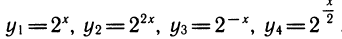
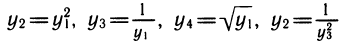
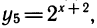
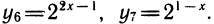
К этому полезно напомнить связь между различными основаниями. Например, 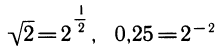
также нетрудно выразить через у1:
Если в уравнении или неравенстве встречается несколько показательных функций, то надо все их выразить через одну. Обычно после этого показательное уравнение или неравенство превращается в алгебраическое.
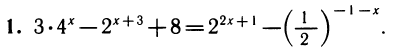
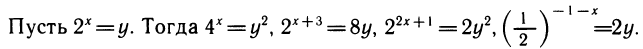
Делаем замену 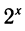
(мы умножили неравенство на у, что можно, так как
Так как 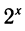
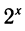
Используя модуль перехода, легко связать эти выражения между собой:
Свойства логарифмов позволяют по-разному записать связи между выражениями. Например,
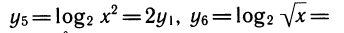
Если в уравнении или неравенстве встречается несколько логарифмических функций, то надо (если не удается избавиться от логарифмов потенцированием) выразить их через одну и свести логарифмическое уравнение или неравенство к алгебраическому.
Делаем замену lg х = у. Получаем уравнение относительно у:
Возвращаясь к неизвестной х, получим lg х = 2, х=100; lgx = 3, х= 1000.
Перейдем к основанию 3. Получим
заменив log3x на у, получим
Возвpащаясь к неизвестной х, получим log3x = 2, x = 9; log3x =—2,
Ответ:
Логарифмируя, получим равносильное данному неравенство (lg x —2) 1g x ≤ 3.
Положим lg х = у. Получим неравенство (у — 2)y ≤ З ⇔
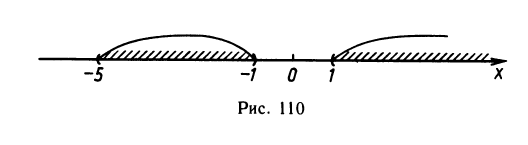
Возвращаясь к неизвестной х, получим — l ≤ lg x ≤ 3 ⇔ 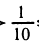
Ответ: 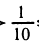
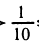
Использование свойства монотонности функций при решении показательных уравнений
Монотонность функций часто позволяет определить число корней уравнения, а иногда и найти их значения. Рассмотрим примеры решения уравнений.
В левой части уравнения имеем возрастающую функцию, а в правой — убывающую. Следовательно, уравнение не может иметь более одного корня (рис. 111). Один корень можно угадать: х=1. Это число и является окончательным ответом.
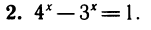
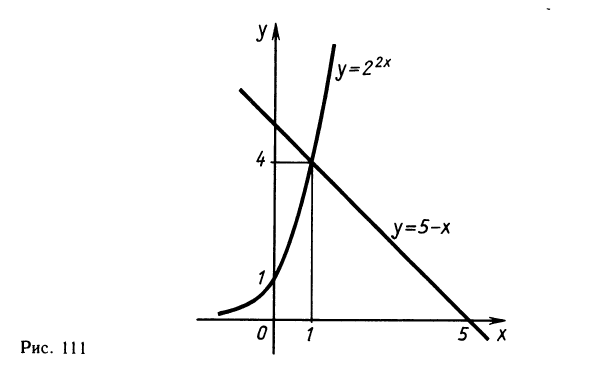
Одно решение х=1 легко найти подбором. Докажем, что других корней нет. Перепишем уравнение так:
В правой части последнего уравнения сумма убывающих функций т. е. значение у = 1 эта сумма может принять только один раз.
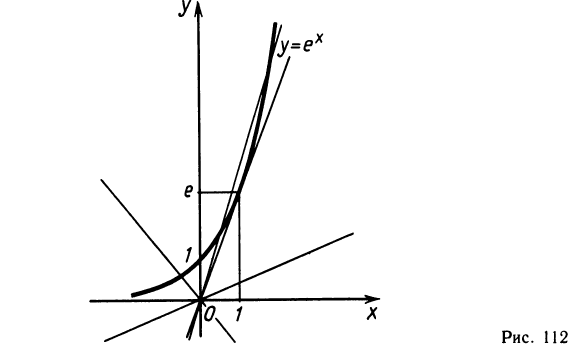
3. Сколько корней имеет уравнение 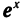
Изобразим схематически графики функций у = 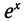
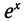
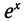
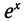
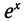
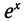
Ответ: при 0 ≤ а е два корня, при а = е один корень, при корней нет.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
Показательные уравнения и примеры решения
Определение. Уравнение называется показательным, если неизвестная входит в показатель степени.
Рассмотрим простейшие приемы решения показательных уравнений на отдельных примерах.
1. Решить уравнение
Представим левую и правую части уравнения в виде степеней, имеющих одинаковые основания:
Отсюда 3х = 2, или 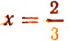
Мы здесь воспользовались следующей теоремой:
Если степени равны и основания равны, положительны и отличны от единицы, то равны и их показатели степеней.
Докажем эту теорему.
Пусть а > 1 и 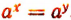
Допустим противное тому, что требуется доказать, т. е. допустим, что х > у или что х
3. Решить уравнение
Преобразуя левую часть уравнения, получим:
Значит, данное показательное уравнение имеет два корня:
4. Решить уравнение
Примем за новую неизвестную выражение 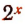
либо 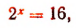
Из уравнения 
Из уравнения 
Итак, данное показательное уравнение имеет два корня: 4 и — 2.
5. Решить уравнение
Снова, обозначая 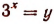
Таким образом, получим:
Как было указано при исследовании показательной функции, степень 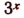
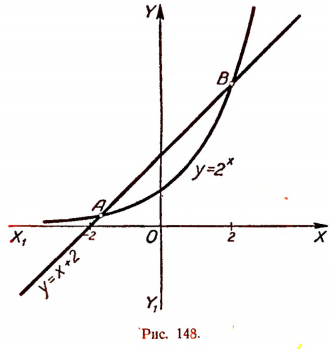
6. Решить уравнение
Для решения этого уравнения применим графический метод. Построим на одной координатной плоскости (рис. 148) графики функций:
Тогда абсциссы точек пересечения этих линий, т. е. абсциссы точек А и В, будут корнями данного уравнения. Абсцисса точки В, равная числу 2, будет точным корнем данного уравнения, а абсцисса точки А, равная приближенно —1,7, будет его приближенным корнем. Других корней данное уравнение не имеет.
Сведения, изложенные в этой главе, окажутся полезными при изучении логарифмов, которым посвящена следующая глава.
Примем к сведению без доказательства еще следующую теорему:
Если а есть положительной число, отличное от единицы, а N — любое положительное число, то уравнение 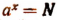
Примеры. Уравнение 
Уравнение 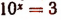
Итак, мы можем сделать следующие заключения:
- Выражение
, где а>0, имеет при каждом действительном значении х одно и только одно действительное значение.
- Действия над выражениями вида
, в которых х является любым действительным числом, можно выполнять по тем же правилам, по которым они выполняются над степенями с целым положительным показателем. Поэтому выражение
при всяком действительном значении х также называется степенью (обобщенной).
Примеры зависимостей, выражающихся с помощью показательных функций.
1. 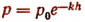
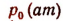
k —некоторая известная постоянная;
е —2,718;
h(м) —высота над уровнем моря;
р(ат) —давление на высоте А над уровнем моря.
Здесь h есть независимая переменная, или аргумент, а р есть зависимая переменная, или функция.
По этой формуле можно определять давление р по заданному значению h.
2. Если температура воздуха равна 20° С и тело в течение 20 минут охлаждается от 100 до 60°, то зависимость температуры Т охлаждающегося тела от времени t минут (в течение которого будет происходить охлаждение) выразится формулой
Здесь t есть аргумент, а Т—функция.
Пользуясь этой формулой, можно узнать, например, что через один час температура тела понизится до 30°.
Приведенные формулы выводятся в курсах высшей математики.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Показательные уравнения
О чем эта статья:
6 класс, 7 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
http://lfirmal.com/pokazatelnyie-uravneniya-primeryi-s-resheniem/
http://skysmart.ru/articles/mathematic/pokazatelnye-uravneniya
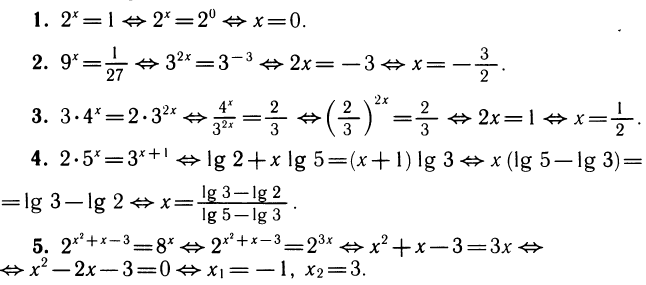
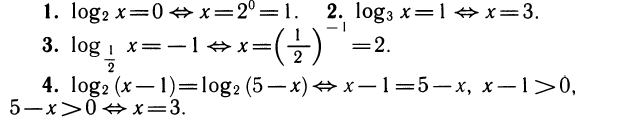
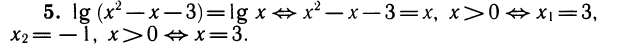

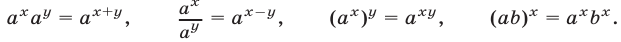
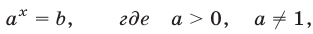
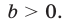
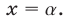
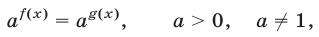
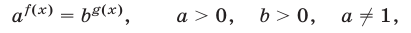
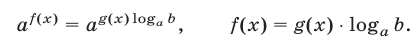
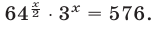
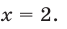
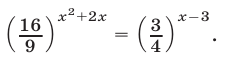
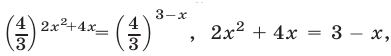
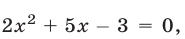
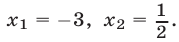
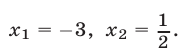
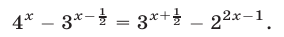
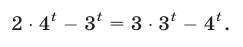
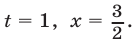
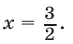
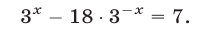
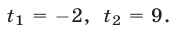
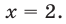
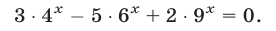
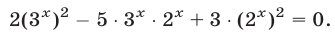
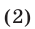
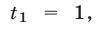
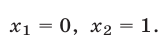
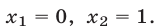
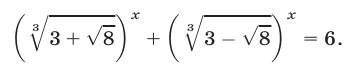
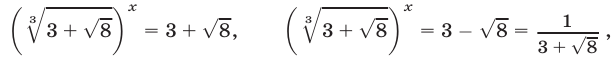
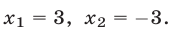
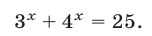
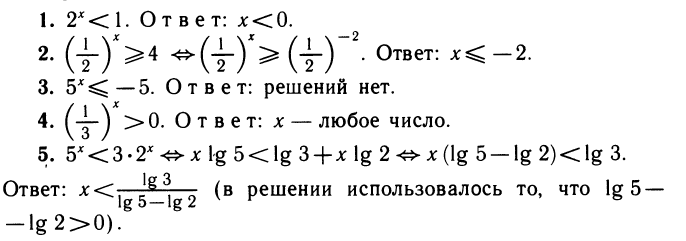
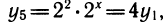
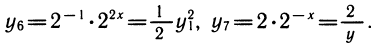
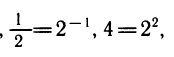
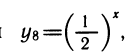
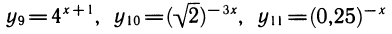
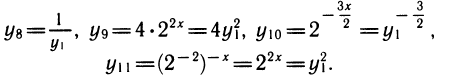
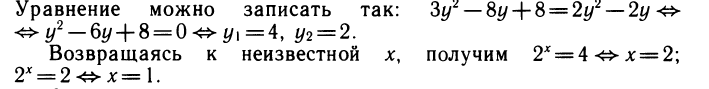
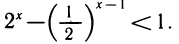
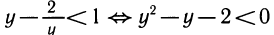

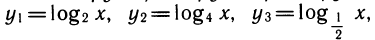
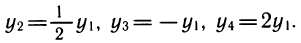
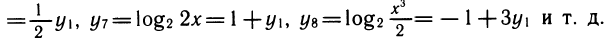
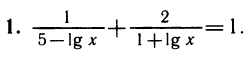
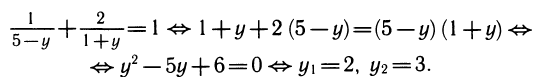
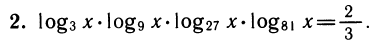
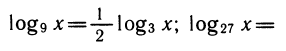
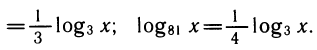
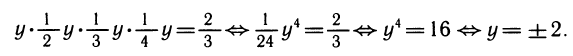
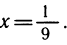
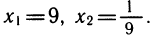
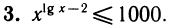
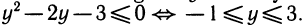
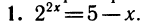
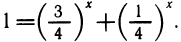
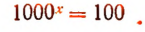
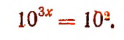

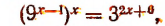

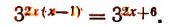
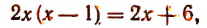
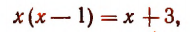
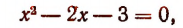
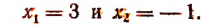
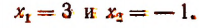
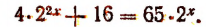
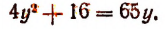
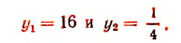
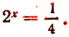
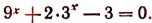
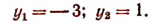
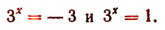
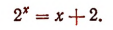
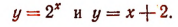
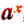 , где а>0, имеет при каждом действительном значении х одно и только одно действительное значение.
, где а>0, имеет при каждом действительном значении х одно и только одно действительное значение.