Реферат: Неравенства
| Название: Неравенства Раздел: Рефераты по математике Тип: реферат Добавлен 07:49:03 29 сентября 2010 Похожие работы Просмотров: 2003 Комментариев: 21 Оценило: 8 человек Средний балл: 4.1 Оценка: 4 Скачать | |||||||||||||
| Название | Показательные уравнения, неравенство и их системы |
| Анкор | Показательные уравнения, неравенства и их системы |
| Дата | 13.12.2020 |
| Размер | 293.54 Kb. |
| Формат файла |  |
| Имя файла | курсовая.docx |
| Тип | Реферат #160143 |
| Подборка по базе: Социальное неравенство.pptx, Бедность и неравенство.docx, 13-14 неравенство.docx, 0088 Генлерное неравенство в макроэкономике.doc Краевое государственное профессиональное образовательное автономное учреждение «Камчатский политехнический техникум» (КГПОАУ «Камчатский политехнический техникум») ИНДИВИДУАЛЬНЫЙ ПРОЕКТПо дсциплине ________________________________На тему: Показательные уравнения, неравенство и их системы. Студента (ки) ________ курса, группы _________ Имя _____________ Отчество _________________ _______ ________________ 20 ___ г. Петропавловск-Камчатский – 2020СОДЕРЖАНИЕ
ВВЕДЕНИЕ Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению показательных уравнений и неравенств . При решении показательных уравнений и неравенств часто возникают трудности, связанные со следующими особенностями: — при решении показательных уравнений и неравенств, ученики производят преобразования, которые не равносильны исходным уравнениям и неравенствам; — незнание четкого алгоритма решения показательных уравнений, неравенств и их систем; — при решении показательного уравнения и неравенства введением новой переменной забывают возвращаться к обратной замене. Вышесказанное определяет актуальность выбранной темы и полезность ее изучения для будущей педагогической практики. Цель данной работы: — изучить требования государственных стандартов по теме «Показательные уравнения и неравенства»; — проанализировать материал по теме в учебниках алгебры; — систематизировать методы решения показательных уравнений и неравенств. Объектом исследования является процесс обучения математике в старшей школе. Предметом исследования являются методические особенности изучения показательных уравнений, неравенств и их систем в старших классах средней школы. Практическая значимость исследования заключается в том, что разработанные методические рекомендации по изучению показательных уравнений и неравенств могут быть использованы учителями и практикантами в школе, а также в ходе занятий по элементарной математике на педагогическом отделении университета. Весь теоретический материал по теме «Показательные уравнения, неравенства и их системы» сгруппирован, разобраны алгоритмы решения и приведены примеры. Гипотеза исследования: учащиеся при решении различного рода задач получают первые навыки в исследовательской работе. У учащихся при этом развивается логическое мышление, повышается уровень математической культуры. А также развивают качества личности такие как: самостоятельность, целеустремленность, любознательность, интеллектуальное совершенствование. Задачи работы:
Методы исследования: анализ и обобщение специальной литературы по теме; сравнение. Теоретическая и практическая значимость исследования: данные материалы по показательным уравнениям, неравенствам и их систем, можно использовать, как в школе, так и для индивидуального обучения, при подготовке к сдаче ЕГЭ, а также для тех, кто хочет углубить свои знания по этой теме. Структура работы: состоит из трех глав, введения, заключения и списка литературы, и содержит 18 страниц. ГЛАВА 1 ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И ИХ МЕТОДЫ РЕШЕНИЯ Например: Простейшим показательным уравнением называется уравнение вида: 1) 2) 3) При решении показательных уравнений необходимо помнить, что решение любого показательного уравнения сводиться к решению простейших показательных уравнений. Методы решения показательных уравнений: — метод уравнивания показателей; — метод введения новой переменной; — метод вынесения общего множителя за скобки; — метод почленного деления; — метод группировки. Алгоритм решения уравнения методом уравнивания показателей [3].: — представить обе части показательного уравнения в виде степеней с одинаковыми основаниями; — на основании теоремы, если — решить полученное уравнение, согласно его виду (линейное, квадратное и т.д.). Задача. Решить уравнение: Решение: Представим 27 как Данное уравнение равносильно уравнению Ответ: Алгоритм решения показательного уравнения методом введения новой переменной: — определить возможность переписать данное уравнение в новом виде, позволяющем ввести новую переменную; — ввести новую переменную; — решить уравнение относительно новой переменной [4].. Задача. Решить уравнение: Решение: Пусть Найдем корни квадратного уравнения 1.3 Метод вынесения общего множителя за скобки Решение показательных уравнений методом вынесения общего множителя за скобки [1]. Задача. Решить уравнение: Т.к. Вынесем 27 представим, как Ответ: 3. Алгоритм решения показательного уравнения методом функционально-графическим методом: — левую и правую части уравнения представить в виде функций; — построить графики обеих функций в одной системе координат; — найти точки пересечения графиков, если они есть; — указать абсциссы точек пересечения, это корни уравнения. Задача: Решить уравнение: Строим таблицы значений: Таблица 1.
Таблица 2.
Построив графики этих функций, найдем абсциссу точки пересечения, она и будет корнем уравнения: График 1. Функций 1.5 Метод почленного деления Данный метод заключается в том, чтобы разделить каждый член уравнения содержащий степени с одинаковыми показателями, но разными основаниями, на одну из степеней. Этот метод применяется для решения однородных показательных уравнений. Задача. Решить уравнение: Решение: Разделим обе части уравнения почленно на Сделаем замену Ответ: 1.6 Метод группировки Способ группировки заключается в том, чтобы собрать степени с разными основаниями в разных частях уравнения, а затем разделить обе части уравнения на одну из степеней [6]. Задача. Решить уравнение: ГЛАВА 2 ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА И ИХ МЕТОДЫ РЕШЕНИЯ Решение показательных неравенств основано на строгой монотонности показательной функции. Известно, что o при основании, большем единицы, показательная функция возрастает, при положительном основании, меньшем единицы, показательная функция убывает [3]. Решение неравенств подобного вида основано на следующих утверждениях: При При Заметим, что применяя какой-либо метод при решении неравенства, содержащего знак «>», можно этот же метод применять и при решении неравенств, содержащих знаки « 0, тогда При решении неравенств подобного вида применяют логарифмирование обеих частей по основанию a или b. Учитывая свойства показательной функции, получаем: При При Чтобы пользоваться свойством монотонности показательной функции следует путем надлежащих преобразований добиться одинаковых оснований в левой и правой частях неравенства. Методы решения показательных неравенств: — Показательные неравенства, сводящиеся к простейшим — Однородные показательные неравенства — Показательные неравенства, сводящиеся к квадратным — Показательные неравенства, сводящиеся к рациональным — Неравенства, решаемые графическим методом Задача. Решить неравенство : Перепишем неравенство следующим образом: А далее вот так: Так как Ответ: 2.2 Решение неравенств, содержащих однородные функции относительно показательных функций Задание. Решить неравенство: Решение: Вынесем за скобку Тогда переходим к следующему неравенству (в силу того, что основание степени больше 1, знак неравенства не меняется): Ответ: Задание. Решить неравенство Разделим обе части неравенства на 3: Мы видим квадратное неравенство относительно Имеем: Ответ: 2.4 Решение неравенств, сводящиеся к рациональным Решить неравенство: Переносим все в левую сторону неравенства и приводим к общему знаменателю: Можно «отбросить» сумму Неравенство равносильно следующему: 2.5 Решение неравенств, решаемые графическим методом Решить неравенство: Рассмотрим функции А значит, если вернуться к неравенству и посмотреть на него с графической точки зрения, мы должны взять те значения Ответ: 3.1 Системы, содержащие одно или два показательных уравнений При решении систем уравнений, содержащих показательные функции, чаще всего используют традиционные методы решения систем уравнений: метод подстановки и метод замены переменных [8]. Множество упорядоченных пар, точек (в случае систем с тремя переменными) и т.д. значений переменных, обращающих в истинное равенство каждое уравнение системы, называется решением системы уравнений. Решить систему уравнений – значит найти все ее решения или доказать, что решений нет. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Система уравнений называется определенной, если она имеет конечное число решений, и неопределенной, если она имеет бесчисленное множество решений. Две системы называются равносильными, если они имеют одно и то же множество решений. 3.2 Системы неравенств. Совокупность неравенств Несколько неравенств с одной переменной образуют систему неравенств, если ставиться задача об отыскании всех тех значений переменной, которые удовлетворяют одновременно каждому из этих неравенств (т.е. если отыскиваются все общие решения исходных неравенств). Значение переменной, при котором каждое неравенство системы обращается в верное числовое неравенство, называется решением системы неравенств. Две системы неравенств называются равносильными, если они имеют общее множество решений, удовлетворяющих этим неравенствам [7]. Очевидно, что решением системы неравенств является пересечение решений неравенств, образующих систему, а решением совокупности неравенств является объединение решений неравенств, образующих совокупность. Несколько неравенств с одной переменной образуют совокупность неравенств, если ставится задача об отыскании всех тех значений переменной, каждое из которых удовлетворяет по крайней мере одному их этих неравенств. Подводя итоги данного исследования, можно сделать следующие выводы: 1. Показательные уравнения и неравенства представляют интерес для учащихся. При решении показательных уравнений и неравенств развиваются навыки систематизации, логического мышления при выборе правильного метода решения, повышает творческие и умственные способности. 2. Для решения каждого вида уравнений и неравенств в работе представлен наиболее удобный способ. Трудности могут возникнуть при решении систем, содержащие одно или два показательных уравнения, т.к. нужно правильно определить метод решения. В ходе исследования были решены следующие задачи: — подробно рассмотрен теоретический материал; — изучены различные методы решения показательных уравнений, неравенств и их систем (методы уравнивания показателей, введения новой переменной, функционально-графический, почленного деления, вынесения общего множителя за скобки, группировки). Реферат » Решение уравнений и неравенств графическим способом» ( 9 класс)Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. МБОУ Алтайская СОШ №1 Тема : « Графическое решение уравнений и неравенств» Учащаяся 9 а класса МБОУ Алтайская СОШ №1 Бабаева Галина Яковлевна, МБОУ Алтайской СОШ №1 С. Алтайское , Алтайский район, 2019 год. II . Основная часть 2. Как графически решить уравнение________________________стр.4 3. Какие бывают функции ?________________________________стр.4 4. Графическое решение линейного уравнения с одной переменной.стр.5 5. Решение квадратного уравнения графическим способом._____ стр6-8 6. Графическое решение смешанных уравнений._______________стр.8-12. 7. Решение квадратных неравенств графическим способом_______стр.13 8. Решение линейных неравенств графическим способом стр 14 IV . Список литературы______________________________________стр.16 Цель моей работы – изложить графический метод решения уравнений и неравенств, который дает возможность определить корни или доказать ,что уравнение корней не имеет ( или решением неравенства является пустое множество). Актуальность темы : графический метод, опирающийся на знания элементарных функций, удобно применять при решении задач на нахождение числа корней и на нахождение корней уравнений. Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес. В данной исследовательской работе я показала как наиболее удобным способом преобразовывать уравнения . чтобы сводить к построению элементарных функций. Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков не ограничивается только этим. В ряде случаев графики облегчают нахождение решений уравнений и неравенств, сокращая и упрощая аналитические выкладки, и часто при этом являются единственным методом решения таких задач. Данный метод может использоваться не только для одиночных уравнений, но и для их систем, а также неравенств Уравнение – выражение, содержащее переменную. Решить уравнение – это значит найти все его корни, или доказать, что их нет. Корень уравнения – это число, при подстановке которого в уравнение получается верное числовое равенство. График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргументов, а ординаты – соответствующим значениям функции. Решение уравнений графическим способом позволяет найти точное или приближенное значение корней, позволяет найти количество корней уравнения. При построении графиков и решении уравнений используются свойства функции, поэтому метод чаще называют функционально-графическим. Графиком функции y = f(x) называется множество всех точек Заметим , что так как функция f сопоставляет каждому x D(f) одно число f(x) , то график функции f пересекается любой прямой, параллельной оси ординат, не более, чем в одной точке. И наоборот: всякое непустое множество точек плоскости, имеющее со всякой прямой, параллельной оси ординат, не более одной общей точки, является графиком некоторой функции. Не всякое множество точек координатной плоскости является графиком какой-либо функции. Например, множество точек окружности не может быть графиком функции, поскольку значению абсциссы внутри окружности, соответствует два значения ординаты. В общем случае уравнение с одной переменой х можно записать в виде f(x)=g(x),где f(x) и g(x) — некоторые функции. Функция f(x) является левой частью , а g(x) — правой частью уравнения. Тогда для решения уравнения необходимо построить в одной системе координат графики функций f(x) и g(x). Абсциссы точек пересечения будут являться решениями данного уравнения. Использование монотонности функций при решении уравнений: если функция 2. Как графически решить уравнение. Иногда уравнения решают графическим способом. Для этого надо преобразовать уравнение так (если оно уже не представлено в преобразованном виде), чтобы слева и справа от знака равенства стояли выражения, для которых легко можно нарисовать графики функций. Графическим решением уравнения являются абсциссы точек пересечения графиков построенных функций. Графики могут пересекаться в нескольких точках, в одной точке, вообще не пересекаться. Отсюда следует, что уравнение может иметь несколько корней, или один корень, или вообще их не иметь. 3. Какие бывают функции . Линейная функция задаётся уравнением у = k*x+ b , где k и b – некоторые числа. Графиком этой функции является прямая. Для построения прямой достаточно в таблице значений взять только две точки. Это вытекает из аксиомы планиметрии Функция обратной пропорциональности у =k/x , где. График этой функции называется гиперболой. Функция (х– a)^2+ (у – b)^2 = r^2 , где а , b и r – некоторые числа. Это окружность радиуса r с центром в т. А ( а , b ). Квадратичная функция y = a *х 2 + b*x+ c , где а, b, с – некоторые числа и а не равно 0. Графиком этой функции является парабола. Графики линейных функций, содержащих выражение под знаком модуля. Для построения графиков функций, содержащих выражение под знаком модуля, сначала находят корни выражений, стоящих под знаком модуля. Эти корни разбивают числовую прямую на промежутки. График строят в каждом промежутке отдельно. В простейшем случает, когда только одно выражение стоит под знаком модуля и нет слагаемых без знака модуля, можно построить график функций, опустив знак модуля, а затем часть графика, расположенного в области отрицательных значений y , отобразить симметрично оси ОХ. Элементарная функций, содержащая модуль : 4. Графическое решение линейного уравнения с одной переменной. Как мы уже знаем, графиком линейного уравнения является прямая линия, отсюда и название данного вида. Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и уравнение решено. Мы нашли корень .А я покажу , как это сделать графическим способом. Задание . Решить графическим способом уравнение : 2 x − 10 = 2 1)Перенесем слагаемые следующим образом: 2 x = 12. 2) Построим графики функций: y=2x и y=12. Но можно решать и по-другому. Для рассмотрения альтернативного решения вернемся к нашему уравнению: Построим графики функций: y=2 x − 10 y =2 5. Решение квадратного уравнения графическим способом. Для этого преобразуем уравнение к виду: х 2 =-2x+8 . Построим графики функций: у = -2x+8 и у = х 2 Получим точки пересечения графиков данных функций. В ответ запишем абсциссы этих точек : x = -4 и x =2. Данное уравнение можно решить , переписав уравнение следующим образом: x^2 – 8 = -2x Тогда будем строить графики функций: y = x^2 – 8 и y = -2x. А также уравнение можно решить , переписав следующим образом: Тогда будем строить графики следующих функций : y = x^2 + 2x и y = 8 . При этом абсциссы точек пересечения графиков будут одинаковые : Задание. Решить уравнение: x² – 2x = 0 Перепишем уравнение в виде : x² = 2x Построим графики функций y = x² и y = 2 и найдем точки их пересечения : Задание. Решить уравнение: х 2 +2=0 Преобразуем так: х 2 = -2 Построим графики функций: у=-2 и у= х 2 Графики функций не пересекаются ,поэтому уравнение решений не имеет. Ответ : решений нет. 6. Графическое решение смешанных уравнений. Задание. Решить уравнение: 3/х +2 =х 1)Перенесем слагаемые таким образом: 3/ х = х-2 2) Построим графики функций от каждой части уравнения. Найдем координаты точек пересечения графиков данных функций. Из построения видно, что графики функций пересекаются в точках с координатами : (3;1) и(-1;-3). Задание. Решить уравнение: 2 х^3 – x — 1=0 Перепишем его так : 2 х 3 = x + 1 Построим графики функций от левой и правой части уравнения: у= 2 х 3 (графиком этой функции является кубическая парабола) и график от правой части уравнения :у=х+1 Из построения видно, что абсцисса точки пересечения является х=1. значит, в ответ нужно записать: х=1 Решим графическим способом такое уравнение : х 3 =8. Строим графики функций: у = х 3 и у=8., затем найдем абсциссу точки пересечения графиков этих функций. Задание. Решить уравнение: √x – 0.5x = 0 Перепишем так: √x = 0.5x Построим графики функций: у= 0.5x и у = √x Как видно из построения, графики функций пересекаются в двух точках: Нас интересует только координата x. Значит уравнение √x – 0.5x = 0 имеет два корня: x 1 = 0 и x 2 = 4. 7. Решение квадратных неравенств графическим способом. Способ , который нам хорошо известен при изучении данной темы по учебнику. Я же предлагаю переписать неравенство следующим образом : х^2-4>3х. Построим графики функций от левой и правой частей неравенства. Выделим ту часть, где график от левой части выше графика от правой части. На мой взгляд такое решение более красивое , интересное и более понятное. 8. Решение линейных неравенств и систем неравенств графическим способом. Называют ся линейными неравенствами . График линейного или квадратного неравенства строится так же, как строится график любой функции (уравнения). Разница заключается в том, что неравенство подразумевает наличие множества решений, поэтому график неравенства представляет собой не просто точку на числовой прямой или линию на координатной плоскости. С помощью математических операций и знака неравенства можно определить множество решений неравенства Вообще графический способ решения неравенств с одной переменной применяется не только для решения квадратных неравенств, но и неравенств других видов. Суть графического способа решения неравенств следующая: рассматривают функции y = f(x) и y = g(x) , которые соответствуют левой и правой частям неравенства, строят их графики в одной прямоугольной системе координат и выясняют, на каких промежутках график одной из них располагается ниже или выше другого. Те промежутки, на которых график функции у = f (х) выше графика функции y = g(х) являются решениями неравенства f(x)>g(x) ; график функции y = f(х) не ниже графика функции y = g(x) являются решениями неравенства f(x) ≥ g(x) ; график функции у = f (х) ниже графика функции y = g(х) являются решениями неравенства f(x) ; график функции y = f(х) не выше графика функции y = g(х) являются решениями неравенства f(x) ≤ g(x) . Также скажем, что абсциссы точек пересечения графиков функций y = f(x) и y = g(x) , являются решениями уравнения f(x) = g(x) . Мы рассмотрели графический метод решения уравнений и квадратных неравенств; рассмотрели конкретные примеры, при решении которых использовали некоторые свойства функций. Иногда при графическом решении некоторых уравнений и неравенств корни определяются только приближённо в силу того, что невозможно с высокой точностью построить график функции, измерить абсциссы или ординаты точек пересечения графика с осями координат или с другими графиками. Тем не менее, той точности, которую обеспечивает графический метод, бывает вполне достаточно для практических нужд. Построение графиков основывается на знании основных элементарных функций, и на основные методы построения графиков функций. В работе представлено достаточное количество примеров, раскрывающих графический метод решения линейных и квадратных уравнений и неравенств, который доступен для понимания . Работа может быть использована для углубления и расширения знаний в области построения графиков функций и использовании графического метода при решении некоторых видов уравнений и неравенств. Теорию можно использовать так же при подготовки к экзаменам , к олимпиадам. Я свою работу представляла учащимся 8-х и 9-х классов нашей школы. И продолжаю дополнять свои исследования , а именно находить красивые решения линейных неравенств и систем неравенств. Это и закрепление изученных свойств функций, и прекрасная демонстрация их применения на практике. В старших классах я буду ещё знакомиться с другими функциями , с другими уравнениями и неравенствами и м не интересно будет продолжить свой проект. источники: http://topuch.ru/pokazatelenie-uravneniya-neravenstvo-i-ih-sistemi/index.html http://infourok.ru/referat-reshenie-uravneniy-i-neravenstv-graficheskim-sposobom-klass-3684418.html |
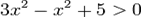 — алгебраическое, второй степени.
— алгебраическое, второй степени.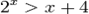 — трансцендентное.
— трансцендентное.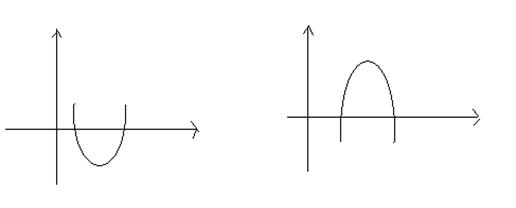
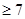 ;
;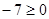 .
.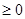 ;
;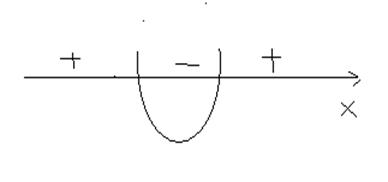
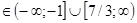 .
.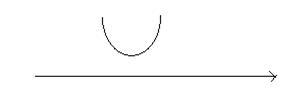
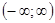 .
.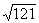 – 1 – 20 = – 10 2 +х-2
– 1 – 20 = – 10 2 +х-2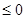
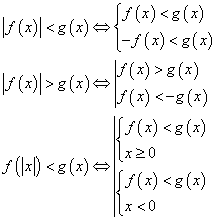
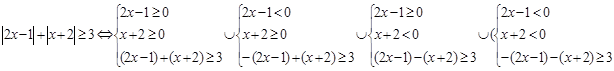 .
.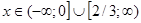 .
.

 ;
; ;
; .
. равносильно уравнению вида
равносильно уравнению вида  , приравнивнять показатели степеней;
, приравнивнять показатели степеней;
 . Данное показательное уравнение имеет одинаковое основание 3.
. Данное показательное уравнение имеет одинаковое основание 3.



 , получим квадратное уравнение:
, получим квадратное уравнение:
 — не удовлетворяет условию
— не удовлетворяет условию  .
.



 равносильно
равносильно  , запишем как:
, запишем как:
 :
:






 .
.


 , получим равносильное ему уравнение:
, получим равносильное ему уравнение:













 то неравенство
то неравенство  ;
;  , то неравенство
, то неравенство  при
при  равносильно числовому неравенству 1
равносильно числовому неравенству 1  при
при 

 ;
; .
.



 – возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:
– возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:

 .
. .
.






 .
. 



 которое будем решать методом интервалов.
которое будем решать методом интервалов.

 или
или 
 или
или 






 в силу ее положительности:
в силу ее положительности:









 и
и  . Обе они определены на
. Обе они определены на  . Первая – возрастает, вторая – убывает. Значит, уравнение
. Первая – возрастает, вторая – убывает. Значит, уравнение  имеет не более одного решения. Несложно заметить, что
имеет не более одного решения. Несложно заметить, что 
 , которые отвечают за ту часть графика
, которые отвечают за ту часть графика  , что лежит выше графика
, что лежит выше графика  , то есть
, то есть  .
. .
.  Напомним, что систему двух уравнений с двумя переменными обозначают фигурными скобками и обычно записывают в виде:
Напомним, что систему двух уравнений с двумя переменными обозначают фигурными скобками и обычно записывают в виде:


 строго возрастает, а функция
строго возрастает, а функция  строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение
строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение  на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем.
на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем.










 ,
, 