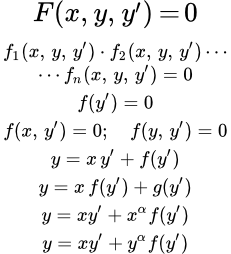Математика. Шпоры. Решение оду. Постановка задачи Коши для оду 1ого порядка разрешенных и неразрешенных относительно производной для норм систем оду и т д
| Название | Решение оду. Постановка задачи Коши для оду 1ого порядка разрешенных и неразрешенных относительно производной для норм систем оду и т д |
| Анкор | Математика. Шпоры.doc |
| Дата | 24.12.2017 |
| Размер | 0.93 Mb. |
| Формат файла |  |
| Имя файла | Математика. Шпоры.doc |
| Тип | Решение #12746 |
| Категория | Математика |
| страница | 1 из 4 |
Подборка по базе: Практическое занятие 6 РЕШЕНИЕ.docx, Задачи по римскому праву с решением.doc, 4 задачи.docx, Практические (ситуационные ) задачи.doc, Итоговое задание решение.docx, Ситуационные задачи хирургия.docx, Ишемический инсульт Неврология задачи.docx, Психология Задачи к семинарам.doc, 15 урок Решение задач.pptx, Вопросы и задачи УЧР 2021 год.odt
Решением ОДУ называется функция y(x), имеющая непрерывные производные нужного порядка, исходя из уравнений, при постановке которые уравнение превращается в точку. Решением дифференциального уравнения порядка n называется функция y(x) , имеющая на некотором интервале (a, b) производные y ‘( x ), y »( x ). y ( n ) ( x ) до порядка n включительно и удовлетворяющая этому уравнению. Частное решение диф.ур.-ф-ция превращающая ур.в подмножество. Общее решение-все множество частных результатов. Задача Коши-нахождение решения ДУ, удовлетворяющего начальным условиям. ОДУ первого порядка, разрешённое относительно производной Система n ОДУ первого порядка, разрешённая относительно производных (нормальная система n-го порядка) ОДУ n-го порядка, разрешённое относительно старшей производной | Общий вид ОДУ без выделения вектора произвольных постоянных C таков (см. п. 1.1.2):
Если (1) можно разрешить относительно старших производных, т. е. привести к виду
то путем увеличения числа неизвестных скалярных функций (см. п. 1.4.5) уравнение (2) всегда можно привести к нормальному виду
Поэтому в дальнейшем основным объектом изучения будет именно нормальная система (НС). Задача Коши, или начальная задача для уравнения (2) — это система, состоящая из (2) и начального условия
где t0 О R — начальный момент, y0 — начальное значение. Для (НС) начальное условие записывается в виде
Геометрический смысл задачи Коши (НС), (НУ) заключается в том, чтобы во множестве всех интегральных кривых системы (НС) найти ту, которая проходит через точку(t0, x0) (см. рис. 1). График решения ОДУ y=f(x) называется интегральной кривой ДУ. Нахождение множества решений ДУ называют интегрированием ДУ | ||||||
| 2)Уравнения с разделяющимися переменными. 1. Уравнения с разделёнными переменными. Так называются уравнения вида удовлетворяющее начальному условию
Пусть y(x) — решение этого уравнения, т.е. f(x)dx + g(y(x))dy(x) = 0. Интегрируя это тождество, получим 2. Так называются уравнения вида
Эти уравнения легко сводятся к уравнению с разделёнными переменными: Записываем уравнение (1) в форме Уравнение (2) делим на f2(x) g1(y): Эти уравнения — с разделёнными переменными. Интегрируя, получим общие интегралы:
В обоих случаях возможна потеря решений: деление на функцию может привести к уравнению, которое неэквивалентно данному. y = y3, …, очевидно, являются решениями исходного уравнения. В обоих случаях эти решения могут содержаться в общем решении, но могут и не содержаться в нём; последнее может случиться, если на этих решениях нарушаются условия теоремы существования и единственности решения задачи Коши. | 7)ОДУ высших порядков. Простейшие случаи, допускающие понижение порядка уравнения.. Дифференциальным уравнением порядка n называется уравнение вида: В некоторых случаях это уравнение можно разрешить относительно y ( n ) : Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений. Уравнения, допускающие понижение порядка. Понижение порядка диф ур-ния – основной метод решения ур-ний высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем ур-ниям. Рассмотрим случаи, когда возможно понижение порядка. Если f(x) – ф-ция непрерывная на некотором промежутке a 3.Линейное однородное уравнение первого порядка Общее решение: Линейное неоднородное уравнение первого порядка Метод Лагранжа (метод вариации произвольных постоянных)Постановка задачи. Найти решение задачи Коши для линейного неоднородного уравнения с постоянными коэффициентами
1. Записываем соответствующее однородное уравнение с постоянными коэффициентами
Находим фундаментальную систему решений и и общее решение однородного уравнения
2. Применяем метод Лагранжа (метод вариации произвольных постоянных). Если известна фундаментальная система решений и однородного уравнения (3), то общее решение соответствующего неоднородного уравнения (1) может быть найдено по формуле
где функции и определяются из системы линейных алгебраических уравнений |  (4) (4)Интегрируя, находим функции и и записываем общее решение неоднородного уравнения. 3. Используя начальные условия (2), находим решение задачи Коши Метод Бернулли. Одним из методов решения дифференциального уравнения Бернулли является сведение его к линейному неоднородному дифференциальному уравнению первого порядка введением новой переменной . Действительно, при такой замене имеем
После решения этого уравнения и проведения обратной замены получаем искомое решение. | |||||
| 4.Структура решения линейного неоднородного ОДУ. Теорема (о структуре общего решения неоднородного дифференциального уравнения). Общее решение неоднородного дифференциального уравнения есть сумма какого-либо его частного решения и общего решения соответствующего ему однородного уравнения: где – частное решение ДУ(1), y 0 – общее решение соответствующего однородного ДУ (2): y ( n ) + a 1 y ( n -1) + . +a n y = 0, Докажем теорему для уравнения второго порядка y // + py / + qy = f ( x ). (4) Рассмотрим соответствующее однородное ДУ: y // + py / + q = 0. (5) Обозначим y 1, y 2 его линейно независимые частные решения и y 0 = c 1 y 1 + c 2 y 2 – его общее решение.) Пусть – какое-то частное решение ДУ (4). Покажем, что решение (3) удовлетворяет ДУ (4). Подставим формулу (3) в ДУ (4) (предва-рительно найдём производные): Получаем тождественное равенство, так как первая скобка обращается в нуль в силу того, что y 0– общее решение однородного ДУ(5), а вторая скобка равна правой части, так как – частное решение ДУ (4). Теорема доказана. то |  5)Уравнение Бернулли, два метода его решения 5)Уравнение Бернулли, два метода его решенияЕсли α — действительное число, отличающееся от 0 и 1, т.к. при α=0 и α=1 ур-ние обращается в линейное. Данное ур-ние решается 2 способами: 1.Из него можно сделать линейное ур-ние, разделив : 2..Решать точно так же как и однородное ур-ние, поскольку левая часть у них одинаковая. | ||||||
| 6.Рассмотрим уравнение вида F ( x , y , y ‘ ) = 0 , не разрешённое относительно производной. Если попытаться выразить из него y ‘ , то можно получить , вообще говоря , несколько уравнений Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.Уравнения, не разрешённые относительно производной, выглядят так: Уравнения первого порядка n-ой степени решаются так: Если из уравнения Продифференцируем по x: Получили уравнение, разрешённое относительно производной. p(x,C) подставляем в (*), получим: Рассмотрим теперь случай, когда из уравнения Мы получили уравнение, разрешённое относительно производной Уравнение Лагранжа – это уравнение, линейное относительно x и y, оно имеет вид: Принцип решения: Вводим параметр Пусть Продифференцируем по x: Получили линейное уравнение первого порядка. Отсюда находим В итоге решение в параметрическом виде: Отдельно рассмотрим случай, когда Если это тождество, то есть Если это не тождество, а уравнение с корнями: например, p0 – корень, то есть Частный случай уравнения Лагранжа – это уравнение Клеро. Это когда уравнение Лагранжа имеет следующий вид: Общее решение уравнения Клеро: Здесь Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения. Простейшие ОДУ высших порядков, интегрируемые в квадратурах и допускающие понижение порядка. Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида F (x, y(x), y ‘(x), y »(x), … , y(n)(x)) = 0, где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения. Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество. Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме: y(n) = f(x, y, y ‘, y », … , y(n − 1)). Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия. Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x0) = y0, y ‘(x0) = y1, y »(x0) = y2, … , y(n − 1)(x0) = yn − 1. Общим решением дифференциального уравнения F(x, y(x), y ‘(x), y »(x), … , y(n )(x)) = 0 называется функция y = Ф(x, С1, С2, … , Сn), содержащая некоторые постоянные (параметры) С1, С2, … , Сn, и обладающая следующими свойствами: Ф(x, С1, С2, … , Сn) является решением уравнения при любых допустимых значениях С1, С2, … , Сm; для любых начальных данных y(x0) = y0, y ‘(x0) = y1, y »(x0) = y2, … , y(n − 1)(x0) = yn − 1, для которых задача Коши имеет единственное решение, существуют значения постоянных С1 = A1, С2 = A2, … , Сn = An, такие что решение y = Ф(x, A1, A2, …, An) удовлетворяет заданным начальным условиям. Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С1, С2, . Сn) = 0. Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения. Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок. Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y(n) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка. К уравнениям, допускающим понижение порядка, относятся в частности, уравнения, не содержащие искомой функции и ее производных до некоторого порядка, , т.е. уравнения вида Простейшее уравнение, допускающее понижение порядка — уравнение вида y(n) = f (x), его общее решение имеет вид К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие независимой переменной — уравнения вида F(y, y’, . y(n)) = 0. Порядок уравнения можно понизить заменив y ‘ = p(y). После подстановки получим дифференциальное уравнение относительно функции p = p(y) , в котором порядок старшей производной от p(y) будет на единицу меньше, чем порядок старшей производной от y(x) в исходном уравнении. К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие искомой функции — уравнения вида F(x, y’, . y(n)) = 0. Порядок уравнения можно понизить заменив y ‘ = p(x). После подстановки получим дифференциальное уравнение относительно функции p = p(x) на единицу меньшего порядка, чем исходное уравнение: F(x, p, p’, . p(n — 1)) = 0. Если правая часть уравнения F(x, y, y ‘. y(n) ) = 0, удовлетворяет условию однородностиF(x, ty, ty ‘. ty(n) ) = tk F(x, y, y ‘. y(n) ) то говорят, что это уравнение, однородное относительно неизвестной функции и всех ее производных. Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ‘. y(n) ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка. К уравнениям, допускающим понижение порядка, относятся уравнения, однородные относительно неизвестной функции и всех ее производных. Порядок такого уравнения можно понизить заменой Выражение для первой производной от y(x) не содержит производной от z(x): Поэтому, заменив в исходном уравнении y, y ‘. y(n) их выражениями через z(x), получим относительно z(x) дифференциальное уравнение на единицу меньшего порядка. Основные понятия, относящиеся к системам ОДУ: порядок системы, нормальная форма системы, общее и частное решения, общий и первый интегралы. Задача Коши для нормальной системы, её геометрический смысл. Совокупность соотношений вида: Где y1, y2, …, yn искомые функции от независимой переменной x, называется системой обыкновенных дифференциальных уравнений первого порядка. Будем предполагать функции F2, F2, …, Fn такими, что система разрешима относительно производных от искомых функций: Такие системы называются нормальными системами дифференциальных уравнений. Число уравнений, входящих в систему, называется порядком этой системы. Значит, наша система имеет n-ый порядок. Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной. Семейство решений системы (2), зависящее от n произвольных постоянных C1, C2, …, Cn называют обычно общим решением этой системы. Дадим определение общего решения системы (2) в области D изменения переменных x, y1, y2, …, yn. В качестве области D будем рассматривать область в пространстве (x, y1, y2, …, yn), в каждой точке которой имеет место существование и единственность решения задачи Коши для системы (2). Совокупность n функций (6), определённых в некоторой области изменения переменных x, C1, C2, …, Cn, имеющих непрерывные частные производные по x, будем называть общим решением системы (2) в области D, если система (6) разрешима относительно произвольных постоянных C1, C2, …, Cn в области D, так что при любых значениях x, y1, y2, …, yn, принадлежащих области D, системой (6) определяются значения C1, C2, …, Cn: и если совокупность n функций (6) является решением системы (2) при всех значениях произвольных постоянных C1, C2, …, Cn, доставляемых формулами (7), когда точка (x, y1, y2, …, yn) пробегает область D. Решение, получающееся из формулы общего решения при частных числовых значениях произвольных постоянных C1, C2, …, Cn,, включая бесконечности, будет частным решением. Решая задачу Коши при помощи формулы общего решения всегда получаем частное решение. 1-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), не приводящаяся к постоянной, называется интегралом системы (2), если при замене y1, …, yn любым частным решением этой системы она обращается в постоянную. 2-ое определение интеграла системы. Функция φ(x, y1, y2, …, yn), имеющая непрерывные частные производные по x, y2, …, yn, и такая, что в рассматриваемой области Равенство Совокупность n первых интегралов (7) обладает тем свойством, что она разрешима относительно искомых функций y1, y2, …, yn, причём в результате этого мы получаем общее решение (6) системы (2) в области D. Всякую совокупность n первых интегралов, обладающую таким свойством, будем называть общим интегралом системы (2) в области D. Фундаментальные системы решений нормальной системы однородных линейных ОДУ. Теорема существования фундаментальных систем. Теорема об общем решении (о структуре общего решения) нормальной системы однородных линейных ОДУ. Система обыкновенных дифференциальных уравнений вида: Будем искать решение Фундаментальной системой решений системы уравнений (*) называется системы из n линейно независимых вектор-функций. Теорема о структуре общего решения линейного однородного дифференциального уравнения. Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения: Теорема об общем решении (о структуре общего решения) нормальной системы неоднородных линейных ОДУ. Рассмотрим неоднородную линейную систему обыкновенных дифференциальных уравнений n-го порядка Здесь Справедлива следующая теорема о структуре общего решения этой неоднородной линейной системы ОДУ. Если матрица A(x) и вектор-функция b(x) непрерывны на [a, b], и пусть Φ(x) — фундаментальная матрица решений однородной линейной системы где C — произвольный постоянный вектор-столбец, x0 — произвольная фиксированная точка из отрезка [a, b]. Из приведенной формулы легко получить формулу решения задачи Коши для линейной неоднородной системы ОДУ — формулу Коши. Решением задачи Коши Метод вариации произвольных постоянных для отыскания частных решений нормальной системы неоднородных линейных ОДУ. Определение системы неоднородных линейных ОДУ. Система ОДУ вида: называется линейной неоднородной. Пусть Система (*) в векторно-матричном виде: Сам метод. Пусть имеется линейная неоднородная система (произвольный постоянный вектор, который получается в результате интегрирования, можно считать равным 0). Здесь точки x0, Видим, таким образом, что если в (3) в качестве C(t) брать Общее решение линейной неоднородной системы (1) может быть записано в виде Дифференциальные уравнения первого порядка, не разрешенные относительно производнойДифференциальные уравнения, которые удается разрешить относительно производнойСначала нужно проверить, не удастся ли уравнение решить относительно производной. Если уравнение удается разрешить относительно производной, то оно сводится к одному из ранее рассмотренных типов. ПримерРешить уравнение: Решим это уравнение относительно производной. Возводим уравнение (1) в квадрат: Интегрируем, применяя таблицу интегралов: Теперь объясним, как мы вынесли за знак логарифма в (3). Дифференциальные уравнения, допускающие разложение на множителиТакже нужно проверить, не удастся ли представить уравнение в виде произведения множителей: Виды не разрешенных уравнений, допускающих решениеДалее приведены виды не разрешенных относительно производной дифференциальных уравнений первого порядка, допускающих решение. Уравнения, не содержащие x и yЭто уравнения, которые не содержат в явном виде независимую и зависимую переменные: Уравнения, не содержащие x или yЭто уравнения, которые не содержат в явном виде либо независимую переменную , либо зависимую переменную : источники: http://helpiks.org/3-49185.html http://1cov-edu.ru/differentsialnye-uravneniya/pervogo-poryadka/ne-razreshennye/ |








 — общий интеграл (общее решение) этого уравнения.
— общий интеграл (общее решение) этого уравнения.  Исходное уравнение — с разделёнными переменными, интегрируя его, получим
Исходное уравнение — с разделёнными переменными, интегрируя его, получим  . Соотношение (x-1) 2 + y 3 = C — общее решение (общий интеграл) уравнения; для того, чтобы найти частное решение, удовлетворяющее начальному условию, надо подставить в общее решения данные значения x0 и y0, и найти значение постоянной C на этом решении: (2-1) 2 + 1 3 = 2
. Соотношение (x-1) 2 + y 3 = C — общее решение (общий интеграл) уравнения; для того, чтобы найти частное решение, удовлетворяющее начальному условию, надо подставить в общее решения данные значения x0 и y0, и найти значение постоянной C на этом решении: (2-1) 2 + 1 3 = 2  C = 2. Таким образом, решение поставленной задачи: (x-1) 2 + y 3 = 2.
C = 2. Таким образом, решение поставленной задачи: (x-1) 2 + y 3 = 2. или (1)
или (1) , затем делим на g(y) и умножаем на dx:
, затем делим на g(y) и умножаем на dx:  .
. .
. .
. .
. .
. .
.


 .
.




 (1)
(1) . (2)
. (2) . (3)
. (3) .
. ,
, . При n = 1 это дифференциальное уравнение становится уравнением с разделяющимися переменными
. При n = 1 это дифференциальное уравнение становится уравнением с разделяющимися переменными  .
. и дифференциальное уравнение Бернулли примет вид
и дифференциальное уравнение Бернулли примет вид .
.





 — решение уравнения
— решение уравнения














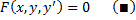 .
.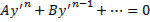
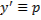
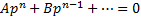
 y можно выразить, то есть
y можно выразить, то есть 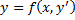 , то это решается методом введения параметра, а именно: Обозначим
, то это решается методом введения параметра, а именно: Обозначим 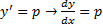 , получим:
, получим: 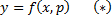
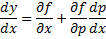
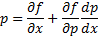
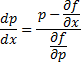
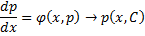
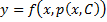 . Это и будет решение.
. Это и будет решение.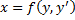 . Вводим параметр
. Вводим параметр 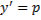 , получаем
, получаем 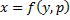 . Дифференцируем по y обе части:
. Дифференцируем по y обе части: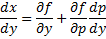
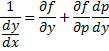
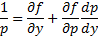
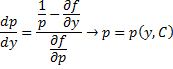
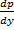 . В итоге получаем:
. В итоге получаем: 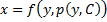 .
.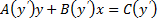 . Уравнения Лагранжа ВСЕГДА интегрируется в квадратурах.
. Уравнения Лагранжа ВСЕГДА интегрируется в квадратурах.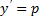 , получаем:
, получаем: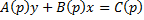
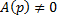 , поделим всё выражение на A(p):
, поделим всё выражение на A(p):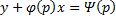

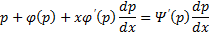
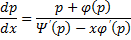


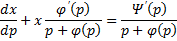
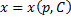 .
.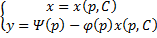
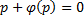 :
: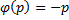 , то:
, то: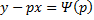
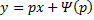
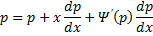
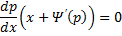
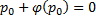 , тогда
, тогда 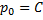 – решение.
– решение. 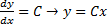
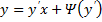 . Принцип решения: Вводим параметр
. Принцип решения: Вводим параметр 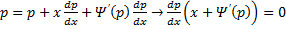

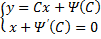
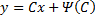 – семейство всевозможных кривых;
– семейство всевозможных кривых; 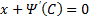 – огибающая этого семейства, тоже является решением и называется особое решение.
– огибающая этого семейства, тоже является решением и называется особое решение.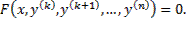 Заменой z(x) = y(k)(x) такое уравнение сводится к уравнению (n−k)–го порядка:
Заменой z(x) = y(k)(x) такое уравнение сводится к уравнению (n−k)–го порядка: 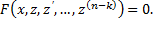 Если z = z(x,C1. Cn-k) решение этого уравнения, то общее решение уравнения n–го порядка может быть вычислено по формуле
Если z = z(x,C1. Cn-k) решение этого уравнения, то общее решение уравнения n–го порядка может быть вычислено по формуле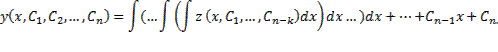
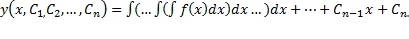

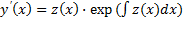 .
.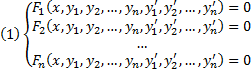
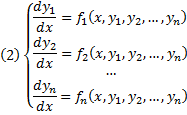
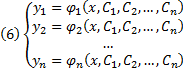
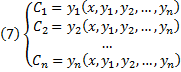
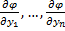 не обращаются одновременно в нуль, называется интегралом системы (2), если полный дифференциал этой функции обращается тождественно в нуль в силу системы (2), то есть имеет место тождество:
не обращаются одновременно в нуль, называется интегралом системы (2), если полный дифференциал этой функции обращается тождественно в нуль в силу системы (2), то есть имеет место тождество: .
.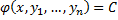 , где
, где 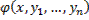 – интеграл системы (2) в смысле первого или второго определения, а C – произвольная постоянная, называется первым интегралом системы (2). Например, каждое из равенств (7) является первым интегралом системы (2).
– интеграл системы (2) в смысле первого или второго определения, а C – произвольная постоянная, называется первым интегралом системы (2). Например, каждое из равенств (7) является первым интегралом системы (2).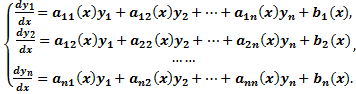 называется линейной системой. При
называется линейной системой. При 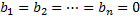 система становится однородной. В векторно-матричной форме:
система становится однородной. В векторно-матричной форме: 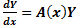 , где
, где 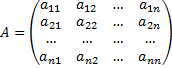 ,
, 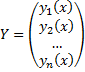
 . Ищем решение системы в таком виде:
. Ищем решение системы в таком виде:
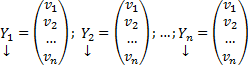
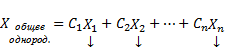 .
.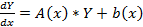
 A
A 
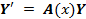 , то общее решение неоднородной системы Y’ = A(x)Y + b(x) имеет вид:
, то общее решение неоднородной системы Y’ = A(x)Y + b(x) имеет вид: 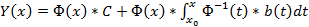
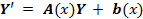 , Y(x0) = Y0 является вектор-функция
, Y(x0) = Y0 является вектор-функция 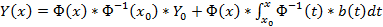
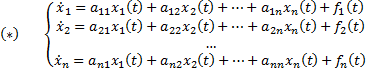
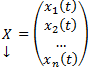
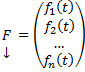
 .
.  — система однородная, иначе – неоднородная.
— система однородная, иначе – неоднородная.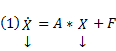 , тогда
, тогда 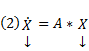 — линейная однородная система, соответствующая линейной неоднородной. Пусть
— линейная однородная система, соответствующая линейной неоднородной. Пусть 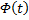 – фундаментальная матрица системы решений,
– фундаментальная матрица системы решений,  , где C – произвольный постоянный вектор, — общее решение системы. Станем искать решение
, где C – произвольный постоянный вектор, — общее решение системы. Станем искать решение 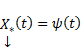 системы (1) в виде
системы (1) в виде 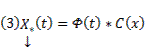 , где C(x) – неизвестная (пока) вектор-функция. Хотим, чтобы вектор-функция (3) была решением системы (1). Тогда должно быть справедливо тождество:
, где C(x) – неизвестная (пока) вектор-функция. Хотим, чтобы вектор-функция (3) была решением системы (1). Тогда должно быть справедливо тождество: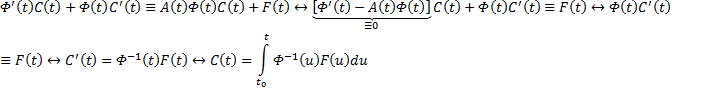
 – любые.
– любые.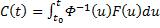 , то вектор-функция
, то вектор-функция 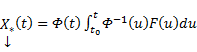 будет решением системы (1).
будет решением системы (1).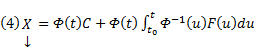 . Пусть требуется найти решение системы (1), удовлетворяющее начальному условию
. Пусть требуется найти решение системы (1), удовлетворяющее начальному условию  . Подстановка (4) начальных данных (5) даёт
. Подстановка (4) начальных данных (5) даёт 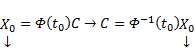 . Следовательно, решение задачи Коши (1)-(5) может быть записано в виде:
. Следовательно, решение задачи Коши (1)-(5) может быть записано в виде: 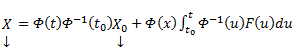 . В частном случае, когда
. В частном случае, когда 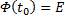 , последняя формула принимает вид:
, последняя формула принимает вид: 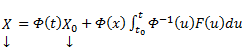 .
.