Уравнения параболического типа краевые задачи

Постановка задачи для уравнения параболического типа

Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). Как отмечалось выше, в одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид:

, 0 0 (15)

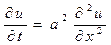
Уравнение (15), например, может описывать распространение тепла в тонком стержне длиной l, теплоизолированном по боковой поверхности. При этом функция u(x, t) задаёт значение температуры в любой точке стержня в произвольный момент времени t, при условии, что известно распределение температуры в стержне в начальный момент времени t = 0 и известна температура на концах стержня x = 0 и x = l в любой момент времени t. Таким образом, постановка задач для уравнения теплопроводности имеет следующий вид.

Первая начально-краевая задача. Если на границах стержня x = 0 и x = l заданы краевые условия первого рода, т.е. для любых моментов времени на концах стержня x = 0 и x = l заданы значения искомой функции u(x,t) (т.е. температуры):

и, кроме того, для функции u(x, t) заданы начальные условия, т.е. задано распределение температуры в любой точке стержня в момент времени t = 0:

то задачу (15) – (17) называют первой начально-краевой задачей для уравнения теплопроводности.

В терминах теории теплообмена функция u(x,t) описывает распределение температуры в пространственно-временной области W´T = <0 £ x £ l, 0 £ t £ T>, параметр а 2 – является коэффициентом температуропроводности, а краевые условия (16), (17) с помощью функций j ₁(t) и j ₂(t) задают температуру на границах
x = 0, x = l для различных моментов времени.

Вторая начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия второго рода, т.е. для x = 0 и x = l заданы значения производных искомой функции по пространственной переменной:

= j ₁(t), x = 0, t >0, (19)

= j ₂(t), x = l, t >0, (20)

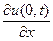
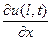
и, кроме того, для функции u(x, t) заданы начальные условия (21), то задачу (15), (19) – (21) называют второй начально-краевой задачей для уравнения теплопроводности. В терминах теории теплообмена граничные условия (19), (20) задают тепловые потоки на концах стрежня для различных моментов времени.

Третья начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия третьего рода, т.е. для x = 0 и x = l заданы линейные комбинации искомой функции и её частной производной по пространственной переменной:

+ a u(0, t) = j ₁(t), x = 0, t >0, (22)

+ b u(l, t) = j ₂(t), x = l, t >0, (23)

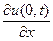
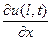
и, для функции u(x, t) заданы начальные условия (21), то задачу (15), (22), (23) называют третьей начально-краевой задачей для уравнения теплопроводности.

В терминах теории теплообмена граничные условия (22), (23) задают теплообмен между газообразной и жидкой средой (которые располагаются с разных «торцов» стержня) и границами расчётной области (т.е. внутренней частью стержня). Из-за теплообмена, температуры u(0, t) и u(l, t) на торцах стержня не известны, а известно, что температуры газообразной и жидкой среды соответственно равны
j ₁(t)/a и j ₂(t)/b. Параметры a и b являются коэффициентами теплообмена между газообразной или жидкой средой и соответствующей границей стержня.

Дата добавления: 2015-09-14 ; просмотров: 1247 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Применение дифференциального уравнения параболического типа для решения краевых задач динамической геодезии Текст научной статьи по специальности « Науки о Земле и смежные экологические науки»

Аннотация научной статьи по наукам о Земле и смежным экологическим наукам, автор научной работы — Канушин Вадим Федорович, Ганагина Ирина Геннадьевна

Рассматривается краевая задача с подвижной границей и динамическими граничными условиями, моделирующие кинематику с учетом динамики межфазового перехода и десорбционных процессов на поверхности.

Похожие темы научных работ по наукам о Земле и смежным экологическим наукам , автор научной работы — Канушин Вадим Федорович, Ганагина Ирина Геннадьевна

APPLICATION OF THE DIFFERENTIAL EQUATION OF PARABOLIC TYPE FOR THE SOLUTION OF REGIONAL PROBLEMS OF DYNAMIC GEODESY

The regional task with mobile border and the dynamic boundary conditions, modeling kinematics taking into account dynamics of interphase transition and stripping processes on a surface is considered.

Текст научной работы на тему «Применение дифференциального уравнения параболического типа для решения краевых задач динамической геодезии»

ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА ДЛЯ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДИНАМИЧЕСКОЙ ГЕОДЕЗИИ

Вадим Федорович Канушин

Сибирская государственная геодезическая академия, 630108, Россия, г. Новосибирск, ул. Плахотного, 10, к. т. н., доцент кафедры астрономии и гравиметрии, тел. (383-3)-61-01-59, е-mail: kaf.astronomy@ssga.ru

Ирина Геннадьевна Ганагина

Сибирская государственная геодезическая академия, 630108, Россия, г. Новосибирск, ул. Плахотного, 10, к. т. н., доцент кафедры астрономии и гравиметрии, тел. (383-3)-61-01-59, е-mail: kaf.astronomy@ssga.ru

Рассматривается краевая задача с подвижной границей и динамическими граничными условиями, моделирующие кинематику с учетом динамики межфазового перехода и десорб-ционных процессов на поверхности.

Ключевые слова: определения динамической составляющей гравитационного потенциала, краевые задачи динамической геодезии, дифференциальное уравнение параболического типа.

APPLICATION OF THE DIFFERENTIAL EQUATION OF PARABOLIC TYPE FOR THE SOLUTION OF REGIONAL PROBLEMS OF DYNAMIC GEODESY

Vadim F. Kanushin

The Siberian state geodetic academy, 630108, Russia, Novosibirsk, Plakhotnogo St., 10, to. so-called, associate professor of astronomy and gravimetriya, ph. (383-3)-61-01-59, e-mail: kaf. astronomy@ssga. ru

Irina G. Ganagina

The Siberian state geodetic academy, 630108, Russia, Novosibirsk, Plakhotnogo St., 10, to. so-called, associate professor of astronomy and gravimetriya, ph. (383-3)-61-01-59, e-mail: kaf. astronomy@ssga. ru

The regional task with mobile border and the dynamic boundary conditions, modeling kinematics taking into account dynamics of interphase transition and stripping processes on a surface is considered.

Key words: definitions of a dynamic component of gravitational potential, regional problems of dynamic geodesy, differential equation of parabolic type.

Природные геодинамические, а также техногенные явления по-разному влияют на результаты геодезических измерений, либо непосредственно через изменения положения пунктов на земной поверхности или опосредовано через временные изменения гравитационного поля, поскольку большинство геодезических измерений зависят от направления или модуля вектора силы тяжести. Кроме того системы координат, используемые для описания положения пунктов земной поверхности нестабильны: начала координат и направление осей земной системы координат изменяются в зависимости от действия эндогенных и экзогенных геодинамических процессов; таким образом, в координатах точек на земной поверхности проявляются дополнительные временные вариации.

Путём регистрации временных изменений результатов геодезических измерений можно исследовать пространственно-временную структуру геодина-мических процессов. Основным геодезическим вкладом в геодинамические ис-

следования является контроль в сфере мониторинга временных вариаций гравитационного поля и смещения пунктов на поверхности Земли относительно выбранной системы координат.

В принципе, строгий четырёхмерный подход к этой проблеме ведёт к постановке пространственно-временной краевой или начально-краевой задачи с зависящими от времени граничными данными, требующий описания всех динамических процессов, являющихся результатом антагонистического действия процессов двух видов, вызванных эндогенными и экзогенными силами.

Так как эти процессы крайне сложны и недостаточно изучены, то решение пространственно-временной задачи представляется далеко не простым и однозначным. Большинство предлагаемых в геодезической литературе [1, 2] подходов к решению этой задачи основаны на сведении четырёхмерной задачи к временной последовательности трёхмерных краевых задач. Допуская, что граничные данные в некоторую дискретную эпоху заданы на деформируемую краевую поверхность, ставится и решается обычная, не зависящая от времени краевая задача для любой эпохи, Такой конечно -разностный метод, в котором учитывается линейная аппроксимация кинематического поведения краевой поверхности, формально схож с классическими не зависящими от времени краевыми задачами. В зависимости от типа краевых данных и предположений относительно кинематического поведения краевой поверхности формулируются различные типы зависящих от времени краевых задач. Например, если известна геометрия краевой поверхности на любую эпоху, а неизвестным является изменение потенциала силы тяжести и его дериват, то возникает так называемая фиксированная краевая задача. Если временные вариации краевой поверхности неизвестны, а известны лишь на этой поверхности временные изменения гравитационного потенциала, а также модуль и направления силы тяжести, то возникает обратная краевая задача динамической геодезии со свободной краевой поверхностью. Эта поверхность изменяет свою форму и положение в пространстве (Х,У,7) со временем 1

Каждому моменту 1 в трёхмерном пространстве (Х,У,7) соответствует своя поверхность . Пусть две поверхности 80(Х,У,7,1;0) и Б^ХД^,^) согласованы

между собой тем, что любая точка Р0 е Б0 (Х,У,7,1;0) связана с точкой Р1 е Б1 (Х,У,2,1^). И пусть в результате геодинамических процессов масса перераспределится так, что ни геометрия поверхностей Б0 и 81, ни потенциалы силы тяжести ‘0 и ‘1 в точках Р0 и Р1, отнесённые к эпохам ^ и ^ не совпадают. Разность между геоцентрическими радиусами-векторами г0 = Ор и Г = Ор представляет собой вектор смещения (рис. 1).

8г(Рх -^,^ -,о) = гх(Ръ,1)- ro(P0,,0)

Рис. 1. Определение вектора смещения 5г = Р0Рі

Этот вектор можно записать в виде

Разность между значениями потенциалов ‘0 и ‘1 в точках Р0(Х,У,7) и

и(Д -Р0,Ч -^o) = ЩЦ,?1)-№0(Г0,10) (4)

— временная вариация потенциала силы тяжести.

Так как вектор силы тяжести равен

= ё1(Ръ 1- ёор ^ = ёаи (6)

— разность временной вариации силы тяжести.

Если разности и и 5g получены из повторного нивелирования и гравиметрических измерений в точках Р0 е (Х,У,7,1;0) и Р1 е (Х,У,7,^) и отнесены к поверхности 80(Х,У,7,1;0), то, возможно, вследствие малости этих величин в сравнении с абсолютными координатами и параметрами гравитационного поля

возникает зависимая от времени обратная краевая задача динамической геоде-

зии со свободной границей для определения вектора смещения 5 г и изменения потенциала силы тяжести И во внешнем пространстве по граничным условиям И(Р0,1;0) и 5g (Р0,1:0) на поверхности 80(Х,У,7Д0).

Эта задача имеет внешнее сходство с краевой геодезической задачей М. С. Молоденского [1, 3].

Таким образом, разнообразие формулировок, зависящей от времени обратной краевой задачи обусловлено тем, что в настоящее время ещё не разработана общая концепция решения задач динамической геодезии.

В лаборатории физической геодезии кафедры астрономии и гравиметрии СГГА для решения дифференциальных уравнений динамической геодезии разработано несколько методов их численного решения на ЭВМ 5.

В данной работе рассматривается один из методов составления и решения дифференциального уравнения параболического типа для определения динамической составляющей гравитационного потенциала.

Пусть функция U(M,t) = U(X1,X2,X3,t) — динамическая составляющая потенциала силы тяжести, которая в каждой фиксированной точке пространства (X1,X2,X3) изменяет свое значение с течением времени.

Пусть at изменение уровенной поверхности, соответствующее функции U(M,t) = a(t) и n (t) — вектор внешней нормали к этой поверхности с направляющими косинусами cos(«,X1), cos(n,X2), cos(n,X3).

“Я cos(n’ X1 ) + ^ cos(n’ X2 )+JU cos(n> X3 ) da = -jj gradUnda (7)

— является потоком вектора grad Un, через поверхность a, в направлении, противоположном вектору n в момент t.

За промежуток времени dt поток вектора grad Un через поверхность at будет равен

K = -dt Ц grad Unda, (8)

или применяя к формуле (8) теорему Гаусса-Остроградского [1] получим:

K = -dt Ц grad Unda = -dtjjj div grad Undr (9)

где xt — объем тела, ограниченного поверхностью at.

Такое же количество силовых линий поля grad Un за промежуток времени dt можно получить по формуле:

Приравнивая правые части формул (9) и (10), будем иметь:

dr = jjj div grad Undr . (11)

При произвольном объеме должно иметь место соотношение:

jjj fdU — div grad Un dr = 0, (12)

откуда получим дифференциальное уравнение эволюционного (параболического) типа [2]:

div grad Un = 0. (13)

Метод конечных разностей, аппроксимирующий дифференциальное уравнение (13), в котором используется метод дробных шагов, разработанный в работе [8], позволяет обеспечить наилучшие соотношения скорости, точности полученного решения и простоты реализации вычислительного алгоритма.

1. Постановка проблемы динамической геодезии, как решение геодезической краевой задачи М.С. Молоденского с краевыми условиями и граничной поверхностью, изменяющимися во времени. Отчет о НИР (промежуточный), руководитель Бузук В.В. N ГР.0196.00012360, №b.N 02. 97.0005664, СГГА. — Новосибирск. -1997. — 49с.

2. Неск В. Time — Dependent Geodetic Boundary Value Problems. Proc. Int.Symp. Figure and Dynamiok of the Earth, Moon, and Planets Pra gue. — 1988. — p. 195-225.

3. Молоденский, М.С. Методы изучения внешнего гравитационного поля и фигуры Земли // М.С. Молоденский, В.Ф. Еримеев, М.И. Юркина // Труды ЦНИИГАиК, вып. 131. — 1960. — 251 с.

4. Современные проблемы физической геодезии: учебно-методич. пособие по выполнению курсовой работы / И.Г. Ганагина, В.Ф., Канушин, Д.Н. Голдобин. — Новосибирск: СГГА, 2012. — 76 с.

5. Канушин В.Ф., Ганагина И.Г., Голдобин Д.Н. Определение когерентных составляющих физических полей Земли в представлении рядами Фурье // ГЕО-Сибирь-2008. IV Междунар. науч. конгр. : сб. материалов в 5 т. (Новосибирск, 22-24 апреля 2008 г.). — Новосибирск: СГГА, 2008. Т. 1. — С. 37-41.

6. Канушин В.Ф., Вахрушев А.Г., Румянцева Е.Д. Решение краевой задачи типа Дирихле с помощью вевлет-анализа // ГЕО-Сибирь-2011. VII Междунар. науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2011 г.). — Новосибирск: СГГА, 2011. Т. 1, ч. 1. — С. 173-177.

7. Канушин, В.Ф. Применение метода вириала для решения задач динамической геодезии // ГЕО-Сибирь-2011. VII Междунар. науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2011 г.). — Новосибирск: СГГА, 2011. Т. 1, ч. 1. — С. 182-185.

8. Бузук, В.В. О применении метода конечных разностей для решения краевых задач динамической геодезии / В.В. Бузук, В.Ф. Канушин, А. C. Горбунов // Тез. докл. 50 НТК преподават. СГГА, -Новосибирск. — 2000. — С. 34-35.

9. Ганагина И.Г., Канушин В.Ф. Анализ изменений гравитационного поля и высот квазигеоида, обусловленных сейсмической активностью // Интерэкспо ГЕО-Сибирь-2012. VIII Междунар. науч. конгр. : Междунар. науч. конф. «Геодезия, геоинформатика, картография, маркшейдерия» : сб. материалов в 3 т. (Новосибирск, 10-20 апреля 2012 г.). — Новосибирск: СГГА, 2012. Т. 3. — С. 8-13.

10. Исследование динамики физической поверхности и гравитационного поля Земли, обусловленных производством горных выработок на Малевском месторождении / В.Ф. Канушин, И.Г. Ганагина, Д.Н. Голдобин, И.А. Басова // Интерэкспо ГЕО-Сибирь-2012. VIII Междунар. науч. конгр. : Междунар. науч. конф. «Геодезия, геоинформатика, картография, маркшейдерия» : сб. материалов в 3 т. (Новосибирск, 10-20 апреля 2012 г.). — Новосибирск: СГГА, 2012. Т. 3. — С. 14-18.

11. Канушин В.Ф., Ганагина И.Г., Голдобин Д.Н. Моделирование аномального гравитационного поля в арктическом бассейне // ГЕО-Сибирь-2011. VII Междунар. науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2011 г.). — Новосибирск: СГГА, 2011. Т. 1, ч. 1. — С. 178-181.

12. Канушин В.Ф. Применение интегральных уравнений типа Вольтерра для решения задач динамической геодезии // Интерэкспо ГЕО-Сибирь-2012. VIII Междунар. науч. конгр. : Междунар. науч. конф. «Геодезия, геоинформатика, картография, маркшейдерия» : сб. материалов в 3 т. (Новосибирск, 10-20 апреля 2012 г.). — Новосибирск: СГГА, 2012. Т. 3. — С. 19-24.

Курсовая работа: Решение параболических уравнений

Реферат

В курсовой работе рассматривается метод сеток решения параболических уравнений. Теоретическая часть включает описание общих принципов метода, его применение к решению параболических уравнений, исследование разрешимости получаемой системы разностных уравнений. В практической части разрабатывается программа для численного решения поставленной задачи. В приложении представлен текст программы и результаты выполнения тестовых расчетов.

Объем курсовой работы: 33 с.

Ключевые слова: параболическое уравнение, уравнение теплопроводности, метод сеток, краевая задача, конечные разности.

1. Теоретическая часть

1.1 Метод сеток решения уравнений параболического типа

1.2 Метод прогонки решения разностной задачи для уравненийпараболического типа

1.3 Оценка погрешности и сходимость метода сеток

1.4 Доказательство устойчивости разностной схемы

2. Реализация метода

2.1 Разработка программного модуля

2.2 Описание логики программного модуля

2.3 Пример работы программы

К дифференциальным уравнениям с частными производными приходим при решении самых разнообразных задач. Например, при помощи дифференциальных уравнений с частными производными можно решать задачи теплопроводности, диффузии, многих физических и химических процессов.

Как правило, найти точное решение этих уравнений не удается, поэтому наиболее широкое применение получили приближенные методы их решения. В данной работе ограничимся рассмотрением дифференциальных уравнений с частными производными второго порядка, а точнее дифференциальными уравнениями с частными производными второго порядка параболического типа, когда эти уравнения являются линейными, а искомая функция зависит от двух переменных. В общем случае такое уравнение записывается следующим образом:

.

Заметим, что численными методами приходится решать и нелинейные уравнения, но находить их решение много труднее, чем решение линейных уравнений.

введем в рассмотрение величину . В том случае, когда уравнение называется параболическим. В случае, когда величина не сохраняет знак, имеем смешанный тип дифференциального уравнения. Следует отметить, что в дифференциальном уравнении все функции являются известными, и они определены в области , в которой мы ищем решение.

1. Теоретическая часть

1.1 Метод сеток решения уравнений параболического типа

Для решения дифференциальных уравнений параболического типа существует несколько методов их численного решения на ЭВМ, однако особое положение занимает метод сеток, так как он обеспечивает наилучшие соотношения скорости, точности полученного решения и простоты реализации вычислительного алгоритма. Метод сеток еще называют методом конечных разностей.Пусть дано дифференциальное уравнение

. (1.1)

Требуется найти функцию в области с границей при заданных краевых условиях. Согласно методу сеток в плоской области строится сеточная область , состоящая из одинаковых ячеек. При этом область должна как можно лучше приближать область . Сеточная область (то есть сетка) состоит из изолированных точек, которые называются узлами сетки. Число узлов будет характеризоваться основными размерами сетки : чем меньше , тем больше узлов содержит сетка. Узел сетки называется внутренним, если он принадлежит области , а все соседние узлы принадлежат сетке . В противном случае он называется граничным. Совокупность граничных узлов образует границу сеточной области .

Сетка может состоять из клеток разной конфигурации: квадратных, прямоугольных, треугольных и других. После построения сетки исходное дифференциальное уравнение заменяется разностным уравнением во всех внутренних узлах сетки. Затем на основании граничных условий устанавливаются значения искомого решения в граничных узлах. Присоединяя граничные условия сеточной задачи к разностным уравнениям, записанных для внутренних узлов, получаем систему уравнений, из которой определяем значения искомого решения во всех узлах сетки.

Замена дифференциального уравнения разностным может быть осуществлена разными способами. Один из способов аппроксимации состоит в том, что производные, входящие в дифференциальное уравнение, заменяются линейными комбинациями значений функции в узлах сетки по тем или иным формулам численного дифференцирования. Различные формулы численного дифференцирования имеют разную точность, поэтому от выбора формул аппроксимации зависит качество аппроксимации дифференциального уравнения разностным уравнением.

Рассмотрим неоднородное уравнение теплопроводности, являющееся частным случаем уравнений параболического типа:

, (1.2)

– известная функция.

Будем искать решение этого уравнения в области

Заметим, что эту полуполосу всегда можно привести к полуполосе, когда . Уравнение (1.2) будем решать с начальными условиями:

, (1.3)

– известная функция, и краевыми условиями:

(1.4)

где – известные функции переменной .

Для решения задачи область покроем сеткой .

Узлы сетки, лежащие на прямых , и будут граничными. Все остальные узлы будут внутренними. Для каждого внутреннего узла дифференциальное уравнения (1.2) заменим разностным. При этом для производной воспользуемся следующей формулой:

.

Для производной запишем следующие формулы:

,

,

.

Можем получить три вида разностных уравнений:

, (1.5)

, (1.6)

, (1.7)

.

Разностные уравнения (1.5) аппроксимируют уравнение (1.2) с погрешностью , уравнение (1.6) – с такой же погрешностью, а уравнение (1.7) уже аппроксимирует уравнение (1.2) с погрешностью .

В разностной схеме (1.5) задействованы 4 узла. Конфигурация схемы (1.5) имеет вид:

В схеме (1.6) также участвуют 4 узла, и эта схема имеет вид:

В схеме (1.7) участвуют 5 узлов, и эта схема имеет вид:

Первая и третья схемы – явные, вторая схема неявная. В случае явных схем значения функции в узле очередного слоя можно найти, зная значения в узлах предыдущих слоев. В случае неявных схем для нахождения значений решения в узлах очередного слоя приходится решать систему уравнений.

Для узлов начального (нулевого) слоя значения решения выписываются с помощью начального условия (1.3):

(1.8)

Для граничных узлов, лежащих на прямых и , заменив производные по формулам численного дифференцирования, получаем из граничных условий (1.4) следующие уравнения:

(1.9)

Уравнения (1.9) аппроксимируют граничные условия (1.4) с погрешностью , так как используем односторонние формулы численного дифференцирования. Погрешность аппроксимации можно понизить, если использовать более точные односторонние (с тремя узлами) формулы численного дифференцирования.

Присоединяя к системе разностных уравнений, записанных для внутренних узлов, начальные и граничные условия (1.8) и (1.9) для разностной задачи получим полные разностные схемы трех видов. Для проведения вычислений самой простой схемой оказывается первая: достаточно на основании начального условия найти значения функции в узлах слоя , чтобы в дальнейшем последовательно определять значения решения в узлах слоев и т.д.

Третья схема также весьма проста для проведения вычислений, но при ее использовании необходимо кроме значений решения в узлах слоя найти каким-то образом значения функции и в слое . Далее вычислительный процесс легко организовывается. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи.

С точки зрения точечной аппроксимации третья схема самая точная.

Введем в рассмотрение параметр . Тогда наши разностные схемы можно переписать, вводя указанный параметр. При этом самый простой их вид будет при .

В любом случае согласно методу сеток будем иметь столько уравнений, сколько имеется неизвестных (значения искомой функции в узлах). Число неизвестных равно числу всех узлов сетки. Решая систему уравнений, получаем решение поставленной задачи.

Разрешимость этой системы для явных схем вопросов не вызывает, так как все действия выполняются в явно определенной последовательности. В случае неявных схем разрешимость системы следует исследовать в каждом конкретном случае. Важным вопросом является вопрос о том, на сколько найденные решения хорошо (адекватно) отражают точные решения, и можно ли неограниченно сгущая сетку (уменьшая шаг по осям) получить приближенные решения, сколь угодно близкие к точным решениям? Это вопрос о сходимости метода сеток.

На практике следует применять сходящиеся разностные схемы, причем только те из них, которые являются устойчивыми, то есть при использовании которых небольшие ошибки в начальных или промежуточных результатах не приводят к большим отклонениям от точного решения. Всегда следует использовать устойчивые разностные схемы, проводя соответствующие исследования на устойчивость.

Первая из построенных выше разностных схем в случае первой краевой задачи будет устойчивой при . Вторая схема устойчива при всех значениях величины . Третья схема неустойчива для любых , что сводит на нет все ее преимущества и делает невозможной к применению на ЭВМ.

Явные схемы просты для организации вычислительного процесса, но имеют один весьма весомый недостаток: для их устойчивости приходится накладывать сильные ограничения на сетку. Неявные схемы свободны от этого недостатка, но есть другая трудность – надо решать системы уравнений большой размерности, что на практике при нахождении решения сложных уравнений в протяженной области с высокой степенью точности может потребовать больших объемов памяти ЭВМ и времени на ожидание конечного результата. К счастью, прогресс не стоит на месте и уже сейчас мощности современных ЭВМ вполне достаточно для решения поставленных перед ними задач.

1.2 Метод прогонки решения разностной задачи для уравнений параболического типа

Рассмотрим частный случай задачи, поставленной в предыдущем разделе. В области

найти решение уравнения

(1.10)

с граничными условиями

(1.11)

и начальным условием

. (1.12)

Рассмотрим устойчивую вычислительную схему, для которой величина не является ограниченной сверху, а, значит, шаг по оси и может быть выбран достаточно крупным. Покроем область сеткой

Запишем разностное уравнение, аппроксимирующее дифференциальное уравнение (1.10) во всех внутренних узлах слоя . При этом будем использовать следующие формулы:

,

.

Эти формулы имеет погрешность . В результате уравнение (1.10) заменяется разностным:

(1.13)

Перепишем (1.13) в виде:

. (1.14)

Данная вычислительная схема имеет следующую конфигурацию:

(1.15)

(1.16)

Система (1.14) – (1.16) представляет собой разностную задачу, соответствующую краевой задаче (1.10) – (1.12).

За величину мы положили .

(1.14) – (1.16) есть система линейных алгебраических уравнений с 3-диагональной матрицей, поэтому ее резонно решать методом прогонки, так как он в несколько раз превосходит по скорости метод Гаусса.

. (1.17)

Здесь , – некоторые коэффициенты, подлежащие определению. Заменив в (1.17) на будем иметь:

. (1.18)

Подставив уравнение (1.18) в (1.14) получим:

. (1.19)

Сравнив (1.17) и (1.19) найдем, что:

(1.20)

Положим в (1.14) и найдем из него :

,

.

(1.21)

Заметим, что во второй формуле (1.21) величина подлежит замене на согласно первому условию (1.15).

С помощью формул (1.21) и (1.20) проводим прогонку в прямом направлении. В результате находим величины

Затем осуществляем обратный ход. При этом воспользуемся второй из формул (1.15) и формулой (1.17). Получим следующую цепочку формул:

(1.22)

Таким образом, отправляясь от начального слоя , на котором известно решение, мы последовательно можем найти значения искомого решения во всех узлах стеки.

Итак, мы построили неявную схему решения дифференциальных уравнений параболического типа методом сеток.

1.3 Оценка погрешности и сходимость метода сеток

При решении задачи методом сеток мы допускаем погрешность, состоящую из погрешности метода и вычислительной погрешности.

Погрешность метода – это та погрешность, которая возникает в результате замены дифференциального уравнения разностным, а также погрешность, возникающая за счет сноса граничных условий с на .

Вычислительная погрешность – это погрешность, возникающая при решении системы разностных уравнений, за счет практически неизбежных машинных округлений.

Существуют специальные оценки погрешности для решения задач методом сеток. Однако эти оценки содержат максимумы модулей производных искомого решения, поэтому пользоваться ими крайне неудобно, однако эти теоретические оценки хороши тем, что из них видно: если неограниченно измельчать сетку, то последовательность решений будет сходиться равномерно к точному решению. Здесь мы столкнулись с проблемой сходимости метода сеток. При использовании метода сеток мы должны быть уверены, что, неограниченно сгущая сетку, можем получить решение, сколь угодно близкое к точному.

Итак, на примере решения краевой задачи для дифференциального уравнения параболического типа рассмотрим основные принципы метода сеток. Отметим, что если при решении разностной задачи небольшие ошибки в начальных и краевых условиях (или в промежуточных результатах) не могут привести к большим отклонениям искомого решения, то говорят, что задача поставлена корректно в смысле устойчивости по входным данным. Разностную схему называют устойчивой, если вычислительная погрешность неограниченно не возрастает. В противном случае схема называется неустойчивой.

1.4 Доказательство устойчивости разностной схемы

Пусть есть решение уравнения (1.14), удовлетворяющее возмущенным начальным условиям

и граничным условиям

.

Здесь – некоторые начальные ошибки.

.

Погрешность будет удовлетворять уравнению

(1.23)

(в силу линейности уравнения (1.14)), а также следующими граничными и начальными условиями:

, (1.24)

. (1.25)

Частное решение уравнения (1.23) будем искать в виде

. (1.26)

Здесь числа и следует подобрать так, чтобы выражение (1.26) удовлетворяло уравнению (1.23) и граничным условиям (1.24).

При целом удовлетворяет уравнению (1.23) и условиям (1.24).

Подставим уравнение (1.26) в уравнение (1.24). При этом получим:

.

Выражение в квадратных скобках равно

.

Подставляя это выражение в предыдущее уравнение вместо выражения в квадратных скобках и проводя сокращения на получим:

,

откуда находим :

.

Таким образом, согласно уравнению (1.26), получаем линейно-независимые решения уравнения (1.23) в виде

Заметим, что это частное решение удовлетворяет однородным краевым условиям (1.24). Линейная комбинация этих частных решений также является решением уравнения (1.23):

, (1.27)

причем , определенное в выражении (1.27), удовлетворяет для любых однородным граничным условиям (1.24). Коэффициенты подбираются исходя из того, что должны удовлетворять начальным условиям (1.25):

.

В результате получаем систему уравнений

,

содержащую уравнений с неизвестными . Решая построенную систему определяем неизвестные коэффициенты .

Для устойчивости исследуемой разностной схемы необходимо, чтобы при любых значениях коэффициентов , определяемое формулой (1.27), оставалось ограниченной величиной при . Для этого достаточно, чтобы для всех выполнялось неравенство

. (1.28)

Анализируя (1.28) видим, что это неравенство выполняется для любых значений параметра . При этом при или в крайнем случае, когда

,

остается ограниченным и при фиксированном не возрастает по модулю. Следовательно мы доказали, что рассматриваемая разностная схема устойчива для любых значений параметра .

2. Реализация метода

2.1 Разработка программного модуля

Поставлена цель: разработать программный продукт для нахождения приближенного решения параболического уравнения:

(1.29)

,

(1.30)

Разобьем область прямыми

– шаг по оси ,

– шаг по оси .

Заменив в каждом узле производные конечно-разностными отношениями по неявной схеме, получим систему вида:

. (1.31)

Преобразовав ее, получим:

, (1.32)

В граничных узлах

(1.33)

В начальный момент

. (1.34)

Эта разностная схема устойчива при любом . Будем решать систему уравнений (1.32), (1.33) и (1.34) методом прогонки. Для этого ищем значения функции в узле в виде

, (1.35)

где – пока неизвестные коэффициенты.

. (1.36)

Подставив значение (1.35) в (1.32) получим:

.

. (1.37)

Из сравнения (1.35) и (1.37) видно, что

. (1.38)

. (1.39)

Для из (1.32) имеем:

.

.

Откуда, используя (1.35), получим:

, (1.40)

. (1.41)

Используя данный метод, мы все вычисления проведем в следующем порядке для всех .

1) Зная значения функции на границе (1.33), найдем значения коэффициентов по (1.40) и по (1.38) для всех .

2) Найдем по (1.41), используя для начальное условие (1.34).

3) Найдем по формулам (1.39) для .

4) Найдем значения искомой функции на слое, начиная с :

2.2 Описание логики программного модуля

Листинг программы приведен в приложении 1. Ниже будут описаны функции программного модуля и их назначение.

Функция main() является базовой. Она реализует алгоритм метода сеток, описанного в предыдущих разделах работы.

Функция f (x, y) представляет собой свободную функцию двух переменных дифференциального уравнения (1.29). В качестве аргумента в нее передаются два вещественных числа с плавающей точкой типа float. На выходе функция возвращает значение функции , вычисленное в точке .

Функции mu_1 (t) и mu_2 (t) представляют собой краевые условия. В них передается по одному аргументу (t) вещественного типа (float).

Функция phi() является ответственной за начальный условия.

В функции main() определены следующие константы:

– правая граница по для области ;

– правая граница по для области ;

– шаг сетки по оси ;

– шаг сетки по оси ;

Варьируя и можно изменять точность полученного решения от менее точного к более точному. Выше было доказано, что используемая вычислительная схема устойчива для любых комбинаций параметров и , поэтому при устремлении их к нуля можем получить сколь угодно близкое к точному решение.

Программа снабжена тремя механизмами вывода результатов работы: на экран в виде таблицы, в текстовый файл, а также в файл списка математического пакета WaterlooMaple. Это позволяет наглядно представить полученное решение.

Программа написана на языке программирования высокого уровня Borland C++ 3.1 в виде приложения MS-DOS. Обеспечивается полная совместимость программы со всеми широко известными операционными системами корпорации Майкрософт: MS-DOS 5.x, 6.xx, 7.xx, 8.xx, Windows 9x/Me/2000/NT/XP.

2.3 Пример работы программы

В качестве примера рассмотрим численное решение следующего дифференциального уравнения параболического типа:

,

Задав прямоугольную сетку с шагом оси 0.1 и по оси 0.01, получим следующее решение:

2.10 1.91 1.76 1.63 1.53 1.44 1.37 1.31 1.26 1.22 1.18

2.11 1.75 1.23 1.20 1.15 1.10 1.07 1.04 1.04 1.07 1.21

2.12 1.61 0.95 0.96 0.93 0.91 0.90 0.90 0.94 1.03 1.24

2.13 1.51 0.79 0.81 0.81 0.80 0.81 0.83 0.89 1.03 1.27

2.14 1.45 0.69 0.73 0.74 0.74 0.76 0.80 0.88 1.04 1.31

2.15 1.41 0.64 0.69 0.70 0.71 0.74 0.79 0.89 1.05 1.34

В таблице ось x расположена горизонтально, а ось t расположена вертикально и направлена вниз.

На выполнение программы на среднестатистическом персональном компьютере тратится время, равное нескольким миллисекундам, что говорит о высокой скорости алгоритма.

Подробно выходной файл output.txt, содержащий таблицу значений функции представлен в приложении 3.

В работе был рассмотрен метод сеток решения параболических уравнений в частных производных. Раскрыты основные понятия метода, аппроксимация уравнения и граничных условий, исследована разрешимость и сходимость получаемой системы разностных уравнений.

На основании изученного теоретического материала была разработана программная реализация метода сеток, проанализирована ее сходимость и быстродействие, проведен тестовый расчет, построен графики полученного численного решения.

1. Березин И.С., Жидков Н.П.Методы вычислений. Т.2. – М.: Физматгиз, 1962.

2. Тихонов А.Н., Самарский А.А.Уравнения математической физики. – М.: Наука, 1972.

3. Пирумов У.Г.Численные методы. – М.: Издательство МАИ, 1998.

4. Калиткин Н.Н.Численные методы. – М.: Наука, 1976.