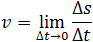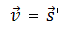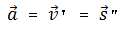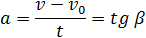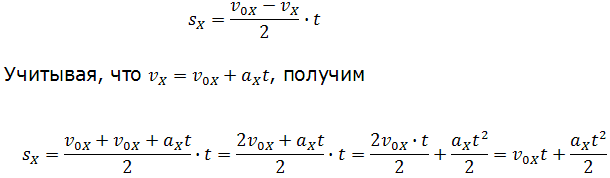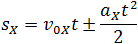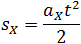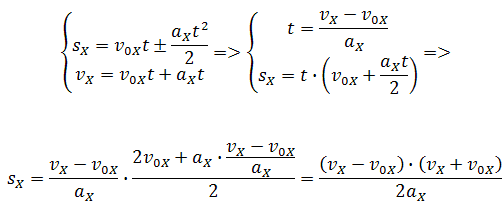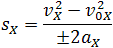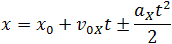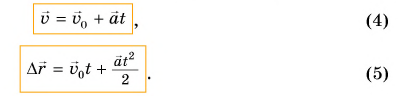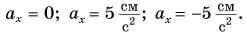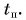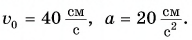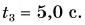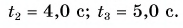Равнопеременное прямолинейное движение
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
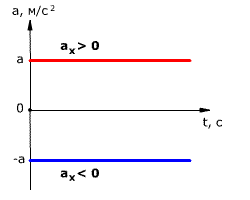
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
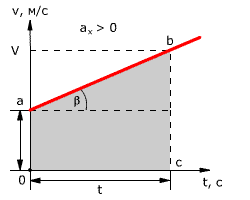
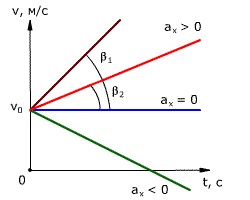
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
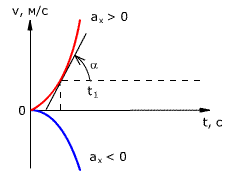
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx
Прямолинейное равнопеременное движение
Прямолинейное равнопеременное движение — движение тела вдоль прямой, характеризующееся постоянным по модулю и направлению линейным ускорением.
Траектория такого движения — прямая, поэтому в задачах равнозначными являются понятия пути и модуля перемещения. Такое движение может быть описано несколькими соотношениями:
- вектор скорости тела при равнопеременном движении
- где
- — вектор конечной скорости движения
- — вектор начальной скорости движения
- — вектор ускорения
- — время движения
- вектор перемещения тела при равнопеременном движении
Однако это векторные уравнения, с которыми работать достаточно сложно, а иногда, просто не хочется. Попробуем, анализируя условия задачи, составить уравнения скалярного вида, спроецировав вектора на некую ось.
Рис. 1. Равноускоренное движение 1
Пример 1. Тело движется прямо с начальной скоростью и ускоряется. По задаче выставляем вектора на ось OX (движение прямолинейное) (рис. 1). Сказано, что тело движется вдоль оси (вектор направлен по оси) и ускоряется (вектор также направлен вдоль оси). Осталось зафиксированные вектора спроецировать:
- Для уравнения (1):
- Для уравнения (2):
В общем случае, мы не можем предугадать направления векторов и , соответственно, мы не можем указать точный знак проекции этих векторов на выбранную ось. Но не заморачиваемся: в результате решения задачи мы получим одно и то же по модулю число, даже если ошибёмся. Т.е. выбираем направления как хотим, а потом анализируем ответ.
Рис. 2. Равноускоренное движение-2
Пример 2. Тело движется в положительном направлении оси и затормаживает. По задаче тело движется вдоль оси (вектор направлен по оси), а торможение говорит о том, что вектор ускорения ( ) направлен против оси OX (рис. 2). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Рис. 3. Равноускоренное движение-3
Пример 3. Тело движется в отрицательном направлении оси и затормаживает. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а торможение говорит о том, что вектор ускорения ( ) направлен против движения, а значит, по оси OX (рис. 3). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Рис. 4. Равноускоренное движение-4
Пример 4. Тело движется в отрицательном направлении оси и ускоряется. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а ускорение говорит о том, что вектор ускорения ( ) направлен в сторону движения, а значит, против оси OX (рис. 4). Проецируем:
- Для уравнения (1):
- Для уравнения (2):
Вывод: только что мы получили восемь различных формул, применимых для решения задач. Очень не хотелось бы их помнить. К счастью, есть выход: запомнить и понять векторный вид этих уравнений (1) и (2), а далее, применительно к данной вам задаче, просто адаптировать их, используя проекции.
Кроме формул (1) и (2), имеется ещё одна расчётная формула, которая чаще всего используется, когда в задаче на нужно найти время или его не дано. Воспользуемся уже имеющимися (1) и (2), считая движение тела равноускоренным. Выделим из (1) время:
Подставим (3) в (2) при условии :
Таким образом, мы получили формулу, в которой нет параметра времени.
Перемещение, координата и путь при равнопеременном движении в физике с примерами
Перемещение, координата и путь при равнопеременном движении:
Мы знаем, что при равнопеременном движении скорость тела линейно зависит от времени. А как зависит от времени перемещение? Координата? Пройденный путь?
В предыдущем параграфе для равнопеременного движения была найдена зависимость проекции скорости от времени:
и получена формула для проекции перемещения:
Подставляя 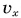
Отметим, что при движении с постоянным ускорением соотношения (1) и (3) выполняются и для векторов скорости и перемещения:
Учитывая, что проекция перемещения 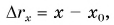
Формула (6) выражает кинематический закон равнопеременного движения. Функции (3) и (6) называются квадратичными. Следовательно, при равнопеременном движении проекция перемещения тела и его координата квадратично зависят от времени.
Сравним зависимости основных кинематических величин от времени для двух видов прямолинейного движения: равномерного и равнопеременного (табл. 1).
Таблица 1
Из таблицы видно, что при 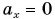
Рассмотрим графики проекций 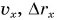
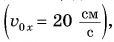
По формуле (1) 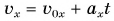
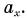
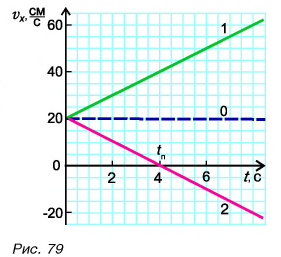
Перейдем к графикам проекции перемещения 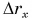
Как мы знаем, при 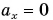
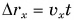
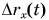
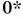
Из таблицы 1 видно, что формулы для проекции перемещения 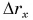
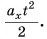
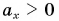
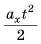
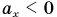
Так как 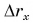
Обратите внимание на поведение графиков 2 и 2* в момент поворота 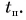
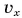
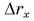
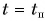
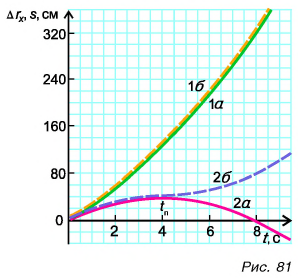
А каким будет график пути? Для движения, при котором направление скорости не изменяется, график пути 1б (рис. 81) совпадает с графиком проекции перемещения 1а. Если же скорость меняет свое направление, то график пути s (2б) и график проекции перемещения 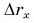
При 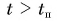
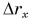
От графика проекции перемещения 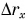
Так как, согласно формуле (6), 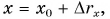
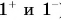
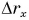
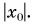
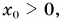
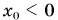
Выразим время из формулы проекции скорости (1): 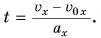
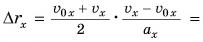
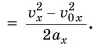
В случае когда начальная скорость и ускорение одинаково направлены, из равенства (7) следует:
где s — пройденный путь.
Главные выводы:
- При равнопеременном движении тела его перемещение и координата — квадратичные функции времени.
- Графики зависимости проекции перемещения и координаты от времени для равнопеременного движения являются участками парабол.
- Вершина параболы на графике проекции перемещения соответствует моменту времени, при котором мгновенная скорость равна нулю.
Пример решения задачи:
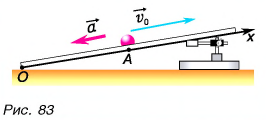
Шарику, находящемуся в точке А, расположенной посередине наклонного желоба длиной 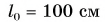
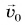
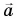
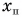
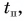
Определите время, когда шарик вернется в точку А, и время, когда он окажется в точке О. Постройте графики проекций скорости и перемещения, а также координаты шарика.
Пример решения задачи:
Решение
Выберем ось Ох, как показано на рисунке 83. Тогда проекция скорости 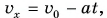
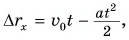
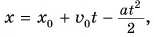
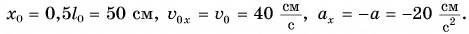
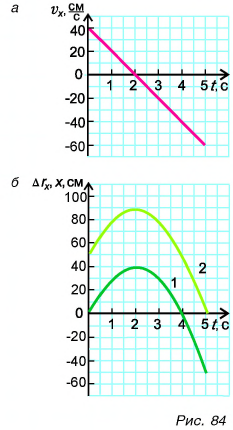
По этим формулам для моментов времени 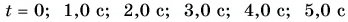
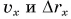
Используя полученные значения, строим графики проекций скорости (рис. 84, а) и перемещения (рис. 84, б, график 1) за промежуток времени от 0 до 5 с.
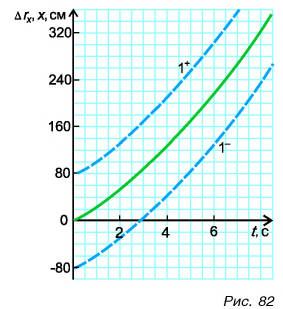
График координаты получим, сдвинув график проекции перемещения на 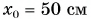
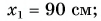
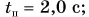
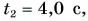
Ответ: 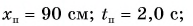
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Криволинейное движение
- Ускорение точки при ее движении по окружности
- Инерциальные системы отсчета
- Энергия в физике
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Ускорение в физике
- Скорость при равнопеременном движении
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://www.abitur.by/fizika/teoreticheskie-osnovy-fiziki/mexanicheskoe-dvizhenie/pryamolinejnoe-ravnoperemennoe-dvizhenie/
http://www.evkova.org/peremeschenie-koordinata-i-put-pri-ravnoperemennom-dvizhenii-v-fizike