Уравнения плоскости в пространстве прямая в пространстве

Уравнения прямой, виды уравнений прямой в пространстве

Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.

Уравнение прямой в пространстве: общие сведения

Уравнение прямой на плоскости в прямоугольной системе координат O x y – это линейное уравнение с переменными x и y , которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек.

Если речь идет о прямой в трехмерном пространстве, все несколько иначе: не существует такого линейного уравнения с тремя переменными x , y , z , которому бы отвечали только координаты точек заданной прямой. В самом деле, уравнение A x + B y + C z + D = 0 , где x , y , z – переменные, а А , В , С и D – некоторые действительные числа ( А , В , С одновременно не равны нулю) – это общее уравнение плоскости. Тогда как же задать прямую линию в прямоугольной системе координат O x y z ? Найдем ответ на этот вопрос в следующих пунктах темы.

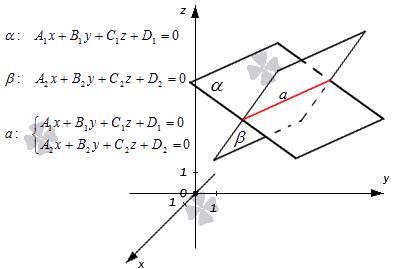
Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей

Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.

Рассмотрим это утверждение в алгебраическом толковании.

Допустим, в трехмерном пространстве зафиксирована прямоугольная система координат O x y z и задано, что прямая a – это линия пересечения двух плоскостей α и β , которые соответственно описываются уравнениями плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Поскольку прямая a – это множество общих точек плоскостей α и β , то координаты любой точки прямой a будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут.

Таким образом, координаты любой точки прямой a в прямоугольной системе координат станут частным решением системы линейных уравнений вида

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Общее же решение системы уравнений _ A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определит координаты каждой точки прямой a , т.е. по сути задает саму прямую a .

Резюмируем: прямая в пространстве в прямоугольной системе координат O x y z может быть задана системой уравнений двух плоскостей, которые пересекаются:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Приведем пример описания прямой линии в пространстве при помощи системы уравнений:

x + 3 y — 2 1 z + 11 3 y + 1 4 z — 2 = 0

Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.

Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.

Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.

Параметрические уравнения прямой в пространстве

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где x 1 , y 1 , z 1 – координаты некой точки прямой; а x , а y и a z (одновременно не равны нулю) – координаты направляющего вектора прямой. а · λ – некий параметр, принимающий любые действительные значения.

Любое значение параметра λ позволяет, используя параметрические уравнения прямой в пространстве, определить тройку чисел ( x , y , z ) , соответствующую некой точке прямой (отсюда и название такого вида уравнений). Например, пусть λ = 0 , тогда из параметрических уравнений прямой в пространстве получим координаты:

x = x 1 + a x · 0 y = y 1 + a y · 0 z = z 1 + a z · 0 ⇔ x = x 1 y = y 1 z = z 1

Рассмотрим конкретный пример:

Пусть прямая задана параметрическими уравнениями вида x = 3 + 2 · a x y = — 2 · a y z = 2 + 2 · a z .

Заданная прямая проходит через точку М 1 ( 3 , 0 , 2 ) ; направляющий вектор этой прямой имеет координаты 2 , — 2 , 2 .

Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.

Канонические уравнения прямой в пространстве

Если разрешить каждое из параметрических уравнений прямой

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ относительно параметра λ , возможно просто перейти к каноническим уравнениям прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z .

Канонические уравнения прямой в пространстве задают прямую, которая проходит через точку М 1 ( x 1 , y 1 , z 1 ) , и у которой направляющий вектор равен a → = ( a x , a y , a z ) . Например, задана прямая, описываемая каноническим уравнением x — 1 1 = y 2 = z + 5 7 . Эта прямая проходит через точку с координатами ( 1 , 0 , — 5 ) , ее направляющий вектор имеет координаты ( 1 , 2 , — 7 ) .

Отметим, что одно или два числа из чисел а x , а y и а z в канонических уравнениях прямой могут быть равны нулю (все три числа не могут быть равны нулю, поскольку направляющий вектор не может быть нулевым). В таком случае запись вида x — x 1 a x = y — y 1 a y = z — z 1 a z является формальной (поскольку в знаменателях одной или двух дробей будут нули) и понимать ее нужно как:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где λ ∈ R .

Если одно из чисел а x , а y и a z канонического уравнения прямой равно нулю, то прямая лежит в какой-то из координатных плоскостей, или в плоскости, ей параллельной. Если два из чисел а x , а y и a z равны нулю, то прямая или совпадает с какой-либо из координатных осей, или параллельна ей. К примеру, прямая, описываемая каноническим уравнением x + 4 3 = y — 5 2 = z + 2 0 , лежит в плоскости z = — 2 , параллельной координатной плоскости O x y , а координатная ось O y описывается каноническими уравнениями x 0 = y 1 = z 0 .

Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.

Уравнения плоскости в пространстве прямая в пространстве

Пусть в декартовой системе координат дан вектор n = и точка М 0 =( x 0 , y 0 , z 0 ).

Построим плоскость Π, проходящую через т. М 0 , перпендикулярную вектору n (этот вектор называют нормальным вектором или нормалью плоскости).

Утверждение 1: М Π ó М 0 М n .

М 0 М= < x-x 0 , y-y 0 , z-z 0 > n ó A( x-x 0 )+B( y-y 0 )+C( z-z 0 )=0. (*)

Каноническое уравнение плоскости в пространстве:

Аx+By+Cz+D=0, где D = -A x 0 -B y 0 -C z 0 .

Замечание 1: формула (*) используется при непосредственном решении задач, после упрощения получается искомое каноническое уравнение плоскости.

Пример 1. Написать каноническое уравнение плоскости, перпендикулярной вектору n= <3,1,1>и проходящей через точку М(2,-1,1).

Пример 2. Написать каноническое уравнение плоскости, содержащей точки K(2,1,-2), L(0,0,-1), M(1,8,1).

Пусть в декартовой системе координат дан вектор a =и точка М 0 =( x 0 , y 0 , z 0 ).

Построим прямую l , проходящую через т. М 0 , параллельную вектору a (этот вектор называют направляющим вектором прямой).

Утверждение 2: М l ó М 0 М || a .

М 0 М= < x-x 0 , y-y 0 , z-z 0 >|| a ó t R , т.ч. М 0 М=t ·a =>

Параметрические уравнения прямой в пространстве:

(**)

Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.

В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t 0 =0 он находится в точке М 0 , в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).

Теперь несколько преобразуем формулы (**).

Выразим из каждой строчки параметр t:

Канонические уравнения прямой в пространстве:

Замечание 2: Эта компактная запись на самом деле содержит три уравнения.

Замечание 3: Это формальная запись и выражение вида в данном случае допустимо.

Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.

Пример 3. Написать канонические и параметрические уравнения прямой, параллельной заданной прямой и проходящей через заданную точку.

Пример 4. Написать канонические уравнения прямой, заданной пересечением двух плоскостей.

Пример 5. Найти точку пересечения прямой и плоскости.

Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М 1 =(x 1 ,y 1 ,z 1 ).

Утверждение 3: расстояние от точки М 1 до плоскости Π вычисляется по формуле:

Пример 6. Найти расстояние от точки до плоскости.

Пусть в декартовой системе координат М 1 =(x 1 ,y 1 ,z 1 ), М 2 =(x 2 ,y 2 ,z 2 ) .

Утверждение 4: Координаты т. М, т.ч. М 1 М=λ∙ММ 2 , находятся по следующим формулам:

.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Прямая, плоскость и их уравнения

Начальные сведения

Введено понятие прямой, показаны принятые обозначения, рассмотрены варианты взаимного расположения прямой и точки, двух прямых, перечислены способы задания прямой на плоскости.

Получите представление о прямой линии в пространстве, рассмотрите варианты взаимного расположения прямых и способы задания прямой в пространстве.

Дано понятие плоскости в трехмерном пространстве, представлены варианты ее взаимного расположения с точкой, прямой и другой плоскостью, показаны способы задания.

Уравнения прямой на плоскости

Что называют уравнением прямой и какие виды уравнения прямой на плоскости существуют? В этой статье Вы найдете ответы на эти вопросы.

Познакомьтесь с направляющим вектором прямой, узнайте как его координаты участвуют в записи уравнения прямой.

Узнайте что такое нормальный вектор прямой и как определяются его координаты по уравнению прямой на плоскости.

Всесторонне разобрано общее уравнение прямой, показаны неполные уравнения, приведены примеры и графические иллюстрации.

Научитесь работать с каноническими уравнениями прямой, разберитесь как в их записи участвуют координаты направляющего вектора прямой, рассмотрите решения характерных задач.

Откройте для себя уравнение прямой в отрезках, узнайте почему оно получило такое название и почему с помощью уравнения этого вида легко построить прямую с прямоугольной системе координат.

Рассмотрено уравнение прямой с угловым коэффициентом, введены определения угла наклона и углового коэффициента, разобраны решения характерных задач на составление уравнений прямой этого вида.

Познакомьтесь с параметрическими уравнениями прямой на плоскости, научитесь от уравнений прямой другого вида переходить к параметрическим уравнениями и обратно.

Узнайте как выводится нормальное уравнение прямой и как оно применяется для нахождения расстояния от точки до прямой.

Уравнения плоскости

Узнайте какими уравнениями описываются плоскости в прямоугольной системе координат в трехмерном пространстве.

Запомните определение нормального вектора плоскости, посмотрите как его координаты участвуют в записи уравнений плоскости.

Познакомьтесь с полными и неполными общими уравнениями плоскости, рассмотрите примеры и решения характерных задач.

Показано как из общего уравнения плоскости получить уравнение плоскости в отрезках и как его использовать для построения плоскости.

Разобрано как нормальное (нормированное) уравнение плоскости получается из общего и как оно применяется для нахождения расстояния от точки до плоскости.

Уравнения прямой в пространстве

Показано с помощью каких уравнений можно задать прямую линию в пространстве в заданной прямоугольной системе координат.

Разобрано как прямая линия в прямоугольной системе координат в пространстве задается уравнениями двух пересекающихся плоскостей.

Познакомьтесь с параметрическими уравнениями прямой в пространстве, рассмотрите примеры их составления и способы перехода к уравнениям другого вида.

Подробно рассмотрены канонические уравнения прямой в пространстве, показана их связь с другими видами уравнений, приведены решения характерных примеров и задач.

Параллельность и перпендикулярность

Даны основные сведения о параллельных прямых, перечислены признаки и условия параллельности прямых в том числе через направляющие и нормальные векторы.

Приведены начальные сведения о перпендикулярных прямых, разобраны признаки и условия перпендикулярности прямых.

Получите основные сведения о параллельных прямой и плоскости, научитесь выяснять параллельны ли прямая и плоскость.

Примите к сведению условия и признаки перпендикулярности прямой и плоскости, ознакомьтесь с решением характерных примеров.

Познакомьтесь с определением параллельных плоскостей и с условиями параллельности, разберите решения характерных примеров и задач.

Приведены признаки и условия перпендикулярности плоскостей, позволяющие устанавливать параллельны ли плоскости, заданные своими уравнениями.

Составление уравнений прямой

Научитесь составлять уравнение прямой, когда известны координаты двух лежащих на ней точек, в этом Вам помогут прведенные решения примеров с пояснениями.

Узнайте как составляются уравнения прямой, когда известны уравнения параллельной ей прямой и координаты точки, через которую она проходит.

Разберитесь с составлением уравнений прямой, проходящей через данную точку перпендикулярно заданной прямой, рассмотрите решения характерных примеров.

Познакомьтесь с принципом составления уравнений прямой, которая проходит через заданную точку перпендикулярно заданной плоскости.

Показана суть составления уравнений прямой для данных условий, приведены готовые решения примеров.

Составление уравнений плоскости

Узнайте как составляется уравнение плоскости, когда даны координаты трех ее точек, рассмотрите решения примеров.

На примерах показано как составить уравнение плоскости, когда известно уравнение лежащей на ней прямой и координаты точки.

Научитесь записывать уравнение плоскости, которая проходит через две заданные параллельные или пересекающиеся прямые.

Показано как составляется уравнение плоскости, если известны координаты одной ее точки и уравнение прямой, которой она перпендикулярна.

Разберитесь с составлением уравнения плоскости, когда известны координаты точки, через которую она проходит, и уравнение плоскости, которой она параллельна.

Показаны примеры составления уравнения плоскости, которая перпендикулярна двум заданным плоскостям и проходит через заданную точку.

Нахождение углов методом координат

Получена формула для нахождения косинуса угла и самого угла между пересекающимися прямыми, показаны решения примеров.

Дано определение угла между скрещивающимися прямыми и разобрано как находить этот угол методом координат.

Узнайте как находить угол между прямой и плоскостью когда известны их уравнения, разберитесь в решениях характерных примеров.

Разберитесь с нахождением угла между пересекающимися плоскостями, запомните формулу и рассмотрите приведенные решения примеров.

Нахождение координат точек пересечения

Узнайте как находить координаты точки пересечения двух прямых на плоскости и в пространстве, разберите решения характерных задач.

На примерах показаны способы нахождения координат точки пересечения прямой и плоскости.

Нахождение расстояний методом координат

Разобраны различные способы нахождения расстояния от заданной точки до заданной прямой, в том числе с использованием нормального уравнения прямой, приведены решения примеров.

Научитесь находить расстояние от точки до плоскости методом координат, для этого удобно использовать нормальное уравнение плоскости.

Познакомьтесь со способами нахождения расстояния между параллельными прямыми в прямоугольной системе координат.

Узнайте как определяется расстояние между скрещивающимися прямыми, разберите примеры нахождения расстояния методом координат.

Показано как находить расстояние между прямой и плоскостью, которые параллельны, для пояснения приведены решения примеров.

Разберитесь с нахождением расстояния между параллельными плоскостями, когда известны их уравнения.

Связки и пучки

Узнайте что такое пучок прямых, рассмотрите его уравнение и связанные с пучками прямых характерные примеры.

Познакомьтесь с пучком плоскостей и видом уравнения пучка плоскостей.

Дано определение связки плоскостей и ее уравнение, показаны решения примеров.

Проекция точки на прямую и плоскость

Узнайте что называют проекцией точки на прямую и как находятся координаты проекции.

Показано как находить координаты проекции точки на плоскость, разобраны решения примеров.