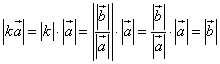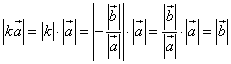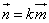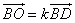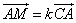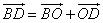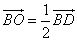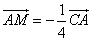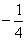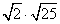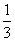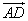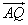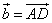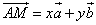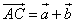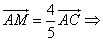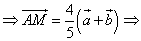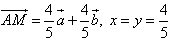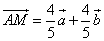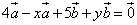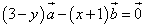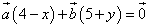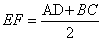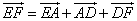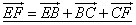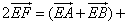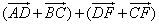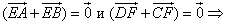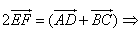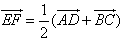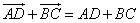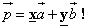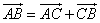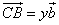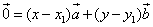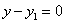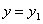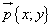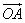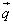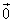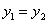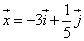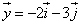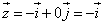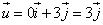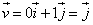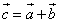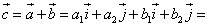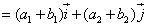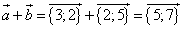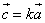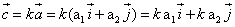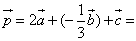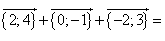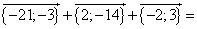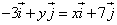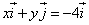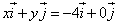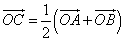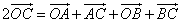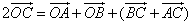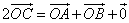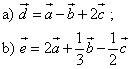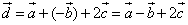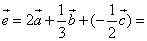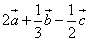Векторы
Корзина

На данной онлайн странице электронного справочника по математике для школьников представлены следующие готовые домашние задания, решения тестовых заданий по геометрии 9 класса:
- – представлены определения вектора, скалярных и векторных величин;
- – в примерах с номерами 9 — 12 рассматривается, как решать геометрию по теме «Коллинеарные векторы»;
- – решения векторов представлены в теме «Разложение вектора по двум неколлинеарным векторам». Контрольные работы 13 — 15;
- – тема «Координаты вектора» объясняется в работах 16 — 22 учебника. В данной рабочей тетради показываются ответы к вопросам, как решать задачи, если требуется найти координаты суммы, разности векторов и произведения вектора на число;
- – задачи 1 — 8 показывают примеры решений и ответы по математике, изученных на материале курса геометрии 8 класса. Здесь рассматриваются тесты и задания по таким разделам, как средняя линия треугольника, параллелограмм, площадь треугольника, равнобедренная трапеция, вписанные и описанные окружности.
Понятие вектора
Автобус едет из города Анск в город Бинск. На карте город Анск обозначим латинской буквой A, город Бинск – буквой B латинского алфавита.

Соединив точки A и B, получаем отрезок AB. При этом точка A – начало отрезка или пункт отправления автобуса, т.е. откуда едет автобус, точка B – конец отрезка или пункт назначения автобуса, куда движется автобус.
Отрезок AB изображает схему маршрута автобуса.
Направление движения автобуса, или направление маршрута, или направление отрезка AB обозначим стрелкой –>.

Выражение «A –> B» обозначает схематичное движение автобуса из пункта A в пункт B.
Отрезок со стрелкой – направленный отрезок.
Определение:
Вектор – направленный отрезок.
В математике принято обозначать вектор как 
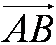

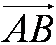
Часто вектор могут обозначать маленькой буквой 
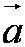
Когда A – начальная точка отрезка и B – конечная точка отрезка совпадают, то есть когда отрезок отсутствует, тогда вектор считается нулевым и обозначается как 
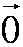
Длина отрезка AB, расстояние между городом Анск и Бинск, – абсолютная величина вектора , или модуль вектора 
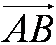

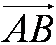
Модуль вектора обозначается как 
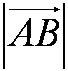
Например, дано 
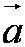

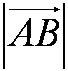
Длина нулевого вектора обозначается как 
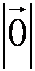

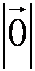
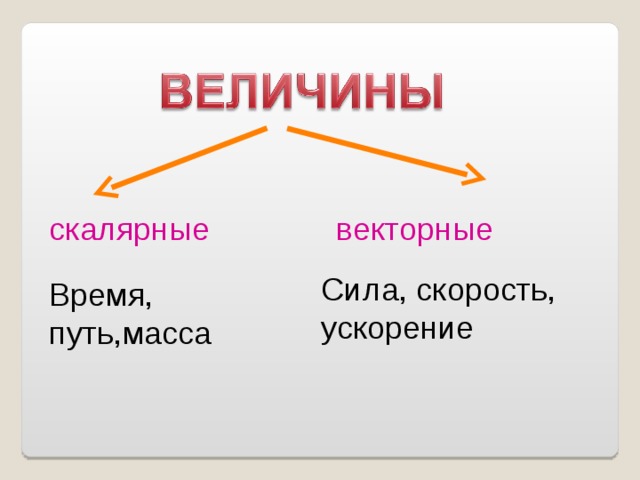
Скалярные и векторные величины
Величина может быть скалярной или векторной.
Величина является скалярной, если содержит численное значение, но не указывает на направление. Например, 5 книг, 10 метров ткани, где цифры «5», «10» – скалярные величины.
Векторная величина или вектор – величина, которая содержит количественное значение и указывает на направление.
Например, автобус едет или совершает перемещение из пункт A в пункт B со скоростью 30 км/ч.
Цифра «30» – скорость автобуса в км/ч – пример векторной величины, так как дано численное значение и указывается направление движения.
Перемещение точки, которая движется в данный момент времени, – вектор с начальной точкой в точке старта движения и с конечной точкой в точке, где данная точка находится в это время.


Например, AB = 5 км, BC = 5 км, CD = 3 км, DE = 2 км, AE = 4 км.
Длина маршрута движения автобуса из пункта A в пункт E составляет
L = AB + BC + CD + DE = 15 км.
Длина маршрута – скалярная величина, так как дано только количество километров – «15» без указания на направление движения.
Перемещение – вектор 
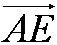
AE = 4 км. Перемещение – векторная величина, где число «4» – количество километров, АЕ – указывает на направление движения, из пункта Анск в пункт Eнск.
Допустим, автобус проехал 30 км: в одну сторону, из Анска в Енск – 15 км, а также обратно, из Енска в Анск – 15 км. В этом примере перемещение равно 0 км и является нулевым вектором.
Коллинеарные векторы
Лемма – теорема, вспомогательная для доказательства следующей теоремы.
Лемма о коллинеарных векторах:
Если векторы 


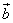

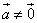

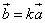

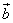


Дано: вектор a, вектор b
Векторы 


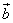

Доказать: есть такое число k, что верно равенство 







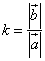




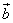

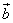

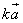

Значит, 

2 случай.
Пусть a, b — противоположные векторы, т.е. 


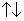

Возьмем 
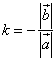

Следовательно, 
Задача 9.
вектор m, вектор n

1) 
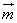

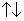

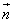



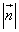
2) 
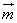

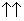

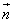



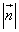
Решение: 1) Т.к. 
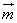

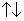

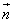
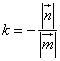

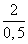
Решение: 2) Т.к. 
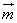

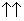

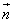

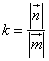

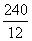
Задача 10.


BD 
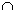
M – середина отрезка AO
1) 
2) 
1) Т.к. 
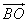

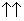

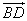

По свойству параллелограмма

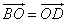

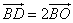



Ответ: k= 
2) Т.к. 
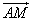

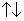

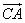
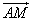

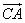
Т.к. k
Ответ: k= 
Задача 11.
Дано: 
1) 
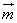

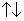

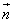



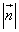
2) 
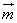

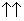

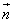



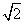

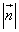

Решение: 1) Т.к. 
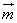

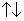

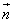
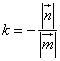

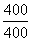
Решение: 2) Т.к. 
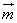

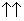

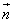

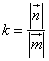

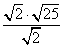

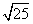
Задача 12.
Решить уравнение: найти значения x, y.

Решить уравнение: найти значения x, y.

y = 
Ответ: x= – 1, y= 
Разложение вектора по двум неколлинеарным векторам
Определение: Если 
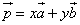



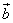

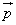



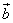



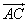

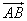


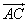

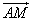


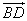

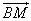


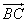

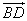

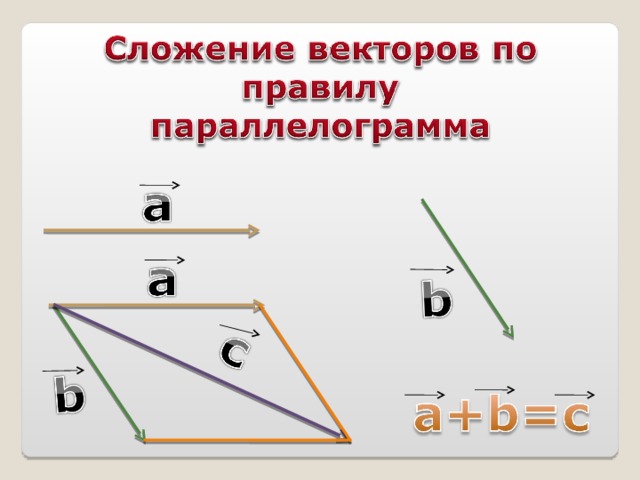
а) По правилу параллелограмма 
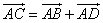
б) 
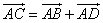

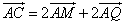
в) 
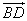

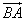

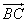

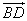

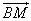

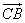
г) Т.к. 
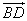

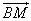

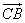



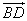

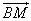


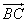

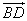

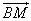

Задача 13.
Дано: ABCD – параллелограмм

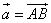

M 
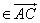
Найти: 
По правилу параллелограмма

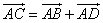

Но 
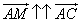



Ответ: 
Задача 14.
Дано: векторы 


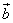
а) 
б) 
Найти: коэффициенты разложения x, y – ?
а) 
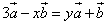



3 – y = 0, x+1=0 

б) 
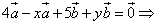

4 – x = 0, 5+y=0 

Ответ: a) x= –1, y= 3 б) x = 4, y= –5


Задача 15.
Дано: ABCD – трапеция
EF – средняя линия трапеции
Доказать: EF 
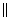

— т.е. длина средней линии трапеции равна полусумме основанию трапеции.
По правилу многоугольника


Сложив оба выражения, получаем


Т.к. E и F – середины сторон AB и CD, тогда



Т.к. 
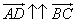

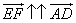

Поэтому EF || AD и 


Теорема: Любой вектор 
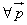
вектор a, вектор b



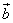
Доказать: 
Через точку А и точку В проведем прямые, параллельные прямым, содержащих векторы 


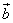
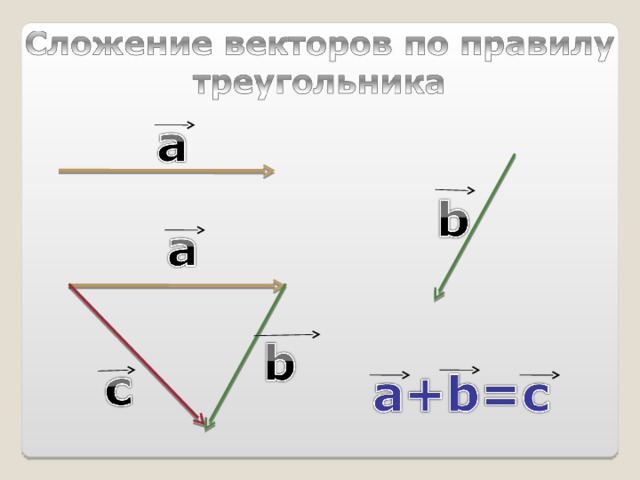
Тогда по правилу треугольника

Заметим, что векторы 


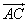

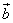

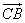
По лемме о коллинеарных векторах

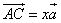

Тогда 
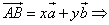

Единственность разложения
Знаем, что 
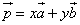
Пусть есть 
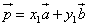
В результате разности выражений (1) и (2) получаем

Это равенство возможно

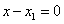

Т.е 
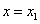

Координаты вектора
Определение: Единичным вектором называется вектор, длина которого равна единице.
i и j – координатные векторы
Т.к. 
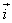

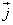

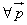

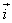

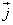
Т.е. 
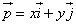


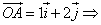


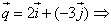


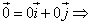

Если 
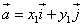

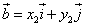
то 
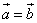

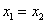

Задача 16.
Найти координаты векторов.

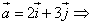


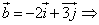


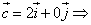





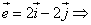


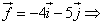

Задача 17.
Найти координаты векторов.

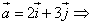


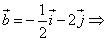

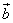



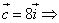


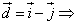


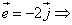


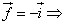

Задача 18.
Найти сумму вектора по его координатам.

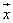

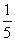




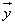




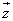




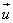




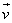



Правила, позволяющие по координатам векторов находить координаты суммы, разности векторов и произведения вектора на число.
1. Суммой векторов 


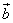

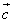



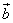

Доказать: 
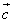
— сумма координат вектора, т.е. формула, как найти координаты вектора через сложение



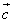
Пример 1 — сложение векторов, как найти координаты векторов:
Если даны координаты векторов 


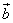

2. Разностью векторов 


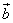

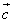
3. Произведением вектора 


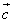

k – произвольное число

Доказать: 
— умножение вектора на число

Значит, вектор 
Пример 2 — как находить координаты вектора:
Найти координаты вектора 
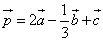



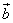



Ответ: 
Задача 19.
Найти координаты вектора 
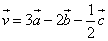



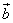


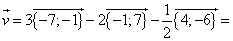

Ответ: 
Задача 20.
1) 
2) 
Найти: коэффициенты разложения x, y – ?
1) 
По теореме о разложении вектора по двум неколлинеарным векторам:
2) 

По теореме о разложении вектора по двум неколлинеарным векторам:
Задача 21.
Дано: координаты векторов
1) 


2) 


Найти: разность векторов 


1) 


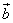

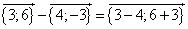



2) 


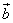

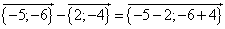



Задача 22.
Дано: координаты векторов

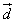

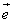

Найти: координаты векторов, противоположных данным.

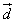




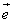




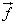



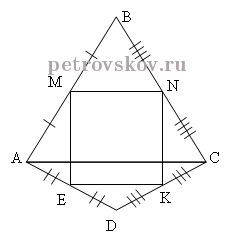
Задача 1.
M, N, K, E – середины сторон AB, BC, DC, AD 
Четырехугольник MNKE – параллелограмм
Соединим точку А и точку С.
Получим треугольник Δ ABC, где MN – средняя линия треугольника Δ ABC и треугольник Δ ADC, где EK – средняя линия треугольника Δ ADC.
По свойству средней линии треугольника Δ следует, что
MN || AC – параллельны и MN= 

EK || AC – параллельны и EK= 

Тогда MN || EK – параллельны и MN=EK, поэтому 
MNKE – параллелограмм (по первому признаку параллелограмма).


Задача 2.
Треугольник Δ ABC
Сторона треугольника AB = 8,5 см
Сторона треугольника AC = 5 см
Высота AH = 4 см, т.е отрезок AH перпендикулярен стороне BC
H 
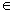
S ΔABC = 

По теореме Пифагора
BH = 
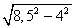

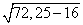

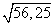
По теореме Пифагора
CH = 
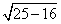

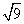
BC = BH + CH = 3 +7,5 = 10,5 см
S ΔABC = 


Ответ: S ΔABC = 21 
Задача 3.


ABCD – равнобедренная трапеция
Доказать: NE 
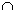

Проведем перпендикуляры BH и CH1, то есть BH 
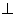

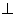
Но BH и CH1 проходят через NE 


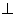

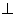
Стороны BH = CH1 равны 

Поэтому BH = KM = CH1 равны 


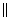

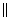
Следовательно углы равны 



Тогда 



Задача 4.
O – произвольная точка
Вектор OC равен половине суммы двух других векторов OA и OB, исходящих из одной и той же точки O




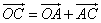

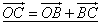
Сложив выражения (1) и (2), получаем




Задача 5.
Три вектора 
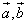

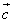


Суммы и разности векторов.

По правилу многоугольника
a) 

б) 
= 


Задача 6.
Доказать, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.
четырехугольник ABCD – равнобедренная трапеция
Доказать: EF 
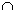

Проведем параллельные прямые
Получим равнобедренный треугольник ΔMKR
AB=MK, так как трапеция равнобедренная,
CD=MR, т.к. трапеция равнобедренная.
Следовательно, EF – средняя линия треугольника ΔMKR, поэтому
BM=MC=AK=RD, т.к. ABMK и MCDR – параллелограммы.
Тогда MN – медиана, биссектриса и высота равнобедренного треугольника ΔMKR.
Т.к. MN – высота, то отрезки MN 
По свойству средней линии треугольника Δ следует, что
Тогда EF 


Задача 7.
Доказать, что центр окружности, вписанной в равнобедренный треугольник, лежит на медиане, проведенной к основанию.
вписанная окружность в равнобедренном треугольнике
ΔABC – равнобедренный треугольник
Доказать: O 
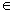
Проведем перпендикуляры OH1 ; OH2 ; OH3 к сторонам BC, AC, AB.
Здесь из двух точек проведен один и тот же перпендикуляр к стороне AC, но в треугольнике можно провести только один перпендикуляр к стороне и только из одной точки.
Следовательно, что O 
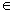
Задача 8.
Доказать, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию или на ее продолжение.


Описанная окружность около равнобедренного треугольника
Δ ABC – вписанный равнобедренный треугольник
Доказать: O 
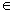
Проведем из центра окружности перпендикуляры
Здесь проведен из двух точек перпендикуляр к стороне AC, но в треугольнике можно провести только один перпендикуляр к стороне и только из одной точки.
Следовательно, что O 
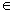
Примеры решения задач с векторами
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме — координаты вектора.
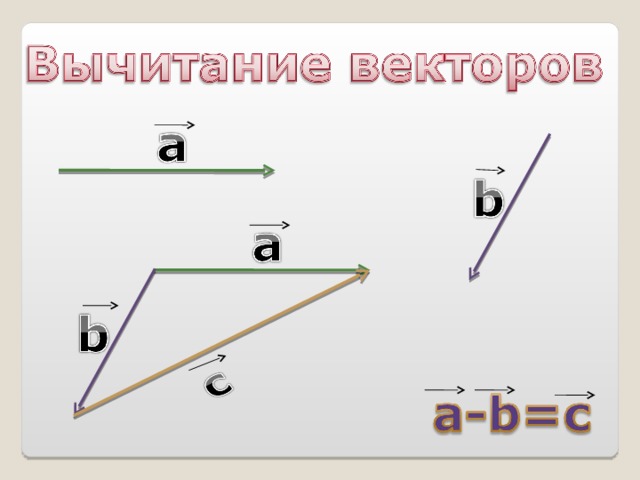
Векторы ( геометрия 9 класс)
В данной презентации систематизирован и обобщен материал по данной теме, известный учащимся. Рассмотрены правила действий с векторами, разобран ряд задач. Презентацию можно использовать на нескольких уроках, так как она содержит большой объем материала
Просмотр содержимого документа
«Векторы ( геометрия 9 класс)»
Муниципальное бюджетное общеобразовательное учреждение
«средняя общеобразовательная школа №4»
Презентации к урокам математики
Заслуженный учитель РФ
Кулиашвили Елена Николаевна


- Термин вектор (от лат. Vector – “ несущий “) впервые появился в 1845 г. у ирландского математика Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем.
Что такое вектор ?
Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением: например, скорость, сила, давление. Такие величины называются векторными величинами или векторами .
Сила, скорость, ускорение
ВЕКТОР или направленный отрезок – отрезок, у которого указано, какая из его граничных точек считается началом, а какая — концом
- векторы обозначают двумя заглавными латинскими буквами со стрелкой над ними или одной строчной латинской буквой со стрелкой над ней
- любая точка плоскости является нулевым вектором
- длиной или модулем ненулевого вектора АВ называется длина отрезка АВ
- Расстояние между началом и концом вектора называется длиной или модулем вектора. Длина вектора обозначается |а| или |АВ|.
- Длина нулевого вектора считается равной нулю.
(каждая клетка на рисунке имеет сторону, равную единице измерения отрезков)
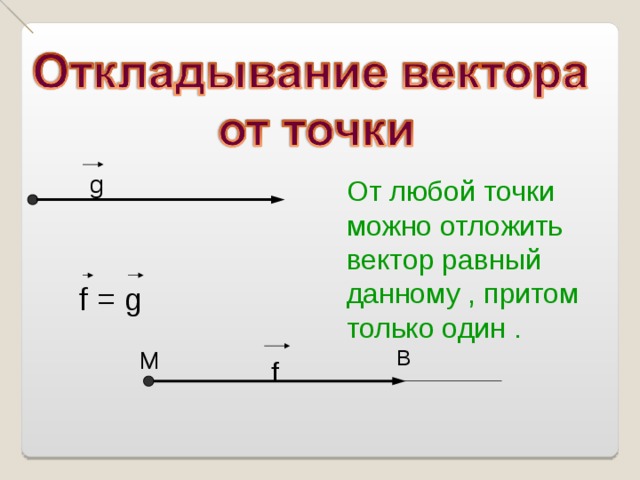
От любой точки можно отложить вектор равный данному , притом только один .
- ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых
- коллинеарные векторы могут быть направлены одинаково и называются сонаправленными или противоположно направлены и называются противоположно направленными
- Ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых.
- Нулевой вектор считается коллинеарным любому вектору.
CD, KF, O, a, b – коллинеарные
O, a – коллинеарные
O, NP – коллинеарные
NP, m – не коллинеарные
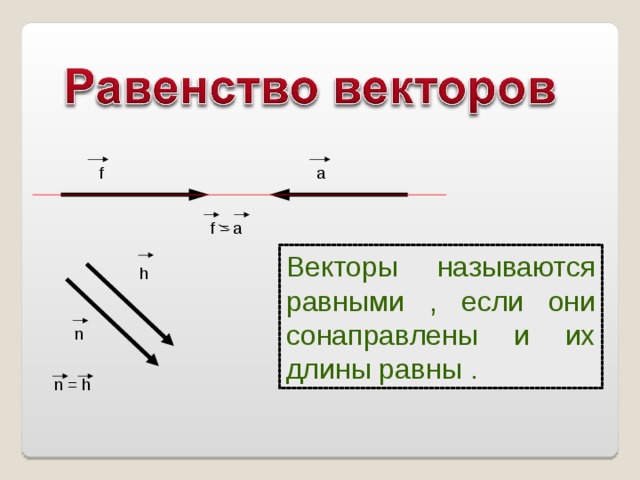
Векторы называются равными , если они сонаправлены и их длины равны .
Отложите эти векторы от одной точки.
- На рисунке изображена равнобедренная трапеция KLMN.
а) Укажите сонаправленные, противоположно направленные, равные вектора.
б) Укажите векторы, длины которых равны. Равны ли при этом сами векторы?

- Даны вектор BC и точка D(1;-2). Отложите от точки D вектор, равный вектору BC.
- Как должен быть расположен ненулевой векторaотносительно прямойk, чтобы нашлись лежащие на этой прямой векторы, равныеa? Сколько таких векторов найдется? Отметьте на чертеже три из них.
- Векторы AB и DC равны. Докажите, что если точки A, B, C и D не лежат на одной прямой, то четырехугольник ABCD―параллелограмм.
- На рисунке изображен параллелограмм ABCD.Укажите векторы, длины которых равны. Равны ли при этом сами векторы?
- В ромбе ABCD l AC l = 12см, l BD l = 16см. От вершины A отложен вектор AE, равный вектору BD. Найдите длину вектора EC.

Для любых чисел k , l и любых векторов a , b справедливы равенства :
Для любых чисел k , l и любых векторов a , b справедливы равенства :
- (kl )a = k (la ) ( сочетательный закон )
- (k+l) a = ka + la ( первый распределительный закон )
- K ( a+b ) = ka + kb (второй распределительный закон ) .
- (kl )a = k (la ) ( сочетательный закон )
- (k+l) a = ka + la ( первый распределительный закон )
- K ( a+b ) = ka + kb (второй распределительный закон ) .
http://www.webmath.ru/poleznoe/formules_4_14.php
http://multiurok.ru/files/vektory-geometriia-9-klass.html