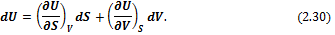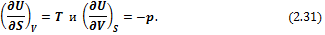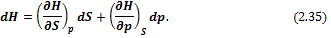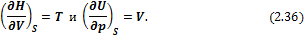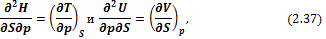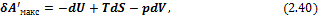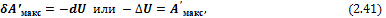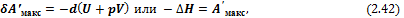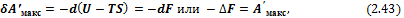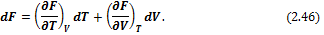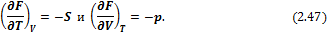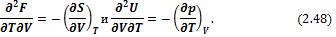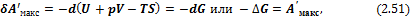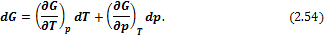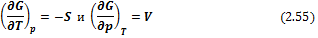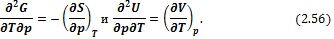Уравнения потенциалов из уравнений максвелла

Решение уравнений Максвелла; потенциалы и волновое уравнение

Теперь стоило бы заняться немного математикой; мы запишем уравнения Максвелла в более простой форме. Вы, пожалуй, сочтете, что мы усложняем их, но если вы наберетесь терпения, то внезапно обнаружите их большую простоту. Хотя вы уже вполне привыкли к каждому из уравнений Максвелла, имеется все же много частей, которые стоит соединить воедино. Вот как раз этим мы и займемся.

Начнем с V·В=0 — простейшего из уравнений. Мы знаем, что оно подразумевает, что В — есть ротор чего-то. Поэтому, если вы записали

то считайте, что уже решили одно из уравнений Максвелла. (Между прочим, заметьте, что оно остается верно для другого вектора А′, если A′=A+ vψ), где ψ — любое скалярное поле, потому что ротор vψ — нуль и В — по-прежнему то же самое. Мы говорили об этом раньше.)

Теперь разберем закон Фарадея VxE= –∂B/∂t, потому что он не содержит никаких токов или зарядов. Если мы запишем В как V X А и продифференцируем по t, то сможем переписать закон Фарадея в форме

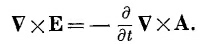Поскольку мы можем дифференцировать сначала либо по времени, либо по координатам, то можно написать это уравнение также в виде

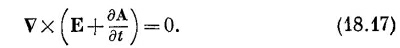Мы видим, что E+∂A/∂t — это вектор, ротор которого ранен нулю. Поэтому такой вектор есть градиент чего-то. Когда мы занимались электростатикой, у нас было VxE=0, и мы тогда решили, что Е — само градиент чего-то. Пусть это градиент от –φ (минус для технических удобств). То же самое сделаем и для E+∂A/∂t; мы полагаем

Мы используем то же обозначение φ, так что в электростатическом случае, когда ничто не меняется со временем и ∂A/∂t исчезает, Е будет нашим старым –vφ. Итак, закон Фарадея можно представить в форме

Мы уже решили два из уравнений Максвелла и нашли, что для описания электромагнитных полей Е и В нужны четыре потенциальные функции: скалярный потенциал φ и векторный потенциал А, который, разумеется, представляет три функции.

Итак, А определяет часть Е, так же как и В. Что же произойдет, когда мы заменим А на A′=A+vψ? В общем, Е должно было бы измениться, если не принять особых мер. Мы можем, однако, допустить, что А изменяется так, чтобы не влиять на поля Е и В (т. е. не меняя физики), если будем всегда изменять А и φ вместе по правилам

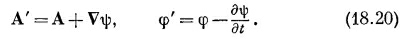Тогда ни В, ни Е, полученные из уравнения (18.19), не меняются.

Раньше мы выбирали V ·А=0, чтобы как-то упростить уравнения статики. Теперь мы не собираемся так поступать; мы хотим сделать другой выбор. Но подождите немного, прежде чем мы скажем, какой это выбор, потому что позднее станет ясно, почему вообще делается выбор.

Сейчас мы вернемся к двум оставшимся уравнениям Максвелла, которые свяжут потенциалы и источники ρ и j. Раз мы можем определить А и φ из токов и зарядов, то можно всегда получить Е и В из уравнений (18.16) и (18.19) и мы будем иметь другую форму уравнений Максвелла.

Начнем с подстановки уравнения (18.19) в v·E=ρ/ε₀; получаем

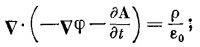это можно записать еще в виде

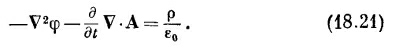Таково первое уравнение, связывающее φ и А с источниками.

Наше последнее уравнение будет самым трудным. Мы начнем с того, что перепишем четвертое уравнение Максвелла:

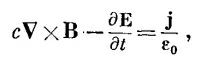а затем выразим В и Е через потенциалы, используя уравнения (18.16) и (18.19):

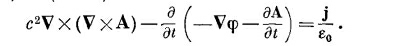Первый член можно переписать, используя алгебраическое тождество v x (vxA) = V (V·A) – v 2 A; мы получаем

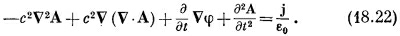Не очень-то оно простое!

К счастью, теперь мы можем использовать нашу свободу в произвольном выборе дивергенции А. Сейчас мы собираемся сделать такой выбор, чтобы уравнения для А и для φ разделились, но имели одну и ту же форму. Мы можем сделать это, выбирая ,

Когда мы поступаем так, то второе и третье слагаемые в уравнении (18.22) погашаются, и оно становится много проще:

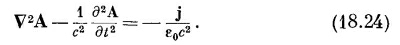И наше уравнение (18.21) для φ принимает такую же форму:

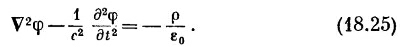Какие красивые уравнения! Они великолепны прежде всего потому, что хорошо разделились — с плотностью заряда стоит φ, а с током стоит А. Далее, хотя левая сторона выглядит немного нелепо — лапласиан вместе с (∂/∂t) 2 , когда мы раскроем ее, то обнаружим

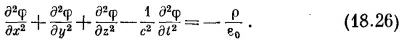Это уравнение имеет приятную симметрию по х, у, z, t; здесь (–1/с 2 ) нужно, конечно, потому, что время и координаты различаются; у них разные единицы.

Уравнения Максвелла привели нас к нового типа уравнению для потенциалов φ и А, но с одной и той же математической формой для всех четырех функций φ, А_х, А_у и A_z. Раз мы научились решать эти уравнения, то можем получить В и Е из vXE и —vφ —∂A/∂t. Мы приходим к другой форме электромагнитных законов, в точности эквивалентной уравнениям Максвелла; с ними во многих случаях обращаться гораздо проще.
Фактически мы уже решали уравнение, весьма похожее на (18.26). Когда мы изучали звук в гл. 47 (вып. 4), мы имели уравнение в форме

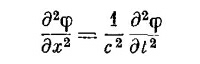и видели, что оно описывает распространение волн в x-направлении со скоростью с. Уравнение (18.26) это соответствующее волновое уравнение для трех измерений. Поэтому в области, где больше нет зарядов и токов, решение этих уравнений не означает, что φ и А — нули. (Хотя на самом деле нулевое решение есть одно из возможных решений.) Имеются решения, представляющие некоторую совокупность φ и А, которые меняются со временем, но всегда движутся со скоростью с. Поля передвигаются вперед через свободное пространство, как в нашем примере в начале главы.

С новым членом, добавленным Максвеллом в уравнение IV, мы смогли записать полевые уравнения в терминах А и φ в форме, которая проста и сразу же позволяет выявить существование электромагнитных волн. Для многих практических целей еще будет удобно использовать первоначальные уравнения в терминах E и В. Но они — по ту сторону горы, на которую мы уже вскарабкались. Теперь мы можем посмотреть вокруг. Все будет выглядеть иначе — нас ожидают новые, прекрасные пейзажи.

Характеристические функции. Вывод уравнений Максвелла. Термодинамические потенциалы

Подставим выражение (2.5) в уравнение (1.1); если речь идет о равновесном процессе, то при отсутствии любого вида работы, кроме работы расширения, можем записать:

Поскольку U – функция состояния, т. е. dU_равн. = dU_{неравн.}, то уравнение (2.22) применимо безотносительно к тому, равновесно или не равновесно осуществляется процесс. Уравнение (2.28) является обобщенной формой записи первого и второго законов термодинамики. Если (2.28) разрешить относительно энтропии, то получим соотношение

Уравнения (2.28) и (2.29) называют фундаментальными уравнениями Гиббса, они являются характеристическими, т.е. в них в явном виде представлена вся термодинамическая информация о системе; аналогично, функции S(U, V) и U(S, V) называют характеристическими функциями, а соответствующие им наборы переменных – естественными. Характеристической функцией называется функция состояния, посредством которой (и частных производных разных порядков ее по соответствующим ей переменным) могут быть наиболее просто и притом в явном виде выражены все термодинамические свойства системы.

Уравнение (2.28) показывает, что U является функцией энтропии и объема системы, т. е. U = f(S, V). Тогда

Сравнивая (2.30) и (2.28), можно констатировать, что

Таким образом, внутренняя энергия является характеристической функцией и ее частные производные выражают параметры системы. Исходя из (2.31), можно записать:

откуда следует, что

Уравнение (2.33) называется первым уравнением Максвелла.

Поскольку H = U + pV, тогда dH = dU + pdV, подставим это выражение в (2.28)

Таким образом, энтальпия является характеристической функцией энтропии и давления: H = f(S, p). Тогда

Сравнивая (2.35) и (2.34), получим

Исходя из (2.36), можно записать:

откуда следует, что

Соотношение (2.38) называется вторым уравнением Максвелла.

В общем случае уравнение (2.28), объединяющее первое и второе начала термодинамики, можно записать в виде

где 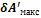–максимальная полезная работа (работа против электрических, магнитных и прочих сил); pdV – работа, затраченная на расширение (сжатие) и необходимая для поддержания в данное мгновение в системе давление р.

Из (2.40) вытекает наличие характеристических функций состояния системы, убыль которых в обратимом процессе, протекающем при постоянстве определенной пары термодинамических параметров, равна максимальной полезной работе. По аналогии с механикой, где работа постоянно действующих сил также определяется независящей от пути разностью потенциалов этих сил в начальном и конечном состояниях системы, эти функции называются термодинамическими потенциалами. В зависимости от условий протекания процесса различают четыре термодинамических потенциала.

1) При V, S = const уравнение (2.40) принимает вид

т. е. внутренняя энергия является изохорно-изоэнтропийным потенциалом.

2) При р, S = const из уравнения (2.40) находим, что

т. е. энтальпия является изохорно-изоэнтропийным потенциалом.

Большинство реальных процессов протекают в условиях, когда S ≠ const и dS ≠ 0. Поэтому с практической точки зрения наибольший интерес представляют изохорно-изотермический и изобарно-изотермический потенциалы.

3) При V, Т = const уравнение (2.40) принимает вид

где величина F = U – TS: является свойством системы; она называется энергией Гельмгольца (функция введена Гельмгольцем в 1882 г.) или изохорно-изотермическим (изохорным) потенциалом. Очевидно, что

Исходя из определения энергии Гельмгольца и уравнения (3.28) получим

Следовательно F является функцией температуры и объема системы: F = f(T, V). Тогда

Сравнивая (2.46) и (2.45), получим

Соотношение (2.49) называется третьим уравнением Максвелла.

Объединяя (2.44) и (2.47) получим уравнение Гиббса-Гельмгольца для зависимости ΔF от температуры:

4) При p, Т = const уравнение (2.40) принимает вид

где величина G = U – TS + pV = H – TS = F + pV: является свойством системы; она называется энергией Гиббса (функция введена Гиббсом в 1875 г.) или изобарно-изотермическим (изобарным) потенциалом. Очевидно, что

Исходя из определения энергии Гиббса и уравнения (2.28), получим

Таким образом, G = f(T, р)есть характеристическая функция системы:

Сравнивая (2.54) и (2.53), получим

Соотношение (2.57) является четвертым уравнением Максвелла.

Объединяя (2.57) и (2.52) получим уравнение Гиббса-Гельмгольца для зависимости ΔG от температуры:

Любой термодинамический потенциал в необратимых процессах при постоянстве естественных переменных уменьшается и достигает минимума при равновесии. Таким образом, все мыслимые процессы в системах охватываются соотношением:

где знак равенства относится к состоянию равновесия; знак «

Дата добавления: 2015-09-29 ; просмотров: 3453 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ