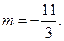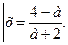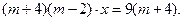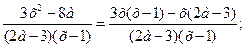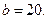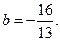Уравнения приводимые к линейным примеры

Решение простых линейных уравнений

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

−4x = 12 | : (−4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Перенести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

1. 4х + 8 = 6 − 7х
2. 4х + 7х = 6 − 8
3. 11х = −2
4. х = −2 : 11
5. х = −2/11

Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.

Пример 5. Решить:

1. 
2. 3(3х — 4) = 4 · 7х + 24
3. 9х — 12 = 28х + 24
4. 9х — 28х = 24 + 12
5. -19х = 36
6. х = 36 : (-19)
7. х = — 36/19

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

5х — 15 + 2 = 3х — 2 + 2х — 1

Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

Приведем подобные члены.

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 − 7х.

II. Линейные уравнения с параметрами уравнения приводимые к линейным

Оглавление

II. Линейные уравнения с параметрами уравнения приводимые к линейным. 4

III. Примеры простейших линейных уравнений с параметром. 6

IV. Линейные уравнения с параметром, имеющие стандартный канонический вид 9

V. Уравнения, приводимые к линейным уравнениям с параметром. 111

I. Введение

Уравнения и неравенства с параметрами являются традиционно наиболее трудными задачами курса математики. Чаще всего они встречаются в заданиях повышенной сложности, а также ученики довольно часто сталкиваются с такими заданиями на ОГЭ и ЕГЭ. В прошлом году только 13,4 % девятиклассников смогли выполнить задание 23 части С. На следующий год нам тоже предстоит сдавать ОГЭ, а данная тема вызывает наибольшее затруднение. Именно поэтому мы выбрали эту тему.

Цель

Изучение решения линейных уравнений с параметрами.

Задачи

1.Познакомиться с понятием параметра.

2.Изучить общий принцип и метод решения линейных уравнений с параметрами.

3.Рассмотреть различные виды уравнений с параметрами.

4.Научиться решать уравнения с параметрами.

Актуальность

Тема «Решение и исследование уравнений с параметрами» присутствует в материалах ОГЭ и Единого государственного экзамена. Данная тема является одной из самых трудных в курсе алгебры.. Совершенно очевидно, что к «встрече» с такими задачами надо специально готовиться.

Предмет исследования:линейные уравнения с параметром.

Объект исследования:алгоритм решения линейных уравнений с параметрами.

II. Линейные уравнения с параметрами уравнения приводимые к линейным

Параметр (от греческого “parametron” – отмеривающий) – величина, значения которой служат для различения элементов некоторого множества между собой. С использованием параметров проводятся исследования многих систем и процессов реальной жизни. В частности, в физике в качестве параметров могут выступать температура, время и др. В математике параметры вводятся для обозначения некоторой совокупности объектов. Так, уравнение + = с параметрами а, b и с определяет совокупность всех окружностей; уравнение + = 1 – всех единичных окружностей; уравнение + = – совокупность концентрических окружностей с центром в начале координат. Рассмотрим с точки зрения алгебры, как определяется уравнение с параметром.

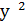
Определение.Уравнение вида Аx=В , где А и В зависят от параметра, то есть А=А(а), В=В(а) называется линейным уравнением с параметром а.

Замечание. Уравнение, которое с помощью тождественных преобразований сводится к уравнению Аx=В, также называется линейным.

Более примитивно линейное уравнение с параметром определяется как уравнение, в запись которого, кроме неизвестных, входят числа, обозначенные буквами.

В отношении уравнений с параметром чаще всего встречаются две постановки задачи:

1) Для каждого значения параметра найти все решения заданного уравнения;

2) Найти все значения параметра, при каждом из которых решения урав- нения удовлетворяют заданным требованиям.

В качестве примера рассмотрим уравнение

1) Пусть , тогда уравнение примет вид

Решим его:

2) Пусть , тогда уравнение примет вид , решением которого является любое действительное значение .

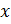
3) Пусть , тогда уравнение примет вид . Решив его, получим, что . В этом случае уравнение не имеет решения.

Следовательно, сам факт существования решения зависит от значения

параметра .

Определение. Исследовать и решить уравнение с параметром это значит :

— найти все системы значений параметров, при которых данное уравнение имеет решение;

— найти все решения для каждой найденной системы значений параметров, т.е. для неизвестного и параметра должны быть указаны свои области допустимых значений.

Уравнения, приводимые к линейным.

Несложные уравнения с параметром, при решении которых требуется дополнительная проверка, связанная с ограничениями их области определения, составляет следующий шаг в изучении уравнений с параметром.

Пример1. Решите уравнение

Решение. Очевидно, что х ≠ 2. Умножив обе части уравнения на х–2≠0, получим а = х – 2 или х = а + 2. Проверим, нет ли таких значений параметра а, при котором найденное значение х было бы равно числу 2, то есть решим уравнение 2 = а + 2 относительно а. Получим, что при а = 0 х =2, но число 2 не входит в область определения, следовательно, не может быть его корнем.

Ответ: при а = 0 корней нет; при а≠ 0 х = а +2.

Пример2. Решите уравнение

Решение: х ≠ –1. Приведя уравнение к виду (1 — а)х = а, заметим, что при а = 1 уравнение не имеет корней, а при а ≠1 получаем . Решим уравнение относительно а. Так как уравнение не имеет корней, других вариантов не имеется.

Ответ: при а ≠1 ; при а = 1 корней нет.

Пример 3. Решите уравнение

Решение При условии, что исходное уравнение можно упростить:

После преобразований получаем уравнение 2ах =1– а, которое при а = 0 не имеет корней, а при а ≠ 0 . Проверим, нет ли таких значении параметра а, при которых найденное значение х было бы равно – 3 или 2. для этого решим относительно а уравнения . Корень первого уравнения

– 0,2, корень второго уравнения 0,2, то есть при а ± 0, 2 соответствующие значения х не входят в область определения исходного уравнения.

Ответ: при корней нет; при .

Пример 4. Исследовать и решить уравнение с параметром.

kx + 2k – 3k + 3 = x + 1;

(k – 1 )x = x + 1 — вид уравнения наиболее удобный для исследования.

a) Пусть k ≠ 1, тогда существует единственный х .

б) Выясним, при каких значениях параметра k х = -1, и исключим их.

Для этого решим уравнение:

, тогда k = 1,5.

в) Если k = 1, то 0х = -1, решений нет.

Графическая иллюстрация исследования по параметру k

1) 2) 3)

Ответ: 1) При k ≠ 1

k ≠1,5 существует ед. х = .

2) При k =1 решений нет.

3) При k = 1,5 решений нет.

Пример 5. Исследовать и решить уравнение с параметром.

D (у): m ≠ 1

Преобразуем данное уравнение в равносильное с учётом D (у):

3mx – 5 + (3m – 11)(x + 3) = (2x + 7)(m – 1);

(4m – 9)x = 31 – 2m — линейное уравнение с параметром, удобное для исследования.

а) Если m ≠ 2,25

m ≠ 1 , то существует ед.

б) Выясним, при каких значениях параметра m x = -3.

следовательно, m = — 0,4, т.е. при m = — 0,4 х .

в) Если m = 2,25, то 0х = 26,5, следовательно, решений нет.

Графическая иллюстрация исследования по параметру

Ответ: 1) при m ≠ 2,25

m ≠ — 0,4 существует ед.

2) При m = 2,25 решений нет

3) При m = — 0,4 решений нет

4) При m = 1 уравнение не определено или не имеет смысла.

Пример 6. Исследовать и решить уравнение с параметром.

D(y): Выполнив необходимые преобразования получим следующее уравнение:

.

а) Если то

б) тогда т.е.

в) тогда т.е.

г) тогда 0= — 6,5, следовательно, решений нет

Графическая иллюстрация исследования c параметром m

— 2 -1,5

Ответ: 1) При существует единственное решение

2) При решений нет

3) При решений нет

4) При уравнение не определено.

5) При решений нет.

Пример 7. Исследовать и решить уравнение с параметром:

D(y) :

Данное уравнение перепишем в виде

или

а) Если то существует ед.

б) Выясним, при каких значениях параметра m x=1, и исключим эти значения, т.е. или 2 = 1. Следовательно, не существует такого значения параметра m, при котором x=1, т.е. дополнительных ограничений на значение параметра m нет.

в) Если m=1, то, следовательно, любое есть решение уравнения, т.е. это случай бесконечного множества решений.

г) Если m = -1, то , т.е. решений нет.

д) Если m = 0 — уравнение не определено.

Ответ: а) а) Если то существует ед. x

б) Если m=1, то для любого x ≠ 1 есть решение.

в) Если m = -1, решений нет

г) Если m = 0 — уравнение не определено.

Пример 8. Исследовать и решить уравнение с параметром:

Найдём область определения данного уравнения. D(y) : х ≠±1.

Запишем уравнение в виде. или

а) Если а ≠ -2 , то существует ед. х

б) Выясним, при каких значениях параметра а х=1, и исключим их.

, т.е. а = 1.

в) выясним, при каких значениях параметра а х=-1,

, т.е. 4=-2, или решений нет. Следовательно, не существует такого значения параметра а, при котором х=-1.

г) Если а = -2, то , т.е. решений нет.

Графическая иллюстрация исследования c параметром а

-2 1

Ответ 1) При 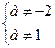существует ед. х

2) При а = -2, решений нет.

3) При а = 1, решений нет.

Пример 9. Исследовать и решить уравнение с параметром

D(y): .

Запишем уравнение в виде , или

а) Если то существует ед. х

б) Выясним, при каких значениях параметра m x=-3.

т.е. m ≠-1.

в) Если m = -4, то , следовательно, любое х из области определения уравнения есть решение.

г) Если m = 2, то , т.е решений нет.

д) Если m = -1 – уравнение не определено.

Ответ: 1) При то существует ед. х

2) При m = — 4, любое х ≠-3 есть решение.

3) При m = 2, решений нет.

4) При m = -1 – уравнение не определено

Пример 10. Исследовать и решить уравнение с параметром

D (y): .

Запишем уравнение в виде

а) Если то существует ед. х .

б) Если а=0, то 0=0, следовательно, любое х из области определения есть решение.

Ответ: 1) При то существует ед. х .

2) При а=0, любое х ≠ 1 – есть решение.

3) При а = 1,5 уравнение не определено.

Пример 11. Исследовать уравнение, выяснить, при каких значениях параметра m существует единственное решение, меньше 1.

D(y):

Запишем уравнение в виде

I. а) Если то существует ед. х

б) Выясним, при каком значении параметра m х=-2.

т.е.

в) Выясним, при каком значении параметра m х=-3

т.е. .

II. Решим неравенство . Перенесём 1 в левую часть, тогда

0 1

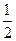
Ответ: при существует единственное решение такое, что .

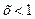
Пример 12. Исследовать уравнение, выяснить при каких значениях параметра m существует единственное положительное решение.

D(y) .

Запишем уравнение в виде .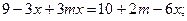

I. а) Если 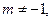то существует ед. х

б) Выясним, при каком значении параметра m

тогда

в) При найдём дополнительное ограничение на значение параметра m.

Тогда уравнение имеет вид

т.е.

II.

-2 -1 -½

Ответ: при существует ед. х

Пример 13. Исследовать и решить уравнение с параметром

D (y):

В результате преобразований получаем — данное уравнение наиболее удобно для исследования.

а) Если то существует ед. х

б) Выясним при каком значении параметра b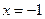

в) Выясним при каком значении параметра b

г) Если , то решений нет.

Ответ: 1)При существует ед. х

2) При решений нет. 3) При решений нет.

4) При решений нет.

Пример 14. Исследовать и решить уравнение с параметром

D(y):

Преобразуем уравнение в более удобное для исследования.

.

а) Если то существует ед х

б) Выясним, при каком значении параметра n х=0.

.

в) Если , то любое значении х из области определения является решением.

г) Если , уравнение не определено.

д) Если , уравнение не определено.

Ответ: 1) При то существует ед. х

2) При любое является решением.

3) При , уравнение не определено.

4) При , уравнение не определено.

Для реализации проекта мною были проанализированы методическая литература и учебные пособия, которые позволили выявить основные методы решения линейных уравнений с параметрами и адаптировать их к школьному курсу. Что помогло составить систему дидактических материалов, которые можно использовать для учащихся 7 – 11 классов в процессе усвоения той или иной темы или для параллельного повторения при подготовке к ГИА или ЕГЭ.

1. Натяганов В.Л., Лужина Л.М. Методы решения задач с параметрами: Учеб. пособие. – М.: Изд-во МГУ, 2003. – 368 с.

2. Шахместер А.Х. Уравнения и неравенства с параметрами. – 1-е изд.– СПб.: «ЧеРо-на-Неве», 2004.– 304с.

3. Шахместер А.Х. Задачи с параметрами в ЕГЭ. –

1-е изд.– СПб.: «ЧеРо-на-Неве», 2004.– 304с.

4. Шахместер А.Х. Задачи с параметрами на экзаменах. – 3-е изд., исправленное.– М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс»,2009. – 248с.

5. Н.Воронина Уравнения с параметрами на уроках повторения. – Газета «Математика» №1/ 2010г. Издательский дом «Первое сентября».

6. Т.Овчинникова, Факультативный курс «Линейные уравнения и неравенства с параметрами» – Газета «Математика» №1/ 2010г. №2/2010, №3/2010 Издательский дом «Первое сентября».

7. П.И. Горнштейн, В.Б. Полонский, М.С. Якир Задачи с параметрами. 3-е издание, дополненное и переработанное. – М.: Илекса, Харьков: Гимназия, 1999 – 336с.

8. Алгебра. 8 класс. В 2 ч. /[А.Г.Мордкович и др.] под ред. А.Г. Мордковича. – 11-е изд. Стер. М.: Мнемозина, 2009.

9. Алгебра. 9 класс. В 2 ч. /[А.Г.Мордкович и др.] под ред. А.Г. Мордковича. – 11-е изд. Стер. М.: Мнемозина, 2009.

10. Алгебра. 10-11 класс. В 2 ч. /[А.Г.Мордкович и др.] под ред. А.Г. Мордковича. – 11-е изд. Стер. М.: Мнемозина, 2009.

11. Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. – 9-е изд.- М.: Айрис-пресс, 2004 – 432с.

12. Субханкулова С.А. Задачи с параметрами. – М.: ИЛЕКСА, 2010. – 208с (Серия «Математика: элективный курс»).