Уравнения прямой и плоскости перпендикуляр

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

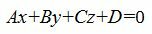(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

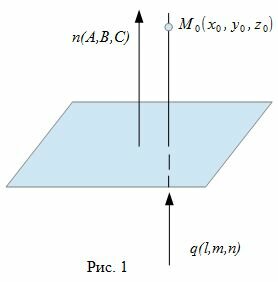Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

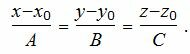(3)

Пример 1. Построить прямую, проходящую через точку M₀(5, -4, 4) и перпендикулярной плоскости

Общее уравнение плоскости имеет вид (1), где :

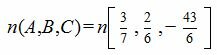(4)

Подставляя координаты точки M₀(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

Перпендикулярные прямая и плоскость, признак и условия перпендикулярности прямой и плоскости

Статья раскрывает понятие о перпендикулярности прямой и плоскости, дается определение прямой, плоскости, графически иллюстрировано и показано обозначение перпендикулярных прямой и плоскости. Сформулируем признак перпендикулярности прямой с плоскостью. Рассмотрим условия, при которых прямая и плоскость будут перпендикулярны с заданными уравнениями в плоскости и трехмерном пространстве. Все будет показано на примерах.

Перпендикулярные прямая и плоскость – основные сведения

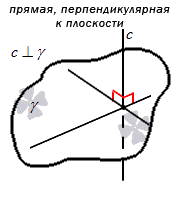
Прямая перпендикулярна к плоскости, когда она перпендикулярна к любой прямой, лежащей в этой плоскости.

Верно то, что и плоскость перпендикулярна к прямой, как и прямая к плоскости.

Перпендикулярность обозначается « ⊥ ». Если в условии задано, что прямая с перпендикулярна плоскости γ , тогда запись имеет вид с ⊥ γ .

Например, если прямая перпендикулярна к плоскости, тогда возможно провести только одну прямую, благодаря которой две смежных стены комнаты пересекутся. Прямая считается перпендикулярной к плоскости потолка. Канат, расположенный в спортзале рассматривается в качестве отрезка прямой, который перпендикулярен плоскости, в данном случае полу.

При наличии перпендикулярной прямой к плоскости, угол между прямой и плоскостью считается прямым, то есть равен 90 градусов.

Перпендикулярность прямой и плоскости – признак и условия перпендикулярности

Для нахождения выявления перпендикулярности необходимо использовать достаточное условие перпендикулярности прямой и плоскости. Оно гарантирует выполнение перпендикулярности прямой и плоскости. Данное условие считается достаточным и называют признаком перпендикулярности прямой и плоскости.

Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, которые лежат в этой плоскости.

Подробное доказательство приведено в учебнике геометрии 10 — 11 класса. Теорема применяется для решения задач, где необходимо установить перпендикулярность прямой и плоскости.

При условии параллельности хоть одной из прямых плоскости, считается, что вторая прямая также перпендикулярна к данной плоскости.

Признак перпендикулярности прямой и плоскости рассматривается еще со школы, когда необходимо решить задачи по геометрии. Рассмотрим подробнее еще одно необходимое и достаточное условие, при котором прямая и плоскость будут перпендикулярны.

Для того, чтобы прямая а была перпендикулярна плоскости γ , необходимым и достаточным условием является коллинеарность направляющего вектора прямой а и нормального вектора плоскости γ .

При a → = ( a x , a y , a z ) являющимся вектором прямой a , при n → = ( n x , n y , n z ) являющимся нормальным вектором плоскости γ для выполнения перпендикулярности нужно, чтобы прямая a и плоскость γ принадлежали выполняемости условия коллинеарности векторов a → = ( a x , a y , a z ) и n → = ( n x , n y , n z ) . Отсюда получаем, что a → = t · n → ⇔ a x = t · n x a y = t · n y a z = t · n z , t является действительным числом.

Данное доказательство основывается на необходимом и достаточном условии перпендикулярности прямой и плоскости, направляющего вектора прямой и нормального вектора плоскости.

Данное условие применимо для доказательства перпендикулярности прямой и плоскости, так как достаточно найти координаты направляющего вектора прямой и координаты нормального вектора в трехмерном пространстве, после чего производить вычисления. Используется для случаев, когда прямая определена уравнением прямой в пространстве, а плоскость уравнением плоскости некоторого вида.

Доказать перпендикулярность заданной прямой x 2 — 1 = y — 1 2 = z + 2 2 — 7 с плоскостью x + 2 2 + 1 y — ( 5 + 6 2 ) z .

Знаменатели канонических уравнений являются координатами направляющего вектора данной прямой. Отсюда имеем, что a → = ( 2 — 1 , 2 , 2 — 7 ) является направляющим вектором прямой x 2 — 1 = y — 1 2 = z + 2 2 — 7 .

В общем уравнении плоскости коэффициенты перед переменными x , y , z являются координатами нормального вектора данной плоскости. Отсюда следует, что n → = ( 1 , 2 ( 2 + 1 ) , — ( 5 + 6 2 ) ) — это нормальный вектор плоскости x + 2 2 + 1 y — ( 5 + 6 2 ) z — 4 = 0

Необходимо произвести проверку выполнимости условия. Получаем, что

2 — 1 = t · 1 2 = t · 2 ( 2 + 1 ) 2 = t · ( — ( 5 + 6 2 ) ) ⇔ t = 2 — 1 , тогда векторы a → и n → связаны выражением a → = ( 2 — 1 ) · n → .

Это и есть коллинеарность векторов. отсюда следует, что прямая x 2 — 1 = y — 1 2 = z + 2 2 — 7 перпендикулярна плоскости x + 2 ( 2 + 1 ) y — ( 5 + 6 2 ) z — 4 = 0 .

Ответ: прямая и плоскость перпендикулярны.

Определить, перпендикулярны ли прямая y — 1 = 0 x + 4 z — 2 = 0 и плоскость x 1 2 + z — 1 2 = 1 .

Чтобы ответить на вопрос перпендикулярности, необходимо, чтобы было выполнено необходимое и достаточное условие, то есть для начала нужно найти вектор заданной прямой и нормальный вектор плоскости.

Из прямой y — 1 = 0 x + 4 z — 2 = 0 видно, что направляющий вектор a → — это произведение нормальных векторов плоскости y — 1 = 0 и x + 4 z — 2 = 0 .

Отсюда получаем, что a → = i → j → k → 0 1 0 1 0 4 = 4 · i → — k → .

Координаты вектора a → = ( 4 , 0 , — 1 ) .

Уравнение плоскости в отрезках x 1 2 + z — 1 2 = 1 является эквивалентным уравнению плоскости 2 x — 2 z — 1 = 0 , нормальный вектор которой равен n → = ( 2 , 0 , — 2 ) .

Следует произвести проверку на коллинеарность векторов a → = ( 4 , 0 , — 1 ) и n → = ( 2 , 0 , — 2 ) .

Для этого запишем:

4 = t · 2 0 = t · 0 — 1 = t · ( — 2 ) ⇔ t = 2 t ∈ R ⇔ t ∈ ∅ t = 1 2

Отсюда делаем вывод о том, что направляющий вектор прямой не коллинеарен нормальному вектору плоскости. Значит, y — 1 = 0 x + 4 z — 2 = 0 — это прямая, не перпендикулярная к плоскости x 1 2 + z — 1 2 .

Ответ: прямая и плоскость не перпендикулярны.

Прямая, перпендикулярная к плоскости.
Признак перпендикулярности прямой и плоскости.
Расстояние от точки до плоскости

Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости

Свойства перпендикуляра к плоскости. Расстояние от точки до плоскости

Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости

Определение . Прямой, перпендикулярной к плоскости , называют такую прямую, которая перпендикулярна к каждой прямой, лежащей на этой плоскости.

Признак перпендикулярности прямой и плоскости . Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в некоторой плоскости, то прямая перпендикулярна к этой плоскости.

Доказательство . Рассмотрим сначала следующий случай.

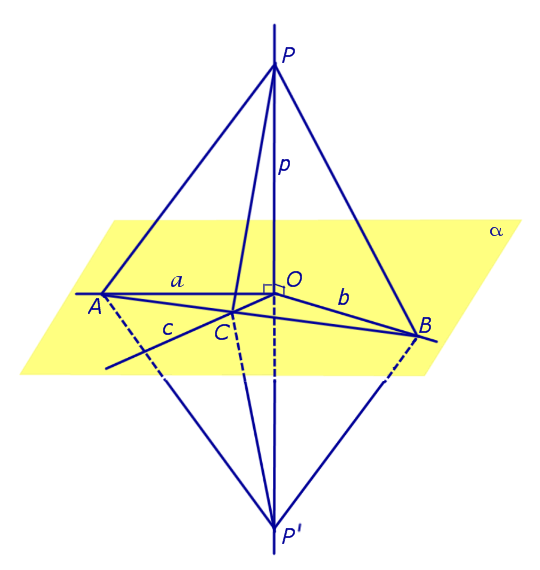
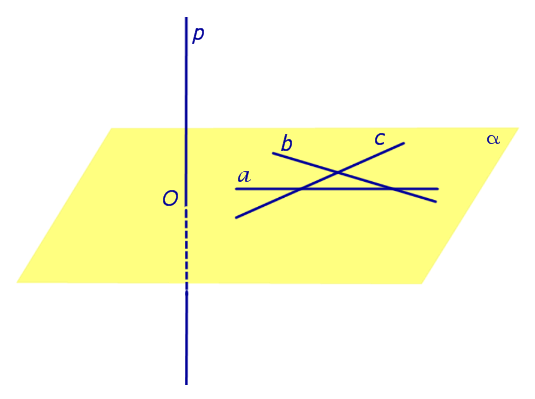
Предположим, что прямая p , пересекающая плоскость α в точке O, перпендикулярна к прямым a и b , лежащим на плоскости α и проходящим через точку O . Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c , лежащей на плоскости α и проходящей через точку O .

С этой целью отметим на прямой a произвольную точку A , а на прямой b произвольную точку B (рис. 1).

Проведем прямую AB и обозначим буквой C точку пересечения прямых AB и c. Отметим на прямой p произвольную точку P и обозначим символом P’ точку, расположенную на прямой p так, чтобы точка O оказалась серединой отрезка PP’ . Поскольку прямые OA и OB являются серединными перпендикулярами к отрезку PP’ , то справедливы равенства

Из этих равенств, а также поскольку отрезок AB является общей стороной треугольников APB и AP’B , заключаем, что в силу признака равенства треугольников по трем сторонам трегольники APB и AP’B равны. Следовательно,

Отсюда в силу признака равенства треугольников по двум сторонам и углу между ними заключаем, что трегольник PBС равен треугольнику P’BС ( BP = BP’ , 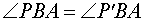, сторона BС — общая). Следовательно,

Таким образом, прямые PO и c перпендикулярны, что и требовалось доказать в рассматриваемом случае.

Теперь перейдем к общему случаю.

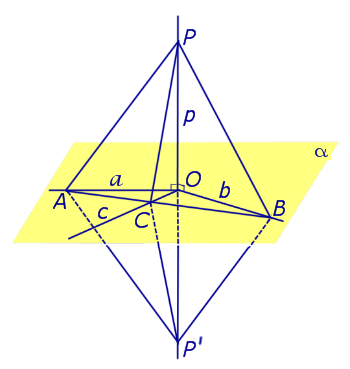
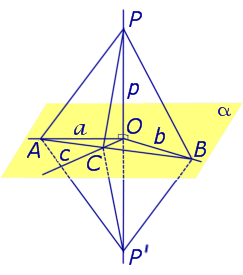
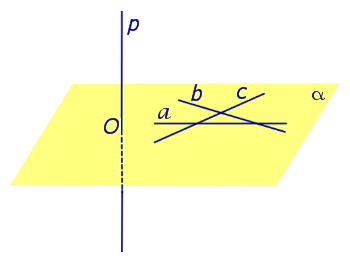
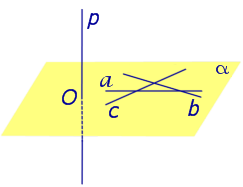
Предположим, что что прямая p , пересекающая плоскость α в точке O, перпендикулярна к прямым a и b , лежащим на плоскости α . Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c , лежащей плоскости α (рис. 2).

С этой целью проведем через точку O прямые a’ , b’ и c’ соответственно параллельные прямым параллельные прямым a , b и c .

По определению угла между скрещивающимися прямыми прямая будет перпендикулярна прямым a’ и b’ , проходящим через точку O, и мы оказываемся в условиях уже рассмотренного случая.

Доказательство признака перпендикулярности прямой и плоскости завершено.

Замечание . Прямую, перпендикулярную к плоскости, часто называют перпендикуляром к плоскости. Точку перечения прямой, перпендикулярной к плоскости, с самой плоскостью называют основанием перпендикуляра.

Так, например, на рисунке 1 точка O является основанием перпендикуляра, опущенного из точки P на плоскость α .

Свойства перпендикуляра к плоскости

Перечислим следующие свойства перпендикуляра к плоскости, доказательства которых мы оставляем читателю в качестве полезных упражнений.

Рисунок	Свойство
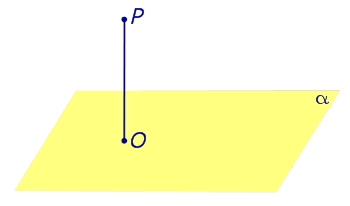
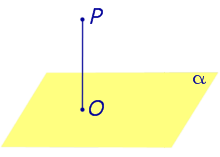
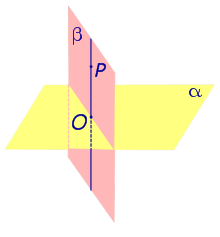
	Из любой точки можно опустить перпендикуляр на любую плоскость. Если точка O — основание перпендикуляра, опущенного из точки P на плоскость α , то длину отрезка PO называют расстоянием от точки P до плоскости α.
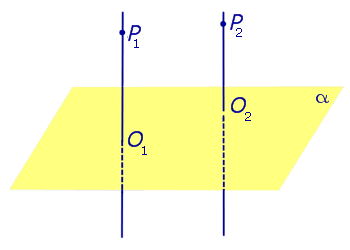
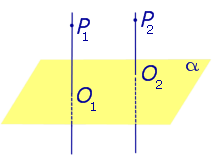
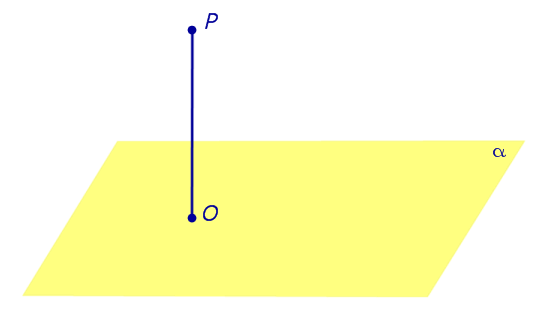
	Два любых перпендикуляра к плоскости параллельны
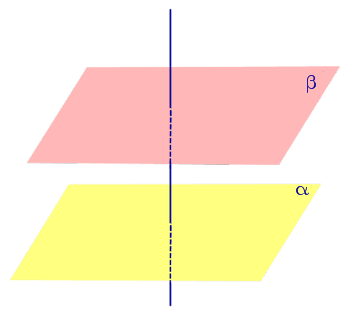
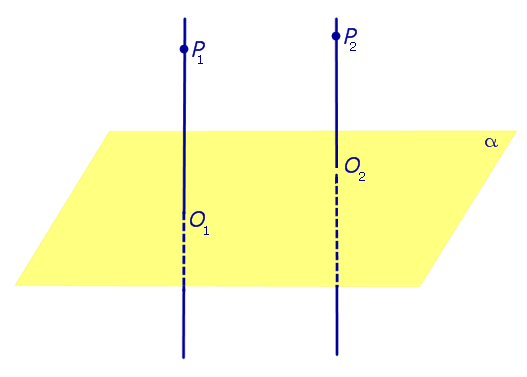
	Плоскости, перпендикулярные к одной прямой, параллельны.
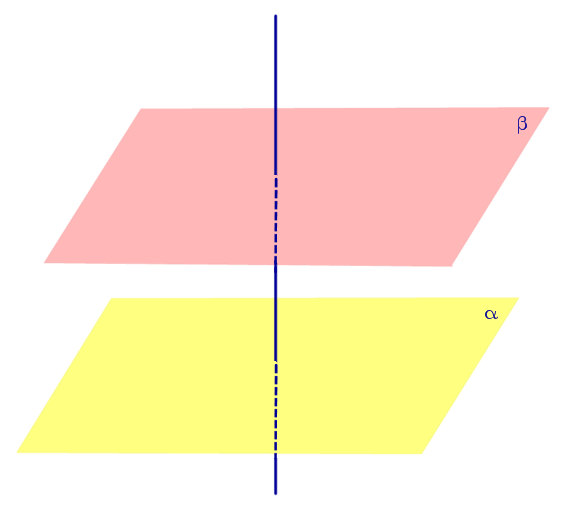
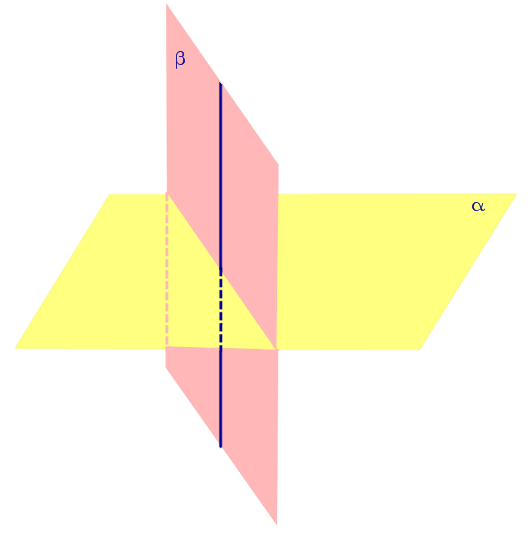	Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны.
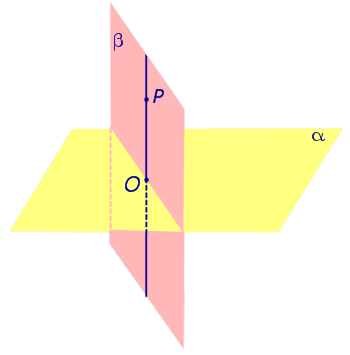
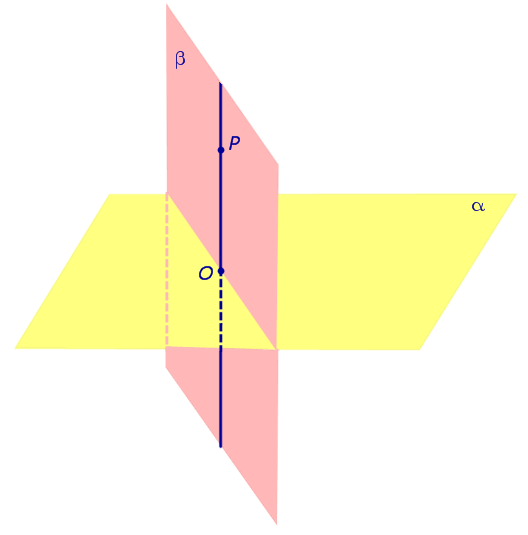	Если плоскости α и β перпендикулярны, а точка P лежит на плоскости β, то и перпендикуляр PO, опущенный из точки P на плоскость α , также лежит в плоскости β.

Свойство:
Из любой точки можно опустить перпендикуляр на любую плоскость. Если точка O — основание перпендикуляра, опущенного из точки P на плоскость α , то длину отрезка PO называют расстоянием от точки P до плоскости α.

Свойство:
Два любых перпендикуляра к плоскости параллельны параллельны

Свойство:
Плоскости, перпендикулярные к одной прямой, параллельны.

Свойство:
Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны.

Свойство:
Если плоскости α и β перпендикулярны, а точка P лежит на плоскости β, то и перпендикуляр PO, опущенный из точки P на плоскость α , также лежит в плоскости β.