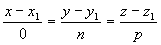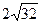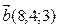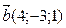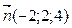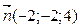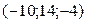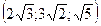Прямые в пространстве. Прямая и плоскость в пространстве.
план-конспект занятия
Прямые в пространстве. Прямая и плоскость в пространстве.
Скачать:
| Вложение | Размер |
|---|---|
| Прямые в пространстве. Прямая и плоскость в пространстве. | 185 КБ |
Предварительный просмотр:
Теоретическое занятие по теме:
Прямые в пространстве. Прямая и плоскость в пространстве.
Маршрутный лист занятия:
1. Запишите конспект в тетрадь. Текст, выделенный желтым цветом, конспектировать НЕ нужно, его необходимо внимательно прочитать и разобрать.
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «стереос» — объемный, пространственный и «метрео» — измерять.
Основные понятия стереометрии
Простейшими и, можно сказать, основными фигурами в пространстве являются точки, прямые и плоскости . Наряду с этими фигурами мы будем рассматривать так называемые геометрические тела и их поверхности . Представление о геометрических телах дают окружающие нас предметы.
Основными понятиями стереометрии являются точка, прямая и плоскость, которые являются идеализациями объектов реального пространства.
Точка является идеализацией очень маленьких объектов, т. е. таких, размерами которых можно пренебречь. Евклид в своей книге «Начала» определял точку как то, что не имеет частей.
Прямая является идеализацией тонкой натянутой нити, края стола прямоугольной формы. По прямой распространяется луч света.
Плоскость является идеализацией ровной поверхности воды, поверхности стола, доски, зеркала и т. п.
Точки будем обозначать прописными латинскими буквами A, B, C,…., прямые — строчными латинскими буквами а, Ь, с , . плоскости — греческими 

Точки, прямые и плоскости будем изображать, как показано на рисунке 1.
Рис. 1
Обратим внимание на то, что прямая является бесконечной, а мы изображаем лишь конечный участок прямой — отрезок, который можно продолжать в обе стороны. Плоскость также является бесконечной, и мы будем изображать лишь ее конечный участок.
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
А 
В 


С 
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
АB 
Прямая АВ лежит в плоскости
Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
а 

Прямая а и плоскость 
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.





Следствие 1. Через прямую a и не лежащую на ней точку A проходит плоскость, и притом только одна.

Рис. 6
Следствие 2. Через две пересекающиеся прямые a и b проходит плоскость, и притом только одна.
Взаимное расположение прямых в пространстве
Возможны три случая взаимного расположения двух прямых в пространстве (Рис. 8):
а) прямые пересекаются, т. е. имеют только одну общую точку (рис. а);
б) прямые параллельны, т. е. лежат в одной плоскости и не пересекаются (рис.б);
в) прямые скрещивающиеся, т. е. не лежат в одной плоскости (рис. в).
Обязательно запомнить обозначения!
Пересекающиеся прямые обозначают так: a 

Параллельные прямые обозначают так: a 

Скрещивающиеся прямые обозначают так: a ∸ b
Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Параллельность прямой и плоскости.
Если две точки прямой лежат в данной плоскости, то по аксиоме 2 вся прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:
а) прямая лежит в плоскости
б) прямая и плоскость имеют только одну общую точку, т. е. пересекаются
в) прямая и плоскость не имеют ни одной общей точки.
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Параллельность прямой а и плоскости α обозначается так: а ∥ 𝛼 . Наглядное представление о прямой, параллельной плоскости, дают натянутые троллейбусные или трамвайные провода — они параллельны плоскости земли. Другой пример дает линия пересечения стены и потолка — эта линия параллельна плоскости пола.
Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Доказательство. Рассмотрим плоскость а и две параллельные прямые а и b, расположенные так, что прямая b лежит в плоскости а, а прямая а не лежит в этой плоскости (Рис. 9).
Докажем, что а ∥ 𝛼 .. Допустим, что это не так. Тогда прямая а пересекает плоскость а, а значит, по лемме о пересечении плоскости параллельными прямыми прямая b также пересекает плоскость а. Но это невозможно, так как прямая
b лежит в плоскости а. Итак, прямая а не пересекает плоскость а, поэтому она параллельна этой плоскости. Теорема доказана.
Запишем еще два утверждения , которые часто используются при решении задач.
1°. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
2°. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Параллельные прямые в пространстве.
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Параллельность прямых а и b обозначается так: а ∥ 𝑏 . Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Доказательство. Рассмотрим прямую а и точку М, не лежащую на этой прямой (Рис. 1о). Через прямую а и точку М проходит плоскость, и притом только одна (п. 3). Обозначим эту плоскость буквой а. Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т. е. должна лежать в плоскости а. Но в плоскости а, как известно из курса планиметрии, через точку М проходит прямая, параллельная прямой а, и притом только одна. На рисунке эта прямая обозначена буквой b. Итак, b — единственная прямая, проходящая через точку M параллельно прямой а. Теорема доказана.
Перпендикулярные прямые в пространстве.
Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°. Перпендикулярность прямых а и b обозначается так: a ⊥ 𝑏 . Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.
Лемма. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Окружающая нас обстановка дает много примеров, иллюстрирующих перпендикулярность прямой и плоскости. Не покосившийся телеграфный столб стоит прямо, т. е. перпендикулярно к плоскости земли. Так же расположены колонны здания по отношению к плоскости фундамента, линии пересечения стен по отношению к плоскости пола и т. д.
Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Теорема (O). Если две прямые перпендикулярны к плоскости, то они параллельны.
Признак перпендикулярности прямой и плоскости.
Как проверить, перпендикулярна ли данная прямая к данной плоскости? Этот вопрос имеет практическое значение, например, при установке мачт, колонн зданий и т. д., которые нужно поставить прямо, т. е. перпендикулярно к той плоскости, на которую они ставятся. Оказывается, что для этого нет надобности проверять перпендикулярность по отношению к любой прямой, как о том говорится в определении, а достаточно проверить перпендикулярность лишь к двум пересекающимся прямым, лежащим в плоскости. Это вытекает из следующей теоремы, выражающей признак перпендикулярности прямой и плоскости.
Теорема. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Перпендикуляр и наклонная
Рассмотрим плоскость α и точку А, не лежащую в этой плоскости. Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью а (Рис. 11).
Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости а, а точка Н — основанием перпендикуляра. Отметим в плоскости а какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости а, а точка М — основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость а. Сравним перпендикуляр АН и наклонную AM: в прямоугольном треугольнике АМН сторона АН — катет, а сторона AM— гипотенуза, поэтому АН
Когда мы говорим, что некоторый предмет, например лампочка уличного фонаря, находится на такой-то высоте, скажем, 6 м от земли, то имеем в виду, что расстояние от лампочки до поверхности земли измеряется по перпендикуляру, проведенному от лампочки к плоскости земли.
Теорема о трех перпендикулярах.
Теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Доказательство. Обратимся к рисунку, на котором отрезок АН — перпендикуляр к плоскости a, AM —наклонная, а — прямая, проведенная в плоскости а через точку М перпендикулярно к проекции НМ наклонной. Докажем, что a ⊥ AM. Рассмотрим плоскость АМН. Прямая а перпендикулярна к этой плоскости, так как она перпендикулярна к двум пересекающимся прямым АН и МНа ⊥ HM по условию и a ⊥ AH, так как АН ⊥ 𝛼 ). Отсюда следует, что прямая а перпендикулярна к любой прямой, лежащей в плоскости АМН, в частности a ⊥ AM. Теорема доказана.
Эта теорема называется теоремой о трех перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами АН, НМ и AM.
Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
2. Рассмотрим следующую задачу (записать в тетрадь):
Точка D не лежит в плоскости треугольника ABC, точки М, N и Р — середины отрезков DA, DB и DC соответственно, точка К лежит на отрезке BN. Выясните взаимное расположение прямых: a) ND и АВ; б) РК и ВС; в) MN и АВ; г) МР и АС; д) KN и AC; е) MD и ВС.
Посмотреть видео-разбор, законспектировать.
3. Вопросы для самоконтроля (ответить устно):
- Дать определение стереометрии?
- Какие основные фигуры в пространстве вы знаете?
- Как обозначаются основные фигуры в пространстве (точка, прямая, плоскость)?
- Какие аксиомы стереометрии и следствия из них вы знаете?
4. Домашнее задание (письменно):
1. Перечислите известные вам аксиомы стереометрии.
2. Дан куб 
В каких плоскостях лежат прямые:
3. Назовите прямые, по которым пересекаются плоскости:
Конспект урока по геометрии на тему «Уравнение прямой»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Тема урока: Уравнение прямой. Угол между прямыми. Условия параллельности и перпендикулярности прямых.
1.Актуализация опорных знаний учащихся
1.Формула расстояния между двумя точками
2.Формула скалярного произведения векторов
3.Формула для вычисления координат вектора
4.Как найти сумму векторов (в координатах)
5.Как с помощью скалярного произведения определить вид угла между векторами?
1.Как найти длину вектора
2.Координаты середины отрезка
3.Формула для нахождения угла между векторами
4.Как найти произведение вектора на число
5. Условие перпендикулярности двух векторов
2. Изучение нового материала
Определение 8.1. Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором .
называемые каноническими уравнениями прямой в пространстве.
В частности, если требуется получить уравнения прямой, проходящей через две точки:

— уравнения прямой, проходящей через две данные точки .
Пример. Составим канонические уравнения прямой 
Будем искать точку на прямой с координатой z 0 =0. Для координат х 0 и у 0 получим систему уравнений 

Угол между прямыми. Угол между прямой и плоскостью.
Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида



Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:


3. Формирование практических умений и навыков:
1.Дан треугольник АВС, А(-2;0;1), В(4;4;1), С(2;-2;1). Найдите длину медианы АМ.
2.Даны точки А, В и С. А(0;5;-8), В(2;-2;0), ), С(3;0;-5). Найдите скалярное произведение векторов АВ и АС
3.Дан треугольник АВС, А(-1;2;1), В(2;-1;1), С(0;-2;1). Найдите косинус угла ВАС.
4.Перпендикулярны ли векторы: <2;-1;-2>, <0;4;-1>?
5. Даны точки А, В, С и D . D(2;4;1), А(0;5;-8), В(2;-2;0), ), С(3;0;-5). Найдите скалярное произведение векторов АD и АС
6.Дано: M(-4;7;0), N(0;-1;2), C – середина MN. Найти: расстояние от начала координат до точки C.
Решение: Сначала найдем координаты точки C. Ее координаты равны полусумме соответствующих координат. 
Нужно найти расстояние от начала координат до точки C. Это значит, что мы должны найти длину отрезка OC или модуль вектора 



Ответ: 
7.Найти координаты вектора 



Вектор 



Так как 






Векторы 


а) Рассмотрим векторы 

Координаты вектора 



б) Рассмотрим векторы 

Координаты вектора 


4. Самостоятельная работа
по теме «Простейшие задачи в координатах»
1.Даны точки А(5; — 2;1) и В(-3; 4; 7).
а)Найдите координаты середины отрезка АВ.
б)Найдите координаты точки С, если точка А – середина отрезка СВ.
2.Даны векторы и Найдите:
в) угол между векторами
3.Даны точки А(2;1;-8), В(1;-5;0), С(8;1;-4). Докажите, что треугольник АВС – равнобедренный.
по теме «Простейшие задачи в координатах»
1.Даны точки А(- 2; 3; 4) и В(4; -1; 6).
а)Найдите координаты середины отрезка АВ.
б)Найдите координаты точки С, если точка В – середина отрезка АС.
2.Даны векторы и Найдите:
в) угол между векторами
3.Даны точки А(-1;5;3), В(-1;-3;9), С(3;-2;6). Докажите, что треугольник АВС – прямоугольный.
Конспект урока Уравнение прямой и плоскости
КГУ «Индустриально-технологический колледж»
Поурочный план № 147-148
Уравнение плоскости и прямой в пространстве. Контрольная работа 12.
Наименование дисциплины: Математика
Подготовил педагог: Тихоненко С.А.
Дата урока: 22.04.2021 года
1. Общие сведения
1.1 Курс, группы: первый, 9СЛ20, 9МК20, 9ОП20
1.2 Тип занятия: комбинированный/ дистанционный
1.3 Межпредметные связи: физика, черчение.
Познакомить учащихся с понятием уравнения плоскости и её особыми случаями задания; Выработать практические навыки по изучаемой теме при решении задач.
познакомить учащихся с понятием уравнение плоскости и алгоритмами составления уравнения плоскости;
дать представление об особых случаях уравнения;
сформировать знания по изучаемой теме
выработать умение применять полученные знания при решении конкретных практических задач.
продолжить формирование навыков самостоятельной работы с информацией;
учить анализировать информацию, обобщать, делать выводы;
развивать умение работать в группах.
воспитывать уважительное отношение к мнению других, умение слушать и слышать окружающих;
способствовать формированию и развитию культуры учащихся, повышению уровня познавательного интереса к предмету;
продолжить работу по формированию положительной мотивации к учебной деятельности;
формировать позитивную психологическую атмосферу в группе.
2.2 Результаты обучения:
1) Усвоить определение вектора и действий с векторами в пространстве.
2.3 Критерии оценки:
1) Выполняет сложение и вычитание векторов, умножение вектора на число;
2)Находит скалярное произведение векторов.
3. Оснащение занятия
3.1 Учебно-методическое оснащение: дидактические материалы, справочно-инструктивные таблицы, карточки с заданиями, оценочные листы .
Справочная литература : А.Е.Әбылқасымова, В.Е. Корчевский, З.Ә. Жумагулова, Алгебра и начала анализа: Учебник для 10 классов естественно- математического направления обшеобразовательных школ.1-2 часть. Алматы: Мектеп, 2019г.
3.2 Техническое оснащение, материалы, ИКТ: мультимедийный проектор, ноутбук, экран.
рованные этапы урока, время
Деятельность, запланированная на уроке
Проверка домашнего задания.
Устный опрос по теме «Координаты вектора в пространстве».
Всякое уравнение первой степени относительно координат x, y, z
Ax + By + Cz +D = 0 (3.1)
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.
Особые случаи уравнения (3.1):
1. D = 0, Ax+By+Cz = 0 — плоскость проходит через начало координат.
2. C = 0, Ax+By+D = 0 — плоскость параллельна оси Oz.
3. C = D = 0, Ax +By = 0 — плоскость проходит через ось Oz.
4. B = C = 0, Ax + D = 0 — плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями:
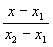
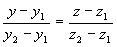
3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
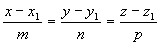
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор a называется направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:
Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:
x = mz + a, y = nz + b. (3.6)
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
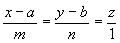
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n1, n2], где n1(A1, B1, C1) и n2(A2, B2, C2) — нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система
равносильна системе 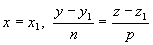
Система 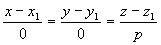
Презентация к уроку.
Пример 1. . Cоставьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение. По условию задачи вектор ОА(1,-1,3) является нормальным вектором плоскости, тогда ее уравнение можно записать в виде
x-y+3z+D=0. Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: 1-(-1)+3×3+D = 0 , D = -11. Итак, x-y+3z-11=0.
1. Написать конспект.
2. Ответить на вопросы теста.
5.Рефлексия по занятию
— Понравился ли вам урок?
— Что было трудным для вас?
— Что вам больше понравилось?
6. Домашнее задание
Ответить на вопросы теста.
Тест по теме «Векторы и координаты в пространстве»
1. Даны точки А(4; 5; 1) и В(0; 9; -8). Чему равна длина отрезка АВ?
a ) 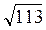
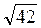
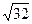
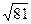
2. Укажите пару коллинеарных векторов:
a ) 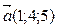
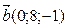
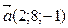
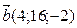
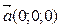
d ) 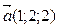
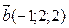
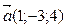
3. Могут ли векторы быть коллинеарными, но не равными?
a ) да b ) нет c ) не достаточно данных
4. Вектор 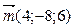
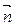
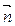
a ) 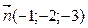
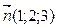
d ) 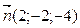
5. Вычислить координаты середины отрезка АВ, если А(-10; 2; 3) и В(0; 16; -7).
a ) 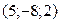
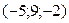
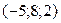
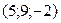
6. Чему равен модуль вектора 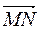
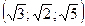
a) 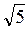
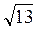
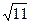
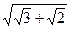
7. При каком положительном n векторы 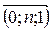
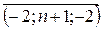
a ) -2; 1 b ) 1 c ) 1; 2 d ) 2 e ) -2
8. Вычислить скалярное произведение векторов 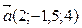
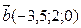
a ) -14 b ) 4 c ) -4 d ) 10 e ) -10
9. Вычислить угол между векторами 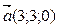
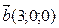
a ) 45˚ b ) 60˚ c ) 30˚ d ) 90˚ e ) 120˚
10. Даны векторы 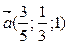
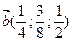
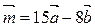
a ) 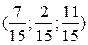
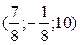
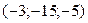
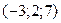
http://infourok.ru/konspekt-uroka-po-geometrii-na-temu-uravnenie-pryamoy-2648968.html
http://znanio.ru/media/konspekt-uroka-uravnenie-pryamoj-i-ploskosti-2708631