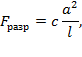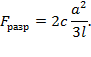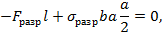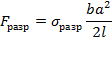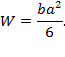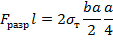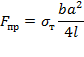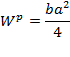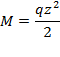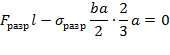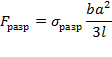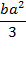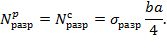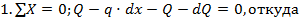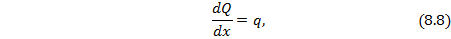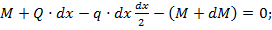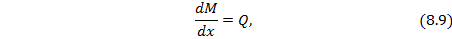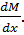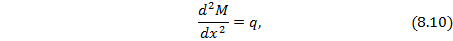Техническая механика
Сопротивление материалов
Изгиб
Дифференциальные зависимости при изгибе
Между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки существуют дифференциальные зависимости, основанные на теореме Журавского , названной по имени русского инженера-мостостроителя Д. И. Журавского (1821-1891 г.г.).
Эта теорема формулируется так:
Поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки.
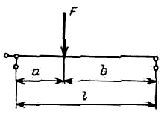
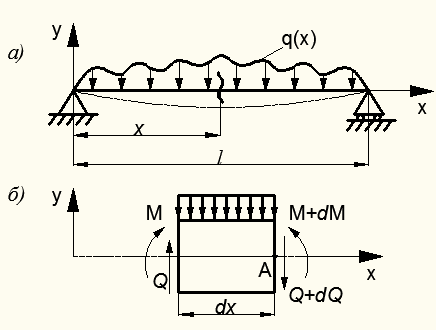
Рассмотрим балку (рис. 1) . Начало координат возьмем на левом конце балки, а ось z направим вправо (в дальнейшем это будет иметь существенное значение).
На одном из участков балки возьмем сечение с текущей координатой z и запишем уравнение изгибающего момента:
Ми = RAz + m – F1 (z – a) + q(z – b) 2 / 2 .
Продифференцировав это выражение по координате z , получим:
Выражение, стоящее в правой части этого равенства, есть поперечная сила Q в сечении z . Таким образом:
теорема доказана.
Если уравнение изгибающих моментов (для участков с равномерно распределенной нагрузкой) продифференцировать вторично, то получим:
d 2 Mи / dz 2 = dQ / dz = q ,
т. е. вторая производная от изгибающего момента или первая производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.
Как известно из высшей математики, по знаку второй производной функции можно судить о выпуклости или вогнутости кривой; соответствующее правило следует использовать при построении эпюр.
Эпюры поперечных сил и изгибающих моментов
Для наглядного изображения распределения вдоль оси балки поперечных сил и изгибающих моментов строят эпюры, которые дают возможность определить предположительно опасное сечение балки и установить значения поперечной силы и изгибающего момента в этом сечении.
Слово «эпюра» в переводе с французского (epure) означает «график» , «чертеж» .
Эпюры поперечных сил и изгибающих моментов можно строить двумя способами.
Первый способ заключается в том, что сначала составляют аналитические выражения поперечных сил и изгибающих моментов для каждого участка, как функций координаты z поперечного сечения:
Затем по полученным уравнениям строят эпюры.
Второй способ заключается в построении эпюр по характерным точкам и значениям поперечных сил и изгибающих моментов на границах участков. Применяя этот способ, в большинстве случаев можно обойтись без составления уравнений поперечных сил и изгибающих моментов.
При наличии некоторого опыта второй способ предпочтительнее.
Правила построения эпюр при изгибе
При построении эпюр следует руководствоваться приведенными ниже правилами:
1. Эпюру моментов строят на сжатом волокне, т. е. положительные моменты (и положительные поперечные силы) откладывают вверх от оси, а отрицательные – вниз;
2. Пользуясь принципом смягченных граничных условий (принципом Сен-Венана) , будем полагать, что в сечении, где приложена сосредоточенная сила (или изгибающий момент), значение поперечной силы (или момента) меняется скачкообразно, причем скачек равен модулю этой силы (или момента);
3. Правильность построения эпюр следует проверять с помощью теоремы Журавского.
Как известно из математики, если Ми =ƒ(z) , то
где α – угол, который составляет касательная к эпюре моментов с положительным направлением оси z .
Согласно теореме Журавского,
Q = dMи / dz = tg α
(полагаем масштабы Ми и z численно равными единице), следовательно, если угол α острый, то Q > 0 и изгибающий момент на участке возрастает, если угол α тупой, то Q и изгибающий момент на участке убывает; если α = 0 на всем участке, то Ми = const , Q = 0 и на этом участке возникает чистый изгиб;
если α = 0 в одной точке эпюры моментов, то в этом сечении Q = 0 , а изгибающий момент имеет экстремальное (максимальное или минимальное) значение.
В сечении, где на эпюре поперечных сил имеется скачок, на эпюре изгибающих моментов будет резкое изменение направления касательной.
Чтобы правила знаков для изгибающих моментов и поперечных сил не противоречили знакам, полученным на основании теоремы Журавского, при проверке эпюр следует ось z мысленно направлять всегда слева направо.
4. На участке, где нет распределенной нагрузки, эпюра моментов представляет собой наклонную прямую, а эпюра поперечных сил – прямую, параллельную оси z .
5. На участке, где приложена равномерно распределенная нагрузка, эпюра моментов представляет собой параболу, а эпюра поперечных сил – наклонную прямую.
6. На конце балки изгибающий момент равен нулю, если там не приложена пара сил.
7. При построении эпюры для консольных балок начало координат удобно брать на конце консоли, что нередко дает возможность обойтись без определения опорных реакций.

Пример построения эпюры поперечных сил и изгибающих моментов приведен на рис. 2 .
Начало координат поместим на левом конце балки, а ось z направим вправо. Данная балка состоит из двух участков. Составив уравнение моментов относительно опор, определим реакции связей (опор). После этого приступаем к построению эпюры поперечных сил, а затем – к построению эпюры изгибающих моментов.
Поскольку к балке не приложена распределенная нагрузка, эпюра сил будет параллельна оси z , а эпюра моментов состоит из наклонных линий, для построения которых достаточно нанести значения моментов для граничных сечений на участках бруса.
На рис.3 представлен пример построения эпюр поперечных сил и изгибающих моментов в балке, к которой приложена распределенная нагрузка.
Как видно из рисунка, эпюра поперечных сил в этом случае – наклонная прямая, эпюра изгибающих моментов – парабола.
Тема 6. Определение напряжений при изгибе прямого стержня
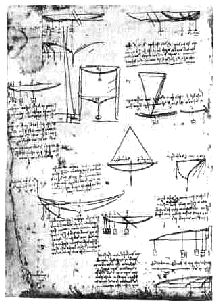
Задача изгиба стержня интересовала еще Леонардо да Винчи . Он установил, что в двухопорной балке постоянного поперечного сечения «изгибается больше всего» та часть, которая находится на наибольшем расстоянии от опор.
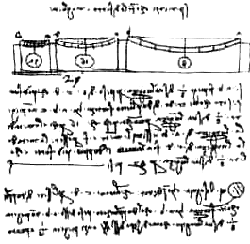
Листы записных книжек Леонардо да Винчи, в которых рассматривается изгиб балок
В результате экспериментальных исследований изгиба балки квадратного поперечного сечения на двух опорах, нагруженной в среднем сечении силой F, Леонардо да Винчи пришел к выводу, что разрушающая сила равна:
F разр = c a 2 l ,
где c — постоянная, a — сторона квадрата, l — длина балки [36]. Если принять, что закон Р.Гука справедлив до разрушения, то тогда правильный результат будет
F разр = 2 c a 2 3 l .
Вероятно, что невысокая экспериментальная техника того времени и наличие пластических деформаций перед разрушением не позволили установить правильный результат. Что касается прогиба, то вначале Леонардо да Винчи получил, что он пропорционален произведению силы на длину балки, затем исправил этот результат, приняв, что он пропорционален произведению силы на квадрат длины и только затем пришел к правильному выводу пропорциональности прогиба произведению силы на куб длины [36].
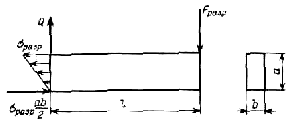
Задача прочности изогнутого прямого стержня прямоугольного поперечного сечения была поставлена Г.Галилеем. На рисунке представлена иллюстрация Галилея к постановке задачи, взятая из его книги [150].
Исследование прочности прямого стержня, проведенное Г.Галилеем
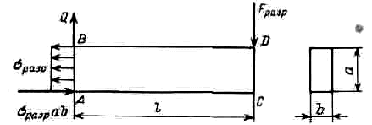
Конечно, Галилей не мог дать правильного решения статически неопределимой задачи изгиба стержня, поскольку ему был неизвестен закон, связывающий напряжения и деформации — закон Гука. Галилей умер, когда Р.Гуку было только семь лет. Да, впрочем, понятия напряжений и деформаций в то время не были определены. Поэтому изложенный ниже анализ решения Галилея является условным. Для решения задачи Галилей принял, что внутренние силы в поперечном сечении изогнутой консольной балки распределены равномерно, т.е. что эпюра напряжений в поперечном сечении является прямоугольником (см. рисунок). Галилей не понимал, что при изгибе стержня часть волокон растянута, а часть сжата. Полагая, что принятое им распределение напряжений имеет место до разрушения, Галилей нашел разрушающую нагрузку из условия равновесия в момент разрушения балки, освобожденной от заделки (сумма моментов относительно оси, проходящей через точку A, на рисунке равна нулю):
Схема распределения напряжений при изгибе балки, принятое Г.Галилеем
— F разр l + σ разр ba a 2 =0,
где F разр — сила, разрушающая балку; σ разр — напряжение при разрушении растянутого стержня из того же материала; b — ширина; a — высота поперечного сечения. Разрушающая нагрузка
F разр = σ разр b a 2 2 l
По сути дела, Галилей рассматривал условие равновесия рычага с точкой опоры A. Таким образом, приняв неверное распределение внутренних сил в поперечном сечении, Галилей ошибся в величине момента сопротивления изгибу в три раза. Как известно, момент сопротивления изгибу прямоугольного поперечного сечения, подсчитанный в предположении справедливости закона Гука, равен
W = b a 2 6 .
Однако если определять предельную нагрузку такую, при которой во всех точках поперечного сечения напряжения равны пределу текучести, то тогда получим
F разр l =2 σ т ba 2 a 4
F пр = σ т b a 2 4 l
т.е. в этом случае так называемый «пластический» момент сопротивления
W p = b a 2 4
и тогда Галилей ошибся уже только в два раза.
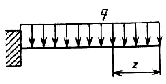
На основании вышеизложенного Галилей пришел к правильному заключению, что стержень прямоугольного поперечного сечения с различными размерами сторон более прочен, когда он поставлен на ребро, нежели когда он лежит плашмя, и во столько раз, во сколько одна сторона больше другой. В случае нагружения консольной балки равномерно распределенной нагрузкой (собственный вес) Галилей пришел к заключению, что изгибающий момент пропорционален квадрату расстояния от свободного конца
M = q z 2 2
где q — интенсивность распределенной нагрузки (вес единицы длины балки).
Для круглого поперечного сечения Галилей правильно установил, что момент сопротивления изгибу пропорционален кубу диаметра, исходя из того, что он должен быть пропорционален произведению площади на диаметр.
Галилей впервые поставил и решил задачу оптимального проектирования. Он нашел закон изменения высоты консольной балки, нагруженной сосредоточенной силой, равного сопротивлению изгибу, т.е.такой балки, у которой во всех поперечных сечениях напряжения одинаковы. Поскольку в основе всех исследований изгиба у Галилея лежало предположение о равномерном распределении напряжений, а закон изменения изгибающего момента (линейный) он принимал правильно, Галилей установил зависимость высоты поперечного сечения от расстояния от свободного конца с точностью до постоянного множителя.
Исследуя изгиб балки на двух опорах, Галилей показал, что наибольший изгибающий момент пропорционален произведению расстояний от точки приложения силы до опор ab, и, следовательно, наибольшая величина момента имеет место в том случае, когда сила приложена в среднем сечении балки.
Изучая прочность полых балок, Галилей пришел к правильному заключению, что при одинаковом весе полые стержни прочнее сплошных.
К решению задачи изгиба балки прямоугольного поперечного сечения вплотную подошел Э.Мариотт и только досадная ошибка не позволила ему вывести правильную формулу для определения нормальных напряжений в балках. Исследование Мариотта по изгибу стержня изложено в его труде, посвященном движению жидкостей [426], опубликованном после его смерти в 1686г.
Схема распределения напряжений при изгибе балки, принятое Э.Мариоттом
Э.Мариоттом независимо от Р.Гука был установлен закон прямой пропорциональности удлинений растянутого образца от приложенной силы, он не понял статическую неопределимость задачи и не использовал установленный им закон при решении задачи изгиба консольной балки прямоугольного поперечного сечения. Вначале Мариотт, так же как и Галилей, полагал, что все волокна балки растянуты, но в отличие от Галилея считал, что закон изменения внутренних сил в поперечном сечении линейный, причем нейтральная линия проходит через нижние точки поперечного сечения. Тогда уравнение имеет вид
F разр l — σ разр b a 2 ∙ 2 3 a =0
F разр = σ разр b a 2 3 l
и, следовательно, момент сопротивления изгибу равен
b a 2 3
т.е. в этом случае Мариотт ошибся в величине момента сопротивления изгибу в два раза. Если считать, что линейный закон распределения внутренних сил справедлив до разрушения, то тогда нагрузка, разрушающая балку, по Мариотту составляет 2/3от нагрузки по Галилею.
Такую же треугольную эпюру напряжений принимали Г.Лейбниц [422] и П.Вариньон [491]. Заметим, что Лейбниц связывал удлинения с внутренними силами при помощи закона Гука.
В дальнейшем Э.Мариотт понял, что при изгибе балки прямоугольного поперечного сечения не все волокна балки растянуты, а половина их сжата, т.е. эпюра нормальных напряжений в поперечном сечении такая, как изображено на рисунке.
Второй вариант схемы распределения напряжений при изгибе балки Э.Мариотта
Следовательно, растягивающие и сжимающие силы в половинах заделанного поперечного сечения равны
N разр p = N разр с = σ разр ba 4 .
Однако при подсчете разрушающей силы Э.Мариотт умножил на плечо a не величину указанных сил, а удвоенную величину, соответствующую эпюре распределения напряжений в первом варианте решения, в результате чего по-прежнему пришел к полученному им ранее соотношению.
Результат, полученный Мариоттом для разрушающей нагрузки, лучше согласовывался с результатами опытов, поставленных им на деревянных и стеклянных стержнях, чем результат, полученный Галилеем. Заметим, впрочем, что Мариотт производил испытания с балками круглого поперечного сечения, а формула была им выведена для прямоугольного поперечного сечения. Расхождения между теоретическими и экспериментальными данными Мариотт объяснил влиянием продолжительности воздействия нагрузки. Оба они не обратили внимания на существование поперечной силы в сечениях балки, точно, так же, как и на необходимость, согласно принятым ими законам распределения нормальных напряжений (первый вариант у Мариотта), существования нормальной сжимающей силы, распределенной по ширине сечения, в нижних волокнах балки.
Интересно отметить, что и Галилей, и Мариотт полагали, что принятые ими законы распределения напряжений справедливы при разрушении, и ставили задачу определения нагрузок, разрушающих балку.
Правильное решение задачи об изгибе балки прямоугольного поперечного сечения было дано А.Параном в 1713г. В первой работе Паран [458] обратил внимание на то, что результат, полученный Мариоттом, справедлив только для балок прямоугольного поперечного сечения. Следуя Мариотту, т.е.предполагая, что эпюра нормальных напряжений имеет вид треугольника), нейтральная линия проходит через нижнюю точку поперечного сечения), он подсчитал разрушающую нагрузку для балки круглого поперечного сечения. Во второй работе [459] Паран принял второй вариант эпюры Мариотта в виде двух треугольников и получил правильное выражение для моментов сопротивления изгибу. Вероятно, Паран понимал, что этой величиной нельзя пользоваться для подсчета разрушающей силы. Для этой цели он предлагал в случае балки прямоугольного поперечного сечения эпюру из двух неодинаковых треугольников. Он обратил внимание на то, что в поперечном сечении консольной балки, нагруженной на конце силой, возникает поперечная сила, по величине равная приложенной.
Приведение круглого поперечного сечения к прямоугольному с наибольшим моментом сопротивления изгибу по А.Парану
Отметим, что Паран дал решение задачи о том, как получить из круглого бревна прямоугольный брус, имеющий наибольший момент сопротивления изгибу. Это решение представлено на рисунке.
Исследование Парана повторил в 1729г. Г.Бюльфингер в работе, опубликованной в 1735г. [332], а затем и Ш.Кулон в 1773г. [352]. Они, по-видимому, не знали о работах Парана.
Заметим, что в одной из первых своих работ Л.Навье придерживается первого предположения, высказанного еще Мариоттом, о том, что нейтральная линия проходит через нижнюю точку поперечного сечения (при изгибе консольной балки силой, направленной вниз).
В 1820 г. А.Дюло [357], решая задачу изгиба балки в плоскости симметрии с поперечным сечением, имеющим одну ось симметрии, определяет положение нейтральной линии не из равенства растягивающих и сжимающих сил в поперечном сечении, а из равенства их моментов относительно нейтральной линии, что приводит к равенству моментов инерции относительно нейтральной линии растянутой и сжатой частей сечения и справедливо очевидно только для поперечного сечения с двумя осями симметрии. Это же положение было высказано инженером Томасом Тредгольдом (TredgoldТ., 1788 — 1829) в 1821 г. [487]. Только Л.Навье в книге, вышедшей в 1826 г. [447], дал правильное решение задачи об изгибе балки произвольного поперечного сечения.
Заметим, что Л.Навье не определил понятие момента инерции площади поперечного сечения. Оно было введено инженером Н.Перси (PersyN.) [461] в 1834г., который разработал теорию моментов инерции. Он же указал, что решение Л.Навье справедливо при условии, что в плоскости действия изгибающего момента лежит одна из главных осей сечения (прямой изгиб).
В статьях И.Ходкинсона [381, 382], опубликованных в 1824 г. и 1831 г., исследуется изгиб призматических стержней. В основу положена степенная зависимость напряжения от деформации, причем для общности принято, что показатели степени при растяжении и сжатии различны. Вероятно, Ходкинсон первым установил, что для балки из материала, одинаково сопротивляющегося растяжению и сжатию, рациональной формой поперечного сечения является двутавр. Он отмечает, что в случае чугунных балок рациональной формой будет тавр с расположением полки в области растяжения, так как механические свойства чугуна при сжатии выше, чем при растяжении.
Задача чистого изгиба стержня прямоугольного поперечного сечения из материала, не подчиняющегося закону Гука и различно сопротивляющегося растяжению и сжатию, решена Б.Сен-Венаном и изложена в дополнении к курсу Л.Навье [447] в 1863 г., а решение задачи упругопластического (без упрочнения) изгиба стержня прямоугольного поперечного сечения приведено в его мемуарах [254] в 1871 г.
Решения различных задач расчета стержней за пределами пропорциональности при изгибе, кручении, а также совместном растяжении, изгибе и кручении изложены в капитальной монографии польского механика и инженера Михала Жычковского (ZyczkowskiM., 1930) [508].
Решение задачи косого изгиба дано Б.Сен-Венаном в 1843г. [475], а внецентренное продольное растяжение или сжатие стержня (т.е .с овместный чистый косой изгиб и растяжение) рассмотрел в 1859 г. Ж.Бресс [329], который ввел понятие ядра сечения и изучил его свойства. Заметим, впрочем, что частный случай внецентренного продольного нагружения стержня прямоугольного поперечного сечения в плоскости симметрии был рассмотрен еще Т.Юнгом в 1807 г. в упомянутой выше книге [506]. Им же было отмечено наличие сдвигов при поперечном изгибе стержня.
Л.Вика в 1833г. [493] экспериментально показал, что в коротких балках поперечная сила оказывает существенное влияние на прочность. На это обращал внимание еще в 1776 г. Ш.Кулон [352].
Приближенное решение задачи определения касательных напряжений при поперечном изгибе балок было дано Д.И.Журавским в 1855 г. в заметке, являющейся частью его труда [172], написанного в связи с проектированием им в течение 1844—1850 гг. деревянных мостов для железной дороги Москва—Петербург. Совокупность работ, связанных с проектированием мостовых пролетных строений с фермами системы Гау, была представлена в Академию наук и награждена ею премией имени Демидова.
Исследование Д.И.Журавского было вызвано тем, что деревянные балки оказывают слабое сопротивление скалыванию вдоль волокон. Им рассмотрены два случая консольных балок: прямоугольного поперечного сечения, нагруженной силой на конце и подверженной воздействию равномерно распределенной нагрузки. Для них получены значения скалывающей силы в нейтральной плоскости и в сечениях, ей параллельных. В первом случае касательные напряжения в продольных сечениях распределены равномерно, а во втором — неравномерно. Интересно, что Д.И.Журавский не использовал дифференциальной зависимости между поперечной силой и изгибающим моментом, как это принято обычно при выводе формулы для касательного напряжения. Эта зависимость, которая представляет собой одно из уравнений равновесия элемента балки, была, по-видимому, установлена инженером И.Шведлером (SchwedlerJ.W.) в 1851г. в работе, посвященной расчету ферм [478]
Для сплошных сечений решение Журавского основано на предположении, что компонент касательного напряжения, параллельный поперечной силе, не изменяется по ширине сечения и позволяет определить только этот компонент. Если поперечное сечение состоит из полос постоянной толщины, изменением касательного напряжения по толщине стенки можно пренебречь, и формула Журавского дает возможность определить полное касательное напряжение. Использование ее для таких сечений позволяет определить положение центра изгиба. Если в плоскости действия внешней нагрузки не лежит центр изгиба, стержень не только изгибается, но и закручивается.
Изучение изгиба и кручения тонкостенных стержней в связи с исследованием устойчивости плоской формы изгиба двутавровой балки было проведено С.П.Тимошенко в 1905—1906гг. [274].
Общая теория изгиба и кручения тонкостенных стержней создана В.З.Власовым и изложена им в ряде работ, обобщенных в монографии [143], первое издание которой вышло в 1940 г., а второе в 1959 г. Первое издание было удостоено Государственной премии в 1941 г.
Решение задач чистого и поперечного изгиба стержня методами теории упругости дано Б.Сен-Венаном в 1856 г. Он показал [255], что при чистом изгибе стержня поперечные сечения его остаются плоскими, а продольные волокна балки не взаимодействуют друг с другом, т.е.напряженное состояние всех точек стержня одноосное. Сен-Венан исследовал изменение формы поперечного сечения при изгибе и установил, что в случае изгиба консоли, нагруженной силой на свободном конце, депланация всех поперечных сечений одинакова, что не вызывает изменения длины волокон и поэтому не оказывает влияния на величины нормальных напряжений, вычисленных на основе предположения о том, что поперечные сечения остаются плоскими. Для этой же задачи Сен-Венан [255] указал на такое распределение касательных напряжений для различных поперечных сечений, при котором удовлетворяются все уравнения теории упругости. Сопоставление результатов точного (Сен-Венана) и приближенного (Журавского) решений для прямоугольного поперечного сечения показывает хорошее согласование их. Заметим, что Сен-Венан высоко оценил исследование Д.И.Журавского.
Таким образом, Сен-Венаном методами теории упругости были решены две важнейшие задачи механики: кручение стержня некруглого поперечного сечения и изгиб стержня. В книге А.Клебша [344] рассмотрен более общий случай нагружения призматического стержня произвольной системой сил, приложенных на торцах. Решение задачи о растяжении и изгибе однородных и неоднородных стержней при помощи теории функций комплексного переменного дано в работе Н.И.Мусхелишвили. Они изложены в упомянутой выше его монографии [213], первое издание которой вышло в 1933 г.
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Дифференциальные зависимости между элементами изгиба балки
Между интенсивностью распределенной нагрузки, перерезывающей силой и изгибающим моментом существуют дифференциальные зависимости, установленные русским ученым Д.И. Журавским и немецким исследователем М. Шведлером.
| Рисунок 8.17 – К определению дифференциальных зависимостей между элементами изгиба |
Рассмотрим балку, загруженную произвольно распределенной нагрузкой q(х), которая описывается одной аналитической зависимостью (рис. 8.17, а). В сечении х выделим двумя параллельными сечениями бесконечно малый элемент dx (рис. 8.17, б). На него действуют: распределенная нагрузка интенсивностью q, которую на бесконечно малой длине элемента dx можно считать постоянной; перерезывающая сила 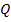
Воспользуемся условие статики для элемента балки dx:
т.е. производная по перерезывающей силе 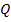
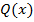
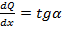
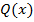
2. 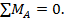
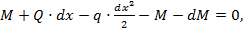
т.е. производная от изгибающего момента в сечении равна перерезывающей силе в том же сечении. Аналогично вышеуказанному, тангенс угла наклона касательной к криволинейной функции М(х) к горизонтальной оси соответствует производной
Подставляя (8.9) в (8.8) получаем:
т.е. вторая производная от изгибающего момента в сечении равна интенсивности распределенной нагрузки в том же сечении.
Зависимости (8.9) и (8.10) составляют суть теоремы Журавского-Шведлера: первая производная от изгибающего момента равна перерезывающей силе в сечении балки, а вторая производная – интенсивности распределенной нагрузки в том же сечении.
Дифференциальные зависимости между элементами изгиба (8.8)-(8.10) используются при согласовании между собой эпюр 
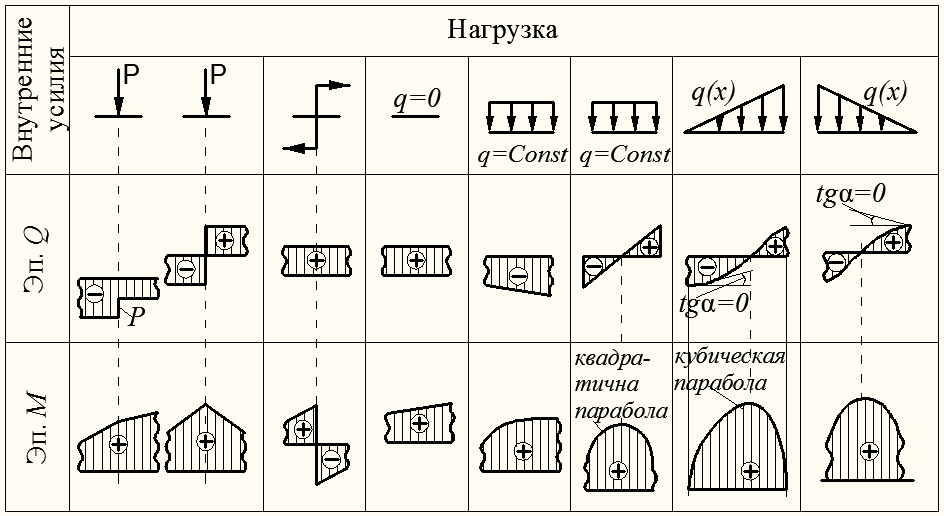
1. На участках балки, на которых перерезывающая сила положительна, изгибающий момент возрастает (слева направо), а на участках, на которых она отрицательна, убывает.
2. Чем больше по абсолютной величине значение перерезывающей силы 
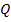
3. На участке балки, на котором перерезывающая сила 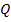
4. Если на границе соседних участков балки эпюра 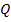
5. Если на границе соседних участков балки на эпюре 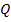
6. Изгибающий момент достигает максимума или минимума в сечениях балки, в которых перерезывающая сила равна нулю; касательная к линии, ограничивающая эпюру М, в этом сечении параллельна оси эпюры.
7. На участках действия распределенной нагрузки q перерезывающие силы изменяются по длине балки (при этом, если интенсивность q постоянна, то перерезывающая сила изменяется по линейному закону); эпюра изгибающих моментов на этих участках ограничены кривыми.
8. На участках балки, на которых распределенная нагрузка отсутствует, перерезывающие силы постоянны, а изгибающие моменты меняются по линейному закону.
9. На участках, где положительный изгибающий момент возрастает, отрицательная перерезывающая сила тоже возрастает; там, где положительный изгибающий момент убывает, положительная перерезывающая сила возрастает.
10. В местах, где к балке приложена сосредоточенная сила, на эпюре 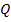
11. Внешний сосредоточенный момент на характере эпюры 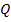
12. Эпюра М всегда обращена выпуклостью навстречу распределенной нагрузке, что следует из формулы (8.10) и совпадения правил знаков для изгибающих моментов и кривизны линии очертания эпюры.
13. Начальные и конечные на эпюрах 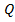
Согласование эпюр 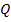
Таблица 8.1 – Согласование эпюр 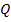
Дата добавления: 2016-10-18 ; просмотров: 4755 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://www.soprotmat.ru/history6.htm
http://poznayka.org/s66536t1.html