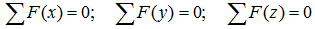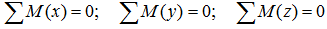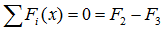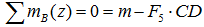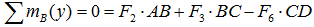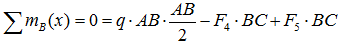Уравнения равновесия узла по моментам

Фермы и их расчёт

Содержание:

Фермой называется шарнирно-стержневая геометрически неизменяемая конструкция.

Плоская ферма – частный случай пространственной конструкции, у которой один из поперечных размеров либо мал по сравнению с другими размерами, либо не существенен для распределения внутренних усилий.

Реальная ферма, может не иметь идеальных шарнирных соединений в узлах, соединения стержней между собой в узлах являются жесткими, а не шарнирными, с помощью сварки, заклепок, болтов или других скреплений.

Плоские фермы конструируют таким образом, что приложенная к ферме нагрузка передается в узлах, вследствие чего, в сечениях элементов ферм не возникают поперечные силы и изгибающие моменты, стержень работает только на продольные усилия – растяжение или сжатие, и, следовательно, реакции стержней будут направлены вдоль этих стержней.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Ферма и их расчет

Ферма — это жесткая конструкция, которая состоит из прямолинейных стержней, соединенных между собой шарнирами. Место, где стержни соединяются друг с другом, носит название узла фермы. Внешняя нагрузка прикладывается к ферме только в ее узлах. Ферма состоит из идеальных стержней, то есть тонких, однородных, невесомых
стержней, на концах которых шарниры, которые работают на растяжение или на сжатие.
Мы будем рассматривать фермы, в которых оси всех стержней и векторы внешних сил содержатся в одной плоскости, то есть, плоские фермы. Помимо этого, конструктивно ферма состоит из стержней, которые образуют собой треугольники, то есть в конструкции фермы нет лишних стержней. такие фермы являются жесткими и статически определенными. В них число стержней n и число узлов m всегда связано таким соотношением

Расчет фермы сводится к определению ее опорных реакций и усилий в стержнях.

Рассмотрим простую плоскую ферму (рис. 1.26).

Как видно из схемы — это плоская конструкция, которая состоит из 7 стержней, которые соединяются в 5 узлах. В узлах I и V ферма имеет опоры (в I-ом узле — неподвижная шарнирная опора; в V-м — подвижная шарнирная опора), к II и к IV узлу фермы приложены внешние нагрузки в виде сосредоточенных сил и ( = 30 kH; = 10 kH). Линейные и угловые размеры фермы данные на схеме (α = 45º). Оси плоской декартовой системы координат I xy показаны на схеме фермы.

Первый этап расчета фермы — это определение ее опорных реакций. Определяют опорные реакции, рассматривая ферму в целом, как твердое тело с приложенными внешними силами. Тогда, условно освобождая ферму от связей (опор) и заменяя их соответствующими реакциями (в узле I это реакции _I, _I; в узле V — _V), имеем плоскую систему произвольных сил, для которой можно использовать условия равновесия и составить систему уравнений равновесия:

Из первого уравнения системы вычисляем неизвестную реакцию X_I. она равна

Из последнего уравнения вычисляем реакцию R_V:

Далее, из второго уравнения является возможность вычислить последнюю неизвестную
величину Y_I. Она будет равняться

Таким образом, вычислено искомые реакции опор фермы. Теперь необходимо определить неизвестные усилия в стержнях фермы. существует несколько способов определения этих усилий, графические и аналитические. Мы рассмотрим два аналитические методы: метод вырезания узлов и метод сечений (или метод Риттера). Рассмотрим последовательно эти методы.

Метод вырезания узлов

Этот метод заключается в последовательном вырезании (мысленно) узлов фермы,
начиная с узла где совпадают два стержня с неизвестными внутренними усилиями. Таким образом, каждый узел — это плоская система сходящихся сил, для которой можно составить два уравнения равновесия, из которых определяют неизвестные усилия в этих двух стержнях.

При применении этого метода принимается правило, согласно которому реакции
стержней направляются от узлов. Если же при определении реакции стержня произойдет, что она имеет отрицательный знак, то этот стержень сжат и действительное направление его реакции ориентировано к узлу.

Определим данным методом усилия в стержнях фермы, приведенной на рис. 1.26. Вырезаем сначала узел I (рис. 1.27). Кроме реакций _I и _I к нему приложены неизвестные реакции стержней 1 и 2, которые обозначаются и и направление которых, по правилу, от узла. Покажем в этом вырезанном узле I оси координат xIy и угол α. Как видно из схемы, узел и находится в равновесии под действием плоской системы сходящихся сил с двумя неизвестными усилиями: и . Составим для узла и уравнения равновесия,
используя условия равновесия для плоской системы сходящихся сил в виде. Будем иметь

Из второго уравнения определяем усилия S₁. Оно равно

Как видим, стержень 1 сжатый усилиям 35,3 kH. С первого уравнения определим неизвестное усилие S₂

Таким образом, стержень 2 растянутый усилием 15,00 kH.

Далее вырезаем узел ІІ (рис. 1.28). В этом узле сосредоточены внешняя сила и усилия трех стержней , и . Причем неизвестные усилия только в двух стержнях — в 3 () и в 4 (). Также предварительно считаем, что стержни 3 и 4 растянуты, и их усилия и
направлены от узла ІІ. Усилия же в стержне 1 уже определено ранее, при вырезании первого узла, и не только установлено ​​его значение, но и то, что он сжат, поэтому направление его реакции будет к узлу ІІ. Проведем через узел ІІ оси координат xy и покажем угол α.

Составим для узла ІІ уравнения равновесия, также используя условия, аналогичные предыдущим.

Из второго уравнения определяем усилия S₃. Оно будет равняться

Как видим, стержень 3 сжатый усилиям 7,00 kH. Направление реакции S₃ — к узлу ІІ.

Из первого уравнения находим усилия S₄. Оно равно

Таким образом, стержень 4 сжатый усилием 20,00 kH.

Далее вырезаем узел IV (рис. 1.29). Он находится под действием внешней силы и усилий в стержнях 4, 5 и 7. Усилия в стержне 4 определено и его направление — к узлу, а потому неизвестны — только усилия и . Проведем через узел IV оси координат xy и покажем угол α. Направления усилий в стержнях 5 и 7 — от узла IV. Составим для узла IV уравнения равновесия, также используя условия равновесия:

Решаем систему, для чего из второго уравнения выразим усилия S₅ через усилия S₇. Оно будет равняться

Теперь подставим значение S₅ в первое уравнение системы. Будем иметь

Стержень 7 сжатый усилием 7,00 kH. Теперь есть возможность найти усилие S₅. Оно равно

Стержень 5 растянутый усилием 7,00 kH.

Теперь, для окончательного определения усилий в стержнях фермы, что рассматривается, необходимо вырезать узел V. К узлу V приложена реакция , усилия , которое направлено к узлу, и неизвестно усилию , которое направляем от узла. Составим для узла V уравнения равновесия, используя условия равновесия:

Как видим, для определения последнего неизвестного усилия S₆ достаточно решить первое уравнение системы. Найдем S₆ :

Стержень 6 растянутый усилием 5,00 kH.

Данные расчетов заносим в таблицу 1.1. Знак при определенном усилии в стержне показывает характер его нагрузки. Если он положительный («+»), То стержень растянут, если отрицательный («–»), то стержень сжат.

Метод Риттера

Рассмотрим второй аналитический метод определения усилий в стержнях плоской фермы. Это метод Риттера, или метод сечений.

Данный метод имеет несколько преимуществ по сравнению с рассмотренным ранее
методом вырезания узлов. Здесь нет необходимости составлять большое количество уравнений равновесия узлов, особенно когда ферма многостержневая. Кроме того, в случае неточности расчета какого-то стержня, в дальнейшем эта ошибка накапливается при расчетах других стержней. Метод Риттера лишен этих неудобств.

Особенность применения этого метода состоит в том, что условно делается сечение всей фермы, при этом в сечении должно быть не больше, чем три стержня с неизвестными усилиями. Тогда рассматривается равновесие одной из частей фермы, а вторая часть отбрасывается. Действие стержней, которые попали в сечение, заменяем их реакциями. предварительно считается, что эти стержни также растянуты, то есть их усилия направлены от узлов. Опорные реакции фермы определяются так же, как и при
применении метода вырезания узлов.

Определим усилия в 4, 5 и 6 стержнях фермы, сделав сечение и рассматривая равновесие правой части фермы (рис. 1.31). Вместо указанных стержней прикладываем в узле IV усилия и а в узле V — усилие . Направления указанных усилий — от узлов. К данной части фермы приложена внешняя сила и реакция . Покажем оси прямоугольной декартовой системы координат Vxy и угол α. Как видим, данная часть
фермы находится в равновесии под действием плоской системы произвольных сил, а
для этого составим для нее уравнения равновесия, используя условия равновесия. Согласно методу Риттера надо составлять уравнения равновесия, как суммы моментов сил относительно тех точек, где пересекаются линии действия большего количества неизвестных усилий. В данном случае такими точками будут точки ІІІ и IV. В отношении этих точек возьмем моменты сил.

Вычислим неизвестные усилия. Из первого уравнения — усилия S₅:

Из второго уравнения — усилия S₄. Оно будет равняться

Таким образом, стержень 4 сжатый усилиям 20,00 kH, направление усилия S₄ будет противоположный тому, который был показан на рис. 1.31.

Расчет плоских ферм

Фермой называется конструкция, состоящая из стержней, соединённых между собой на концах шарнирами и образующих геометрически неизменяемую систему. Шарнирные соединения стержней фермы называют её узлами. Если оси всех стержней фермы лежат в одной плоскости, то ферма называется плоской.

Основные понятия о плоских фермах

Фермой называется геометрически неизменная конструкция, состоящая из прямолинейных стержней, соединенных в узлах шарнирами (рис. 8.1).

Основная задача, о которой будет идти речь далее, заключается в определении внутренних усилий, возникающих в стержнях фермы под действием внешних активных сил.

Приведенное определение фермы имеет одно существенное упрощение, которое позволяет усилия в стержнях фермы находить методами теоретической механики. Этим упрощением является допущение о шарнирном соединение стержней фермы.

В реальных фермах стержни соединены жестко с помощью электросварки, клепки и тому подобное. Однако, как показывают исследования в строительной механике, сделано допущение о способе соединения стержней фермы позволяет найти приближенное значение усилий с достаточной точностью.

Фермы используются в качестве несущих конструкций в различных сооружениях: в мостах, в перекрытиях зданий, в подъемных кранах, каркасах самолетов тому подобное.

Места соединения стержней фермы называются узлами, а те узлы, которыми ферма опирается на основу — опорными узлами. Стержни, размещены по верхнему контуру фермы, образуют верхний пояс, а по нижнем — нижний пояс (См. Рис. 8.1).

Вертикальные стержни называются стойками, а наклонены — раскосами.

Фермы бывают пространственные и плоские. Если оси всех стержней фермы лежат в одной плоскости, такая ферма называется плоской, если нет — то пространственной. В этом разделе ограничимся рассмотрением только плоских ферм.

Расчет ферм существенно упрощается, если сделать такие допущения:
1) трения в шарнирах отсутствует;
2) заданные силы, действующие на ферму, лежат в плоскости фермы и приложенные в узлах;
3) собственный вес стержней малый по сравнению с заданными силами и ею можно пренебречь.

Если выполнять эти условия, каждый стержень фермы будет работать на растяжение или сжатие и не испытывать деформации изгиба, в чем и есть преимущество фермы как строительной конструкции. Действительно, при условии, что все усилия приложены в узлах фермы и отсутствует трение в шарнирах, каждый стержень будет находиться под действием только двух сил, которые приложены к его концов. Согласно с первой аксиомой статики, при равновесии линия действия этих сил должна проходить через их точки приложения. Итак, силы, приложенные к стержню фермы, будут обязательно направлены вдоль стержня, и поэтому приводить его сжатие или растяжение.

Сделанные допущения оправданы тем, что, во-первых, трения в шарнирах малое по сравнению с заданными силами и им можно пренебречь; во-вторых, если сила приложена не у узле фермы, то ее можно разложить на составляющие, которые будут приложены в узлах.

Для того чтобы ферму можно было использовать как несущую конструкцию в инженерных сооружениях, необходимо обеспечить ее жесткость.

Определим условия, при которых ферма будет жесткой (геометрически неизменной).

Условие жесткости фермы

Найдем наименьшее число стержней N, необходимых для построения геометрически неизменяемой (жесткой) фермы, которая имеет n узлов.

Простой, геометрически неизменной фермой является конструкция, состоит из трех узлов, соединенных тремя стержнями. для жесткого присоединения каждого из последующих узлов необходимо два стержня (Рис. 8.2). Полученная таким образом новая конструкция также будет геометрически неизменной фермой.

Следовательно, для обеспечения жесткости фермы (т.е. исключения относительных
перемещений стержней) необходимо, чтобы число стержней равнялось

то есть

Пример неизменной жесткой фермы показано на рис. 8.3, а.

Если число стержней то конструкция будет геометрически переменной (рис. 8.3, б), а если то ферма будет содержать лишние стержни (рис. 8.3, в).

Уравнение (8.1) называется условием жесткости фермы. Заметим, что равенство (8.1) является необходимым условием жесткости фермы, но не достаточным. Для конструкции, изображенной на рис. 8.3, г, условие (8.1) выполняется, но эта система геометрически переменная. Для обеспечения геометрической неизменности фермы условие (8.1) должно выполняться как для всей фермы, так и для отдельных ее частей (решеток).

Статически определенные фермы

Статическую определенность фермы устанавливают по количеству реакций опор и числом стержней фермы.

Заметим, что ферма является неизменной системой, поэтому, как известно из предыдущего, неизвестных опорных реакций не должно быть более трех. В противном случае задача определения опорных реакций для данной фермы является статически неопределенной.

Рассчитывая фермы, кроме трех неизвестных реакций, нужно еще определить усилия в стержнях фермы. Выясним, сколько независимых уравнений статики можно составить для определения этих неизвестных сил. для этого используем метод вырезания узлов.

На каждый вырезанный узел фермы будет действовать плоская система сходящихся сил, которая состоит из внешних сил (активных и реакций связей) и внутренних усилий в стержнях. Поэтому система сил, приложенная к узлу, должна удовлетворять двум уравнениям равновесия

Следовательно, при равновесии фермы, которая имеет n узлов, все действующие на ферму
внешние силы и усилия в стержнях должны удовлетворять 2n уравнением.

С равновесия отдельных узлов фермы следует равновесие фермы в целом, а потому три уравнения равновесия записанные для всей фермы, будут линейными комбинациями первых уравнений, которые являются независимыми.

К 2n уравнениям будут входить три неизвестные реакции связей и внутренние усилия в стержнях. Из этих уравнений можно найти — неизвестных внутренних усилий в стержнях. Если число стержней фермы эти усилия могут быть определены из уравнений статики, и такая ферма называется статически определенной; если усилия в стержнях с помощью одних лишь уравнений статики абсолютно твердого тела определить невозможно и ферма будет статически неопределенной. Заметим, что условие жесткости фермы (8.1) действительно для плоской фермы и является условием статической определенности.

Методы нахождения усилий в стержнях статически неопределенных ферм рассматриваются в курсах сопротивления материалов и строительной механики. В курсе
теоретической механики рассматривают только статически определенные фермы.

Существует три основных метода нахождения усилий в стержнях статически определенных ферм: вырезания узлов Риттера и графический (построения
диаграммы Максвелла-Кремоны).
Остановимся только на двух аналитических методах.

Метод вырезания узлов

Суть метода вырезания узлов заключается в том, что рассматриваем равновесие каждого узла в отдельности. Для этого вырезаем узлы фермы, прикладываем к ним соответствующие внешние силы и реакции стержней и составляем уравнение
равновесия сил, приложенных к каждому узлу. Поскольку в начале расчета фермы неизвестно, какие стержни фермы растянуты, а какие сжаты, условно допускаем, что все стержни растянуты. В этом случае реакции стержней направляем от узлов. Если в результате вычислений получим значение реакций некоторых стержней со знаком минус, то это будет означать, что эти стержни сжаты. Найденные реакции стержней по модулю равны внутренним усилием в стержнях.

Последовательность рассмотрения узлов определяется по условию: число неизвестных сил, приложенных к узлу, не должно превышать количества уравнений равновесия сил, то есть двух.

Проиллюстрируем этот метод на конкретном примере.

Задача 1. Найти усилия в стержнях фермы, изображенной на рис. 8.4, методом вырезания узлов, если к узлу D фермы приложено вертикальную силу

Решение. В этой ферме число узлов n = 8, а число стержней N = 13. Итак, условие (8.1) выполняется и ферма является жесткой без лишних стержней, то есть статически определенной.

Составим уравнения равновесия для всей фермы и найдем реакции опор А и В:

Переходим к определению усилий в стержнях. Условно вырежем все узлы фермы, сохраняя последовательность, указанную выше. реакции стержней обозначим через (рис. 8.5). На основе закона равенства действия и противодействия

Для сил, которые совпадают в каждом узле, составим последовательно уравнения равновесия. Расчет начнем с узла А, в котором приложены только две неизвестные силы и

Равновесие последнего узла В можно не рассматривать, поскольку все усилия найдены. Если правильно найдены все усилия, то условия равновесия узла В будут выполняться тождественно.

Полученные усилия в стержнях 1, 4, 8 и 12 отрицательные, и это означает, что стержни сжаты.

Усилия в отдельных стержнях загруженной фермы, как видно из приведенного примера, могут равняться нулю. Такие стержни принято называть нулевыми.

Сформулируем леммы, которые позволяют найти нулевые стержни плоской фермы, не проводя ее расчета.

Лемма 1. Если в незагруженном узле плоской фермы сходятся два стержни, то усилия в этих стержнях равны нулю.
Лемма 2. Если в незагруженном узле плоской фермы сходятся три стержни, два из которых расположены на одной прямой, то усилия в третьем стержни равна нулю. Усилия в первых двух стержнях равны между собой.
Лемма 3. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилия в этом стержни равна по модулю приложенной силе, а усилия во втором стержне равна нулю.

Довести эти леммы предлагается самостоятельно.

Методом вырезания узлов выгодно пользоваться тогда, когда нужно найти усилия во всех стержнях фермы. Этот метод хоть и простой, но громоздкий и нерациональный в тех случаях, когда нужно найти усилия не во всех стержнях фермы, а только в отдельных. Например, для нахождения усилий только в одном стержне приходится рассматривать
последовательно равновесие определенного количества узлов, пока не будет найдено усилия в нужном стержни. Этот недостаток отсутствует в методе Риттера.

Метод Риттера

Метод Риттера состоит в том, что после нахождения реакций опор ферму условно разрезают на две части так, чтобы в сечении было не более трех стержней с неизвестными усилиями, и рассматривают равновесие одной из частей фермы. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, то есть считают, что стержни розтянути (как в методе вырезания узлов).

На часть фермы, которую рассматриваем в равновесии, будут действовать внешние силы и реакции разрезанных стержней. Для полученной плоской системы сил составляем три уравнения равновесия.

Уравнение выгодно записывать в виде равенства нулю суммы моментов всех сил относительно трех разных центров,которые являются точками, в которых попарно пересекаются разрезанные стержни или их продолжение. Эти точки носят название точек Риттера. В каждое из уравнений моментов относительно трех точек Риттера будет входить лишь одно неизвестное, а именно усилия в том стержни, ось которого через эту точку не проходит. Покажем это на примере.

Задача 2. Методом Риттера найти усилия в стержнях 4, 5 и 6 фермы, изображенной на рис. 8.4.

Решение.Реакции опор фермы найдены в предыдущем примере Условным сечением разделим ферму на две части по стержнях 4, 5, 6 (рис. 8.4) и рассмотрим равновесие левой от сечения части фермы.

Действие правой части на левую заменяем реакциями и(Рис. 8.6).

Для плоской системы сил, которая действует на левую часть фермы, составляем три уравнения равновесия:

где и — точки Риттера, которые показаны на рис. 8.6.

Индексация точек Риттера выбрана так, что уравнение моментов, записанное относительно каждой точки , содержит только одно неизвестное усилиев стержне под номером

Решая эту систему уравнений, получим:

Величины найденных усилий совпадают с полученными ранее методом вырезания узлов.

Аналогично можно найти усилия и в других стержнях фермы. Из приведенного примера видно, что уравнение равновесия не связаны между собой, а потому для нахождения усилий в одном стержне достаточно составить лишь одно из этих уравнений.

Фермы. Способы определения усилий в стержнях ферм

Основными способами определения усилий в стержнях ферм являются: — способ вырезания узлов; — способ сечений Риттера; — графический способ определения усилий в стержнях фермы с помощью построения диаграммы Максвелла-Кремоны; — метод построения веревочного многоугольника.

Простейшие фермы

Фермами называются конструкции, которые состоят из прямолинейных стержней, которые соединены между собой шарнирами и образуют неизменную геометрическую фигуру (рис. 4.1). При расчете ферм весом стержней пренебрегают и считают, что шарниры размещены только на концах стержней; нагрузки, действующие на ферму, приложенные в шарнирах (т.е. в узлах фермы). В этом случае каждый стержень фермы испытывает усилия, действующие вдоль оси стержня, то есть будет растянут или сжат.

С всего класса геометрически неизменных ферм без лишних стержней выделим простые фермы. Их построение происходит так: рассматривается основной треугольник, к нему двумя стержнями присоединяется новый шарнир (узел) и и. д. В дальнейшем будем изучать простые, плоские фермы, где их стержни расположены в одной плоскости.
По своему назначению зачастую фермы делятся на мостовые, стропильные и крановые (рис. 4.1). Установим зависимость между количеством стержней и количеством шарниров (узлов) в простых фермах.
Рассуждаем так: для образования основного треугольника нужно три стержня и три шарнира. Для образования каждого из остальных шарниров (узлов) необходимо два стержня для постоянного соединения с основой фермы. Итак, общее количество стержней в простой ферме с учетом трех стержней основного треугольника определяется так:

(4.1)

Основной задачей расчета простых ферм является определение усилий в стержнях фермы, которые являются внутренними силами, возникающими в стержнях под действием внешних сил. Эту задачу можно решить методами теоретической механики.

Определение усилий в стержнях фермы

Ограничимся двумя способами определения усилий в стержнях простой фермы: способом
вырезания узлов (графически-аналитический метод) и способом Риттера (аналитический метод).

Способ вырезания узлов

Этот способ заключается в том, что каждый узел вырезается из
фермы и рассматривается отдельно как таковой, что находится в равновесии под действием приложенных к нему внешних сил и усилий разрезанных стержней. Система сил, действующей на узел, является плоской системой сходящихся сил, которая находится в равновесии; следовательно, силовой многоугольник, построенный из этих сил, должен быть замкнутым. Построение силовых многоугольников (треугольников) следует начинать с узла, в которых сходятся два стержня, тогда построением замкнутого треугольника (третья сторона отвечает известной заданной силе, прилагаемой в узле) найдутся усилия в этих двух стержнях. После этого можно переходить к следующему узлу и т. Д. Каждый следующий узел выбирается так, чтобы в нем сходилось не более двух стержней с неизвестными усилиями. Так графически будут определены усилия во всех стержнях. Если усилия разрезанных стержней направлены по стержнях в сторону узла, то они сжимающие, в противном случае — растяжимые.
Формально условия равновесия узлов фермы включают в себя условия равновесия фермы в целом, то есть позволяют найти и внешние реакции. Более того, предварительное определение внешних реакций фермы существенно упрощает решения задачи. Рассмотрим способ вырезания узлов на примере расчета усилий в стержнях фермы, показанной на рис. 4.2.

Пример 1. В узле В фермы приложена сила Опорами фермы будут шарнир А и каток С. Определить: реакции опор , усилия стержней в узлах А и D.
Решение. Рассмотрим ферму как твердое тело, которое находится в равновесии под действием плоской системы параллельных сил (в этом случае реакция шарнира будет параллельная силам и , иначе система сил , а следовательно, сама ферма не была бы в равновесии). Проведем ось параллельно силам системы и составим условия равновесия в виде (3.21)

откуда найдем

Определение усилий в стержнях начнем с рассмотрения узла А, в котором сходятся два стержня: 1 и 7. Строим замкнутый треугольник из сил , (рис. 4.2). Для этого в соответствующем масштабе строим вектор, равный вектору реакции , с конца которого проводим прямую, параллельную стержню АВ, а с начала — прямую, параллельную стержню AD. С построенного треугольника находим усилия и . Изображая эти усилия в узле А, видим, что направлено к узлу А по стержню АВ, следовательно, оно — тяговое, а усилия S7 направлено от узла А по стержню AВ, то есть оно — растяжимое. Растяжимое усилия обозначается знаком плюс, а сжимающее — знаком минус. Теперь рассмотрим равновесие сил в узле , в котором остаются только две неизвестные силы: и . Реакция стержня 7, который выходящий из узла равна и противоположная по направлению его же реакции, но приложена в узле А. Опять строим замкнутый треугольник сил: откладываем силу , с ее конца проводим прямую, параллельную стержню 2, сначала — прямую, параллельную стержню 6, и определяем величины и направления усилий и . Аналогично можно определить другие усилия:

Неудобство этого способа заключается в его громоздкости, поскольку приходится строить столько многоугольников, сколько узлов в ферме. Объединение разных многоугольников сил в одну диаграмму осуществили независимо друг от друга английский физик Максвелл и итальянский геометр Кремона, в честь которых эту диаграмму назван диаграммой Максвелла — Кремоны.

Способ Риттера

Этот способ позволяет найти усилия в любом стержни фермы независимо от усилий в других стержнях. Однако предварительно необходимо определить реакции опор фермы.
Способ Риттера состоит в том, что ферма рассекается на две части так, чтобы в сечении было не более трех стержней с неизвестными усилиями, которые не сходятся в одном узле. Отвергая отсеченную часть фермы и рассматривая равновесие той части, оставшейся под действием приложенных внешних сил и усилий, которые заменяют действие рассеченных стержней, получим для этой части фермы три уравнения равновесия с тремя неизвестными усилиями. Чаще всего эти уравнения являются условиями равенства нулю алгебраических сумм моментов сил относительно трех разных центров моментов, за которые выбирают точки парного пересечения рассеченных стержней с числа перерезанных. Эти точки называются точками Риттера.
Если два стержня из трех рассеченных параллельны, то одна точка Риттера удаляется в бесконечность. Тогда составляют два уравнение моментов сил и одно уравнение проекций сил на ось, перпендикулярную к параллельным стержням.

Пример 2. Определить усилия в стержнях 1, 2, 3 фермы, если а другие размеры показано на рис. 4.3.
Решение. Найдем реакции в опорах фермы и . Реакция катка В направлена ​​по нормали к опорной плоскости, а поскольку на ферму действует система параллельных сил то и реакция шарнира А будет параллельной этим:

Отсюда находим Проведем сечение через стержни 1,2,3 и рассмотрим равновесие той части рассеченной фермы, в которой приложено меньшее количество сил. В рассматриваемом случае — это правая часть фермы. Усилия в рассеченных стержнях условно считаем растяжимыми и направлением в сторону части, отбрасываются. Итак, в отсеченной части фермы уравновешивается плоская система сил

Для определения усилия соответствующей точкой Риттера будет точка К, а уравнение равновесия примет вид:

Для определения усилия точкой Риттера является точка В, для определения усилия — точка D, а соответствующие уравнения равновесия имеют вид:

Подставляя необходимые данные, находим
Итак, усилия — растяжимое, — сжимающее (тяговое) , — нулевое (при заданной нагрузке стержень 2 не работает, но с конструкции его изъять нельзя, поскольку нарушится жесткость конструкции и не выполнится условие (4.1)). В завершение сравним методы Максвелла — Кремоны и Риттера, несмотря на их различие, которое заключается в том, что первый метод относится к графическим, а второй — к аналитическим. Как видно из предыдущего изложения, усилия методом вырезания узлов определяются последовательно, переходя от одного узла к соседнему. Поэтому неизбежно накопление ошибок, связанных с неточностью проведение параллельных прямых. Следует отметить, что накопление этих ошибок можно избежать при решении задачи чисто аналитическим способом, составляя уравнения равновесия для системы сходящихся сил, приложенных в узлах фермы.

Но, с другой стороны, взаимосвязь между построением новых вершин диаграммы Максвелла — Кремоны и положением предыдущих, следует рассматривать как определенное ограничение погрешностей, позволяет избежать грубых
ошибок.
Метод Риттера в отличие от предыдущего не приводит к накоплению ошибок, так как все усилия определяются независимо друг от друга, но одновременно не дает возможности заметить грубые ошибки, которые могут случиться при исчислении.

Очевидно, лучшая методика определения усилий в стержнях фермы заключаться в сочетании методов Максвелла — Кремоны и Риттера. Например, все усилия определяются по методу Максвелла — Кремоны и некоторые из них проверяются методом Риттера.

Услуги по теоретической механике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

iSopromat.ru

Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.

При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат

что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы

из условия отсутствия ее вращения относительно указанных осей.

Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.

Пример составления уравнений равновесия

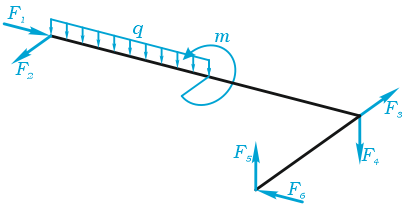
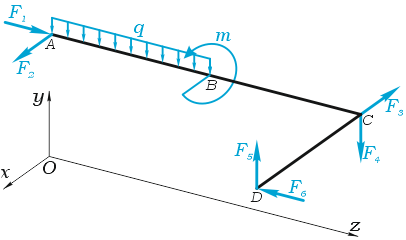
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F₁-F₆, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.

Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.

Суммы проекций сил

Сумма проекций всех сил на ось x (с учетом правила знаков для сил):

здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.

Суммы моментов

Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):

• в плоскости xOy:
  
• в плоскости xOz:
  
• в плоскости yOz:
  

Из полученных шести уравнений можно определить не более шести неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Строительная механика (стр. 6 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12

Для того, чтобы доказать геометрическую неизменяемость фермы, необходимо доказать, что при отсутствии внешней нагрузки в ее стержнях не может возникнуть усилий. Если же оказывается, что при отсутствии нагрузки в стержнях фермы могут существовать ненулевые усилия, то это указывает на равенство определителя матрицы А нулю, а значит и на геометрическую изменяемость фермы.

При выполнении анализа подобного рода, как и при выполнении статического расчета фермы, оказываются полезными правила определения нулевых стержней. Нулевым стержнем называется стержень, в котором при рассматриваемой нагрузке усилие равно нулю. Приведем эти правила.

1. Если в незагруженном узле под углом соединяются два стержня, то оба стержня — нулевые (рис.4.24). В этом легко убедиться, составив уравнения проекций сил на оси, совпадающие с направлением стержней.

2. Если в незагруженном узле сходятся сходятся три стержня, причем два лежат на одной прямой, то третий стержень — нулевой (рис.4.25). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную двум стержням, лежащим на одной прямой.

3. Если к узлу, в котором сходятся два стержня, приложена сила, направление действия которой совпадает с одним из них, то второй стержень — нулевой (рис.4.26). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную линии действия внешней силы.

Рис.4.24 Рис.4.25 Рис.4.26

4. Если в узле сходятся три и более стержней, то те из них, о которых заранее известно, что они являются нулевыми, при определении остальных нулевых стержней и нахождении усилий в стержнях, очевидно, могут быть мысленно отброшены.

5. Если обо всех стержнях кроме одного, сходящихся в незагруженном узле, известно, что они нулевые, то и последний стержень тоже будет нулевым. В этом легко убедиться, составив уравнение проекций сил на ось, совпадающую с направлением этого стержня.

Рассмотрим в качестве примера ферму, изображенную на рис.4.27.

Условие (4.1) выполняется: 22=15×2-8=22. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т. е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отсутствии внешней нагрузки.

Из рассмотрения узлов 5 и 7, согласно признаку 2 нулевых стержней следует, что стержени 3-5 и 7-6 — нулевые. Далее, из рассмотрения узла 3, согласно признакам 4 и 2 следует, что стержень 2-3 нулевой. Далее, из рассмотрения узла 2, согласно признакам 4 и 1 следует, что стержни 1-2 и 2-6 — нулевые. Далее, из рассмотрения узла 6, согласно признакам 4 и 2 следует, что стержень 3-6 нулевой, а значит, в соответствии с признаком 5, нулевым будет и стержень 6-8. Далее, из рассмотрения узла 3, согласно признаку 5 следует, что стержень 1-3 нулевой. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно стержни 8-10, 10-14, 14-15, 9-10, 11-12, 12-14, 10-12 и 12-15 тоже будут нулевыми. Рассмотрим теперь узел 8. В соответствии с признаками 4 и 1 стержень 7-8 будет нулевым. Далее, последовательно рассматривая узлы 7 и 5, пользуясь признаком 5, докажем, что стержни 5-7 и 4-5 — нулевые. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно 8-9, 9-11,11-13, тоже будут нулевыми. Итак, нам удалось доказать, что все стержни фермы при отсутствии нагрузки являются нулевыми. Следовательно, в этом случае в них не может возникнуть ненулевые усилия, а значит ферма геометрически неизменяема.

Теперь рассмотрим ферму, изображенную на рис.4.28.

Условие (4.1) выполняется: 10=7×2-4=10. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т. е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отсутствии внешней нагрузки.

Рассмотрим узел 1. Поскольку на него может действовать только вертикальная опорная реакция, в соответствии с признаком 3 нулевых стержней стержень 1-3 является нулевым. Из рассмотрения узла 7 тот же вывод можно сделать о стержне 5-7. Рассмотрим далее узел 3. На основании признаков 2 и 4 нулевых стержней можно заключить, что стержень 3-5 нулевой.

Рассмотрим далее равновесие опорных узлов. Учитывая отсутствие усилий в стержнях 1-3, 3-5 и 3-7, из рассмотрения равновесия узлов 3 и 5 (из уравнения проекций сил на оси, совпадающие с направлением стержней 2-3 и 6-5) легко заключить, что N2-3 =N3-4 и N6-5 =N4-5. Из уравнения равновесия проекций сил на вертикальную ось для узла 4 (рис.4.31), получим: , где V4-вертикальная опорная реакция.

Рис.4.29 Рис.4.30 Рис.4.31

Легко убедиться, что в каждой их двух других опор действует вертикальная реакция величиной N, направленная вверх. Составим для фермы уравнение проекций всех сил на вертикальную ось. Поскольку внешняя нагрузка отсутствует, в него будут входить только опорные реакции. Очевидно, их равнодействующая равна нулю, а значит система находится в равновесии.

Таким образом, мы доказали, что в стержнях фермы при отсутствии внешней нагрузки может иметься система самоуравновешенных сил, что говорит о том, что ферма геометрически изменяема.

Если бы в процессе подобных рассуждений мы столкнулись с противоречием (например, невозможностью удовлетворить уравнениям равновесия) или доказали бы, что все стержни фермы — нулевые, то отсюда следовала бы невозможность существования такой системы усилий, а значит ферма была бы геометрически неизменяемой.

Статический расчет фермы

Статический расчет фермы заключается в определении реакций в ее опорах и нахождении усилий в ее стержнях.

Для статически определимых ферм для решения данной задачи, как известно, достаточно только уравнений равновесия. Составив для каждого узла по два уравнения равновесия проекций всех сил на вертикальную и горизонтальную оси, получим замкнутую систему уравнений (4.2), решив которую найдем усилия во всех стержнях фермы и реакции опор. Данный алгоритм может быть относительно просто реализован в виде программы для ЭВМ. Кроме того, статический расчет фермы может быть выполнен с применением программных комплексов на основе метода конечных элементов.

В то же время, при расчете ферм с небольшим количеством стержней, а также при проверке результатов расчетов, полученных на ЭВМ, может потребоваться использование простейших приемов определения усилий в стержнях ферм. К ним относятся способ вырезания узлов и способ сечений.

Способ вырезания узлов уже использовался нами при статическом анализе геометрической неизменяемости фермы. Он заключается в мысленном вырезании узла фермы с заменой действия на него стержней соответствующими усилиями. Эти усилия связаны между собой и приложенной к стержню внешней нагрузкой (или опорными реакциями) посредством статических уравнений равновесия. Для любого узла можно составить два таких уравнения — равенства нулю суммы проекций всех сил, например, на вертикальную и горизонтальную оси. Очевидно, если в узле сходятся два стержня (например, рис.4.24 и рис.4.26), то из этих уравнений могут быть найдены усилия в обоих из них. Если узел соединяет три стержня, но усилие в одном из них уже найдено из рассмотрения равновесия другого узла или использованием способа сечений, то из этих двух уравнений могут быть найдены усилия в двух оставшихся стержнях.

Способ сечений состоит в мысленном рассечении фермы на две части и рассмотрении равновесия одной из них. При этом действие отбрасываемой части на рассматриваемую должно быть заменено усилиями в стержнях ферм. Если провести сечение таким образом, чтобы оно проходило через три стержня, то можно составить уравнения равновесия для рассматриваемой части фермы таким образом, чтобы найти усилия во всех трех стержнях.

В качестве примера рассмотрим ферму, изображенную на рис.4.1. Для определения усилия в любом из ее раскосов, а также в любом стержне верхнего или нижнего пояса достаточно провести вертикальное сечение в соответствующей панели фермы и рассмотреть равновесие любой отсеченной части. Очевидно, выгоднее рассматривать равновесие той части, для которой проще составить уравнение равновесия (рис.4.32).

Если составить уравнение равновесия моментов относительно точки А, то в это уравнение войдет только одно неизвестное усилие — усилие NНП в стержне нижнего пояса. Следовательно, это усилие может быть определено из этого уравнения. Если составить уравнение равновесия моментов относительно точки В, то в это уравнение также войдет только одно неизвестное усилие — усилие NВП в стержне верхнего пояса. Следовательно, это усилие может быть определено из этого уравнения. Если составить уравнение равновесия проекций всех сил на вертикальную ось, то в это уравнение войдет только одно неизвестное усилие — усилие в раскосе NР. Следовательно, это усилие может быть определено из этого уравнения. Для определения усилия в стойке сечение нужно выполнять так, чтобы оно проходило через нее (рис.4.33).

Если составить уравнение равновесия проекций всех сил на вертикальную ось, то в это уравнение войдет только одно неизвестное усилие — усилие в стойке NС. Следовательно, это усилие может быть определено из этого уравнения.

Если в сечение попадает количество стержней превышающее три, то чаще всего приходится комбинировать способ сечений и способ вырезания узлов, определяя усилия в части из стержней в сечении из рассмотрения равновесия узлов или при выполнении других сечений.

Таким образом, усилие в любом стержне статически определимой фермы может быть определено в один или несколько шагов путем последовательных вырезаний узлов и/или рассмотрением равновесия отсеченных определенным образом частей фермы.

Очевидно, при использовании этих способов необходимо предварительное определение опорных реакций из уравнений равновесия фермы.

Другие способы определения усилий в фермах

Рассмотренные выше способы определения усилий (способ вырезания узлов и способ сечений) можно отнести к основным способам расчета ферм.

Однако в некоторых случаях ни один из них не приводит к желаемому результату, и тогда приходится прибегать к другим способам расчета. Рассмотрим некоторые из них.

Способ замкнутого сечения

Пусть требуется определить усилия в стержнях фермы Шухова (рис.4.34,а). Применение способа вырезания узлов нецелесообразно, так как здесь нет узлов, в которых сходились бы только два стержня с неизвестными усилиями, и нельзя использовать способ проекций, так как невозможно провести сечение через три стержня.

а) б)

Проведем замкнутое сечение так, чтобы три стержня (1, 4, 7) пересекались по одному разу, а стержни 8, 9, 10 – по два раза. Рассмотрим равновесие отсеченной части фермы внутри замкнутого контура (рис.4.34,б). Усилия в стержнях 8, 9, 10, перерезанных замкнутым сечением дважды, уравновешиваются. А усилия в стержнях 1, 4, 7 можно определить способом моментной точки, после чего легко определить усилия в остальных стержнях фермы.

Способ совместных сечений

Применение этого способа приводит к системе двух уравнений с двумя неизвестными. Способ используется в тех случаях, когда удается провести два сечения таким образом, что каждое из них содержит четыре неизвестных, причем какие-то два неизвестных усилия повторяются в обоих сечениях. Ниже будет рассмотрен пример определения усилий способом совместных сечений.

Графический способ определения усилий

Этот способ основан на графическом приеме разложения силы на два направления и состоит в следующем: буквами или цифрами обозначают полигоны (поля), т. е. площади, ограниченные со всех сторон стержнями или примыкающие к наружному контуру фермы и отделенные друг от друга внешними силами, включая опорные реакции (рис.4.35).

В результате каждое внутреннее усилие и каждая внешняя сила обозначаются двумя значками, соответствующими названиям тех полигонов, границей которых эта внешняя сила или усилие является. Строят многоугольник сил на внешних силах, включая опорные реакции. Каждая из сил этого многоугольника обозначается буквами или цифрами, поставленными на ее концах, при этом сохраняется направление сил.

Затем выбирают узел, в котором сходятся два стержня. Приложенную в узле силу раскладывают по направлениям этих стержней, в результате чего определяют значения и направления действующих в них усилий (направления определяют растяжение–сжатие). Разложить силы на две составляющие можно построением силового треугольника. Такой треугольник должен быть замкнут, так как узел, для которого он строится, находится в равновесии. Если к узлу приложены две и более известных сил, то строят многоугольник равновесия известных и неизвестных сил. После этого переходят к следующему узлу и для него проводят аналогичные построения. Таким образом, определяют усилия во всех стержнях фермы.

Пример расчёта ферм на неподвижную нагрузку

Выполним статический расчет фермы, изображенной на рис.4.36.

Теперь исследуем правильность расстановки связей в ферме. Данная ферма образована двумя жесткими дисками. Контур первого из них ограничен узлами 1,4,6,5,2. Действительно, жесткий диск образован тремя шарнирными треугольниками, к которым двумя стержнями, не лежащими на одной прямой, присоединен узел 5. Второй диск, контур которого ограничен узлами 6,8,7,10,9, также образован тремя шарнирными треугольниками, т. е. представляет собой простейшую ферму. Два диска соединены между собой тремя связями, линии действия которых не параллельны и не пересекаются в одной точке,- в узле 6 и стержнем 5-7. Таким образом, вся конструкция также представляет собой жесткий диск. Он прикреплен к основанию тремя связями, линии действия которых не параллельны и не пересекаются в одной точке. Следовательно, на основе структурного анализа можно сделать вывод, что данная ферма является геометрически неизменяемой.

Определим опорные реакции в ферме. Горизонтальная нагрузка на систему отсутствует, следовательно горизонтальная реакция в левой опоре равна нулю H1 = 0. Поскольку данная ферма симметрична и находится под действием симметричной нагрузки, очевидно, вертикальные реакции V1 и V10 должны быть равными. Найдем их из уравнения проекций всех действующих на систему сил на вертикальную ось: V1+V10 = 3∙20 кН. Следовательно, V1=V10 = 30 кН.

Теперь приступим к определению усилий в стержнях фермы. Прежде всего выделим нулевые стержни. Из рассмотрения узла 5 на основании признака 2 нулевых стержней следует, что стержень 5-6 нулевой.

Мысленно рассечем ферму сечением, изображенным на рис.4.37 и рассмотрим равновесие левой части. Напомним, что положительное значение продольного усилия соответствует растяжению стержня, а отрицательное — сжатию. Поэтому при составлении уравнений равновесия будем считать неизвестные стержневые усилия растягивающими.

Из уравнения моментов относительно точки А: 30кН ∙ 4м — 20кН ∙ 2м + N2-5 ∙ 2м = 0 находим N2-5 = -40кН, а из уравнения моментов относительно точки В (ее положение легко определяется из подобия треугольников А43 и АВС) 30кН ∙ 8м — 20кН ∙ 6м — N3-6 ∙ 2м = 0 находим N3-6 = 60кН.

Усилие N4-6 можно определить из уравнения проекций всех сил на вертикальную ось 30кН — 20кН + N4-6 ∙ sinα = 0.

Усилия в остальных стержнях левой половины фермы можно найти, например вырезанием узлов 2, 3 и 4.

Рассмотрим равновесие узла 2 (рис.4.38). Он соединяет три стержня, но в одном из них усилие уже найдено — усилие в стержне 2-5 является сжимающим и равно 40кН. Следовательно, двух уравнений равновесия этого узла будет достаточно, чтобы определить усилия в двух других стержнях. Из треугольника 123 следует, что β = 450.

Теперь рассмотрим равновесие узла 3 (рис.4.40). Усилия в трех стержнях из четырех, соединяющихся в этом узле, уже известны. Из уравнения проекций всех сил на горизонтальную ось находим N1-3 = 60кН. Запишем уравнение проекций сил на вертикальную ось: 40кН=20кН+20кН. Полученное равенство является истинным, что подтверждает правильность полученных значений усилий в стержнях ферм.

Итак, значения усилий в стержнях левой половины фермы определены. Усилия в стержнях на правой половине фермы находятся исходя из симметрии фермы и симметричности приложенной к ней нагрузки. Значения усилий (кН), определенные в результате расчета, приводятся на рис.4.41.

Проверки правильности определения усилий в стержнях фермы также можно осуществить вырезанием узлов или использованием способа сечений.

Пример расчета фермы на подвижную нагрузку

Рассмотрим ферму, изображенную на рис.4.36. Необходимо:

1. Используя теорию линий влияния, определить усилие в стержне фермы 2-3 от действия неподвижной системы сил, изображенной на рис.4.36.

2. Определить максимальное и минимальное усилия в стержне фермы 2-3 при движении по ездовой линии (по горизонтали от узла 1 к узлу 10) системы из двух сил (рис.4.57).

3. Определить усилие от постоянной равномерно распределенной нагрузки q=10кН/м, приложенной к поясу фермы, совпадающему с ездовой линией (рис.4.58).

Построим линию влияния для стержня фермы 2-3. Для этого достаточно определить усилие в этом стержне при различных положениях единичной силы на ездовой линии.

Cоставим уравнения равновесия узла 2 (рис.4.60):

Согласно этой формуле, при x=0 ордината линии влияния, как и следовало ожидать, равна нулю, а при x=2м она равна 1/2. По этим точкам строится левая ветвь линии влияния (до точки С на рис.4.63).

Таким образом, при x=4м ордината линии влияния равна 1 (точка D на рис.4.63), а на правой опоре, как и следовало ожидать — нулю. По этим точкам строится правая ветвь линии влияния, и далее передаточная прямая CD. В рассматриваемом случае ее направление, как мы видим, совпадает с направлением левой ветви линии влияния, а сама линия влияния оказалась симметричной.

Теперь приступим к определению усилий в стержне 2-3.

Наиневыгоднейшим положением подвижной системы двух сил на ездовой линии (рис.4.57) будет положение, когда одна из них находится ровно посередине пролета фермы (рис.4.64), т. к. в этом случае одна из сил оказывается над единственной в рассматриваемом случае вершиной линии влияния. Ордината линии влияния под силой в центре фермы равна 1, ординату под точкой приложения второй силы легко определить из подобия треугольников: откуда y=0,8 (рис.4.64). В соответствии с (4.3) усилие в стержне составит. В силу симметрии линии влияния, в случае, когда над ее вершиной в центре пролета фермы окажется не левая, а правая сила, результат будет тем же.

Построенная линия влияния не имеет отрицательных ординат, следовательно, при любом положении системы сил на ездовой линии в стержне будут возникать только растягивающие усилия. Поэтому, максимальным возможным усилием в стержне 2-3 для рассматриваемой подвижной нагрузки является 36 кН, минимальным -0 кН.

Наконец, определим усилие в стержне от действия неподвижной равномерно распределенной по всей длине ездовой линии нагрузки (рис.4.58) q=10 кН/м. Площадь фигуры, ограниченной линией влияния (рис.4.63) составляет. Размерность площади фигуры оказалась такой, поскольку единичная сила, а следовательно и ординаты линии влияния продольного усилия не имеют размерности.

Расчет трехшарнирных арок

Общие определения арки

Арка — система криволинейных стержней. К статически определимым системам относятся трехшарнирные арки, имеющие шарнирные опоры на краях и один промежуточный шарнир, чаще всего — центральный (рис.5.1).

Пролет арки — расстояние между ее опорами L. Опору арки принято также называть пятой арки, центральный шарнир — замком арки, а расстояние f от прямой, соединяющей опорные шарниры до замка арки, — стрелой арки или стрелой подъема арки.

Арки относятся к распорным системам, т. е. таким системам, в опорах которых, в отличие от безраспорных систем, при действии только вертикальной нагрузки возникает ненулевое горизонтальное усилие, называемое распором.

Инженер-строитель может столкнуться с необходимостью выбора между безраспорной системой (балкой) и распорной системой (аркой) для выполнения перекрытия некоторого пролета, например, мостового. При этом арку сопоставляют с соответствующей балкой, т. е. простой балкой на двух опорах, перекрывающей такой же пролет и находящейся под действием такой же вертикальной нагрузки, что и арка.

Частным случаем трехшарнирной арки является трехшарнирная арка с затяжкой (рис.5.2).

Затяжка — горизонтальный стержень, предназначенный для полного или частичного восприятия горизонтального распора. Для того, чтобы система при наличии затяжки осталась статически определимой, одну опору арки делают катковой. В этом случае, при отсутствии горизонтальной составляющей нагрузки горизонтальные реакции в опорах будут равными нулю, а затяжка будет воспринимать распор полностью.

При нагрузке определенного вида очертание арки можно задать таким, чтобы в ней не возникало изгибающих моментов. Такие арки называют арками рационального очертания.

Задание геометрии арки

При задании геометрии арки необходимо определить величины пролета L, стрелы f, и функцию y(x), описывающую очертание оси арки (рис.5.1). Для арки с затяжкой, кроме того, необходимо задать высоту над затяжкой f’ (рис.5.2).

Задав значения L и f, мы определяем положение трех точек — опор и замка арки. Если дополнительно потребовать, чтобы ось арки была очерчена по окружности или по параболе, то положение этих трех точек однозначно определит функцию y(x), поскольку через три точки можно провести только одну окружность и только одну параболу.

Угол в (5.1) и (5.2) — угол наклона касательной к оси арки в данной точке (рис.5.1). На левой половине арки, на правой. Справедливость формул (5.1) и (5.2) читателю предлагается проверить самостоятельно.

Понятно, что ось арки может быть очерчена не только по параболе или окружности.

Статический расчет трехшарнирной арки

В принципиальном отношении расчет трехшарнирной арки не отличается от расчета других статически определимых систем: вначале определяются опорные реакции, затем строятся эпюры изгибающего момента, продольного и перерезывающего усилия, после чего выполняются проверки и, при необходимости, определяются перемещения. Единственная особенность, с которой приходится сталкиваться, — появление чисто вычислительных трудностей, связанных с криволинейностью очертания оси арки.

Как в любой статически определимой системе, реакции в опорах трехшарнирной арки находятся исключительно из статических уравнений (уравнений равновесия). Примем положительные направления реакций в опорах арки в соответствии с рис.5.3.

Из условия равенства нулю суммы проекций всех действующих на систему сил на вертикальную ось имеем:

где — сумма проекций всех действующих на арку внешних сил на вертикальную ось. В (5.3) внешняя сила считается положительной, если она направлена вниз.

Далее, составим уравнение моментов всех действующих на систему сил относительно произвольной точки. Здесь в качестве точки, относительно которой будут вычисляться моменты, выберем точку А. Поскольку линии действия трех опорных реакций из четырех проходят через эту точку, в уравнении останется только одна неизвестная реакция — VB.

где — суммарный момент действующих на систему внешних сил относительно точки А. В (5.4) он считается положительным, если направлен по часовой стрелке.

Уравнений (5.3) и (5.4) достаточно, чтобы найти вертикальные реакции в опорах арки. Составив аналогичные уравнения для балки, соответствующей арке (рис.5.3), легко убедиться, что при отсутствии горизонтальной составляющей нагрузки эти уравнения совпадут с (5.3) и (5.4), а значит вертикальные реакции VA и VB в опорах арки и соответствующей ей балки будут одинаковыми.

Четвертое уравнение — условие равенства нулю суммы моментов всех сил, действующих на систему с одной (любой — левой или правой) стороны от промежуточного шарнира относительно этого шарнира.

При отсутствии горизонтальной составляющей внешней нагрузки горизонтальные реакции в опорах арки будут равны и направлены противоположно друг другу, что следует из уравнения (5.5):

Горизонтальное усилие H, возникающее в опорах, называется распором.

Из уравнений (5.3)-(5.6) можно найти четыре неизвестные опорные реакции HA, HB, VA и VB, после чего приступить к определению изгибающих моментов в сечениях арки.

Рассмотрим сечение, находящееся на произвольном расстоянии х от левой опоры арки (рис.5.3). Рассматривая равновесие части арки с одной стороны от данного сечения, найдем в нем изгибающий момент. Будем рассматривать часть арки слева от сечения.

Как мы уже выяснили, при отсутствии горизонтальной составляющей нагрузки вертикальные опорные реакции VA и VB в арке и в соответствующей ей балке будут одинаковыми, а горизонтальные реакции в опорах арки равны и противоположно направлены. Изгибающий момент в балке определяется по формуле. Сопоставляя эту формулу с (5.8), с учетом (5.7) .

Таким образом, при условии отсутствия горизонтальной составляющей нагрузки, зная распор в арке и изгибающий момент в любом сечении балки, соответствующей рассматриваемой арке, момент в этом же сечении арки можно найти и по формуле (5.9).

Для определения продольного и перерезывающего усилий рассмотрим сечение в арке, отстоящее от левой опоры на произвольное расстояние х (рис.5.3).

При определении опорных реакций и распора в арках с затяжкой, затяжку мысленно удаляют, заменяя ее действие на остальную часть конструкции усилиями H (рис.5.7).

Далее составляют обычные уравнения равновесия.

Если далее рассматривать распор в затяжке Н как одну из внешних нагрузок (рис.5.7), то построение эпюр внутренних усилий можно выполнить аналогично арке без затяжки по формулам (5.8), (5.10) и (5.11).

Преимущества и недостатки арок по сравнению с балками

1. Для большинства строительных конструкций, таких как перекрытия зданий, пролетные строения мостов и т. п. основной нагрузкой является вертикальная нагрузка, направленная вниз. Легко убедиться, что для такой нагрузки горизонтальные реакции в опорах арки будут направлены навстречу друг другу, т. е. значение распора Н будет положительным (см. например, “Пример расчета арки параболического очертания под действием вертикальной нагрузки” и “Пример расчета арки с затяжкой”). Основным достоинством арочных конструкций является то, что в этом случае, в соответствии с формулой (5.9) изгибающий момент в любом сечении арки всегда меньше, чем в том же сечении соответствующей балки. За счет этого, а также за счет действующих в арке продольных сжимающих усилий, растягивающие напряжения в сечениях арки малы или отсутствуют (рис.5.23). Это очень важно для каменных и бетонных конструкций, которые, как известно, могут выдерживать высокие сжимающие напряжения, но практически не работают на растяжение.

2. Арочные конструкции отличаются большей эстетичностью.

3. Балочные конструкции значительно более технологичны с точки зрения изготовления, транспортировки и монтажа по сравнению с арочными.

4. Арки передают на опоры значительные горизонтальные усилия (рис.5.24). В связи с этим, опоры арочных конструкций должны быть достаточно мощными, чтобы воспринять эти усилия и передать их на основание.

Использование арок с затяжками позволяет значительно уменьшить горизонтальные опорные реакции. Металлическую затяжку применяют, например, для уменьшения нагрузок на пяту каменного свода (рис.5.25).

Арки рационального очертания

Арка рационального очертания — такая арка, в каждом сечении которой при вертикальной нагрузке определенного вида изгибающий момент равен нулю.

Поскольку f не зависят от координаты x, из (5.17) следует, что y(x) должна быть пропорционально изгибающему моменту в балке, соответствующей рассматриваемой арке.

Итак, для построения арки рационального очертания для нагрузки определенного вида достаточно построить эпюру изгибающего момента в балке, соответствующей данной арке, и, задавшись значением f, определить очертание арки по формуле (5.17). В частности, рациональным очертанием для арки, загруженной равномерно распределенной нагрузкой, будет параболическое очертание, поскольку изгибающий момент в соответствующей балке меняется по закону параболы (рис.5.26). На рис.5.27 и рис.5.28 приведены примеры арок рационального очертания для нагрузок других видов.

Расчет плоских статически определимых рам

Построение эпюр для плоских рам

Плоской рамой называется стержневая система, элементы которой жестко или шарнирно соединены между собой, нагруженная в своей плоскости.

Вертикально (или под наклоном) расположенные стержни рамы называются стойками, а горизонтальные — ригелями. Жесткость узлов устраняет возможность взаимного поворота скрепленных стержней, то есть в узловой точке углы между их осями остаются неизменными.

Как и многие другие системы, рамы делятся на статически определимые и статически неопределимые (рис.6.1, б, в,д, е).

Промежуточный шарнир снижает степень статической неопределимости рамы на величину m — 1, где m — число стержней, сходящихся в шарнире. Если m >2, то шарнир называется кратным (рис.6.1, д).

Для определения степени статической неопределимости плоской рамы можно воспользоваться формулой:

где n — степень статической неопределимости; К — число замкнутых контуров в предположении полного отсутствия шарниров; Ш — число шарниров в пересчете на одиночные.

Основание (земля) рассматривается как стержень.

Для рамы (рис.6.1, б) имеем:

Для рамы (рис.10,д):

В более простых случаях, когда отсутствуют замкнутые контуры и промежуточные шарниры, то есть когда используются комбинации тех же опор, что и в балках (жесткая заделка, шарнирно-подвижная и шарнирно-неподвижная опоры), для определения степени статической неопределимости используется “балочная” формула.

В данной работе ограничимся рассмотрением простейших статически определимых рам трех видов:

1) с жесткой заделкой;

2) на двух шарнирных опорах (неподвижной и подвижной);

3) на двух шарнирно неподвижных опорах с простым промежуточным шарниром.

Для изгибающих моментов специального правила знаков нет, а при вычислении момента в любом сечении знак принимается произвольно. Но результат вычислений всегда откладывается со стороны сжатого волокна элемента рамы. При этом знак на эпюре никогда не указывается. Такое условие полностью соответствует характеру построения эпюр в балках, где в соответствии с принятым для изгибающих моментов правилом знаков (см. 1.7) ординаты эпюр всегда оказывались расположенными со стороны сжатых волокон балки.