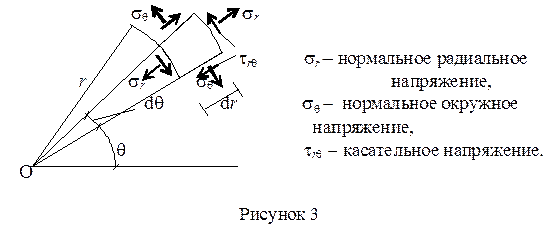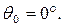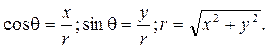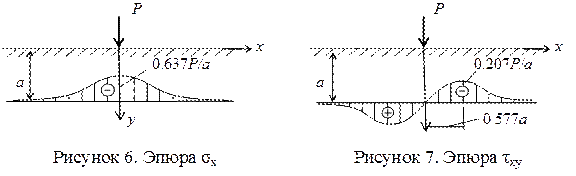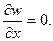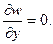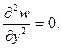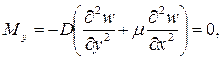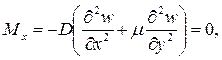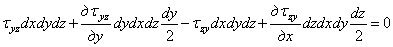Уравнения равновесия в полярных координатах

Плоская задача теории упругости в полярных координатах

При решении плоской задачи в полярных координатах ряд инженерных задач удается решить путем непосредственного интегрирования исходных дифференциальных уравнений. Ориентация и обозначение напряжений в полярной системе координат показаны на рисунке 3.

Основные уравнения плоской задачи теории упругости в полярных координатах имеют вид:

(8)

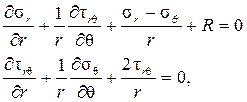
уравнение совместности деформаций в напряжениях:

(9)

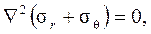
где Ñ 2 — гармонический оператор Лапласа в полярных координатах:

, (10)

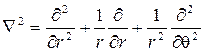
соотношения Эри и бигармоническое уравнение:

(11)

(12)

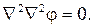
Несмотря на более громоздкий вид уравнений плоской задачи в полярных координатах для ряда инженерных задач удается найти решение в замкнутом виде.

Одной из таких задач является задача о простом радиальном напряженном состоянии, когда при интегрировании уравнений (8) и (9) получают следующее напряженное состояние:

; . (13)

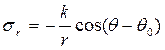
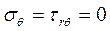
Этому состоянию соответствует задача о клине, нагруженном силой в вершине (рисунок 4).

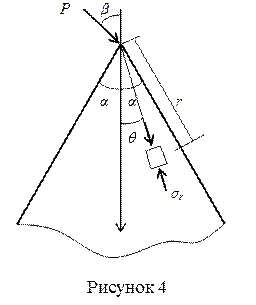Значения постоянных k и q₀, можно вычислить, воспользовавшись следующими формулами:

(14)

; (15)

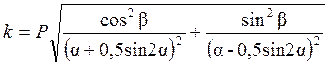
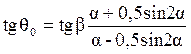
где a — угол полураствора клина и b — угол отклонения силы Р от биссектрисы угла.

Большое инженерное решение имеет частный случай — задача Фламана о действии силы на полуплоскость (рисунок 5).

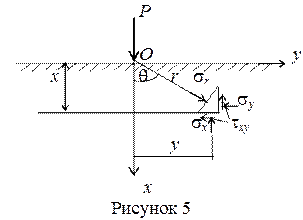В этом случае угол полураствора клина равен a = 90°, угол b = 0°.

Постоянные: k =

Выражение для напряжений принимает вид:

Рассмотрим напряженное состояние полуплоскости на разных глубинах. Для этого удобнее перейти к декартовым координатам.

Воспользуемся выражениями для напряжений по наклонным площадкам:

(16)

(17)

(18)

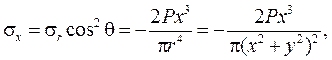
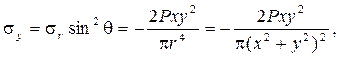
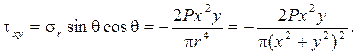
На рисунках 6 – 8 показаны эпюры напряжений в слое, отстоящем от поверхности полуплоскости на расстоянии а.

Изгиб прямоугольной пластинки

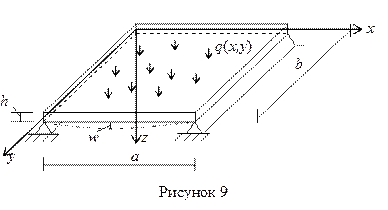
При решении задач изгиба прямоугольной пластинки (рисунок 9) функцию прогиба w(x,y) находят путем интегрирования бигармонического уравнения изгиба пластинки:

(19)

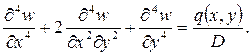
Как было указано во введении, основная и наиболее трудоемкая часть задачи расчета жесткой пластинки заключается в определении функции w(x,y) как решения бигармонического уравнения Софии Жермен — Лагранжа (19), удовлетворяющего заданной нагрузке и условиям опирания пластинки. Здесь q(x,y) –поверхностная нагрузка на пластинку; – цилиндрическая жесткость пластинки; h – толщина пластинки.

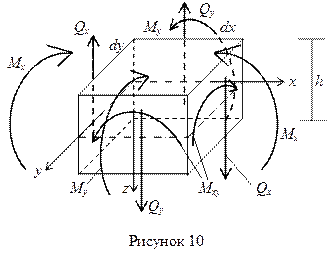
Внутренние усилия (рисунок 10) и напряжения в пластинке связаны с перемещениями следующими зависимостями.

(20)

(21)

(22)

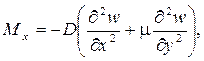
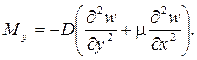
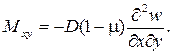
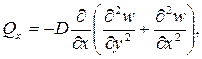
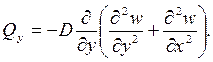
Согласно принятой в теории изгиба пластинок гипотезы Бернулли – Кирхгофа о жесткой нормали, напряжения, создающие изгибающие моменты M_x, M_y, определяются по формулам сопротивления материалов:

, (23)

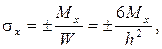
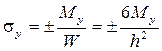
где W = 1·h 2 /6 – момент сопротивления элемента поперечного сечения пластинки единичной ширины.

Таким образом, если известна функция w(x,y), то, вычислив максимальный прогиб, можно проверить условие жесткости. Далее, определив внутренние усилия по выражениям (20) и (21), можно найти их максимальные значения и по формулам (23) вычислить наибольшие напряжения и дать оценку прочности пластинки.

Уравнение (19) имеет множество решений и для отыскания своего решения необходимо воспользоваться граничными условиями – условиями опирания пластинки.

Запись условий опирания.

В теории пластинок приняты три основных вида опирания – защемление, свободное (шарнирное) опирание и свободный неопертый край.

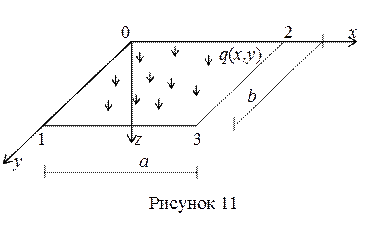
Пусть левый край пластинки 0-1 с координатами х = 0, 0 ≤ у ≤ b защемлен (рисунок 11). В этом случае граничные условия принимают вид:

2) угол поворота левой грани

Если защемлены верхний или нижний края пластинки, условия опирания имеют аналогичные выражения:

1) прогиб w = 0, 2) угол поворота нижней (верхней) грани

Верхний край 0 — 2 с координатами 0 ≤ x ≤ a, y = 0 шарнирно оперт. Тогда граничные условия записываются как:

Изгибающий момент на грани M_y = 0. Поскольку производная по х на верхней опертой грани 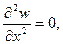второе условие принимает вид:

2) M_y =

Если шарнирно оперты боковые грани, то условия опирания имеют вид:

1) w = 0, 2) M_x =

Пусть нижний край 1-3 (0 ≤ x ≤ a, y = b ) неоперт. В этом случае w ≠ 0, а нулю должны быть равны усилия (реакции) на свободном неопертом крае. Т. е.

Два последних условия можно объединить в одно 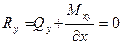и граничные условия примут вид:

1)

2) .

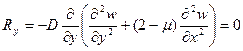
Если неоперты правый или левый край, то граничные условия запишутся как:

1)

2) .

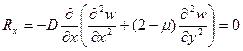
Плоская задача теории упругости в полярных координатах

Автор: Леонид Савенков • Март 24, 2020 • Реферат • 2,290 Слов (10 Страниц) • 211 Просмотры

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ) ИМЕНИ И. М. ГУБКИНА»

Кафедра технической механики

по дисциплине: «Основы теории упругости, теории пластичности и механики разрушения»

на тему «Плоская задача теории упругости в полярных координатах»

1. Введение…………………………………………………………………. 3
2. Общие уравнения равновесия в полярных координатах……………………..………………………………………….4
3. Основные уравнения равновесия…………………………………………5
4. Геометрические уравнения ……………………………………………….8
5. Физические уравнения…………………………………………………. 10
6. Статические уравнения…………………………………………………. 11
7. Соотношения, связанные с функцией напряжений……………………..13
8. Заключение……………………………………………………………….. 15
9. Список используемой литературы……………………………………….16

Плоская задача теории упругости в полярных координатах.

Теория упругости – раздел механики сплошных сред, изучающий деформации упругих твёрдых тел, их поведение при статических и динамических нагрузках. Главная задача теории упругости – выяснить, каковы будут деформации тела и как они будут меняться со временем при заданных внешних воздействиях. [1]

Цель моего реферата — изучить плоскую задачу теории упругости в полярных координатах, вывести основные уравнения, закон Гука в полярных координатах, а также выяснить, когда задачу теории упругости удобнее решать в полярных координатах. Данная тема является актуальной и по сей день, поскольку ряд задач теории упругости удобно решать не в прямоугольных, декартовых координатах, а в полярной системе координат. Если тело имеет форму кругового цилиндра или ограничено радиальными и круговыми сечениями цилиндра, плоскую задачу проще решать не в прямоугольных, а в полярных координатах.

1. Общие уравнения плоской задачи в полярных координатах

При решение плоской задачи встречаются тела, ограниченные поверхностями кругового цилиндра и радиально расходящимися плоскостями. В этих случаях переход от декартовой системы координат к полярной значительно упрощаем наше решение. В полярной системе координат положение абсолютно любой точки плоскости можно определить двумя величинами: радиус-вектором r и полярным углом [pic 2] (Рисунок 2.1). Совместим полюс полярной системы координат ( r , [pic 3] ) с началом декартовой системы координат (x,y), а полярную ось совместим с осью абсцисс Ox ( Рисунок 2.1). А теперь выясним связь между координатами т.М в полярной и декартовой системах координат:
x = rcos [pic 4] ; y = rsin [pic 5] . (2.1)

Обратные зависимости имеют вид:

r = ; cos [pic 7] = = ; sin [pic 10] = = (2.2) [pic 6][pic 8][pic 9][pic 11][pic 12]

1. Основные уравнения равновесия

Вырежем из пластинки бесконечной малый элемент (Рисунок 3.1) двумя радиальными плоскостями, образующими угол d θ, и двумя цилиндрическими поверхностями с радиусами r и r+ dr.

Введем обозначения для напряжений:

σ r — нормальные напряжения по направлению радиуса, или радиальные напряжения;

[pic 14] — нормальные напряжения в перпендикулярном направлении, или тангенциальные напряжения;

Лекция 1. Основы теории упругости

1.1 Основные положения, допущения и обозначения

Теория упругости имеет целью аналитическое изучение напряженно-деформированного состояния упругого тела. С помощью теории упругости могут быть проверены решения, полученные с использованием допущений сопротивления ма­териалов, и установлены границы применимости этих решений. Иногда разделы теории упругости, в которых, как и в сопротив­лении материалов, рассматривается вопрос о пригодности де­тали, но с использованием достаточно сложного математического аппарата (расчет пластин, оболочек, массивов), относят к при­кладной теории упругости.

В настоящей главе изложены основные понятия математиче­ской линейной теории упругости. Применение математики к опи­санию физических явлений требует их схематизации. В математической теории упругости задачи решаются с возможно меньшим числом допущений, что усложняет мате­матические приемы, применяемые для решения. В линейной тео­рии упругости предполагается существование линейной зави­симости между составляющими напряжениями и деформациями. Для ряда материалов (резина, некоторые сорта чугуна) такая зависимость даже при малых деформациях не может быть принята: диаграмма s — e в пределах упругости имеет одинако­вые очертания как при нагружении , так и при разгрузке, но в обоих случаях криволинейна. При исследовании таких материалов необходимо пользоваться зависимостями нелинейной теории упру­гости.

В математической линейной теории упругости исходят из следующих допущений:

1. О непрерывности ( сплошности ) среды. При этом атомистическая структура вещества или наличие каких-либо пустот не учитывается.

2. О естественном состоянии, на основании которого началь­ное напряженное (деформированное) состояние тела, возникшее до приложения силовых воздействий, не учитывается, т. е. предполагается, что в момент нагружения тела деформации и напряжения в любой его точке равны нулю. При наличии на­чальных напряжений это допущение будет справедливым, если только к результирующим напряжениям (сумме начальных и возникших от них из воздействий) могут быть применены зависимости линейной теории упругости.

3. Об однородности, на основании которого предполагается, что состав тела одинаков во всех точках. Если применительно к металлам это допущение не дает больших погрешностей, то в от­ношении бетона при рассмотрении малых объемов оно может при­вести к значительным погрешностям.

4. О шаровой изотропности , на основании которого считается, что механические свойства материала одинаковы по всем направ­лениям. Кристаллы металла не обладают таким свойством, но для металла в целом, состоящего из большого числа мелких кри­сталлов, можно считать, что эта гипотеза справедлива. Для ма­териалов, обладающих различными механическими свойствами в разных направлениях, как, например, для слои­стых пластиков, разработана теория упругости ортотропных и анизотропных материалов.

5. Об идеальной упругости, на основании которого предпола­гается полное исчезновение деформации после снятия нагрузки. Как известно, в реальных телах при любом нагружении возникает остаточная деформация. Поэтому допущение следует считать при­менимым, если остаточная деформация не превышает условно заданной нормы.

6. О линейной зависимости между составляющими деформа­циями и напряжениями.

7. О малости деформаций, на основании которого предпола­гается, что относительные линейные и угловые деформации малы по сравнению с единицей. Для таких материалов, как резина, или таких элементов, как спиральные пружины, создана теория больших упругих деформаций.

При решении задач теории упругости пользуются теоремой о единственности решения: если заданные внешние поверхностные и объемные силы находятся в равновесии, им соответствует одна единственная система на­пряжений и перемещений. Положен ие о е динственности решения справедливо, если только справедливы допущение о естественном состоянии тела (иначе возможно бесчисленное количество решений) и допущение о линейной зависимости между деформациями и внешними силами.

При решении задач теории упругости часто пользуются принци­пом Сен-Венана: если внешние силы, приложенные на небольшом участке упругого тела, заменить действующей на том же участке статически эквивалентной си­стемой сил (имеющей тот же главный вектор и тот же главный момент), то эта замена вызовет лишь изменение местных де­формаций.

В точках, достаточно удаленных от мест приложения внешних нагрузок, напряжения мало зависят от способа их приложения. Нагрузка, которая в курсе сопротивления мате­риалов схематически выражалась на основании принципа Сен-Венана в виде силы или сосредоточенного момента, на самом деле представляет собой нормальные и касательные напряжения, распределенные тем или иным способом на определенном участке поверхности тела. При этом одной и той же силе или паре сил может соответствовать различное распределение напряже­ний. На основании принципа Сен-Венана можно считать, что из­менение усилий на участке поверхности тела почти не отражается на напряжениях в точках, удаленных на достаточно большое расстояние от места приложения этих усилий (по сравнению с линейными размерами нагруженного участка).

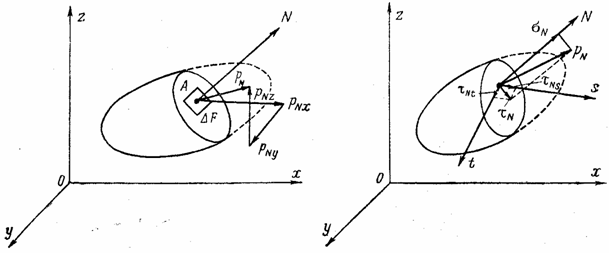
Положение исследуемой площадки, выделенной в теле (рис. 1), определяется направляющими косинусами нормали N к пло­щадке в выбранной системе прямоугольных осей координат х , у и z .

Если Р — равнодействующая внутренних сил, действующих по элементарной площадке , выделенной у точки А , то полное напряжение р _N в этой точке по площадке с нормалью N опре­деляется как предел отношения в следующей форме:

.

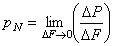
Вектор р _N можно разложить в пространстве на три взаимно перпендикулярные составляющие.

1. На составляющие р _Nx , р _Ny и р _Nz по направлениям трех осей (рис. 1, а). Эти состав­ляющие положительны, если совпадают по направлению с поло­жительными направлениями соответствующих осей. Согласно рис. 1, а

. (1.1,а)

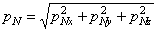
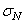
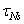
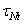
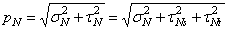
2. На составляющие , и по направлениям нормали к площадке (нормальное напряжение) и двух взаимно перпенди­кулярных осей s и t (рис. 1,б), лежащих в плоскости площадки (касательные напряжения). Согласно рис.1, б

. (1.1,б)

Если сечение тела или площадка параллельны одной из плоскостей координат, например у0 z (рис. 2), то нормалью к этой площадке будет третья ось координат х и составляющие напря­жения будут иметь обозначения , и .

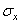
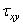
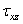
Нормальное напряжение положительно, если оно растяги­вающее, и отрицательно, если оно сжимающее. Знак касатель­ного напряжения определяется с помощью следующего правила: если положительное (растягивающее) нормальное напряжение по площадке дает положительную проекцию, то касательное на­пряжение по той же площадке считается положительным при условии, что оно тоже дает положительную проекцию на соот­ветствующую ось; если же растягивающее нормальное напря­жение дает отрицательную проекцию, то положительное касательное напряжение тоже должно давать отрицательную про­екцию на соответствующую ось.

На рис. 3, например, все составляющие напряжения, дейст­вующие по граням элементарного параллелепипеда, совпадаю­щим с плоскостями координат, положительны.

Чтобы определить напряженное состояние в точке упругого тела, необходимо знать полные напряжения р _N по трем взаимно перпендикулярным площадкам, проходящим через эту точку. Так как каждое полное напряжение можно разложить на три составляющие, напряженное состояние будет определено, если будут известны девять составляющих напряжений. Эти составляю­щие можно записать в виде матрицы

,

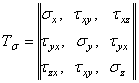
называемой матрицей компонентов тензора напряжений в точке.

В каждой горизонтальной строчке матрицы записаны три со­ставляющих напряжения, действующих по одной площадке, так как первые значки (название нормали) у них одинаковые. В каждом вертикальном столбце тензора записаны три напря­жения, параллельных одной и той же оси, так как вторые значки (название оси, параллельно которой действует напряжение) у них одинаковые.

1.2 Уравнения равновесия элементарного параллелепипеда и элементарного тетраэдра

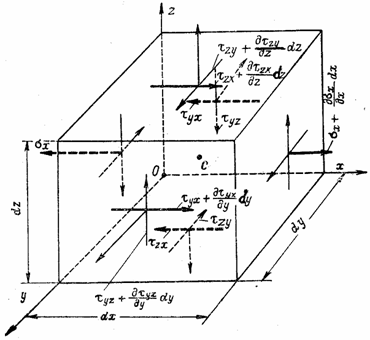
Выделим у исследуемой точки А (с координатами х , у и z ) напря­женного упругого тела тремя взаимно перпендикулярными па­рами плоскостей элементарный параллелепипед с размерами ребер dx , dy и dz (рис. 2). По каждой из трех взаимно перпен­дикулярных граней, примыкающих к точке А (ближайших к пло­скостям координат), будут действовать три составляющих напря­жения — нормальное и два касательных. Считаем, что по граням, примыкающим к точке А , они положительны.

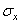
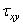
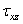
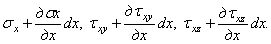
При переходе от грани, проходящей через точку А , к парал­лельной грани напряжения меняются и получают приращения. Например, если по грани CAD , проходящей через точку А , дей­ствуют составляющие напряжения = f ₁ ( x , y , z ), = f ₂ ( x , y , z ,), = f ₃ ( x , y , z ,), то по параллельной грани, вслед­ствие приращения только одной координаты х при переходе от одной грани к другой, будут действовать составляющие напря­жения Можно определить напряжения на всех гранях элементарного паралле­лепипеда, как показано на рис. 3.

Кроме напряжений, приложенных к граням элементарного параллелепипеда, на него действуют объемные силы: силы веса, инерционные. Обозначим проекции этих сил, отнесенных к единице объема, на оси координат через X, У и Z. Если приравнять нулю сумму проекций на ось х всех нормальных, касательных и объемной сил, дейст­вующих на элементарный параллелепипед, то после сокращения на произведение dxdydz получим уравнение

.

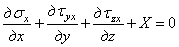
Составив аналогичные уравнения проекций сил на оси у и z , напишем три дифференциальных уравнения равновесия элементар­ного параллелепипеда, полученных Коши,

. (1.2)

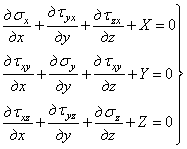
При уменьшении размеров параллелепипеда до нуля он прев­ращается в точку, а 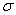и представляют собой составляющие напряжения по трем взаимно перпендикулярным площадкам, проходящим через точку А.

Если приравнять нулю сумму моментов всех сил, действующих на элементарный параллелепипед, относительно оси x _c , парал­лельной оси х и проходящей через его центр тяжести, получим уравнение

или, с учетом того, что второй и четвертый члены уравнения выс­шего порядка малости по сравнению с остальными, после сокра­щения на dxdydz

или .

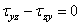
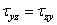
Составив аналогичные уравнения моментов относительно цен­тральных осей у _c и z_c , получим три уравнения закона парности касательных напряжений

, , . (1.3)

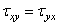
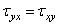
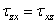
Этот закон формулируется так: касательные напряжения, действующие по взаимно перпендикулярным площадкам и направ­ленные перпендикулярно к линии пересечения площадок, равны по величине и одинаковы по знаку.

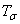
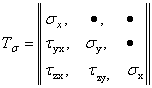
Таким образом, из девяти составляющих напряжений матрицы тензора шесть попарно равны друг другу, и для определения напряженного состояния в точке достаточно найти лишь следую­щие шесть составляющих напряжений:

.

Но составленные условия равновесия дали нам всего лишь три уравнения (1.2), из которых шесть неизвестных найдены быть не могут. Таким образом, прямая задача определения напряжен­ного состояния в точке в общем случае статически неопределима. Для раскрытия этой статической неопределимости необходимы дополнительные геометрические и физические зависимости.

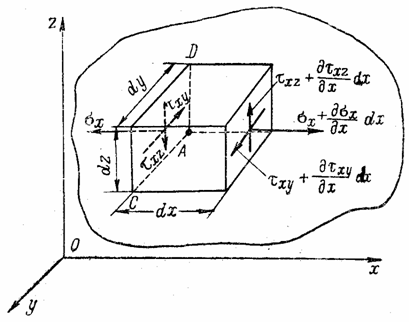
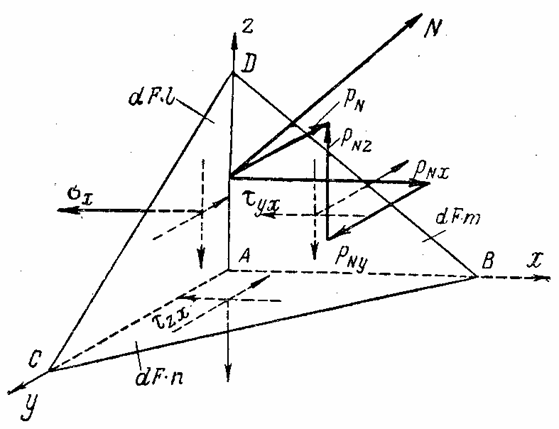
Рассечем элементарный параллелепипед у точки А плоскостью, наклоненной к его граням; пусть нормаль N к этой плоскости имеет направляющие косинусы l , т и п. Полу­чившаяся геометрическая фигура (рис. 4) представляет собой пирамиду с треугольным основанием — элементарный тетраэдр. Будем считать, что точка А совпадает с началом координат, а три взаимно перпендикулярные грани тетраэдра — с плоскостями координат.

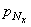
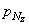
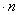
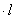
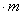
Составляющие напряжения, действующие по этим граням тетраэдра, будем считать положительными. Они показаны на рис. 4. Обозначим через и проекции полного напря­жения p_N , действующего по наклонной грани BCD тетраэдра, на оси х , у и z . Площадь наклонной гра­ни BCD обозначим dF . Тогда площадь грани АВС будет dF , грани ACD — dF и грани А D В — dF .

Составим уравнение равновесия тетраэдра, спроектировав все силы, действующие по его гра­ням, на ось х ; проекция объемной силы в уравне­ние проекций не входит, так как представляет собой величину высшего порядка малости по сравнению с проекциями поверхностных сил:

,

.

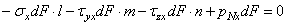
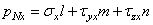
Составив уравнения проекции сил, действующих на тетраэдр, на оси у и z , получим еще два аналогичных уравнения. В результате будем иметь три уравнения равновесия элементар­ного тетраэдра

. (1.4)

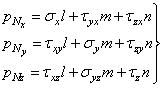
По известным трем проекциям найдем полное напряжение

. (1.5)

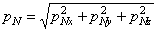
Разделим пространственное тело произвольной формы систе­мой взаимно перпендикулярных плоскостей хОу , y О z и хО z (рис. 5) на ряд элементарных параллелепипедов. У поверхности тела при этом образуются элементарные тетраэдры, (криволинейные участки по­верхности ввиду их малости можно заменить плоскостями). 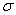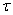В та­ком случае р _N будет представлять нагрузку на поверхности, а уравнения (1.4) будут связывать эту нагрузку с напряжениями и в теле, т. е. будут представлять граничные условия задачи теории упругости. Условия, определяемые этими уравнениями, называют условиями на поверхности.

Следует отметить, что в теории упругости внешние нагрузки представляются нормальными и касательными напряжениями, приложенными по какому-либо закону к площадкам, совпадаю­щим с поверхностью тела.

1.3 Нормальные и касательные напряжения по наклонной площадке

Рассмотрим элементарный тетраэдр ABCD , три грани которого параллельны координатным плоскостям, а нормаль N к четвертой грани составляет с координатными осями углы, косинусы ко­торых равны l , т и п (рис. 6). Будем считать заданными составляющие нормальные и касательные напряжения, действующие по площадкам, лежащим в координатных плоскостях, и определим напряжения на площадке BCD . Выберем новую систему прямо­угольных осей координат х ₁ , y ₁ и z ₁, так чтобы ось х₁ совпадала с нормалью N , а оси у₁ и z ₁ лежали в плоскости площадки BCD . Каждая из этих осей будет иметь в системе осей x , y , z свои направляющие косинусы, указанные в табл. 1.