Уравнения регрессии и способы их построения

Уравнение регрессии: Что это такое и как его использовать

Уравнение регрессии: Обзор

Уравнение регрессии используется в статистике для того, чтобы выяснить, какая связь, если таковая существует, существует между наборами данных. Например, если каждый год измерять рост ребенка, то можно обнаружить, что он растет примерно на 3 дюйма в год. Эта тенденция (которая растет на 3 дюйма в год) может быть смоделирована с помощью уравнения регрессии. Фактически, большинство вещей в реальном мире (от цен на газ до ураганов) можно смоделировать с помощью некоего уравнения, что позволяет нам предсказывать будущие события.

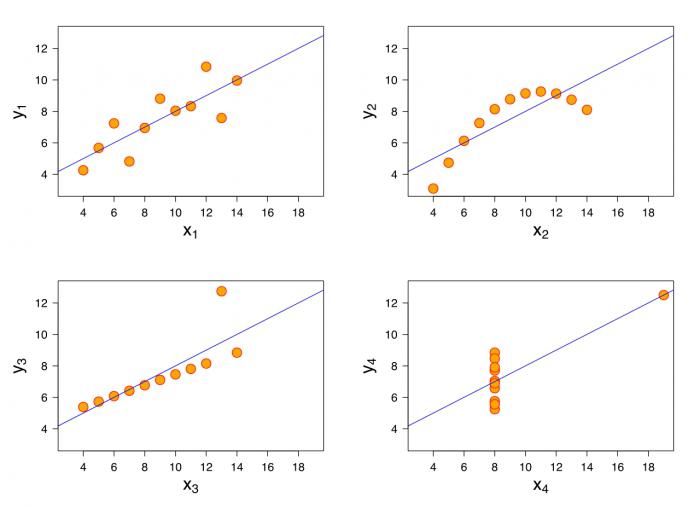
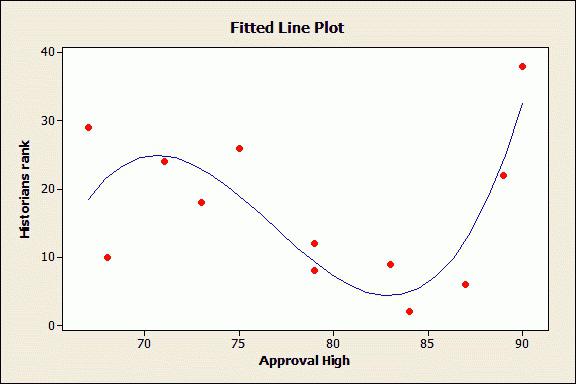
Линия регрессии – это “самая подходящая” линия для ваших данных. По сути, вы рисуете линию, которая наилучшим образом представляет точки данных. Она представляет собой среднее арифметическое того, где выравниваются все точки. В линейной регрессии линия регрессии является абсолютно прямой линией:

Линия регрессии представлена уравнением. В данном случае уравнение равно -2.2923x + 4624.4. Это означает, что если бы вы строили график уравнения -2.2923x + 4624.4, то линия была бы грубой аппроксимацией для ваших данных.

Не очень распространено, чтобы все точки данных действительно попадали на линию регрессии. На рисунке выше точки немного рассеяны вокруг линии. На следующем изображении точки падают на линию. Изогнутая форма этой линии является результатом полиномиальной регрессии, которая укладывает точки в уравнение полинома.

Уравнение регрессии: Что это такое и как его использовать

Статистические определения > Что такое уравнение регрессии?

Уравнение регрессии: Обзор

Уравнение регрессии используется в статистике для того, чтобы выяснить, какая связь, если таковая существует, существует между наборами данных. Например, если каждый год измерять рост ребенка, то можно обнаружить, что он растет примерно на 3 дюйма в год. Эта тенденция (которая растет на 3 дюйма в год) может быть смоделирована с помощью уравнения регрессии. Фактически, большинство вещей в реальном мире (от цен на газ до ураганов) можно смоделировать с помощью некоего уравнения, что позволяет нам предсказывать будущие события.

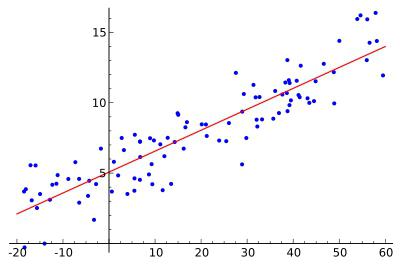
Линия регрессии – это “самая подходящая” линия для ваших данных. По сути, вы рисуете линию, которая наилучшим образом представляет точки данных. Она представляет собой среднее арифметическое того, где выравниваются все точки. В линейной регрессии линия регрессии является абсолютно прямой линией:

Линия линейной регрессии.

Линия регрессии представлена уравнением. В данном случае уравнение равно -2.2923x + 4624.4. Это означает, что если построить график уравнения -2.2923x + 4624.4, то линия будет представлять собой грубую аппроксимацию для Ваших данных.

Не очень распространено, чтобы все точки данных действительно попадали на линию регрессии. На рисунке выше точки немного рассеяны вокруг линии. На следующем изображении точки падают на линию. Изогнутая форма этой линии является результатом полиномиальной регрессии, которая укладывает точки в уравнение полинома.

В результате полиномиальной регрессии получается кривая линия.

Результатом полиномиальной регрессии является кривая линия.

Регрессия и линии прогнозирования

Регрессия полезна, так как позволяет делать прогнозы о данных. Первый график выше – с 1995 по 2015 год. Если вы хотите предсказать, что произойдет в 2020 году, вы можете поместить его в уравнение:

Отрицательное выпадение осадков не имеет особого смысла, но можно сказать, что до 2020 года осадки выпадут на 0 дюймов. Согласно этой конкретной линии регрессии, рано или поздно это произойдет в 2018 году:

Для чего нужно уравнение регрессии?

Уравнения регрессии могут помочь вам понять, подходят ли ваши данные для уравнения. Это чрезвычайно полезно, если вы хотите сделать прогноз на основе своих данных – как будущих прогнозов, так и указаний на прошлое поведение. Например, вы можете захотеть узнать, сколько ваших сбережений будет стоить в будущем. Или, возможно, вы захотите предсказать, сколько времени понадобится на выздоровление от болезни.

Существуют различные типы уравнений регрессии. К наиболее распространенным относятся экспоненциальная линейная регрессия и простая линейная регрессия (для адаптации данных к экспоненциальному уравнению или линейному уравнению). В элементарной статистике уравнение регрессии, с которым вы, скорее всего, столкнетесь, является линейной формой.

Расчет линейной регрессии

Есть несколько способов найти линию регрессии, даже вручную и с помощью технологий, таких как Excel (см. ниже). Поиск линии регрессии очень скучен вручную. Следующее видео иллюстрирует шаги:

Линию регрессии также можно найти в калькуляторах TI:

TI 83 Регрессия.

Как выполнять регрессию TI-89.

Уравнение линейной регрессии показано ниже.

Для того, чтобы данные вписались в уравнение, необходимо сначала понять, какая общая схема подходит для данных. Общие шаги для выполнения регрессии включают в себя составление дисперсионной диаграммы, а затем гипотезу о том, какой тип уравнения может быть наиболее подходящим. Затем можно выбрать наилучшее уравнение регрессии для задания.

Однако, как видно на следующем рисунке, не всегда легко выбрать подходящее уравнение регрессии, особенно при работе с реальными данными. Иногда получаются “шумные” данные, которые, кажется, не подходят ни под одно уравнение. Если большинство данных, кажется, следуют шаблону, вы можете пропустить пропуски. На самом деле, если игнорировать промахи, данные, кажется, моделируются экспоненциальным уравнением.

Уравнение регрессии. Уравнение множественной регрессии

Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.

Определение понятия регрессии

В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).

Какие бывают типы связей между переменными

В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.

Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.

Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.

Виды регрессий

На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.

Гиперболическая, линейная и логарифмическая

Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.

Множественная и нелинейная

Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х₁ , х₂ . х_с)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.

Обратные и парные виды регрессий

Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.

Понятие корреляции

Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.

Методы

Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.

Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.

В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.

Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).

Корреляция для множественной регрессии

Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.

Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.

Метод наименьших квадратов

Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.

Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.

Параметры уравнений

Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.

Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.

Сгруппированные данные

Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.

Множественное парное уравнение регрессии: оценка важности связи

Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x₁,x₂,…,x_m)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.

Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.

Линейная функция изображается в форме такой взаимосвязи: у = а₀ + a₁х₁ + а₂х₂,+ . + a_mx_m. При этом _а2, a_m, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.

Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах₁ b1 х₂ b2 . x_m bm . В данном случае показатели b₁, b₂. b_m – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.

Какие факторы необходимо учитывать при построении множественной регрессии

Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.

Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:

• Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
• Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
• В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.

Методы построения

Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:

• Способ исключения.
• Способ включения.
• Пошаговый анализ регрессии.

Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.

Методы многомерного анализа

Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.

Справка

Набор инструментов Пространственная статистика (Spatial Statistics) предоставляет эффективные инструменты количественного анализа пространственных структурных закономерностей. Инструмент Анализ горячих точек (Hot Spot Analysis) , например, поможет найти ответы на следующие вопросы:

• Есть ли в США места, где постоянно наблюдается высокая смертность среди молодежи?
• Где находятся «горячие точки» по местам преступлений, вызовов 911 (см. рисунок ниже) или пожаров?
• Где находятся места, в которых количество дорожных происшествий превышает обычный городской уровень?

Анализ данных звонков в службу 911, показывающий горячие точки (красным), холодные точки (синим) и локализацию пожарных/полиции, ответственных за реагирование (зеленые круги)

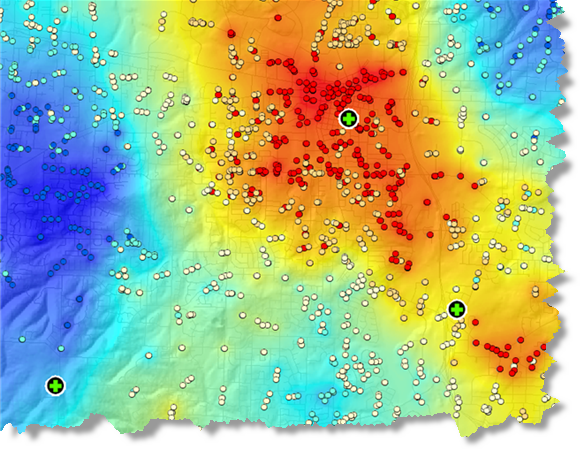
Каждый из вопросов спрашивает «где»? Следующий логический вопрос для такого типа анализа – «почему»?

• Почему в некоторых местах США наблюдается повышенная смертность молодежи? Какова причина этого?
• Можем ли мы промоделировать характеристики мест, на которые приходится больше всего преступлений, звонков в 911, или пожаров, чтобы помочь сократить эти случаи?
• От каких факторов зависит повышенное число дорожных происшествий? Имеются ли какие-либо возможности для снижения числа дорожных происшествий в городе вообще, и в особо неблагополучных районах в частности?

Пространственные отношения

Регрессионный анализ позволяет вам моделировать, проверять и исследовать пространственные отношения и помогает вам объяснить факторы, стоящие за наблюдаемыми пространственными структурными закономерностями. Вы также можете захотеть понять, почему люди постоянно умирают молодыми в некоторых регионах страны, и какие факторы особенно влияют на особенно высокий уровень диабета. При моделирование пространственных отношений, однако, регрессионный анализ также может быть пригоден для прогнозирования. Моделирование факторов, которые влияют на долю выпускников колледжей, на пример, позволяют вам сделать прогноз о потенциальной рабочей силе и их навыках. Вы также можете использовать регрессионный анализ для прогнозирования осадков или качества воздуха в случаях, где интерполяция невозможна из-за малого количества станций наблюдения (к примеру, часто отсутствую измерительные приборы вдоль горных хребтов и в долинах).

МНК (OLS) – наиболее известный метод регрессионного анализа. Это также подходящая отправная точка для всех способов пространственного регрессионного анализа. Данный метод позволяет построить глобальную модель переменной или процесса, которые вы хотите изучить или спрогнозировать (уровень смертности/осадки). Он создает уравнение регрессии, отражающее происходящий процесс. Географически взвешенная регрессия (ГВР) – один из нескольких методов пространственного регрессионного анализа, все чаще использующегося в географии и других дисциплинах. Метод ГВР (географически взвешенная регрессия) создает локальную модель переменной или процесса, которые вы прогнозируете или изучаете, применяя уравнение регрессии к каждому пространственному объекту в наборе данных. При подходящем использовании, эти методы являются мощным и надежным статистическим средством для проверки и оценки линейных взаимосвязей.

Линейные взаимосвязи могут быть положительными или отрицательными. Если вы обнаружили, что количество поисково-спасательных операций увеличивается при возрастании среднесуточной температуры, такое отношение является положительным; имеется положительная корреляция. Другой способ описать эту положительную взаимосвязь – сказать, что количество поисково-спасательных операций уменьшается при уменьшении среднесуточной температуры. Соответственно, если вы установили, что число преступлений уменьшается при увеличении числа полицейских патрулей, данное отношение является отрицательным. Также, можно выразить это отрицательное отношение, сказав, что количество преступлений увеличивается при уменьшении количества патрулей. На рисунке ниже показаны положительные и отрицательные отношения, а также случаи, когда две переменные не связаны отношениями:

Диаграммы рассеивания: положительная связь, отрицательная связь и пример с 2 не связанными переменными.

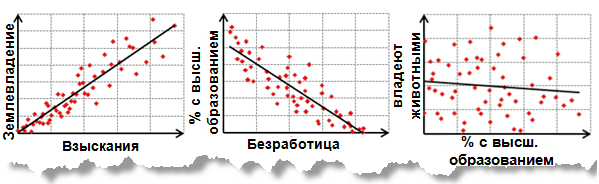
Корреляционные анализы, и связанные с ними графики, отображенные выше, показывают силу взаимосвязи между двумя переменными. С другой стороны, регрессионные анализы дают больше информации: они пытаются продемонстрировать степень, с которой 1 или более переменных потенциально вызывают положительные или негативные изменения в другой переменной.

Применения регрессионного анализа

Регрессионный анализ может использоваться в большом количестве приложений:

• Моделирование числа поступивших в среднюю школу для лучшего понимания факторов, удерживающих детей в том же учебном заведении.
• Моделирование дорожных аварий как функции скорости, дорожных условий, погоды и т.д., чтобы проинформировать полицию и снизить несчастные случаи.
• Моделирование потерь от пожаров как функции от таких переменных как степень вовлеченности пожарных департаментов, время обработки вызова, или цена собственности. Если вы обнаружили, что время реагирования на вызов является ключевым фактором, возможно, существует необходимость создания новых пожарных станций. Если вы обнаружили, что вовлеченность – главный фактор, возможно, вам нужно увеличить оборудование и количество пожарных, отправляемых на пожар.

Существует три первостепенных причины, по которым обычно используют регрессионный анализ:

• Смоделировать некоторые явления, чтобы лучше понять их и, возможно, использовать это понимание для оказания влияния на политику и принятие решений о наиболее подходящих действиях. Основная цель – измерить экстент, который при изменениях в одной или более переменных связанно вызывает изменения и в другой. Пример. Требуется понять ключевые характеристики ареала обитания некоторых видов птиц (например, осадки, ресурсы питания, растительность, хищники) для разработки законодательства, направленного на защиту этих видов.
• Смоделировать некоторые явления, чтобы предсказать значения в других местах или в другое время. Основная цель – построить прогнозную модель, которая является как устойчивой, так и точной. Пример: Даны прогнозы населения и типичные погодные условия. Каким будет объем потребляемой электроэнергии в следующем году?
• Вы также можете использовать регрессионный анализ для исследования гипотез. Предположим, что вы моделируете бытовые преступления для их лучшего понимания и возможно, вам удается внедрить политические меры, чтобы остановить их. Как только вы начинаете ваш анализ, вы, возможно, имеете вопросы или гипотезы, которые вы хотите проверить:
  • «Теория разбитого окна» указывает на то, что испорченная общественная собственность (граффити, разрушенные объекты и т.д.) притягивает иные преступления. Имеется ли положительное отношение между вандализмом и взломами в квартиры?
  • Имеется ли связь между нелегальным использованием наркотических средств и взломами в квартиры (могут ли наркоманы воровать, чтобы поддерживать свое существование)?
  • Совершаются ли взломы с целью ограбления? Возможно ли, что будет больше случаев в домохозяйствах с большей долей пожилых людей и женщин?
  • Люди больше подвержены риску ограбления, если они живут в богатой или бедной местности?

  Вы можете использовать регрессионный анализ, чтобы исследовать эти взаимосвязи и ответить на ваши вопросы.

Термины и концепции регрессионного анализа

Невозможно обсуждать регрессионный анализ без предварительного знакомства с основными терминами и концепциями, характерными для регрессионной статистики:

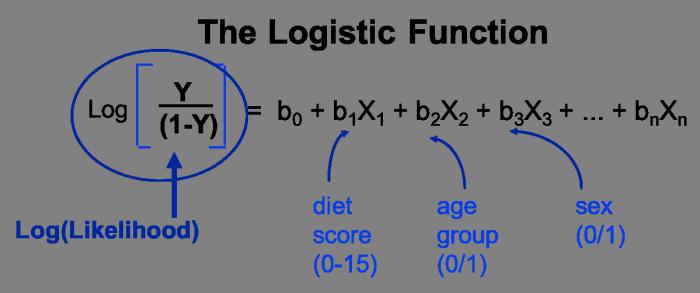
Уравнение регрессии. Это математическая формула, применяемая к независимым переменным, чтобы лучше спрогнозировать зависимую переменную, которую необходимо смоделировать. К сожалению, для тех ученых, кто думает, что х и у это только координаты, независимая переменная в регрессионном анализе всегда обозначается как y, а зависимая – всегда X. Каждая независимая переменная связана с коэффициентами регрессии, описывающими силу и знак взаимосвязи между этими двумя переменными. Уравнение регрессии может выглядеть следующим образом (у – зависимая переменная, Х – независимые переменные, β – коэффициенты регрессии), ниже приводится описание каждого из этих компонентов уравнения регрессии):

Элементы Уравнения регрессии по методу наименьших квадратов

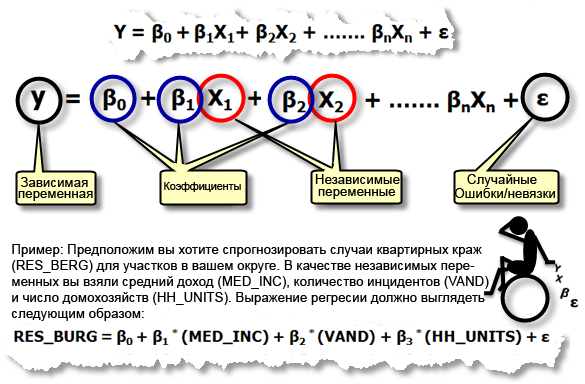
• Зависимая переменная (y) – это переменная, описывающая процесс, который вы пытаетесь предсказать или понять (бытовые кражи, осадки). В уравнении регрессии эта переменная всегда находится слева от знака равенства. В то время, как можно использовать регрессию для предсказания зависимой величины, вы всегда начинаете с набора хорошо известных у-значений и используете их для калибровки регрессионной модели. Известные у-значения часто называют наблюдаемыми величинами.
• Независимые переменные (X) это переменные, используемые для моделирования или прогнозирования значений зависимых переменных. В уравнении регрессии они располагаются справа от знака равенства и часто называются независимыми переменными. Зависимая переменная – это функция независимых переменных. Если вас интересует прогнозирование годового оборота определенного магазина, можно включить в модель независимые переменные, отражающие, например, число потенциальных покупателей, расстояние до конкурирующих магазинов, заметность магазина и структуру спроса местных жителей.
• Коэффициенты регрессии (β) – это коэффициенты, которые рассчитываются в результате выполнения регрессионного анализа. Вычисляются величины для каждой независимой переменной, которые представляют силу и тип взаимосвязи независимой переменной по отношению к зависимой. Предположим, что вы моделируете частоту пожаров как функцию от солнечной радиации, растительного покрова, осадков и экспозиции склона. Вы можете ожидать положительную взаимосвязь между частотой пожаров и солнечной радиацией (другими словами, чем больше солнца, тем чаще встречаются пожары). Если отношение положительно, знак связанного коэффициента также положителен. Вы можете ожидать негативную связь между частотой пожаров и осадками (другими словами, для мест с большим количеством осадков характерно меньше лесных пожаров). Коэффициенты отрицательных отношений имеют знак минуса. Когда взаимосвязь сильная, значения коэффициентов достаточно большие (относительно единиц независимой переменной, с которой они связаны). Слабая взаимосвязь описывается коэффициентами с величинами около 0; β₀ – это пересечение линии регрессии. Он представляет ожидаемое значение зависимой величины, если все независимые переменные равны 0.

P-значения. Большинство регрессионных методов выполняют статистический тест для расчета вероятности, называемой р-значением, для коэффициентов, связанной с каждой независимой переменной. Нулевая гипотеза данного статистического теста предполагает, что коэффициент незначительно отличается от нуля (другими словами, для всех целей и задач, коэффициент равен нулю, и связанная независимая переменная не может объяснить вашу модель). Маленькие величины р-значений отражают маленькие вероятности и предполагают, что коэффициент действительно важен для вашей модели со значением, существенно отличающимся от 0 (другими словами, маленькие величины р-значений свидетельствуют о том, что коэффициент не равен 0). Вы бы сказали, что коэффициент с р-значением, равным 0,01, например, статистически значимый для 99 % доверительного интервала; связанные переменные являются эффективным предсказателем. Переменные с коэффициентами около 0 не помогают предсказать или смоделировать зависимые величины; они практически всегда удаляются из регрессионного уравнения, если только нет веских причин сохранить их.

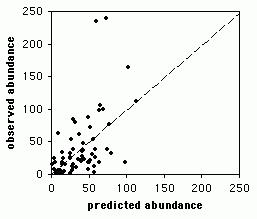
R 2 /R-квадрат: Статистические показатели составной R-квадрат и выровненный R-квадрат вычисляются из регрессионного уравнения, чтобы качественно оценить модель. Значение R-квадрат лежит в пределах от 0 до 100 процентов. Если ваша модель описывает наблюдаемые зависимые переменные идеально, R-квадрат равен 1.0 (и вы, несомненно, сделали ошибку; возможно, вы использовали модификацию величины у для предсказания у). Вероятнее всего, вы увидите значения R-квадрат в районе 0,49, например, можно интерпретировать подобный результат как «Это модель объясняет 49 % вариации зависимой величины». Чтобы понять, как работает R-квадрат, постройте график, отражающий наблюдаемые и оцениваемые значения у, отсортированные по оцениваемым величинам. Обратите внимание на количество совпадений. Этот график визуально отображает, насколько хорошо вычисленные значения модели объясняют изменения наблюдаемых значений зависимых переменных. Просмотрите иллюстрацию. Выверенный R-квадрат всегда немного меньше, чем составной R-квадрат, т.к. он отражает всю сложность модели (количество переменных) и связан с набором исходных данных. Следовательно, выверенный R-квадрат является более точной мерой для оценки результатов работы модели.

Невязки. Существует необъяснимое количество зависимых величин, представленных в уравнении регрессии как случайные ошибки ε. Просмотрите иллюстрацию. Известные значения зависимой переменной используются для построения и настройки модели регрессии. Используя известные величины зависимой переменной (Y) и известные значений для всех независимых переменных (Хs), регрессионный инструмент создаст уравнение, которое предскажет те известные у-значения как можно лучше. Однако предсказанные значения редко точно совпадают с наблюдаемыми величинами. Разница между наблюдаемыми и предсказываемыми значениями у называется невязка или отклонение. Величина отклонений регрессионного уравнения – одно из измерений качества работы модели. Большие отклонения говорят о ненадлежащем качестве модели.

Создание регрессионной модели представляет собой итерационный процесс, направленный на поиск эффективных независимых переменных, чтобы объяснить зависимые переменные, которые вы пытаетесь смоделировать или понять, запуская инструмент регрессии, чтобы определить, какие величины являются эффективными предсказателями. Затем пошаговое удаление и/или добавление переменных до тех пор, пока вы не найдете наилучшим образом подходящую регрессионную модель. Т.к. процесс создания модели часто исследовательский, он никогда не должен становиться простым «подгоном» данных. Он должен учитывать теоретические аспекты, мнение экспертов в этой области и здравый смысл. Вы должным быть способны определить ожидаемую взаимосвязь между каждой потенциальной независимой переменной и зависимой величиной до непосредственного анализа, и должны задать себе дополнительные вопросы, когда эти связи не совпадают.

Примечание:

Если вы никогда не выполняли регрессионный анализ раньше, рекомендуем загрузить Руководство о регрессионному анализу и пройти шаги 1-5.

Особенности регрессионного анализа

Регрессия МНК (OLS) – это простой метод анализа с хорошо проработанной теорией, предоставляющий эффективные возможности диагностики, которые помогут вам интерпретировать результаты и устранять неполадки. Однако, МНК надежен и эффективен, если ваши данные и регрессионная модель удовлетворяют всем предположениям, требуемым для этого метода (смотри таблицу внизу). Пространственные данные часто нарушают предположения и требования МНК, поэтому важно использовать инструменты регрессии в союзе с подходящими инструментами диагностики, которые позволяют оценить, является ли регрессия подходящим методом для вашего анализа, а приведенная структура данных и модель может быть применена.

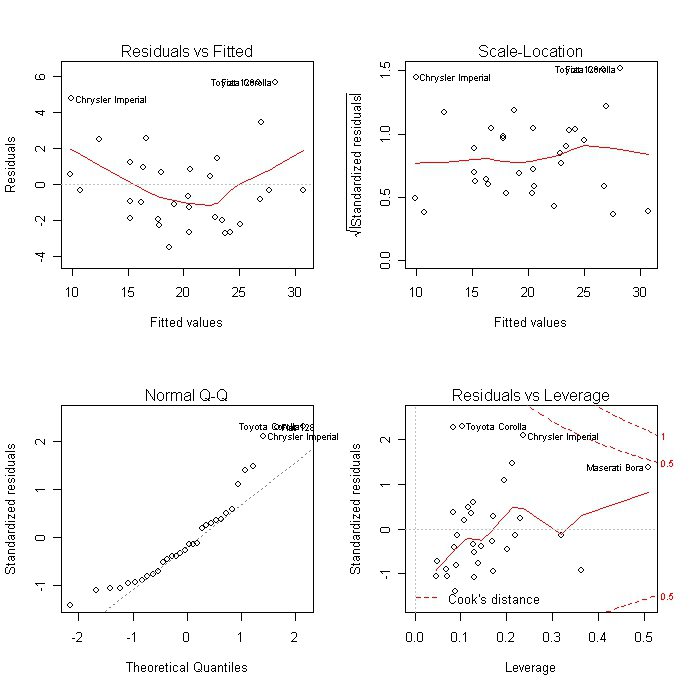
Как регрессионная модель может не работать

Серьезной преградой для многих регрессионных моделей является ошибка спецификации. Модель ошибки спецификации – это такая неполная модель, в которой отсутствуют важные независимые переменные, поэтому она неадекватно представляет то, что мы пытаемся моделировать или предсказывать (зависимую величину, у). Другими словами, регрессионная модель не рассказывает вам всю историю. Ошибка спецификации становится очевидной, когда в отклонениях вашей регрессионной модели наблюдается статистически значимая пространственная автокорреляция , или другими словами, когда отклонения вашей модели кластеризуются в пространстве (недооценки – в одной области изучаемой территории, а переоценки – в другой). Благодаря картографированию невязок регрессии или коэффициентов, связанных с географически взвешенной регрессией , можно обратить внимание на какие-то нюансы, которые вы упустили ранее. Запуск Анализа горячих точек по отклонениям регрессии также может раскрыть разные пространственные режимы, которые можно моделировать при помощи метода наименьших квадратов с региональными показателями или исправлять с использованием географически взвешенной регрессии. Предположим, когда вы картографируете отклонения вашей регрессионной модели, вы видите, что модель всегда заново предсказывает значения в горах, и, наоборот, в долинах, что может значить, что отсутствуют данные о рельефе. Однако может случиться так, что отсутствующие переменные слишком сложны для моделирования или их невозможно подсчитать или слишком трудно измерить. В этих случаях, можно воспользоваться ГВР (географически взвешенной регрессией) или другой пространственной регрессией, чтобы получить хорошую модель.

В следующей таблице перечислены типичные проблемы с регрессионными моделями и инструменты в ArcGIS:

Типичные проблемы с регрессией, последствия и решения

Ошибки спецификации относительно независимых переменных.

Когда ключевые независимые переменные отсутствуют в регрессионном анализе, коэффициентам и связанным с ними р-значениям нельзя доверять.

Создайте карту и проверьте невязки МНК и коэффициенты ГВР или запустите Анализ горячих точек по регрессионным невязкам МНК, чтобы увидеть, насколько это позволяет судить о возможных отсутствующих переменных.

МНК и ГВР – линейные методы. Если взаимосвязи между любыми независимыми величинами и зависимыми – нелинейны, результирующая модель будет работать плохо.

Создайте диаграмму рассеяния, чтобы выявить взаимосвязи между показателями в модели. Уделите особое внимание взаимосвязям, включающим зависимые переменные. Обычно криволинейность может быть устранена трансформированием величин. Просмотрите иллюстрацию. Альтернативно, используйте нелинейный метод регрессии.

Существенные выбросы могут увести результаты взаимоотношений регрессионной модели далеко от реальности, внося ошибку в коэффициенты регрессии.

Создайте диаграмму рассеяния и другие графики (гистограммы), чтобы проверить экстремальные значения данных. Скорректировать или удалить выбросы, если они представляют ошибки. Когда выбросы соответствуют действительности, они не могут быть удалены. Запустить регрессию с и без выбросов, чтобы оценить, как это влияет на результат.

Нестационарность. Вы можете обнаружить, что входящая переменная, может иметь сильную зависимость в регионе А, и в то время быть незначительной или даже поменять знак в регионе B (см. рисунок).

Если взаимосвязь между вашими зависимыми и независимыми величинами противоречит в пределах вашей области изучения, рассчитанные стандартные ошибки будут искусственно раздуты.

Инструмент МНК в ArcGIS автоматически тестирует проблемы, связанные с нестационарностью (региональными вариациями) и вычисляет устойчивые стандартные значения ошибок. Просмотрите иллюстрацию. Когда вероятности, связанные с тестом Koenker, малы (например, Географически взвешенная регрессия .

Мультиколлинеарность. Одна или несколько независимых переменных излишни. Просмотрите иллюстрацию.

Мультиколлинеарность ведет к переоценке и нестабильной/ненадежной модели.

Инструмент МНК в ArcGIS автоматически проверяет избыточность. Каждой независимой переменной присваивается рассчитанная величина фактора, увеличивающего дисперсию. Когда это значение велико (например, > 7,5), избыток является проблемой и излишние показатели должны быть удалены из модели или модифицированы путем создания взаимосвязанных величин или увеличением размера выборки. Просмотрите иллюстрацию.

Противоречивая вариация в отклонениях. Может произойти, что модель хорошо работает для маленьких величин, но становится ненадежна для больших значений. Просмотрите иллюстрацию.

Когда модель плохо предсказывает некоторые группы значений, результаты будут носить ошибочный характер.

Инструмент МНК в ArcGIS автоматически выполняет тест на несистемность вариаций в отклонениях (называемая гетероскедастичность или неоднородность дисперсии) и вычисляет стандартные ошибки, которые устойчивы к этой проблеме. Когда вероятности, связанные с тестом Koenker, малы (например, 0,05), необходимо учитывать устойчивые вероятности, чтобы определить, является ли независимая переменная статистически значимой или нет. Просмотрите иллюстрацию.

Пространственно автокоррелированные отклонения. Просмотрите иллюстрацию.

Когда наблюдается пространственная кластеризация в отклонениях, полученных в результате работы модели, это означает, что имеется переоценённый тип систематических отклонений, модель работает ненадежно.

Запустите инструмент Пространственная автокорреляция (Spatial Autocorrelation) по отклонениям, чтобы убедиться, что в них не наблюдается статистически значимой пространственной автокорреляции. Статистически значимая пространственная автокорреляция практически всегда является симптомом ошибки спецификации (отсутствует ключевой показатель в модели). Просмотрите иллюстрацию.

Нормальное распределение систематической ошибки. Просмотрите иллюстрацию.

Когда невязки регрессионной модели распределены ненормально со средним, близким к 0, р-значения, связанные с коэффициентами, ненадежны.

Инструмент МНК в ArcGIS автоматически выполняет тест на нормальность распределения отклонений. Когда статистический показатель Jarque-Bera является значимым (например, 0,05), скорее всего в вашей модели отсутствует ключевой показатель (ошибка спецификации) или некоторые отношения, которые вы моделируете, являются нелинейными. Проверьте карту отклонений и возможно карту с коэффициентами ГВР, чтобы определить, какие ключевые показатели отсутствуют. Просмотр диаграмм рассеяния и поиск нелинейных отношений.

Типичные проблемы с регрессией и их решения

Важно протестировать модель на каждую из проблем, перечисленных выше. Результаты могут быть на 100 % неправильны, если игнорируются проблемы, упомянутые выше.

Примечание:

Если вы никогда не выполняли регрессионный анализ раньше, рекомендуем загрузить Руководство по регрессионному анализу.

Пространственная регрессия

Для пространственных данных характерно 2 свойства, которые затрудняют (не делают невозможным) применение традиционных (непространственных) методов, таких как МНК:

• Географические объекты довольно часто пространственно автокоррелированы. Это означает, что объекты, расположенные ближе друг к другу более похожи между собой, чем удаленные объекты. Это создает переоцененный тип систематических ошибок для традиционных моделей регрессии.
• География важна, и часто наиболее важные процессы нестационарны. Эти процессы протекают по-разному в разных частях области изучения. Эта характеристика пространственных данных может относиться как к региональным вариациям, так и к нестационарности.

Настоящие методы пространственной регрессии были разработаны, чтобы устойчиво справляться с этими двумя характеристиками пространственных данных и даже использовать эти свойства пространственных данных, чтобы улучшать моделирование взаимосвязей. Некоторые методы пространственной регрессии эффективно имеют дело с 1 характеристикой (пространственная автокорреляция), другие – со второй (нестационарность). В настоящее время, нет методов пространственной регрессии, которые эффективны с обеими характеристиками. Для правильно настроенной модели ГВР пространственная автокорреляция обычно не является проблемой.

Существует большая разница в том, как традиционные и пространственные статистические методы смотрят на пространственную автокорреляцию. Традиционные статистические методы видят ее как плохую вещь, которая должна быть устранена, т.к. пространственная автокорреляция ухудшает предположения многих традиционных статистических методов. Для географа или ГИС-аналитика, однако, пространственная автокорреляция является доказательством важности пространственных процессов; это интегральная компонента данных. Удаляя пространство, мы удаляем пространственный контекст данных; это как только половина истории. Пространственные процессы и доказательство пространственных взаимосвязей в данных представляют собой особый интерес, и поэтому пользователи ГИС с радостью используют инструменты пространственного анализа данных. Однако, чтобы избежать переоцененный тип систематических ошибок в вашей модели, вы должны определить полный набор независимых переменных, которые эффективно опишут структуру ваших данных. Если вы не можете определить все эти переменные, скорее всего, вы увидите существенную пространственную автокорреляцию среди отклонений модели. К сожалению, вы не можете доверять результатам регрессии, пока все не устранено. Используйте инструмент Пространственная автокорреляция , чтобы выполнить тест на статистически значимую пространственную автокорреляцию для отклонений в вашей регрессии.

Как минимум существует 3 направления, как поступать с пространственной автокорреляцией в невязках регрессионных моделей.

1. Изменять размер выборки до тех пор, пока не удастся устранить статистически значимую пространственную автокорреляцию. Это не гарантирует, что в анализе будет полностью устранена проблема пространственной автокорреляции, но она значительно меньше, когда пространственная автокорреляция удалена из зависимых и независимых переменных. Это традиционный статистический подход к устранению пространственной автокорреляции и только подходит, если пространственная автокорреляция является результатом избыточности данных.
2. Изолируйте пространственные и непространственные компоненты каждой входящей величины, используя методы фильтрации в пространственной регрессии. Пространство удалено из каждой величины, но затем его возвращают обратно в регрессионную модель в качестве новой переменной, отвечающей за пространственные эффекты/пространственную структуру. ArcGIS в настоящее время не предоставляет возможности проведения подобного рода анализа.
3. Внедрите пространственную автокорреляцию в регрессионную модель, используя пространственные эконометрические регрессионные модели. Пространственные эконометрические регрессионные модели будут добавлены в ArcGIS в следующем релизе.

Глобальные модели, подобные МНК, создают уравнения, наилучшим образом описывающие общие связи в данных в пределах изучаемой территории. Когда те взаимосвязи противоречивы в пределах территории изучения, МНК хорошо моделирует эти взаимосвязи. Когда те взаимосвязи ведут себя по-разному в разных частях области изучения, регрессионное уравнение представляет средние результаты, и в случае, когда те взаимосвязи представляют 2 экстремальных значения, глобальное среднее не моделирует хорошо эти значения. Когда ваши независимые переменные испытывают нестационарность (региональные вариации), глобальные модели не подходят, а необходимо использовать устойчивые методы регрессионного анализа. Идеально, можно определить полный набор независимых переменных, чтобы справиться с региональными вариациями в ваших зависимых переменных. Если вы не сможете определить все пространственные переменные, вы снова заметите статистически значимую пространственную автокорреляцию в ваших отклонениях и/или более низкие, чем ожидалось, значения R-квадрат . К сожалению, вы не можете доверять результатам регрессии, пока все не устранено.

Существует как минимум 4 способа работы с региональными вариациями в МНК регрессионных моделях:

1. Включить переменную в модель, которая объяснит региональные вариации. Если вы видите, что ваша модель всегда «перепредсказывает» на севере и «недопредсказывает» на юге, добавьте набор региональных значений:1 для северных объектов, и 0 для южных объектов.
2. Используйте методы, которые включают региональные вариации в регрессионную модель, такие как географически взвешенная регрессия .
3. Примите во внимание устойчивые стандартные отклонения регрессии и вероятности, чтобы определить, являются ли коэффициенты статистически значимыми. См. Интерпретация результатов МНК. ГВР рекомендуется
4. Изменить/сократить размер области изучения так, чтобы процессы в пределах новой области изучения были стационарными (не испытывали региональные вариации).

Для большей информации по использованию регрессионных инструментов, см.: