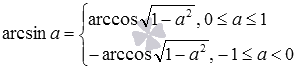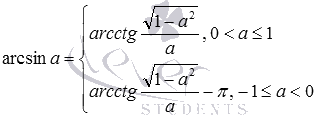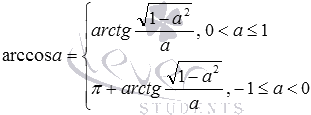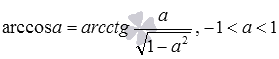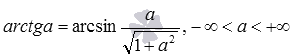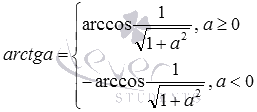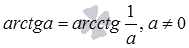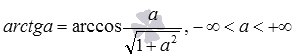Уравнения и неравенства, содержащие обратные тригонометрические функции
Задачи, связанные с обратными тригонометрическими функциями, часто вызывают у школьников старших классов значительные трудности. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как-то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике (включая учебники для классов с углубленным изучением математики) не излагается методика решения даже простейших уравнений и неравенств такого рода. Предлагаемая вашему вниманию статья посвящена методам решения уравнений и неравенств, содержащих обратные тригонометрические функции. Надеемся, что она окажется полезной для учителей, работающих в старших классах – как общеобразовательных, так и математических.
Вначале напомним важнейшие свойства обратных тригонометрических функций.
1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];
arcsin (– x) = – arcsin x (x О [– 1; 1]);
2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];
3 Функция y = arctg x определена и монотонно возрастает на R;
arctg (– x) = – arctg x (x О R);
4 Функция y = arcctg x определена и монотонно убывает на R;
5
Свойства монотонности и ограниченности являются ключевыми при решении многих уравнений и неравенств, содержащих обратные тригонометрические функции. Перейдем к рассмотрению методов решения этих уравнений и неравенств.
I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями
Решение уравнений и неравенств, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность. Напомним, что функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения. Поэтому справедливы следующие равносильные переходы.
1 .
2 .
3 .
4 .
Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).
Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).
Решение. Уравнение равносильно системе
Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.
Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).
Решение. Неравенство равносильно следующему:
Пример 3. Решить неравенство 3arcsin 2x
Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).
Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .
Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:
arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы
Аналогичные равносильные преобразования используются и при решении задач с параметрами.
Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.
Решение. Уравнение равносильно уравнению
Рассмотрим два случая:
1) a = 0. В этом случае система примет вид:
2) a № 0. В этом случае уравнение системы является квадратным. Его корни: 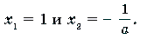
Так как | x | Ј 1, то 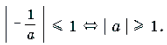
Ответ: при 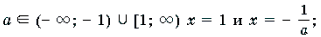
Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).
Решение. Неравенство равносильно системе
Решать последнюю систему можно графо-аналитическим методом, учитывая то, что при a > 


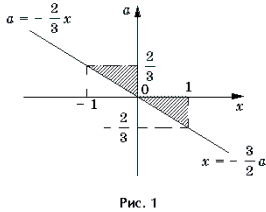


II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями
При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Эта группа задач является чуть более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x0 – решение этого уравнения. Обозначим arcsin f(x0) = arccos g(x0) через a. Тогда sin a = f(x0), cos a = g(x0), откуда f 2 (x0) + g 2 (x0) = 1. Итак, arcsin f(x) = arccos g(x) Ю f 2 (x) + g 2 (x) = 1. (1)
Рассуждая аналогично, можно получить следующие переходы:
Замечание 3. Корнем каждого из уравнений (1)–(4) может быть только такое число x0, для которого f(x0) і 0 и g(x0) і 0. В противном случае множество значений левой и правой частей уравнения не пересекаются.
Пример 9. Решить уравнение
Корень 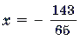
Пример 10. Решить уравнение
Корень x = – 2 является посторонним.
Ответ: .
Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).
Корни вида 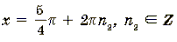
Ответ:
При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций.
Пример 12. Решить неравенство
Решение. Рассмотрим функцию
и решим неравенство f(x) Ј 0 методом интервалов.
1) Найдем D(f). Для этого решим систему
2) Найдем нули f(x). Для этого решим уравнение
Корень x = – 2 является посторонним.
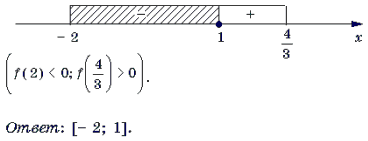
3) Решим неравенство f(x) Ј 0 методом интервалов.
Замечание 4. Заметим, что найдя корень уравнения 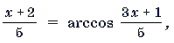

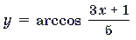
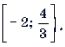
При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,
Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).
Решение. Данное уравнение равносильно системе
Графиком квадратного трехчлена f(x) = 2x 2 – 5ax + 2a2 – 1 является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 2a. Это корень
Ответ: при любом a
III. Замена переменной
Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую замену переменной. При этом следует помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.
Пример 14. Решить уравнение
Решение. Обозначим 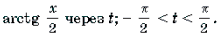
Поскольку
откуда
Ответ:
Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.
Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда
Поскольку 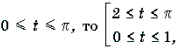
Ответ: [– 1; cos 2] И [cos 1; 1].
Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества
Пример 16. Решить уравнение
Решение. Данное уравнение равносильно следующему:
Пусть arcsin x = t,
Тогда
IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций
Решение некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы.
Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.
Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.
Теорема 3. Если 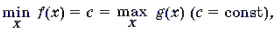
системе
Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.
Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.
Пример 18. Решить уравнение
Решение. Пусть x 2 + x = t. Тогда уравнение примет вид
Функции 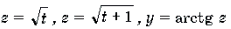
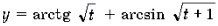
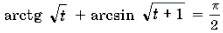
Пример 19. Решить неравенство
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке 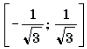
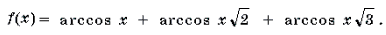
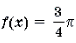
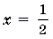
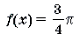
Ответ:
Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .
Решение. Поскольку arcsin 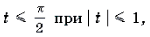
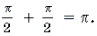
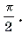
Решение последней системы не представляет труда.
Алгебра
План урока:
Арккосинус
Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:
Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1 1 либо а n ,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1) n окажется равным (– 1), и мы получим вторую серию.
Задание. Решите ур-ние
Задание. Запишите корни ур-ния
Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.
Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:
Ответ: 7π/3 и 8π/3.
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние
Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:
Наконец, решениями ур-ния
Решение уравнений tgx = a и ctgx = a
Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):
Таким образом, у ур-ния tgx = a существует очевидное решение
Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:
Задание. Решите ур-ние
Задание. Запишите формулу корней ур-ния
Далее рассмотрим ур-ние вида
Задание. Решите ур-ние
Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии
Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
Для успешной работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами чисел нужно знать существующие между ними связи. Эти связи удобно записывать в виде формул.
В этой статье мы разберем основные формулы с arcsin, arccos, arctg и arcctg, для удобства работы и запоминания разобьем эти формулы по группам, дадим их вывод и доказательство, а также покажем примеры использования.
Навигация по странице.
Первые четыре блока формул представляют собой основные свойства арксинуса, арккосинуса, арктангенса и арккотангенса числа, в указанной статье сайта www.cleverstudents.ru Вы найдете и доказательство этих формул, и примеры их применения. Здесь мы не будем повторяться, а лишь приведем сами формулы, чтобы они все были в одном месте.
Синус арксинуса, косинус арккосинуса и т.п.
Эти формулы очевидны и напрямую следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса числа. Они показывают, чему равен синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса.
Арксинус синуса, арккосинус косинуса и т.п.
Эти формулы также очевидны и следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса. Они определяют, чему равен арксинус синуса, арктангенс тангенса, арккосинус косинуса и арккотангенс котангенса. Заметим, что стоит быть очень внимательными к указанным условиям, так как если угол (число) α выходит за указанные пределы, то эти формулы использовать нельзя, ибо они дадут неверный результат.
Связи между arcsin, arccos, arctg и arcctg противоположных чисел
Формулы этого блока показывают, как арксинус, арккосинус, арктангенс и арккотангенс отрицательного числа выражаются через arcsin , arccos , arctg и arcctg противоположного ему положительного числа. Эти формулы позволяют избавиться от работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами отрицательных чисел, и перейти к работе с этими аркфункциями от положительных чисел.
Сумма арксинуса и арккосинуса числа, сумма арктангенса и арккотангенса числа
Записанные формулы позволяют выразить арксинус числа через арккосинус этого же числа, арккосинус через арксинус, арктангенс через арккотангенс и арккотангенс через тангенс того же числа.
Синус от арккосинуса, тангенс от арксинуса и иже с ними
На практике очень полезными оказываются формулы, устанавливающие отношения между тригонометрическими функциями и аркфункциями. К примеру, может потребоваться вычислить синус арккосинуса некоторого числа, или тангенс арксинуса. Запишем список формул, позволяющих решать подобные задачи, дальше покажем примеры их применения и приведем доказательства этих формул.
Приведем несколько примеров использования записанных формул. Например, вычислим косинус арктангенса корня из пяти. Соответствующая формула имеет вид 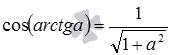
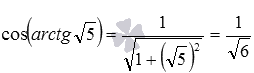
Другой пример: используя формулу синуса арккосинуса вида 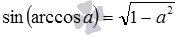
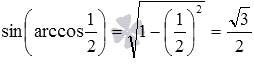
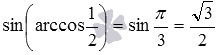
Осталось показать вывод записанных формул.
Формулы, находящиеся в ячейках таблицы на диагонали, есть формулы синуса арксинуса, косинуса арккосинуса и т.д. Они были получены ранее, поэтому не нуждаются в доказательстве, и их мы будем использовать для доказательства остальных формул. Более того, для вывода формул нам еще потребуются основные тригонометрические тождества.
Выведем сначала формулу синуса арккосинуса, синуса арктангенса и синуса арккотангенса. Из основных тригонометрических тождеств 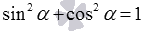
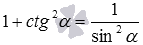
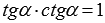
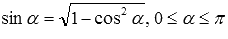
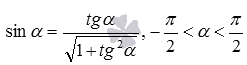
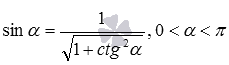
Вот краткая запись вышеперечисленных выкладок:
- так как
, то
;
- так как
, то
;
- так как
, то
.
По аналогии легко вывести формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса:
- так как
, то
;
- так как
, то
;
- так как
, то
.
Теперь покажем вывод формул тангенса арксинуса, тангенса арккосинуса и тангенса арккотангенса:
- так как
, то
при
;
- так как
, то
при
;
- так как
, то
при
.
Формулы котангенса арксинуса, котангенса арккосинуса и котангенса арктангенса легко получить из формул тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса, поменяв в них числитель и знаменатель, так как 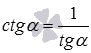
arcsin через arccos, arctg и arcctg; arccos через arcsin, arctg и arcctg и т.п.
Из формул связи тригонометрических и обратных тригонометрических функций, разобранных в предыдущем пункте, можно получить формулы, выражающие одну из аркфункций через другие аркфункции, например, выражающие арксинус одного числа, через арккосинус, арктангенс и арккотангенс другого числа. Перечислим их.
По этим формулам можно заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно:
Вот формулы, выражающие арккосинус через арксинус, арктангенс и арккотангенс:
Формулы арктангенса через арксинус, арккосинус и арккотангенс имеют следующий вид:
Наконец, вот ряд формул с арккотангенсом:
Доказать все записанные формулы можно, отталкиваясь от определений арксинуса, арккосинуса, арктангенса и арккотангенса числа, а также формул из предыдущего пункта.
Для примера, докажем, что 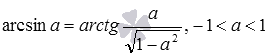
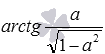
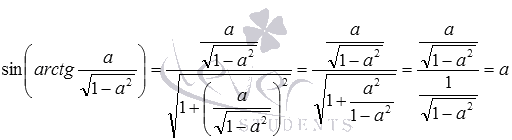
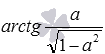
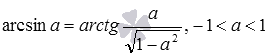
По аналогии можно доказать и остальные формулы, представленные в данном пункте статьи.
В заключение этого пункта покажем пример использования полученных формул. Для примера вычислим с их помощью, чему равен синус арккотангенса минус корня из трех. Обратившись к формуле вида 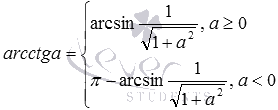
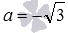
В данном примере мы могли вычислить требуемое значение и непосредственно: 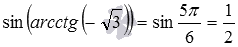
Понятно, что для вычисления требуемого значения мы могли поступить и иначе, воспользовавшись формулой, выражающей синус через котангенс вида 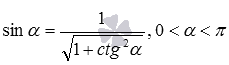
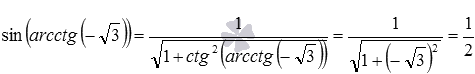
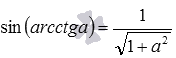
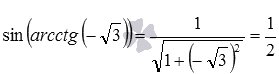
Некоторые другие формулы
Основные формулы тригонометрии и формулы синуса арксинуса, косинуса арккосинуса, тангенса арктангенса и котангенса арккотангенса позволяют вывести ряд формул с arcsin , arccos , arctg и arcctg , еще не упомянутых в данной статье. Но заметим, что они уже достаточно специфичны, и приходится их использовать далеко не часто. Более того, такие формулы удобнее каждый раз выводить, нежели запоминать.
Для примера возьмем формулу половинного угла 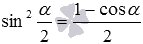
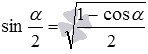

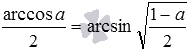
Используя другие тригонометрические формулы, можно обнаружить ряд других связей между arcsin , arccos , arctg и arcctg .
В заключение этого пункта хочется сказать, что практическую пользу представляют даже не столько сами эти специфические формулы, связывающие arcsin , arccos , arctg и arcctg , сколько умения выполнять преобразования, используемых при выводе этих формул. Продолжением темы служит раздел теории преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
http://100urokov.ru/predmety/urok-4-prostejshaya-trigonometriya
http://www.cleverstudents.ru/trigonometry/formulas_with_arcsin_arccos_arctg_arcctg.html
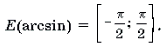
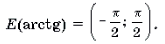
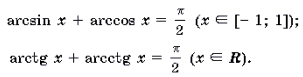
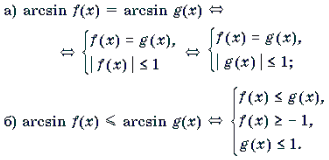
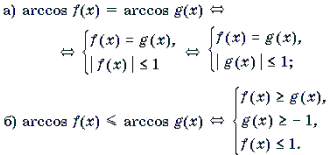
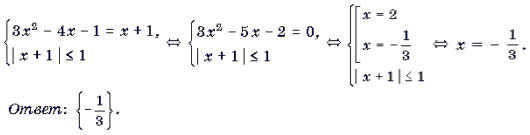
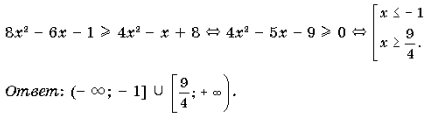
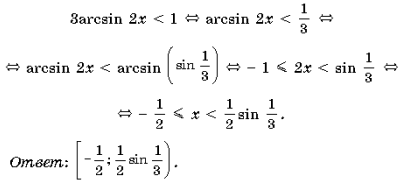
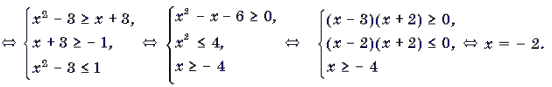
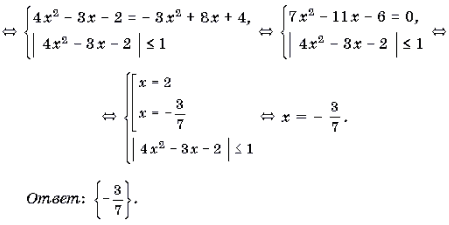
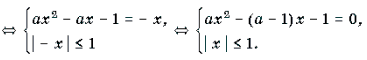
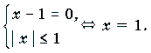
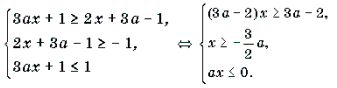
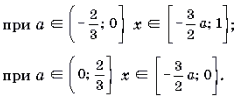
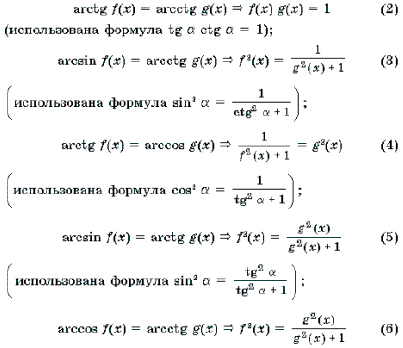
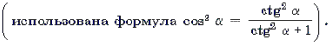
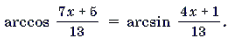
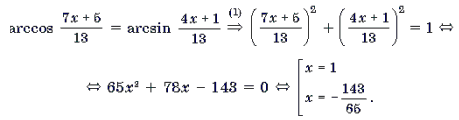
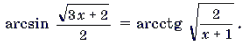
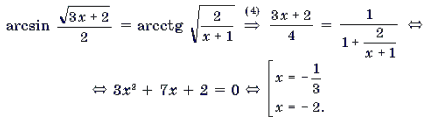
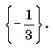
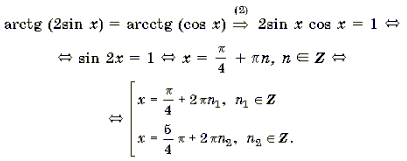
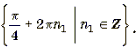
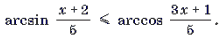
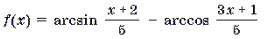
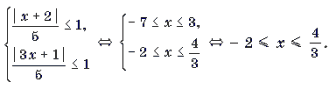
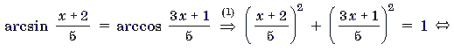
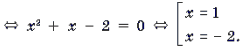
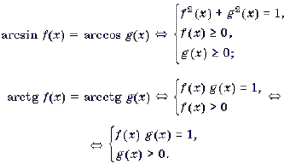
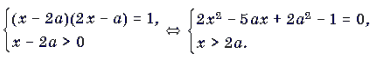
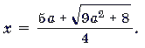
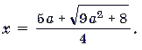
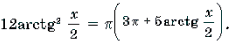
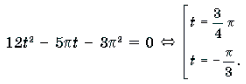
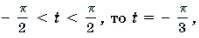
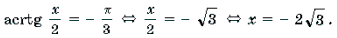
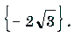
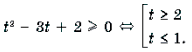
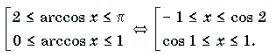
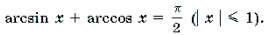
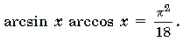
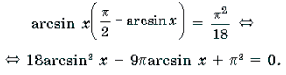
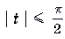
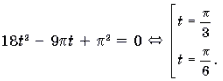
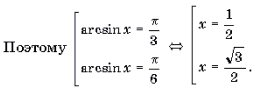
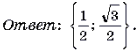
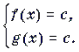
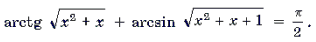

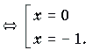
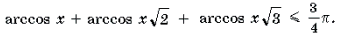
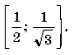
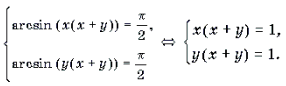
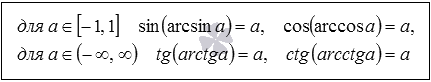

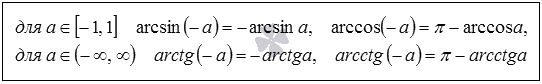
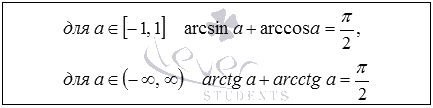

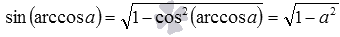 ;
;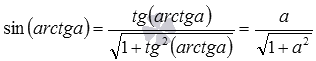 ;
;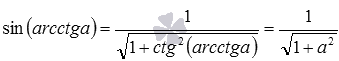 .
.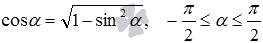 , то
, то 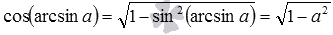 ;
;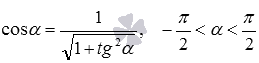 , то
, то 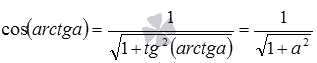 ;
;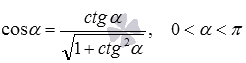 , то
, то 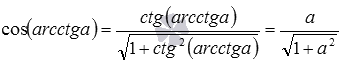 .
.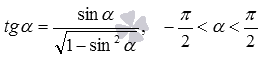 , то
, то 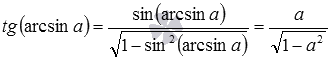 при
при 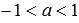 ;
;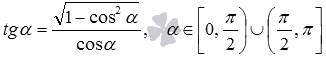 , то
, то 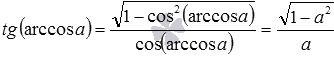 при
при 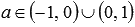 ;
;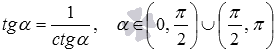 , то
, то 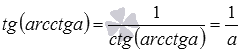 при
при 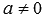 .
.