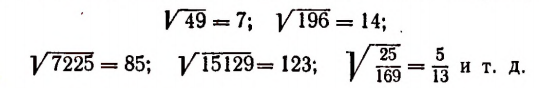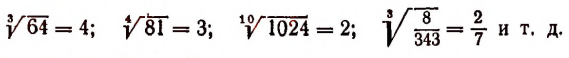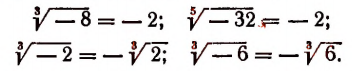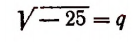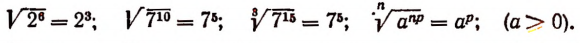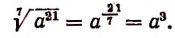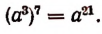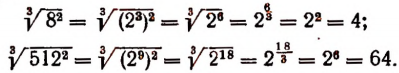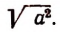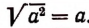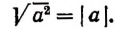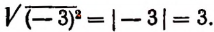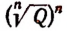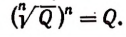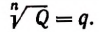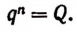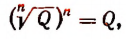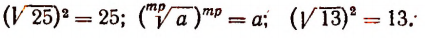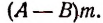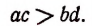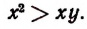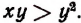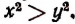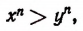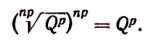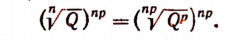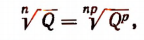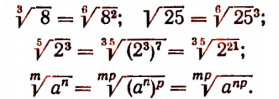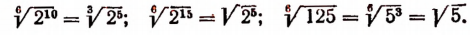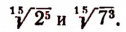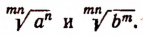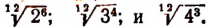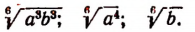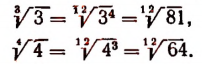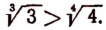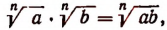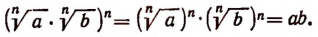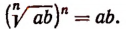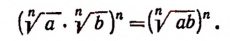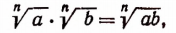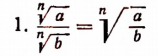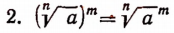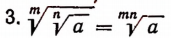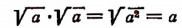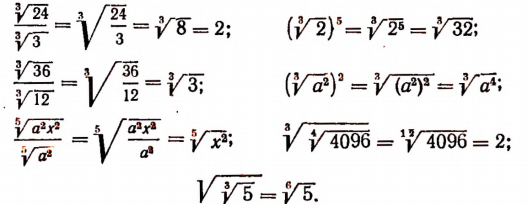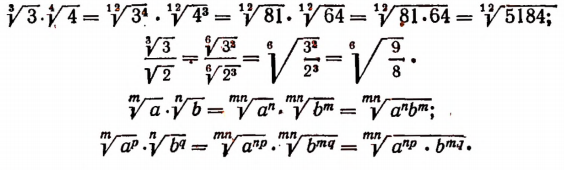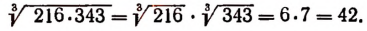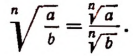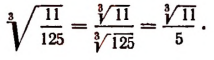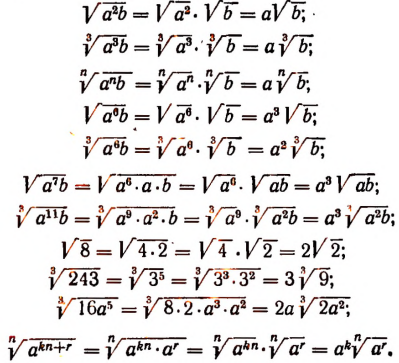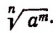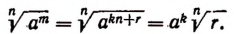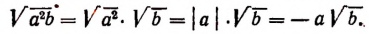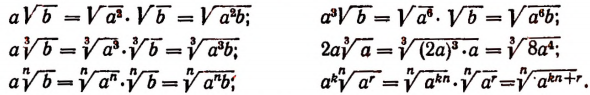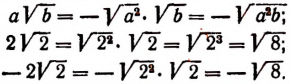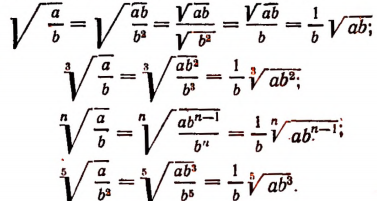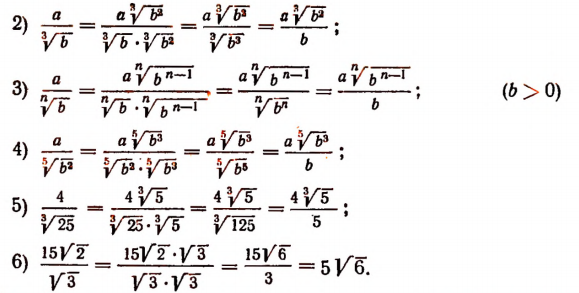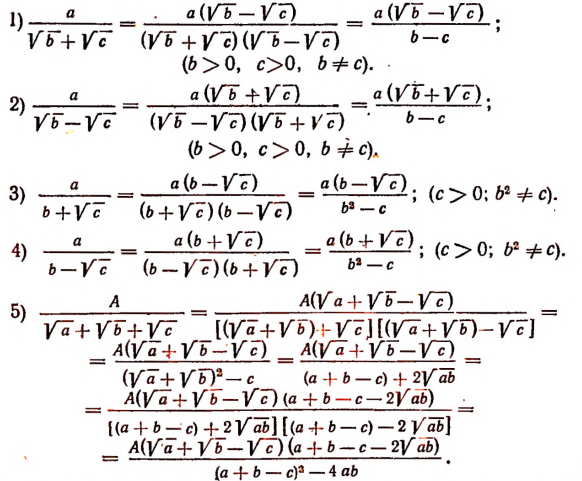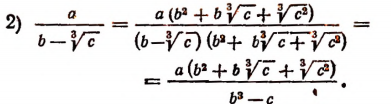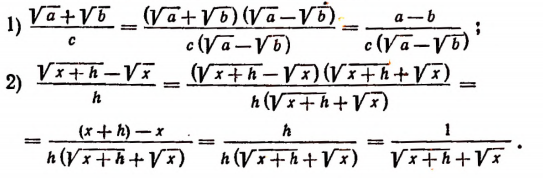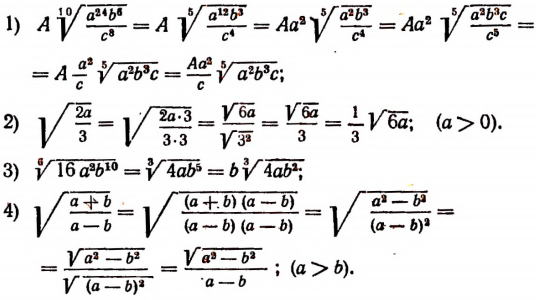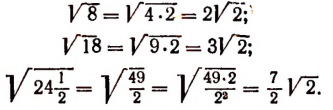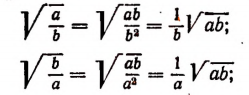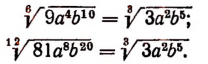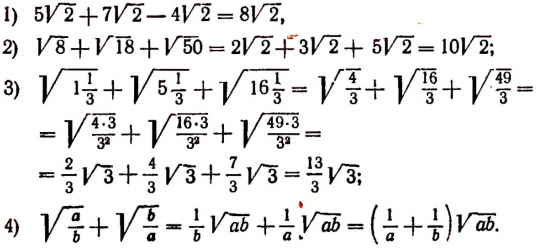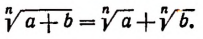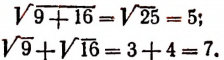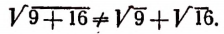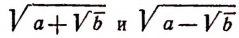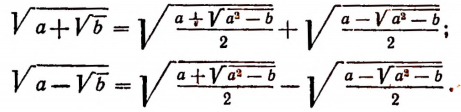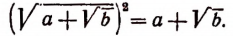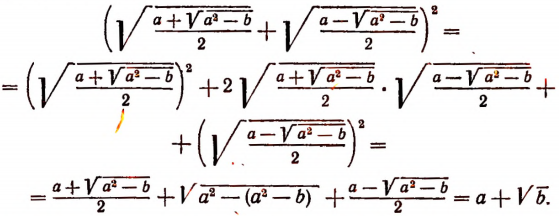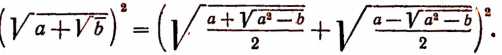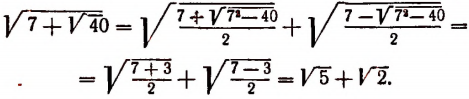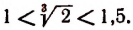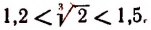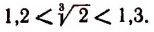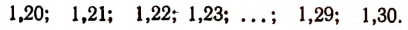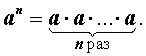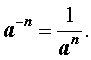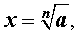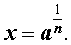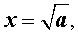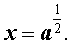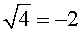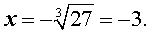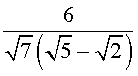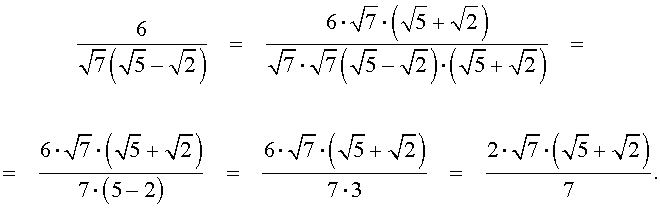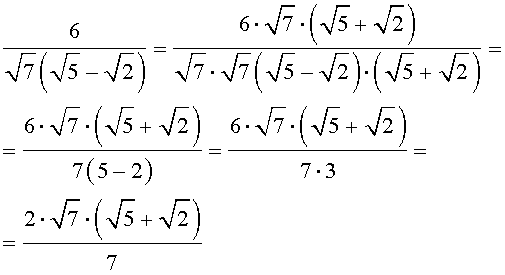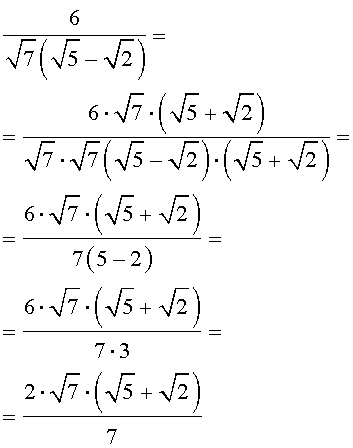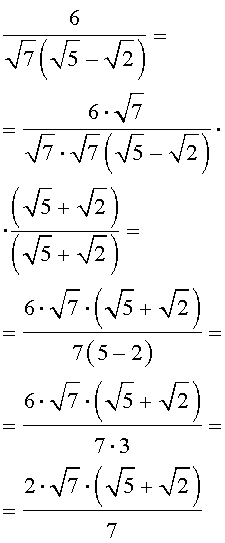Арифметический корень n-й степени
Арифметический корень натуральной степени
Арифметическим корнем натуральной степени $n \ge 2$ из неотрицательного числа $a \ge 0$ называется неотрицательное число, n-я степень которого равна a.
Поиск корня n-й степени называют извлечением корня n-й степени.
Эта операция является обратной возведению в n-ю степень.
$ \sqrt[3] <27>= 3, т.к. 3^3 = 27 $
$ \sqrt[4] <625>= 5, т.к. 5^4 = 625 $
Корень нечётной степени из отрицательного числа
Если степень n нечётная, то корнем нечётной степени n из отрицательного числа $a \lt 0$ называют такое отрицательное число, n-я степень которого равна a.
Решение уравнений $x^n = a$
$$ x^2 = 16 \iff x^2-16 = 0 \iff (x+4)(x-4) = 0 \iff \left[ \begin
$$ x^2 = -9 \lt 0 \iff x \in \varnothing, решений \quad нет$$
$$ x^4 = 81 \iff x^4-81 = 0 \iff (x^2+9)(x^2-9) = 0 \iff $$
$$ \iff (x^2+9)(x+3)(x-3) = 0 \iff \left[ \begin
$$ x^3 = 27 \iff x^3-27 = 0 \iff (x-3)(x^2+3x+9) = 0 \iff x = 3 $$
$$ x^3 = -27 \iff x^3+27 = 0 \iff (x+3)(x^2-3x+9) = 0 \iff x = -3 $$
Если n – чётно и $a \ge 0$, уравнение $x^n = a$ имеет два решения: $x = \pm \sqrt[n]$
Если n – чётно и $a \lt 0$, уравнение $x^n = a$ решений не имеет.
Если n — нечётно, уравнение $x^n = a$ имеет одно решение $x = \sqrt[n]$ при любом $a \in \Bbb R$.
Свойства арифметических корней натуральной степени
$$ \sqrt[n]
Примеры
Пример 1. Упростите выражение:
Пример 2. Вычислите:
Пример 3. Сравните числа:
$ 14 \lt 17 \Rightarrow \sqrt[3] <14>\lt \sqrt[3] <17>$
$ -14 \gt -17 \Rightarrow \sqrt[3] <-14>\gt \sqrt[3] <-17>$
$ \sqrt[3] <-14>\lt 0 \lt \sqrt <5>\Rightarrow \sqrt[3] <-14>\lt \sqrt <5>$
$ \sqrt[3] <29>\gt \sqrt[3] <27>= 3, \sqrt[4] <78>\lt \sqrt[4] <81>= 3 $
$ \sqrt[4] <78>\lt 3 \lt \sqrt[3] <29>\Rightarrow \sqrt[3] <29>\gt \sqrt[4] <78>$
Пример 4. Найдите область определения функции:
Выражение под чётным корнем должно быть неотрицательным:
$ \frac
Область определения: $x \in (-\infty;-3] \cup (1;+\infty)$
Выражение под нечётным корнем может иметь любой знак.
Ограничения области определения связаны только с делением на 0:
Область определения: $x \in (-\infty;-3) \cup (-3;8) \cup (8;+\infty)$
Пример 5. Решите уравнение:
$ x = \pm \sqrt[6] <64>= \pm \sqrt[6] <2^6>= \pm 2 $
$ x \in \varnothing$ — решений нет
Пример 6*. Найдите значение выражения $\sqrt[3]<9+\sqrt<80>> +\sqrt[3]<9-\sqrt<80>>$
Мы получили уравнение: $A^3 = 3(A+6)$ или $ \frac
Арифметические корни в математике с примерами решения и образцами выполнения
Если а есть положительное рациональное число, представляющее собой точный квадрат, то арифметический квадратный корень из него есть положительное рациональное число. Например:
Если положительное рациональное число Q не представляет собой точного квадрата, то арифметический квадратный корень из него есть положительное иррациональное число. Например:
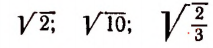
Сказанное относительно арифметического квадратного корня распространяется соответствующим образом на кубические корни и на корни любой степени. Например:
Корни 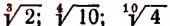
Действительные корни нечетных степеней из отрицательного числа суть числа отрицательные. Например:
Действительных корней четной степени из отрицательных чисел не существует.
Например, не существует такого действительного числа q, чтобы равенство
В самом деле, 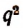
Поэтому 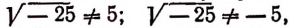
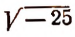
Арифметические корни из степеней
Правило. Если подкоренное выражение представляет степень положительного числа а и при этом показатель этой степени делится на показатель корня, то арифметический корень будет равен степени, основанием которой служит а, а показателем — частное от деления показателя степени, стоящей под корнем, на показатель корня.
Примеры:
О выражении
Если а > 0, то
Если же а
Например,
О выражении
Из определения следует, что
Подставляя вместо q равное ему выражение 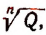
что и требовалось доказать.
Примеры:
Основное свойство арифметического корня
Вспомогательные предложения
Прежде чем формулировать и доказывать основное свойство арифметического корня, докажем несколько вспомогательных предложений.
Определение:
Если М и N два различных действительных числа, то М> N, если разность М— N есть число положительное.
Доказательство:
Разность Am — Вm можно записать в виде
По условию А — В > 0 и m > 0, следовательно, разность Am — Вm есть число положительное, а это и значит, что Am > Вm. Как раз это и требовалось доказать.
Предложение 2-е.
Если а > b и с > d и при этом все числа а, b, с, d положительные, то
Доказательство:
Из того, что а > b и с > 0 следует ас > bc. Из того, что
с > d и b > О следует bc > bd. Из того, что ас>bс и bc>bd следует, что ac>bd, что и требовалось доказать.
Предложение 3-е.
Если х > у и при этом числа х, у— положительные, то 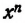
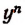
Доказательство:
Из того, что х > у и х>0 следует
Из того, что х > у и у > 0 следует
Из того, что 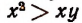
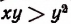
Продолжая аналогичные рассуждения, получим:
что и требовалось доказать.
Предложение 4-е.
Если 
Доказательство. Предположим, что х> у, тогда 
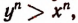
Примечание:
Из равенства 
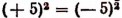
Формулировка основного свойства арифметического корня
Арифметическое значение корня не изменится, если показатель корня умножить на натуральное число, а подкоренное выражение возвысить в степень этого же натурального числа, т. е.
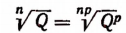
Доказательство:
Очевидно, что 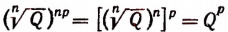
Две величины, порознь равные третьей, равны между собой. Поэтому
Но так как числа 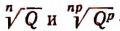
что и требовалось доказать.
Примеры:
Основное свойство арифметического корня позволяет нам сокращать показатель корня в тех случаях, когда это возможно.
Примеры:
Основное свойство арифметического корня позволяет нам приводить к общему показателю корни, имеющие разные показатели.
Примеры:
Корни 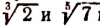
Корни 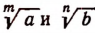
Корни 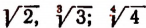
Корни 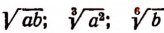
Чтобы определить, какое из двух чисел, например, 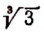
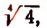
Ясно, что
Действия над арифметическими корнями
Умножение
Произведение корней, имеющих одинаковые показатели, равно корню с тем же показателем из произведения подкоренных выражений перемножаемых корней, т. е.
(n — число натуральное, а и b — числа положительные).
Доказательство:
Tакже очевидно, что
Две величины, порознь равные третьей, равны между собой. Поэтому
Но так как числа 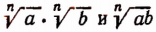
что и требовалось доказать.
Совершенно аналогичным путем можно доказать правила для других действий.
Другие действия
(Правило деления корней, имеющих одинаковые показатели.)
(Правило возведения корня в степень.)
(Правило извлечения корня из корня.)
Учащемуся предлагается самостоятельно сформулировать и доказать каждое из трех последних правил.
Примечание:
Обратим внимание на то, что равенство
справедливо лишь при условии, что а > 0. (При 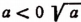
Примеры:
Правило. Чтобы перемножить или разделить корни, имеющие разные показатели, необходимо привести эти корни предварительно к общему показателю.
Примеры:
Запишем равенство 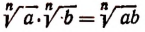
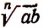
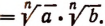
Пример:
Пример:
Некоторые важные преобразования
Вывод множителей из-под знака корня
Пусть а и b — положительные числа. Тогда
Пусть при делении числа m на n получается в частном k, а в остатке r. Тогда 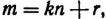
Пусть a — отрицательное число, а b — положительное. Тогда
Итак, если подкоренное выражение разлагается на такие множители, что из некоторых можно извлечь точный корень, то такие множители по извлечении из них корня могут быть выведены из-под знака корня в качестве множителей.
Введение под знак корня
Пусть а и b — положительные числа. Тогда
Пусть а — отрицательное число, а b — положительное. Тогда
Преобразование корня из дроби к корню из целого выражения
Пусть а и b — положительные числа. Тогда
Устранение иррациональности в знаменателе дроби
Устранить иррациональность в знаменателе дроби — это значит преобразовать дробь, знаменатель которой содержит корни, к новой дроби, знаменатель которой корней не содержит.
Мы рассмотрим лишь некоторые частные случаи такого преобразования.
а) Случай, когда знаменатель есть корень.
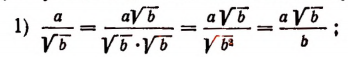
б) Случай, когда знаменатель есть сумма или разность, содержащая квадратные корни.
в) Случай, когда знаменатель есть сумма или разность, содержащая кубические корни.
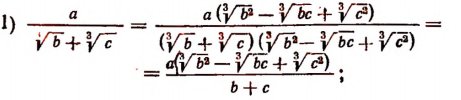
Устранение иррациональности в числителе дроби
Устранить иррациональность в числителе дроби — это значит преобразовать дробь, числитель которой содержит корни, к новой дроби, числитель которой корней не содержат.
Эта операция производится аналогично тому, как и операции, указанные в предыдущем пункте. Например:
Нормальный вид корня
Корень считается приведенным к нормальному виду, если:
1) возможные множители вынесены за знак корня;
2) подкоренное выражение приведено к целому виду;
3) показатель корня и показатель степени подкоренного выражения сделаны взаимно простыми.
Примеры:
Подобные корни и их приведение
Корни называются подобными, если после приведения их к нормальному виду окажутся одинаковыми как их подкоренные выражения, так и показатели корней.
Примеры:
Корни 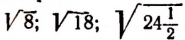
Действительно,
Корни 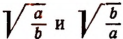
Корни 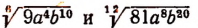
Приведение подобных корней
Примеры:
При извлечении корня из суммы нельзя производить извлечение корней из слагаемых, т. е. нельзя писать
Отсюда видно, что
Преобразование сложного корня
называются сложными корнями.
Теорема:
Если а > 0, b > 0 и 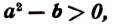
Докажем справедливость первой формулы. Очевидно, что
С другой стороны,
Две величины, порознь равные третьей, равны между собой. Поэтому
Основания этих квадратов положительны, а поэтому
что и требовалось доказать.
Совершенно так же доказывается и вторая формула.
Доказанные формулы представляют особый интерес в том случае, когда разность 
Замечание:
Корни иногда называют радикалами.
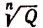
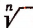
Общее определение корня
Корнем n-й степени из числа а называется всякое число х, n-я степень которого равна а.
Правило нахождения всех значений корня n-й степени из любого числа изложено в гл. «Комплексные числа».
В настоящей главе мы изучали лишь арифметические значения корней.
О возможности нахождения арифметического корня с любой степенью точности
Мы покажем сейчас, что элементарным способом можно находить значение любого арифметического корня с любой степенью точности. Сущность этого способа раскроем на примере хотя бы
Пусть требуется найти 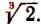
Очевидно, что 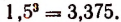
Далее 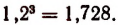
Наконец, 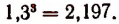
Теперь можно сказать, что 1,2 будет приближенным значением 
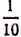
Чтобы получить приближенные значения с точностью до 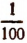
Этот процесс можно продолжить как угодно далеко и таким путем получить значение 
Изложенный элементарный способ имеет принципиальное значение, но не практическое. Практически пользоваться этим способом крайне неудобно, так как он слишком громоздок. Принципиальное же значение этого способа заключается в том, что он убеждает нас в возможности отыскания значений любого арифметического корня с любой степенью точности.
Для практического же вычисления значений любых арифметических корней существуют другие более удобные способы. Один из этих способов мы встретим в главе «Логарифмы».
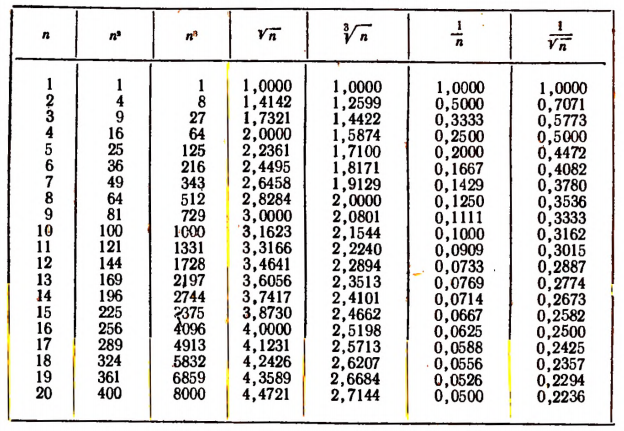
Для нахождения приближенных значений часто встречающихся величин можно пользоваться готовыми таблицами. Пример подобной таблицы приведен ниже.
Таблица квадратов, кубов, корней квадратных, корней кубических и обратных величин
Такого рода таблицы, значительно более полные и с более высокой степенью точности, даны, например, в книге Барлоу: «Таблицы квадратов, кубов, корней квадратных, корней кубических и обратных величин».
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Степень с целочисленным показателем и арифметический корень
 Степень с целочисленным показателем Степень с целочисленным показателем |
 Арифметический корень Арифметический корень |
 Избавление от иррациональностей в знаменателе дроби Избавление от иррациональностей в знаменателе дроби |
Степень с целочисленным показателем
Понятие степени с целочисленным показателем включает в себя три определения.
Определение . Пусть n – произвольное натуральное число, а a – произвольное действительное число. Тогда n – ой степенью числа a называют произведение n сомножителей, равных a :
Число a называют основанием степени , а число n – показателем степени .
Определение . Пусть a – произвольное действительное число, отличное от 0 . Тогда, по определению:
Число a называют основанием степени , а число 0 – показателем степени .
Определение . Пусть n – произвольное натуральное число, а a – произвольное действительное число, отличное от 0 . Тогда, по определению:
Число a называют основанием степени , а число (– n) – показателем степени .
Таким образом, степень с целочисленным показателем определена.
Замечание 1 . Число нуль нельзя возвести в нулевую степень и нельзя возвести в отрицательную степень.
Арифметический корень
Пусть n – произвольное натуральное число, а a – произвольное положительное число.
Определение . Число x называют арифметическим корнем n – ой степени из числа a , если, во-первых, число x положительное, а, во-вторых, является решением уравнения
В этом случае при 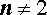
или эквивалентное обозначение:
Если же n = 2 , то для арифметического квадратного корня используется обозначение:
или эквивалентное обозначение:
Замечание 2 . В курсах математики, выходящих за рамки средней школы, доказывается, что арифметический корень всегда существует, причем только один.
Замечание 3 . Очень важно помнить о том, что в формуле
содержится ошибка, за которую мгновенно следует безжалостная кара на экзаменах.
Пример 2 . Решить уравнение
Решение . Это уравнение имеет два корня:
Корень уравнения x1 = 5 является арифметическим квадратным корнем из числа 25 , а корень уравнения x2 = – 5 является числом, противоположным к арифметическому квадратному корню из числа 25 .
Пример 3 . Решить уравнение
Решение . Это уравнение имеет единственный вещественный корень x = – 3 , но это число не является арифметическим кубическим корнем из числа (– 27), так как у отрицательных чисел не бывает арифметических корней. Число x = – 3 является числом, противоположным к арифметическому кубическому корню из числа 27 . Поэтому
Замечание 4 . Желающие могут ознакомиться с нашей презентацией «Степень с рациональным показателем», содержание которой связано с данным разделом.
Избавление от иррациональностей в знаменателе дроби
В некоторых задачах требуется перейти от дроби к равной ей дроби, но такой, у которой в знаменателе нет корней (иррациональностей). Эта операция носит название «избавление от иррациональностей в знаменателе дроби» и осуществляется при помощи умножения числителя и знаменателя дроби на подходящее число. Часто это число находится с помощью формул сокращенного умножения. Покажем это на примере.
Пример 4 . Преобразовать дробь
к такому виду, чтобы в знаменателе не было иррациональностей.
Решение . Воспользовавшись формулой сокращенного умножения «Разность квадратов», совершим следующие эквивалентные преобразования:
Мы получили дробь, у которой в знаменателе иррациональностей нет, что и требовалось.
С понятием степени с рациональным показателем и свойствами степеней можно ознакомиться в разделе «Степень с рациональным показателем» нашего справочника.
Графики степенных и показательных функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.
http://lfirmal.com/arifmeticheskie-korni/
http://www.resolventa.ru/spr/algebra/degree2.htm