Задания для самоподготовки по теме: «Системы линейных уравнений с двумя неизвестными» 7 класс
план-конспект урока (алгебра, 7 класс) по теме
Скачать:
| Вложение | Размер |
|---|---|
| zadaniya_dlya_samopodgotovki_po_teme_sistemy_uravneniy_7_i_8klass.doc | 142.5 КБ |
Предварительный просмотр:
Задания для самоподготовки по теме: «Системы линейных уравнений с двумя неизвестными»
3х-2у=0. 3х+у=7. 5х+2у=0. 5х-2у=9.
5. х+5у=7, 6. х+у=7, 7. 4х-3у=-1, 8. х+2у=-2,
3х+2у=-5. 5х-7у=11. х-5у =4. 3х-у=8.
9. 2х-5у=-7, 10. х-у=3, 11. 3х-5у=16, 12. 2х+3у=-7,
х-3у=-5. 3х+4у=2. 2х+у=2. х-у=4.
13. 2х+5у=-7, 14. х-3у=8, 15. 2х-3у=5, 16. х-4у=-1,
3х-у=15. 2х-у=6. х-6у=-2. 3х-у=8.
17. 5х-4у=12, 18. 6х+у=5, 19. 2х-3у=11, 20. х-6у=-2,
х-5у=-6. 2х-3у=-5. 5х+у=2. 2х+3у=11.
21. 3х-2у=16, 22. 2х+3у=3, 23. 4х-2у=-6, 24. 3х+2у=8,
4х+у=3. 5х+6у=9. 6х+у==11. 2х+6у=10.
25. 5х+у==14, 26. 3х-2у=5, 27. х+4у=7, 28. 2х-3у=5,
3х-2у=-2. 2х+5у=16. х-2у=-5. 3х+2у=14.
29. х-2у=7, 30. 4х-6у=26, 31. х+3у=7, 32. 8х+3у=-21,
х+2у=-1. 5х+3у=1. х+2у=5. 4х+5у=-7.
33. х-2у=8, 34. 8х+2у=11, 35. 2х-у=13, 36. 7х+3у=1,
х-3у=6. 6х-4у=11. 2х+3у=9. 2х-6у=-10.
37. 2х+3у=10, 38. 3х-2у=5, 39. 2х+у=-5, 40. 2х+3у=1,
х-2у=-9. 5х+4у=1. х-3у=-6. 6х-2у=14.
Задания для самоподготовки по теме: «Системы уравнений второй степени с двумя неизвестными»
2х+у=6. ху=-14. 2ху=3. х 2 +2у=33.
5. 3ху=1, 6. у-х=2, 7. 4у-х=1, 8. х-у=1,
6х+у=3. 4х+у 2 =13. 2ху =1. х 2 -у=3.
9. х 2 -у=-2, 10 . х+у=4, 11. 3х-у=-10, 12. х+у=5,
2х+у=2. х 2 -у=2. х 2 +у=10. ху=6.
13. х-у=7, 14. ху=8, 15. х-у=7, 16. х+у=1,
ху=-10. х+у=6. ху=-12. х 2 +у 2 =25.
17. х+у=10, 18. х+у=3, 19. х-у=4, 20. 2х+у 2 =6,
х 2 -у 2 =40. х 2 +у 2 =29. х 2 -у 2 =40. х+у=3.
21. х-у=4, 22. х-у=2, 23. х-у=4, 24. х-у=6,
ху=5. 3х-у 2 =6. ху==12. х 2 +у 2 =20.
25. х 2 -3у==22, 26. х-у=4, 27. х+у=4, 28. х-у=2,
х+у=2. х 2 +у 2 =10. х 2 -4у=5. х-у 2 =2.
29. х+у=2, 30. х 2 -у=-1, 31. у-х=2, 32. х 2 +2у=12,
ху=-15. х+у=1. у 2 -4х=13. 2х-у=10.
33 . х 2 -3у=1, 34. х-2у=2, 35 . х-у=-6, 36. х+у=-2,
х+у=3. 3х-у 2 =11. ху=40. у 2 -3х=6.
37. х-у=4, 38. х 2 +ху=12, 39. 2х+у=-5, 40. 2х+3у=1,
ху+у 2 =6. у-х=2. х-3у=-6. 6х-2у=14.
41. х-у=5, 42. х+у=3, 43. у 2 -3ху+х 2 -х+у+9=0,
х 2 +2ху-у 2 =-7. х 2 +2ху+2у 2 =18. у-х=2.
47. х-у=7, 48. — =-2, 49. + =4,
Ответы к теме: ««Системы линейных уравнений с двумя неизвестными»
Ответы к теме: «Системы уравнений второй степени с двумя неизвестными»
По теме: методические разработки, презентации и конспекты
Двумерные массивы (прямоугольные таблицы). Информационная модель решения системы линейных уравнений с двумя неизвестными методом Крамера.
На уроке мы изучаем метод Крамера для решения системы линейных уравнений, основанный на вычислении определителя прямоугольной матрицы, и составляем информационную модель вычисления корней с испо.
Презентации к урокам алгебры в 7 классе по теме «Системы линейных уравнений с двумя неизвестными».
Презентации сделаны к урокам алгебры в 7 классе по теме «Системы линейных уравнений с двумя неизвестными». Эти презентации могут быть как частью урока, так и монтировать целый урок. Эти пр.
«Системы линейных уравнений с двумя неизвестными»
Презентация по алгебре 7 класса содержит определение системы линейных уравнений , понятие решения системы линейных уравнений.Рассмотрены возможные случаи существования решений системы уравнений.
Презентация Системы линейных уравнений с двумя неизвестными.
Знакомство со способами решения систем линейных уравнений с двумя неизвестными.
Конспект урока 7 класс » «РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ МЕТОДОМ ПОДСТАНОВКИ»
Представлен конспект урока изучения нового материала по теме «РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ МЕТОДОМ ПОДСТАНОВКИ».
Урок алгебры в 7 классе по теме «Системы линейных уравнений с двумя неизвестными».
Урок закрепления темы «Системы линейных уравнений с двумя неизвестными» — 10 урок в теме. На уроке применяются коллективная, групповая, индивидуальная, дифференцированная формы работы.
Урок алгебры в 7 классе по теме «Системы линейных уравнений с двумя неизвестными»
Урок закрепления темы «Системы линейных уравнений с двумя неизвестными» — 10 урок в теме. На уроке применяются коллективная, групповая, индивидуальная, дифференцированная формы работы.
Уравнения с двумя переменными (неопределенные уравнения)
Разделы: Математика
Обращение автора к данной теме не является случайным. Уравнения с двумя переменными впервые встречаются в курсе 7-го класса. Одно уравнение с двумя переменными имеет бесконечное множество решений. Это наглядно демонстрирует график линейной функции, заданный в виде ax + by=c. В школьном курсе учащиеся изучают системы двух уравнений с двумя переменными. В результате из поля зрения учителя и, поэтому ученика, выпадает целый ряд задач, с ограниченными условиями на коэффициент уравнения, а также методы их решения.
Речь идет о решении уравнения с двумя неизвестными в целых или натуральных числах.
В школе натуральные и целые числа изучаются в 4-6-х классах. К моменту окончания школы не все ученики помнят различия между множествами этих чисел.
Однако задача типа “решить уравнение вида ax + by=c в целых числах” все чаще встречается на вступительных экзаменах в ВУЗы и в материалах ЕГЭ.
Решение неопределенных уравнений развивает логическое мышление, сообразительность, внимание анализировать.
Я предлагаю разработку нескольких уроков по данной теме. У меня нет однозначных рекомендаций по срокам проведения этих уроков. Отдельные элементы можно использовать и в 7-м классе (для сильного класса). Данные уроки можно взять за основу и разработать небольшой элективный курс по предпрофильной подготовке в 9-м классе. И, конечно, этот материал можно использовать в 10-11 классах для подготовки к экзаменам.
Цель урока:
- повторение и обобщение знаний по теме “Уравнения первого и второго порядка”
- воспитание познавательного интереса к учебному предмету
- формирование умений анализировать, проводить обобщения, переносить знания в новую ситуацию
Урок 1.
Ход урока.
1) Орг. момент.
2) Актуализация опорных знаний.
Определение. Линейным уравнением с двумя переменными называется уравнение вида
mx + ny = k, где m, n, k – числа, x, y – переменные.
Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.
1. 5x+2y=12 
Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.
Пусть x = 2, y = -2.5•2+6 = 1
x = 4, y = -2.5•4+6 =- 4
Пары чисел (2;1); (4;-4) – решения уравнения (1).
Данное уравнение имеет бесконечно много решений.
3) Историческая справка
Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.
В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.
Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.
4) Изучение нового материала.
Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y 

Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Пример: 34x – 17y = 3.
НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет.
Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно простыми.
Если m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.
Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений:




Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)
m, n, x, y 
Если m и n – взаимно простые числа, то всякое решение уравнения (2) имеет вид
5) Домашнее задание. Решить уравнение в целых числах:
Замечание. На данном уроке не представлены примеры решения уравнений в целых числах. Поэтому домашнее задание дети решают исходя из утверждения 1 и подбором.
Урок 2.
1) Организационный момент
2) Проверка домашнего задания
5 не делится нацело на 9, в целых числах решений нет.
Методом подбора можно найти решение
3) Составим уравнение:
Пусть мальчиков x, x 

Многие учащиеся, составив уравнение, не смогут его решить.
Ответ: мальчиков 4, девочек 6.
3) Изучение нового материала
Столкнувшись с трудностями при выполнении домашнего задания, учащиеся убедились в необходимости изучения их методов решений неопределенных уравнений. Рассмотрим некоторые из них.
I. Метод рассмотрения остатков от деления.
Пример. Решить уравнение в целых числах 3x – 4y = 1.
Левая часть уравнения делится на 3, следовательно, должна делиться и правая часть. Рассмотрим три случая.
- Если y = 3m, m
Z, то 4y + 1= 4•3m + 1 = 12m + 1 не делится на 3.
- Если y = 3 m + 1, то 4y +1 = 4• (3m + 1)+1 = 12m + 5 не делится на 3.
- Если y = 3 m + 2, то 4y +1 = 4• (3m + 2)+1 = 12m + 9 делится на 3, поэтому 3x = 12m + 9, следовательно, x = 4m + 3, а y = 3m + 2.
Ответ: 

Описанный метод удобно применять в случае, если числа m и n не малы, но зато разлагаются на простые сомножители.
Пример: Решить уравнения в целых числах.
Пусть y = 4n, тогда 16 — 7y = 16 – 7•4n = 16 – 28n = 4*(4-7n) делится на 4.
y = 4n+1, тогда 16 – 7y = 16 – 7• (4n + 1) = 16 – 28n – 7 = 9 – 28n не делится на 4.
y = 4n+2, тогда 16 – 7y = 16 – 7• (4n + 2) = 16 – 28n – 14 = 2 – 28n не делится на 4.
y = 4n+3, тогда 16 – 7y = 16 – 7• (4n + 3) = 16 – 28n – 21 = -5 – 28n не делится на 4.
Следовательно, y = 4n, тогда
4x = 16 – 7•4n = 16 – 28n, x = 4 – 7n
Ответ: 

II. Неопределенные уравнения 2-ой степени
Сегодня на уроке мы лишь коснемся решения диофантовых уравнений второго порядка.
И из всех типов уравнений рассмотрим случай, когда можно применить формулу разности квадратов или другой способ разложения на множители.
Пример: Решить уравнение в целых числах.
13 – простое число, поэтому оно может быть разложено на множители лишь четырьмя способами: 13 = 13•1 = 1•13 = (-1)(-13) = (-13)(-1)
Рассмотрим эти случаи
а) 
б) 
в) 
г) 
4) Домашнее задание.
Примеры. Решить уравнение в целых числах:
а)
 |  |  |
| 2x = 4 | 2x = 5 | 2x = 5 |
| x = 2 | x = 5/2 | x = 5/2 |
| y = 0 | не подходит | не подходит |
 |  |  |
| 2x = -4 | не подходит | не подходит |
| x = -2 | ||
| y = 0 |
б)
в)
Итоги. Что значит решить уравнение в целых числах?
Какие методы решения неопределенных уравнений вы знаете?
Упражнения для тренировки.
1) Решите в целых числах.
| а) 8x + 12y = 32 | x = 1 + 3n, y = 2 — 2n, n  Z Z |
| б) 7x + 5y = 29 | x = 2 + 5n, y = 3 – 7n, n  Z Z |
| в) 4x + 7y = 75 | x = 3 + 7n, y = 9 – 4n, n  Z Z |
| г) 9x – 2y = 1 | x = 1 – 2m, y = 4 + 9m, m  Z Z |
| д) 9x – 11y = 36 | x = 4 + 11n, y = 9n, n  Z Z |
| е) 7x – 4y = 29 | x = 3 + 4n, y = -2 + 7n, n  Z Z |
| ж) 19x – 5y = 119 | x = 1 + 5p, y = -20 + 19p, p  Z Z |
| з) 28x – 40y = 60 | x = 45 + 10t, y = 30 + 7t, t  Z Z |
2) Найти целые неотрицательные решения уравнения:
| а) 8x + 65y = 81 | x = 2, y = 1 |
| б) 17x + 23y = 183 | x = 4, y = 5 |
3) Найти все пары целых чисел (x; y), удовлетворяющие следующим условиям
| а) x + y = xy | (0;0), (2;2) |
б)  | (1;2), (5;2), (-1;-1), (-5;-2) |
Число 3 можно разложить на множители:
a)  | б)  | в)  | г)  |
в)  | (11;12), (-11;-12), (-11;12), (11;-12) |
г)  | (24;23), (24;-23), (-24;-23), (-24;23) |
д)  | (48;0), (24;1), (24;-1) |
е)  | x = 3m; y = 2m, m Z Z |
| ж) y = 2x – 1 | x = m: y = 2m – 1, m  Z Z |
з)  | x = 2m; y = m; x = 2m; y = -m, m  Z Z |
и) | решений нет |
4) Решить уравнения в целых числах
 | (-3;-2), (-1;1), (0;4), (2;-2), (3;1), (5;4) |
| (x — 3)(xy + 5) = 5 | (-2;3), (2;-5), (4;0) |
| (y + 1)(xy – 1)=3 | (0;-4), (1;-2), (1;2) |
 | (-4;-1), (-2;1), (2;-1), (4;1) |
 | (-11;-12), (-11;12), (11;-12), (11;12) |
 | (-24;23), (-24;23), (24;-23), (24;23) |
5) Решить уравнения в целых числах.
а)  | (-1;0) |
б) | (5;0) |
в)  | (2;-1) |
г)  | (2; -1) |
Решение задач с использованием систем линейных уравнений с двумя переменными.
Данная разработка предназначена для учеников 7 класса, а также для тех, кто желает отработать навык решения задач. Теоретическая часть содержит примеры решения задач с использованием систем уравнений. В практической части представлено большое количество задач с тематическим разделением.
Просмотр содержимого документа
«Решение задач с использованием систем линейных уравнений с двумя переменными.»
Решение задач с использованием систем линейных уравнений с двумя переменными.
Переходим теперь к практическому применению систем линейных уравнений с двумя переменными. Часто бывает, что в задачах неизвестны два, а то и три-четыре компонента. И в этом случае обозначение какого-то одного компонента переменной не облегчает решение задачи. Тогда нужно ввести две или три переменные. Вот здесь нам как раз и понадобится система уравнений и способы её решения. Приведём пример с полным описанием.
Например, решить задачу. Лодка за 3 ч движения по течению и 4 ч против течения проходит 114 км. Найдите скорость лодки по течению и её скорость против течения, если за 6 ч движения против течения она проходит такой же путь, как за 5 ч по течению.
Решение. В задаче описывается движение по воде. А значит, должна быть собственная скорость лодки и скорость течения реки. Они нам и не известны, поэтому обозначим через 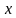
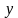

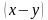
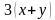
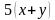
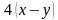

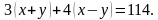
Для наглядности составим условие задачи в виде таблицы.
http://urok.1sept.ru/articles/417558
http://multiurok.ru/index.php/files/reshenie-zadach-s-ispolzovaniem-sistem-lineinykh-u.html