Формулы приведения. Примеры из ЕГЭ
Как вы, наверное, уже обратили внимание, формулы приведения разработаны для углов, представленных в одном из следующих видов: \(\frac<\pi><2>+a\), \(\frac<\pi><2>-a\), \(π+a\), \(π-a\), \(\frac<3\pi><2>+a\), \(\frac<3\pi><2>-a\), \(2π+a\) и \(2π-a\). Аналогично их можно использовать для углов представленных в градусах: \(90^°+a\), \(90^°-a\), \(180^°+a\), \(180^°-a\), \(270^°+a\), \(270^°-a\), \(180^°+a\), \(180^°-a\).
К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
Как быстро получить любую формулу приведения
Для начала обратите внимание, что все формулы имеют похожий вид:
Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс или котангенс , он либо останется синусом, либо превратиться в косинус . А котангенс никогда не станет синусом или косинусом, он либо останется котангенсом, либо станет тангенсом. И так далее.
Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
— как определить знак перед конечной функцией (плюс или минус)?
— как определить меняется ли функция на кофункцию или нет?
Как определить знак перед конечной функцией (плюс или минус)?
Какой знак был у исходной функции в исходной четверти, такой знак и нужно ставить перед конечной функцией.
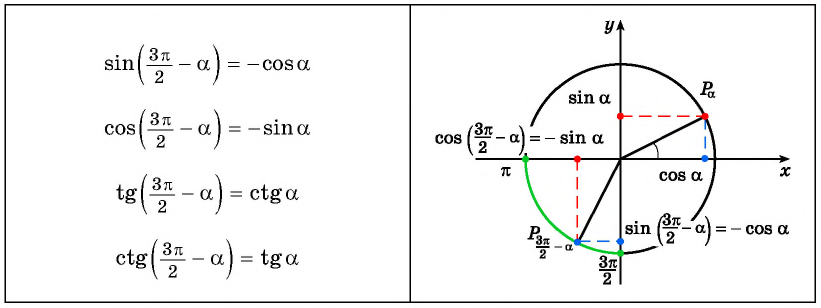
Например, выводим формулу приведения для \(cos(\frac<3\pi><2>-a) =. \) С исходной функцией понятно – косинус, а исходная четверт ь ?
Для того, чтобы ответить на этот вопрос, представим, что \(a\) – угол от \(0\) до \(\frac<\pi><2>\), т.е. лежит в пределах \(0°…90^°\) (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол \(\frac<3\pi><2>-a\)?
Чтобы ответить на вопрос, надо от точки, обозначающей \(\frac<3\pi><2>\), повернуть в отрицательную сторону на угол \(a\).
В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус. Поэтому перед итоговой функцией будет стоят минус: \(cos(\frac<3\pi><2>-a)=-. \)
Менять ли функцию на кофункцию или оставить прежней?
Здесь правило еще проще:
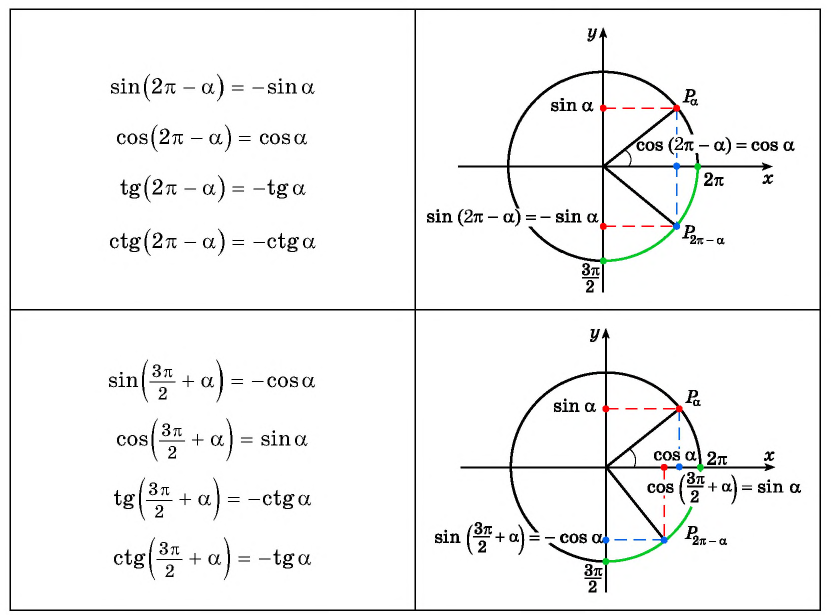
— если «точка привязки» \(\frac<\pi><2>\) (\(90^°\)) или \(\frac<3\pi><2>\) (\(270^°\))– функция меняется на кофункцию;
— если «точка привязки» \(π\) (\(180^°\)) или \(2π\) (\(360^°\)) – функция остается той же.
То есть, при аргументах исходной функции \(\frac<\pi><2>+a\), \(\frac<\pi><2>-a\), \(\frac<3\pi><2>+a\) или \(\frac<\pi><2>-a\), мы должны поменять функцию, а при аргументах \(π+a\), \(π-a\), \(2π+a\) или \(2π-a\) — нет. Для того, чтоб это легче запомнить, вы можете воспользоваться мнемоническим правилом, которое в школе называют «лошадиным правилом»:
Точки, обозначающие \(\frac<\pi><2>\) \((90^°)\) и \(\frac<3\pi><2>\) \((270^°)\), расположены вертикально, и если вы переводите взгляд с одной на другую и назад, вы киваете головой, как бы говоря «да».
Точки же, обозначающие \(π\) (\(180^°\)) и \(2π\) (\(360^°\)), расположены горизонтально, и если вы переводите взгляд между ними, вы мотаете головой, как бы говоря «нет».
Эти «да» и «нет» — и есть ответ на вопрос: «меняется ли функция?».
Таким образом, согласно правилу, в нашем примере выше \(\cos(\frac<3π><2>-a)=. \) косинус будет меняться на синус. В конечном итоге получаем, \(\cos(\frac<3π><2>-a)=-\sin\) \(a\). Это и есть верная формула приведения.
Примеры из ЕГЭ с формулами приведения:
Углы \(<41>^°\) и \(<49>^°\) нестандартные, поэтому «в лоб» без калькулятора вычислить непросто. Однако использовав формулы привидения, мы легко найдем правильный ответ.
Прежде всего, обратите внимание на один важный момент: \(49^°=90^°-41^°\). Поэтому мы можем заменить \(49^°\) на \(90^°-41^°\).
Теперь применим к синусу формулу приведения:
\(90^°-41^°\) – это первая четверть, синус в ней положителен. Значит, знак будет плюс;
\(90^°\)- находится на «вертикали» — функция меняется на кофункцию.
В числителе и знаменателе получились одинаковые косинусы. Сокращаем их.
Формулы приведения с примерами решения
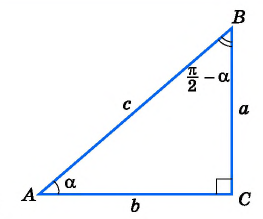
При изучении геометрии вы установили, что
если
Свойство периодичности тригонометрических функций позволяет свести вычисление значений синуса, косинуса, тангенса и котангенса произвольного угла к вычислению значений этих функций при значениях аргумента, принадлежащих промежутку 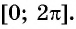
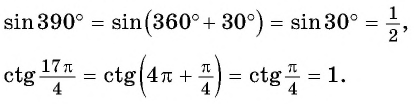
На практике принято сводить значения тригонометрических функций произвольного угла к вычислению значений этих функций для угла, принадлежащего промежутку 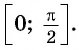
Это можно делать с помощью формул приведения.
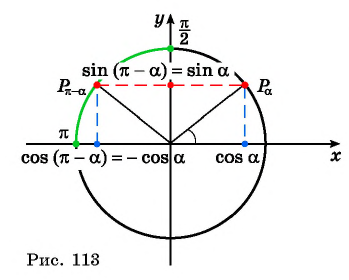
Рассмотрим промежуток 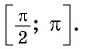
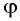
Например, 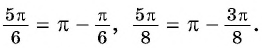
Поскольку ординаты точек 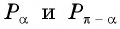
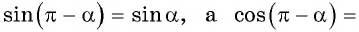
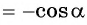
Тогда для 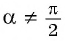
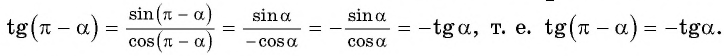
А для 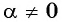
Вместе с тем любое число 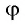
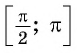
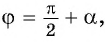
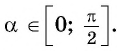
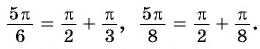
Так как ордината точки 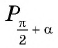
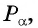
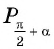
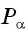
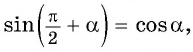
Для 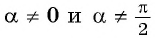
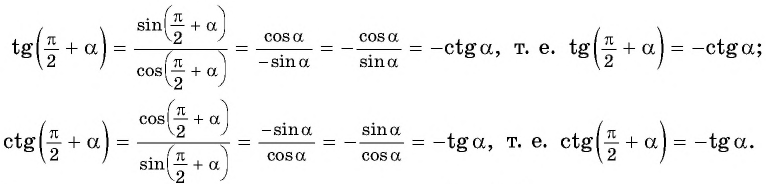
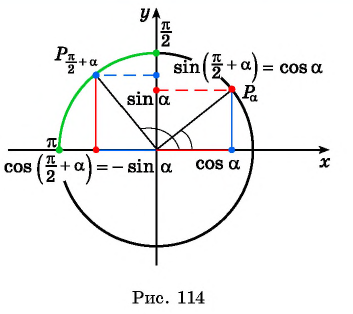
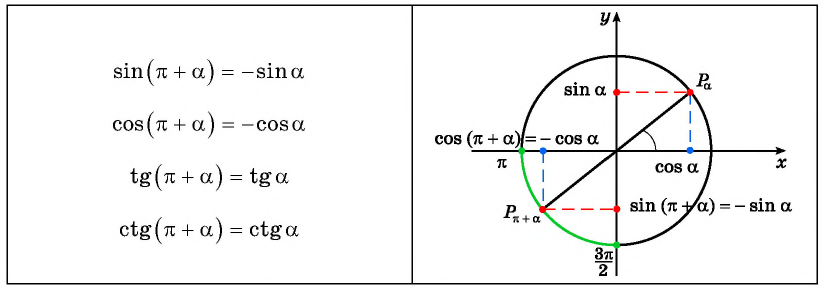
Так как любое число 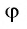
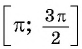
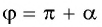
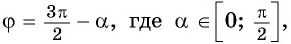
Поскольку любое число 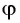
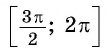
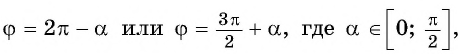
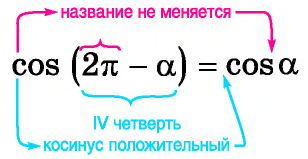
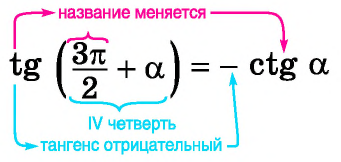
Проанализировав полученные формулы, можно заметить закономерности, позволяющие сформулировать правило, с помощью которого можно применять формулы приведения, не заучивая их:
В правой части формулы приведения ставится тот знак, который имеет в соответствующей четверти исходная функция, если считать, что угол 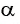
Если в формуле приведения аргумент имеет вид:
то название функции не меняется;
то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
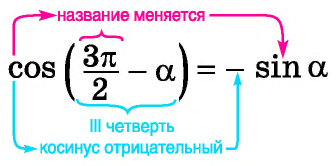
Например, применим полученное правило для выражения
- Если считать, что угол
— острый, то —
— угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».
- Поскольку аргумент имеет вид
то название функции «косинус» нужно поменять на «синус». Таким образом, получим:
Пример:
Приведите выражение к тригонометрической функции числа 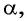
Решение:
а) 1. Так как 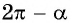
2. Поскольку аргумент имеет вид 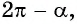
б) 1. Так как 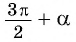
2.Поскольку аргумент имеет вид 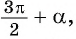
в) 1. Так как 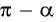
2. Поскольку аргумент имеет вид 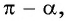
Пример:
Используйте формулы приведения и найдите значение выражения:
Решение:
Первый способ:
- Так как
угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».
- Поскольку аргумент имеет вид
то название функции «синус» не меняется. Значит,
Второй способ:
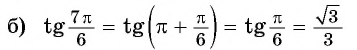
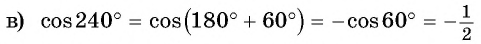
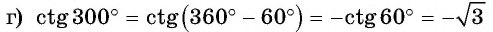
Пример:
Вычислите, используя формулы приведения:
Решение:
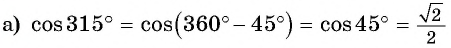
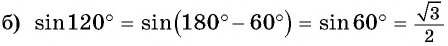

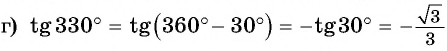
Пример:
Найдите значение выражения:
Решение:
а) Так как синус — нечетная функция, то
Применим формулы приведения:
б) Воспользуемся свойством четности косинуса и получим:
По формулам приведения:
в) Воспользуемся свойством периодичности тангенса и получим:
Применим формулы приведения:
г) Поскольку котангенс — нечетная функция, то
Используем свойство периодичности котангенса и получим:
Пример:
По формулам приведения:
Приведите к тригонометрической функции угла
Решение:
а) Используем свойство периодичности косинуса и получим:
По формулам приведения:
б) Воспользуемся свойством периодичности котангенса:
Применим формулы приведения:
в) Так как тангенс — нечетная функция, то 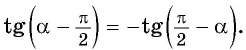
г) Поскольку синус — нечетная функция, то
Воспользуемся свойством периодичности синуса и получим:
По формулам приведения:
Пример:
Приведите к тригонометрической функции угла
Решение:
Пример:
Решение:
Пример:
Решение:
а) Применим формулы приведения:
б)Воспользуемся периодичностью косинуса и формулами приведения и получим:
в)Применим формулы приведения:
г) Используем периодичность тангенса, нечетность котангенса и формулы приведения:
Пример:
Решите уравнение:
Решение:
Применим формулы приведения и получим:
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Разработка урока в 10-м классе «Формулы приведения»
Разделы: Математика
- закрепить умение находить четверть и знак тригонометрических функций;
- закрепить умения использовать формулы сложения при упрощении тригонометрических выражений;
- вывести формулы приведения;
- выработать первичные навыки использования формул приведения;
- отработать алгоритм применения формул приведений;
- выполнить тест в качестве работы над ошибками по предыдущему материалу (для части учащихся).
- формировать умение работать группой;
- формировать умения делать логические заключения от частных случаев е общему выводу;
- умение работать с компьютером и проходить компьютерное тестирование;
- пользоваться умением самопроверки.
- интеллектуальное, эмоциональное, личностное развитие ученика;
- развивать умение обобщать, систематизировать на основе сравнения, делать вывод;
- активизация самостоятельной деятельности (деятельностный подход в обучении);
- развивать познавательный интерес;
- развивать наглядно-действенное творческое воображение.
Воспитательный аспект: способствовать формированию у учащихся чувства толерантности, стимулировать согласованное взаимодействие между учащимися, отношения взаимной ответственности и сотрудничества.
Воспитание коммуникативной и информационной культуры учащихся; умение учащихся данной группы построить на короткое время взаимодействия, исходя из особенностей задач.
Эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание на доске и в тетради, через наглядные и дидактические пособия.
Предполагаемые результаты обучающихся:
Знать: формулы приведения.
Уметь: определять четверть и знак тригонометрических функций; использовать формулы сложения при упрощении тригонометрических выражений.
Форма урока: практикум, с элементами исследования.
Форма организации обучения: фронтальная, индивидуальная, групповая.
Организация работы в группах на уроке преследует следующие цели:
- научить ребят самостоятельно и правильно распределять между собой роли при выполнении общих заданий и ответственно выполнять свои обязанности;
- научить ребят быть руководителями в групповой деятельности или исполнителями, т.е. подчиняться заданным правилам совместной работы;
- научить общаться друг с другом, устанавливать и поддерживать хорошие деловые взаимоотношения;
- научить ребят умело вести дискуссию, высказываться самим и слушать других, доказывать свою правоту и признавать правильность позиций других ребят.
Учащиеся рассажены за 4 стола (по 2 парты) группами по 6 человек в группе.
1. Организационный момент.
(введение в тему урока, формирование целей)
обращение внимания на написание слова “ПРИВЕДЕНИЯ”.
— Как вы понимаете это слово? Что значит формулы приведения? (делается вывод, что какое-то более сложное выражение будем приводить к определенному более простому виду)
— Формы нашей работы сегодня: устная работа на повторение, работа в группах (сразу назначить командиров групп и рассказать, что их обязанностью является распределение составляющих общего задания между членами группы). Для того чтобы успешно справиться с работой на уроке, нам необходим материал предыдущих занятий. И первое, что нам необходимо повторить, – это тригонометрический круг, значения синуса, косинуса, тангенса и котангенса различных углов.
Для проведения устной работы используется презентация (Приложение 1)
1 задание: Тригонометрический круг – тренажер. Точка-смайлик скользит по кругу, останавливаясь то на осях координат, то на различных точках круга. Учитель называет ученика и тот быстро называет значение точки (либо угол в радианах, либо значения синуса, косинуса, тангенса или котангенса на осях).
После выполнения этого задания двое учеников отправляются на последнюю парту проходить 5 -7 минутное проверочное интерактивное тестирование на ноутбуках по предыдущим темам: «Тригонометрический круг», «Основные тригонометрические тождества».
2 задание: Определить знак тригонометрических функций (Приложение 1):
Ответы на задание №2 «Определить знак тригонометрических функций»:
3 задание: Устно по слайдам:
Один ученик быстро выносит решение на доску.
— Итак, мы повторили формулы сложения, которые вам сегодня еще понадобятся.
А сейчас я вам хочу зачитать одну притчу:
«Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному дверному замку. «Кто откроет, тот и будет первым помощником». Никто не притронулся даже к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ. Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, но надеешься на собственные силы и не боишься сделать попытку».
— Сейчас каждой группе предстоит сделать попытку добыть новые знания, используя предыдущий опыт, предыдущие знания. Каждой группе дается задание заполнить таблицу, используя формулы сложения. Командир разбивает задание на составляющие части и распределяет между членами группы. Работать можно прямо в тетрадях. Конечные результаты заносятся в общую таблицу, которая у вас на столе. Н сером поле – «четверть» нужно проставить номер той четверти, куда попадает ваша исходная функция. Когда группа заполнит таблицу полностью, кто-либо из группы выносит результаты на доску. Все расчеты можно выполнять прямо в тетради. Объединив результаты работы 4-х групп, вы сами откроете и сформулируете новое правило (Дается время, на доске заготовлены 4 таблицы).
Таблица 1 группе:
Таблица 2 группе:
Таблица 3 группе:
Таблица 4 группе:
(Учителю в это время проверяет тесты, выполненные учащимися индивидуально на ноутбуках)
Вопросы группам после заполнения таблицы на доске:
- Что произошло с названием функции, поменялась ли функция?
- Какой знак стоит перед функцией в правой полученной части?
- Попробуйте найти закономерность между получившимся знаком перед функцией и номером четверти, которая на сером поле.
(Группы отвечают на вопросы. Ответы фиксируются учителем).
— У первой и второй группы названия функции поменялись, а у 3 и 4 групп остались прежними. Обратите внимание на углы, через которые вы приводили к углу 1 четверти: углы 

— Итак, мы прослушали ответы всех групп и вывели 32 формулы. Это и есть формулы приведения. Мы приводим к функции угла 1 четверти. Сможете ли вы их запомнить? И не нужно их запоминать механически. Давайте попробуем сделать общий вывод по результатам работы всех групп и сформулируем мнемоническое правило, которое позволит вам в дальнейшем самим быстро написать все формулы, которые будут необходимо. Ключевые моменты: название функции, знак функции. Я начинаю предложение, а вы продолжаете:
- Если приведение к углу
выполняется через вертикальные «рабочие» углы
название…. (функции меняется на конфункцию, синус на косинус, тангенс на котангенс и наоборот).
- Если приведение к углу
выполняется через горизонтальные «спящие» углы», то (название функции не меняется).
- В правой части формулы ставится тот знак, ….. (который имеет функция левой части) или – знак правой части определяется по знаку функции в правой части.
Смотрим на слайд и записываем правило в тетрадь в виде таблицы (Приложение 1)
— Где же применяются формулы приведения? Одно из применений — нахождение значений тригонометрических функций различных углов с помощью приведения к углу 1-ой четверти.
I способ:
II способ:
Решение упражнений с комментированием учащихся с места:
Второе применение – упрощение тригонометрических выражений – стр. 209, № 667(1) (выполняет ученик на доске с объяснением). При наличии времени №668 (2).
Домашнее задание: правило № 665 (весь), № 666 (четные) № 667 (2) 668(1)
3. Итог урока: Объявить результаты тестирования.
— Что вы сегодня узнали? (Как привести к функции угла 1 четверти)
Кто сможет повторить правило?
Но, а самый главный итог не в том, что вы узнали новое правило, а в том, что вы его вывели и получили самостоятельно. Помните притчу, которую я прочитала вам в начале урока? Так вот, главный итог в том, что вы полагались не только на то, что видели и слышали от меня, но надеялись на собственные силы и не боялись сделать попытку и получить результат самостоятельно и поэтому все замки сегодня для вас оказались открытыми.
http://www.evkova.org/formulyi-privedeniya
http://urok.1sept.ru/articles/503871





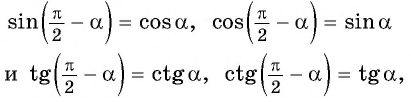
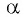
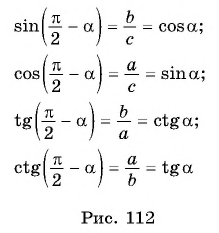
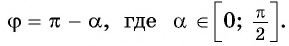
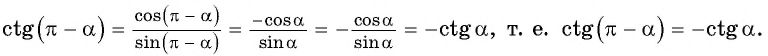
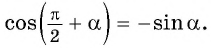
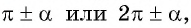 то название функции не меняется;
то название функции не меняется;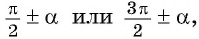 то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).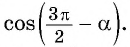
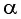 — острый, то —
— острый, то — 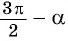 — угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».
— угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».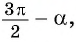 то название функции «косинус» нужно поменять на «синус». Таким образом, получим:
то название функции «косинус» нужно поменять на «синус». Таким образом, получим: 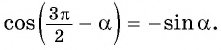
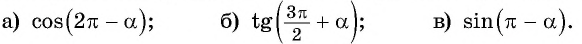
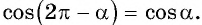
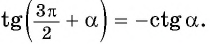
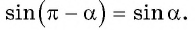

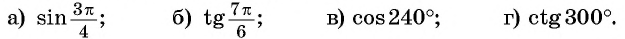
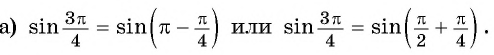
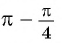 угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».
угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».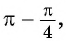 то название функции «синус» не меняется. Значит,
то название функции «синус» не меняется. Значит, 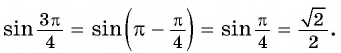


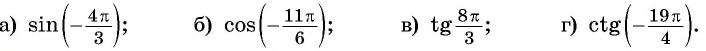
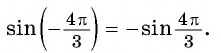
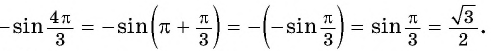
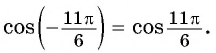
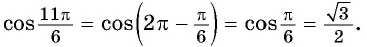
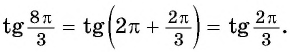
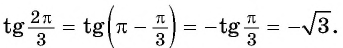
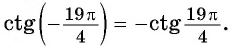
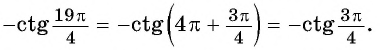
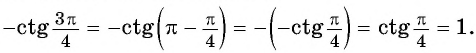
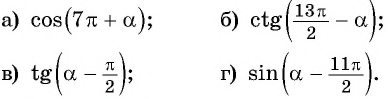
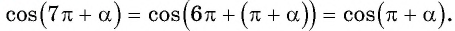
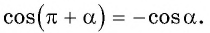
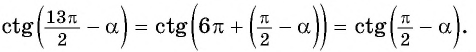
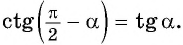
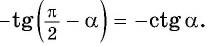
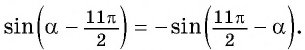
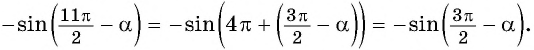
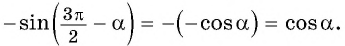
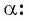

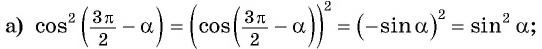
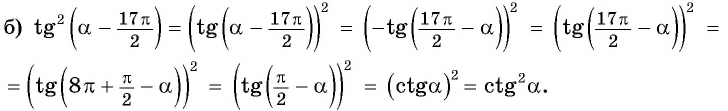

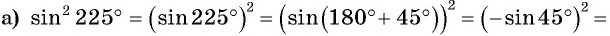
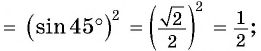
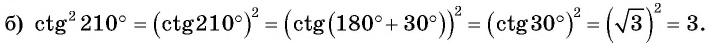
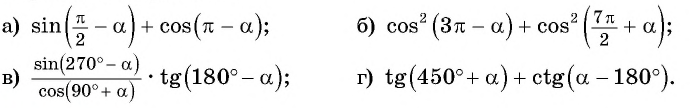
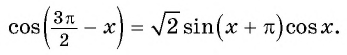
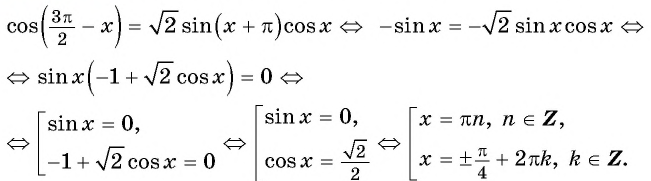
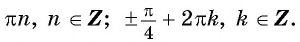








 выполняется через вертикальные «рабочие» углы
выполняется через вертикальные «рабочие» углы  название…. (функции меняется на конфункцию, синус на косинус, тангенс на котангенс и наоборот).
название…. (функции меняется на конфункцию, синус на косинус, тангенс на котангенс и наоборот).


